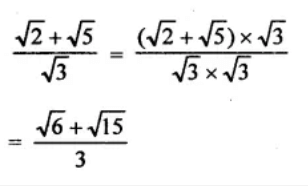01. Long Question Answers: Number System

Q1.Simplify the following expressions:

(i) (4 + √7) (3 + √2)
(ii) (√5 – √3)²
(iii) (√5 -2)( √3 – √5)

Sol. 

(i) (4 + √7) (3 + √2)

= 12 + 4√2 + 3√7 + √14

(ii)  (√5 – √3)²

= (√5)² + (√3)² – 2(√5)( √3)
= 5 + 3 – 2√15
= 8 – 2√15
(iii) (√5 -2)( √3 – √5)
= √15 – √25 – 2√3 + 2√5
= √15 – 5 – 2√3 + 2√5

Q2. Rationalise the denominator: (√2 + √5)/ √3

Sol. Multiply both the numerator and denominator with the same number to rationalise the denominator.

Q3. If ‘a’ and ‘b’ are rational numbers and,
then find the value of ‘a’ and ‘b’.

Sol.Rationalizing the fraction, we get

Now  

Equating a and b both sides
⇒ a + b√8 = 17 +6√8
⇒ a = 17and b = 6

Q4:Find five rational numbers between 3/5 and 4/5.

Sol:We have to find five rational numbers between 3/5 and 4/5.

So, let us write the given numbers by multiplying with 6/6, (here 6 = 5 + 1)

Now,

3/5 = (3/5) × (6/6) = 18/30

4/5 = (4/5) × (6/6) = 24/30

Thus, the required five rational numbers will be: 19/30, 20/30, 21/30, 22/30, 23/30

Q5: $\mathrm{Show}\mathrm{ that }0.3333\dots =0.3¯\mathrm{can}\mathrm{ be}\mathrm{ expressed}\mathrm{ in}\mathrm{ the }\mathrm{form}p/q,\mathrm{where}\mathrm{ p}\mathrm{ and}\mathrm{ q }\mathrm{are}\mathrm{ integers}\mathrm{ and}\mathrm{ q}\ne 0.$

Sol:

Let x = 0.3333…. 

Multiply with 10,

10x = 3.3333…

Now, 3.3333… = 3 + x (as we assumed x = 0.3333…)

Thus, 10x = 3 + x

10x – x = 3

9x = 3

x = 1/3

Therefore, 0.3333… = 1/3. Here, 1/3 is in the form of p/q and q ≠ 0.