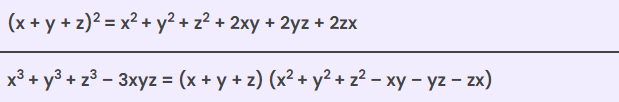02. Chapter Notes: Polynomials

by

Introduction 

Welcome to the intriguing world of polynomials! These mathematical expressions, made up of numbers and variables, are essential in algebra and help us model real-life situations. 

In this chapter, we’ll explore what polynomials are, their different types, and their significance. You’ll learn how to add, subtract, and multiply them, as well as how to factor them. 

Get ready to discover the power of polynomials and how they can enhance your understanding of mathematics!

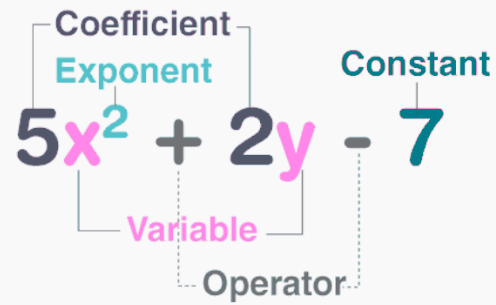
A polynomial is made up of one or more terms. Each term typically includes:

  • A coefficient (a numerical value),
  • A variable (like xx, yy, etc.),
  • And an exponent (a power of the variable).

For example, in the polynomial:

4x3 – 3x2 + 2x -5

  • The terms are 4x3 3x2 + 2x -5

Variable is denoted by a symbol that can take any real value, often represented by letters such as x, y, z, etc

 Coefficient:  the coefficient is simply the number that multiplies the variable in any given term of a polynomial. Each term of the polynomial has a coefficient.

Algebraic expressions are the mathematical equations consisting of variables, constants, terms and coefficients.

Expressions like 2x, 3x, -x, and -½ x are examples of algebraic expressions. Specifically in the form (a constant) x. When the constant is unknown, it is denoted as a, b, c, etc. 

Polynomial

A polynomial is an algebraic expression consisting of variables, coefficients, and exponents, combined using addition, subtraction, and multiplication operations.

  • Example:2�3−5�2+3�−72x3−5x 2+ 3x −7 is a polynomial.

“The expression which contains one or more terms with non – zero coefficient is called polynomial”

Understanding Expressions with Examples

  • Consider a square of side 3 units, where the perimeter is given by the sum of the lengths of its four sides. 
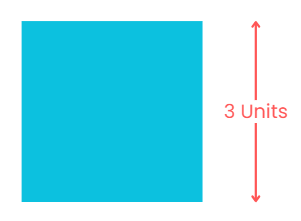
  • If each side is x units, the perimeter is expressed as 4x units, showcasing how the value of the variable influences the result. 
  • The area of the square, denoted as x² square units, is an example of an algebraic expression.

Try yourself:Which of the following is an example of a polynomial expression in one variable ?

  • A.2x + 3y
  • B.5xy – 7
  • C.3x2 + 2x – 5
  • D.x + 4 + y

Polynomials in One Variable

Polynomials are algebraic expressions with variables, coefficients, and exponents. When the exponents are whole numbers, the expressions are termed polynomials in one variable.

 Example: x³ – x² + 4x + 7 and 3y² + 5y.

Terms and Coefficients

In a polynomial like x² + 2x, x² and 2x are referred to as terms. Each term has a coefficient—in -x³ + 4x² + 7x – 2, coefficients are -1, 4, 7, and -2. The term x⁰ (where x⁰ = 1) is also present.

Constant Polynomials and Zero Polynomials

Constants like 2, -5, and 7 are examples of constant polynomials. The constant polynomial 0 is termed the zero polynomial, a significant concept in polynomial theory.

Non-Polynomial Expressions

Expressions like x + 2/x, x⁻¹, and x + 3√(x) aren’t polynomials due to non-whole number exponents.

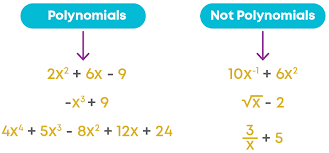
Notation for Polynomials

Polynomials can be denoted by symbols like p(x), q(x), or r(x), where the variable is x. Examples include:

  1. �(�)=2�2+5�−3p(x) = 2x 2+ 5x−3
  2. �(�)=�3−1q(x) = x 3−1
  3. �(�)=�3+�+1r(y) = y 3+ y + 1
  4. �(�)=2−�−�2+6�5s(u) = 2−u −u 2+ 6u 5

Degree of a Polynomial

The degree of a polynomial is the highest power of its variable. For example, in 3x⁷ – 4x⁶ + x + 9, the degree is 7. Constant polynomials have a degree of 0.

Examples:

 �(�)=�5−�4+3

Try yourself:

What is a polynomial?

  • A.An algebraic expression consisting of variables, coefficients, and exponents, combined using addition, subtraction, and multiplication operations.
  • B.An algebraic expression consisting of variables and constants, combined using addition, subtraction, and division operations.
  • C.An algebraic expression consisting of variables, coefficients, and exponents, combined using addition, subtraction, and division operations.
  • D.An algebraic expression consisting of variables and constants, combined using addition, subtraction, and multiplication operations.

Linear, Quadratic, and Cubic Polynomials

Linear Polynomial: Degree 1, written as ��+�ax+b where �≠0a is not equal to 0. 

Examples: 2�−12x−1, 2�+12y+1, 2−�2−u

Quadratic Polynomial: Degree 2, expressed as ��2+��+�ax2+bx+c where �≠0a is not equal to 0. 

Examples: 5−�25−y2, 4�+5�24y+5y2, 6−�−�26−y−y2

Cubic Polynomial: Degree 3, in the form ��3+��2+��+�ax3+bx2+cx+d where �≠0a is not equal to zero 0. 

Examples: 4�34x3, 2�3+12x3+1, 5�3+�25x3+x2  

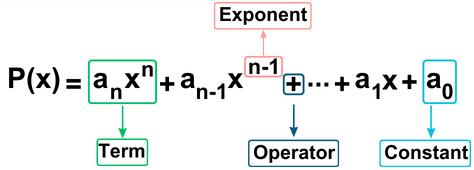
General Form of a Polynomial 

A polynomial in one variable x of degree n is an expression of the form 

Also read: Worksheet: Polynomials

Zero Polynomial and Beyond

The zero polynomial, denoted as 0, has an undefined degree. Polynomials can extend to more than one variable, 

like �2+�2+���x2+y2+xyz in three variables.

Zeroes of a Polynomial

Consider the polynomial �(�)=5�3−2�2+3�−2p(x)=5x3 − 2x2 + 3x −2. To find the value of �(�)p(x) at different points, we substitute the given values for �x. 

For Example,1) Given Polynomial: p(x) = 5x3 – 2x2 + 3x – 2

Calculation:

1. For x = 1:

   p(1) = 5 – 2 + 3 – 2 = 4

2. For x = 0:

   p(0) = 0 – 0 + 0 – 2 = -2

3. For x = -1:

   p(-1) = -5 – 2 – 3 – 2 = -12

In summary, for the given polynomial �(�)=5�3−2�2+3�−2p(x)=5x3−2x2+3x−2:

  • �(1)=4p(1)=4
  • �(0)=−2p(0)=−2
  • �(−1)=−12p(−1)=−12

These values are found by substituting the respective values of �x into the polynomial expression.

Example: Value of Polynomials at Given Points

(i) For �(�)=5�2−3�+7p(x)=5x2−3x+7 at �=1x=1: �(1)=5(1)2−3(1)+7=9p(1)=5(1)2−3(1)+7=9

(ii) For �(�)=3�3−4�+11q(y)=3y3−4y+11 at �=2y=2: �(2)=3(2)3−4(2)+11=27−8+11=30q(2)=3(2)3−4(2)+11=27−8+11=30

(iii) For �(�)=4�4+5�3−�2+6p(t)=4t4+5t3−t2+6 at �=�t=a: �(�)=4�4+5�3−�2+6p(a)=4a4+5a3−a2+6

Identifying Zeros of Polynomials

When evaluating �(�)=�−1p(x)=x−1 at �=1x=1, we find that �(1)=0p(1)=0. In general, if �(�)=0p(c)=0, we say that �c is a zero of the polynomial �(�)p(x). For example, for �(�)=�−1p(x)=x−1, �=1x=1 is a zero.

Zero Polynomial and Constant Polynomials

Constant polynomials like 55 have no zeros since replacing �x by any number in 5�05x0 still gives 55. The zero polynomial, denoted by 00, has every real number as its zero by convention.

Try yourself:What is the degree of the polynomial 3x4 – 2x2 + 5?

  • A.Degree 0
  • B.Degree 2
  • C.Degree 3
  • D.Degree 4

Factorization of Polynomials

Factor Theorem

If p(x) is a polynomial of degree �>1n>1 and �a is any real number, then (i) �−�x−a is a factor of �(�)p(x) if �(�)=0p(a)=0, and (ii) �(�)=0p(a)=0 if �−�x−a is a factor of �(�)p(x).

Proof: By the Remainder Theorem, �(�)=(�−�)�(�)+�(�)p(x)=(x−a)q(x)+p(a). 

(i) If �(�)=0p(a)=0, then �(�)=(�−�)�(�)p(x)=(x−a)q(x), showing that �−�x−a is a factor. 

(ii) Since �−�x−a is a factor of �(�)p(x), �(�)=(�−�)�(�)p(x)=(x−a)g(x) for some polynomial �(�)g(x). In this case, �(�)=(�−�)�(�)=0p(a)=(a−a)g(a)=0.

Example: Examining Factors

Examine whether �+2x+2 is a factor of �3+3�2+5�+6x3+3x2+5x+6 and of 2�+42x+4. Let �(�)=�3+3�2+5�+6p(x)=x3+3x2+5x+6 and �(�)=2�+4s(x)=2x+4.

Solution: For �(−2)p(−2): �(−2)=(−2)3+3(−2)2+5(−2)+6=0p(−2)=(−2)3+3(−2)2+5(−2)+6=0, so �+2x+2 is a factor.

For �(−2)s(−2): �(−2)=2(−2)+4=0s(−2)=2(−2)+4=0, so �+2x+2 is a factor.

In fact, 2�+4=2(�+2)2x+4=2(x+2), confirming the result without the Factor Theorem

Also read: Worksheet: Polynomials

Algebraic Identities

Algebraic identities are equations that hold true for all values of the variables involved. You may be familiar with several identities from earlier classes:

Identity I: (�+�)2=�2+2��+�2(x+y)2=x2+2xy+y2

Identity II: (�−�)2=�2−2��+�2(x−y)2=x2−2xy+y2

Identity III: �2−�2=(�+�)(�−�)x2−y2=(x+y)(x−y)

Identity IV: (�+�)(�+�)=�2+(�+�)�+��(x+a)(x+b)=x2+(a+b)x+ab

Example: Product Computation using Identities Problem

Find the following products using appropriate identities: 

(i) (x+2)(x+2) 

(ii)(x−4)(x+6)

Solution:

(i) For (�+2)(�+2)(x+2)(x+2), apply Identity I: (�+2)(�+2)=(�+2)2=�2+2(�)(2)+22=�2+4�+4(x+2)(x+2)=(x+2)2=x2+2(x)(2)+22=x2+4x+4

(ii) For (�−4)(�+6)(x−4)(x+6), use Identity IV: (�−4)(�+6)=�2+(−4+6)�+(−4)(6)=�2+2�−24(x−4)(x+6)=x2+(−4+6)x+(−4)(6)=x2+2x−24

Try yourself:Which of the following is not true about the polynomial x2 – 5x + 6?

  • A.The degree of the polynomial is 2.
  • B.The polynomial can be factored as (x – 3)(x – 2)
  • C.The polynomial has a zero at x = 3.
  • D.The constant term is -6..

Identity V : (x + y + z) 2 = x 2 + y 2 + z 2 + 2xy + 2yz + 2zx

Identity VI:

The identity (�+�)3=�3+�3+3��(�+�)(x+y)3=x3+y3+3xy(x+y) represents the cube of a binomial. 

Similarly, by replacing �y with −�−y, we get 

Identity VII: (�−�)3=�3−�3−3��(�−�)(x−y)3=x3−y3−3xy(x−y).

Example: Expanded Forms of Cubes

(i) For (2�+3�)3(2a+3b)3:

(2�+3�)3=8�3+27�3+36�2�+5(2a+3b)3=8a3+27b3+36a2b+54ab2

(ii) For (3�−2�)3(3x−2y)3:

(3�−2�)3=27�3−8�3−54�2�+36��2(3x−2y)3=27x3−8y3−54x2y+36xy2

Identity VIII:

The identity �3+�3+�3−3���=(�+�+�)(�2+�2+�2−��−��−��)x3+y3+z3−3xyz=(x+y+z)(x2+y2+z2−xy−yz−zx) expresses a factorization involving the sum and product of cubes.

Example: Factorization of 8�3+�3+27�3−18���8x3+y3+27z3−18xyz

Given the expression 8�3+�3+27�3−18���8x3+y3+27z3−18xyz, we can factorize it using Identity VIII:

8�3+�3+27�3−18���=(2�+�+3�)(4�2+�2+9�2−2��−3��−6��)8x3+y3+27z3−18xyz=(2x+y+3z)(4x2+y2+9z2−2xy−3yz−6xz)

Try yourself:Which of the following identities represents the cube of a binomial?

  • A.Identity VI
  • B.Identity IV
  • C.Identity VII
  • D.Identity VIII

Summary

1. Definition of a Polynomial:

A polynomial p(x) in one variable x is an algebraic expression written as,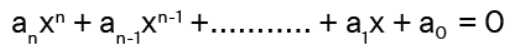
, where are constants and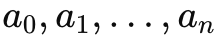and an
The term an is the leading coefficient and n is the degree of the polynomial.

2. Types of Polynomials:

  • Monomial: A polynomial with one term.
  • Binomial: A polynomial with two terms.
  • Trinomial: A polynomial with three terms.
  • Linear Polynomial: A polynomial of degree one.
  • Quadratic Polynomial: A polynomial of degree two.
  • Cubic Polynomial: A polynomial of degree three.

3. Zeros of Polynomials:

A real number a is a zero of a polynomial p(x) if p(a) = 0. Such a number is also called a root of the equation p(x) = 0.

4. Uniqueness and Existence of Zeros:

  • Every linear polynomial has a unique zero.
  • A non-zero constant polynomial has no zeros.
  • Every real number is a zero of the zero polynomial (polynomial where all coefficients are zero).

5. Factor Theorem:

x – a is a factor of the polynomial p(x) if p(a) = 0. Conversely, if x – a is a factor of p(x), then p(a) = 0.

6. Algebraic Identities:

  • For 2 variables (x and y) :
  • For 3 variables (x, y and z)