Multiple Choice Questions
Q1: If x/y + y/x = -1 and (xy, ≠ 0), the value of x3 – y3 is
(a) 1
(b) -1
(c) 0
(d) 2
Ans: (c)
x/y + y/x = -1
x2 + y2 = − xy
or
x2 + y2 + xy = 0
Now x3 – y3 = (x − y) (x2 + y2 + xy) = (x − y) × 0 = 0
Hence (c) is the correct answer
Q2: If p + q + r = 0 ,then the value of
(a) 1
(b) 3
(c) -1
(d) 0
Ans: (b)
Now we know that p3 + q3 + r3 − 3pqr = (p + q + r) (p2 + q2 + r2 − pq − qr − pr)
as p + q + r = 0
p3 + q3 + r3 − 3pqr = 0 or p3 + q3 + r3 = 3pqr
Now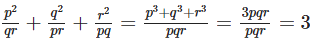
Hence (b) is the correct answer.
Q3: The product of (x + a) (x + b) is
(a) x2 + (a + b)x + ab
(b) x2 – (a – b)x + ab
(c) x2 + (a – b)x + ab
(d) x2 + (a – b)x + ab
Ans: (a)
(x+a) (x+b) = x(x+b) + a(x+b)
=x2 + bx + ax + ab
=x2 + (a+b)x + ab
Q4: The value of (x + 2y + 2z)2 + (x – 2y – 2z)2 is
(a) 2x2 + 8y2 + 8z2
(b) 2x2 + 8y2 + 8z2 + 8xyz
(c) 2x2 +8y2 + 8z2 – 8yz
(d) 2x2 + 8y2 + 8z2 + 16yz
Ans: (d)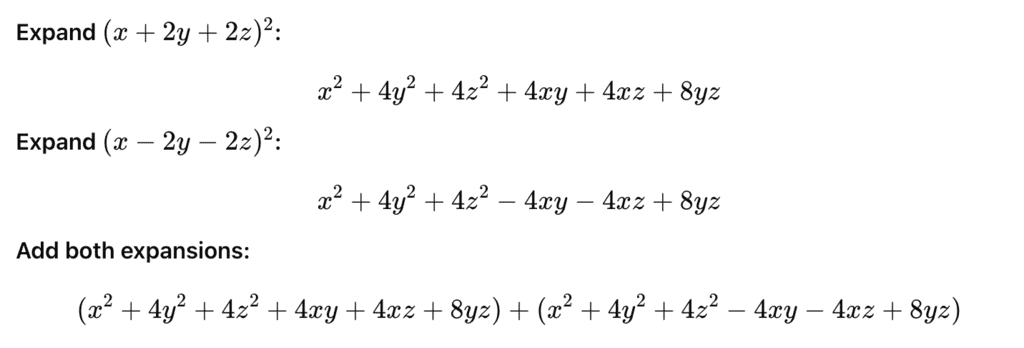
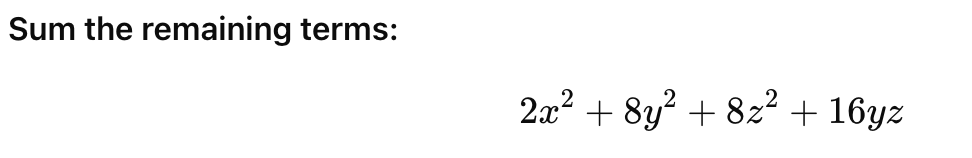
Q5: The value of f(x) = 5x−4×2+3 when x = -1, is:
(a) 3
(b) -12
(c) -6
(d) 6
Ans: (c)
To find the value of f(x) = 5x − 4x2+ 3 when x = −1, follow these steps:
Substitute x = −1 into the equation:
f (−1) = 5(−1) − 4(−1)2 + 3
f(−1) = −5 −4 + 3
f(−1) = −6
True or False
Q1: P(x) = x – 1 and g(x) =x2 – 2x + 1 . p(x) is a factor of g(x)
Ans: True, as g(1) = 0
Q2: The factor of 3x2 – x – 4 are (x + 1)(3x – 4)
Ans: True, we can get this by split method
Q3: Every linear polynomial has only one zero
Ans: True
Q4: Every real number is the zero’s of zero polynomial
Ans: True
Q5: A binomial may have degree 4
Ans: True, example x4 + 1
Q6: 0, 2 are the zeroes of x2– 2x
Ans: True
Q7: The degree of zero polynomial is not defined
Ans: True
Answer the following Questions
Q1: Is 3x1/2 – 4x + 15 a polynomial of one variable?
Ans: No. it is not a polynomial
Q2: Is ∛x – √2x a polynomial
Ans: No. It is not a polynomial
Q3: What will be the degree of polynomials 30x5 – 15x2 + 40
Ans: Degree of Polynomial is 5
Q4: Is (y2)1/2 + 2√3 a polynomial of one variable?
Ans: Yes it is a polynomial of one variable
Q5: What will be the coefficient of x3 in 9x3 – 5x + 20.
Ans: The coefficient of x3 is 9
Q6: Show that x = 1 is a root of the polynomial 3x3 – 4x2 + 8x – 7
Ans: On putting x = 1
X = 1 is root of polynomial
3x3 – 4x2 + 8x – 7
3(1)3 – 4(1)2 + 8(1) – 7
3 – 4 + 8 – 7 = 0
X = 1 is root of polynomial