Page No. 47
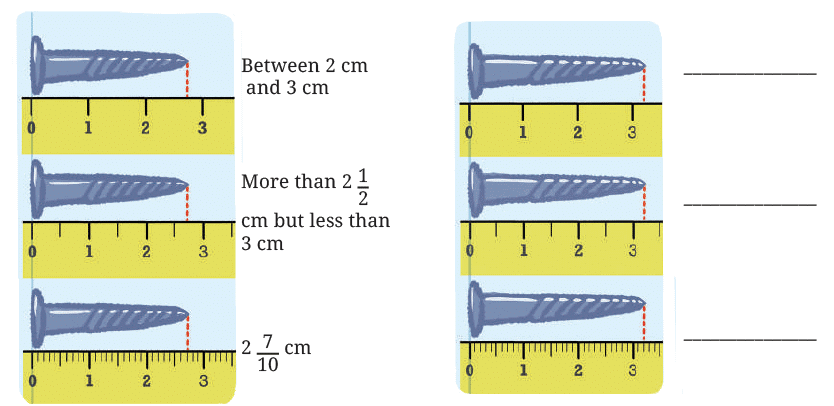
In the following figure, screws are placed above a scale. Measure them and write their length in the space provided.
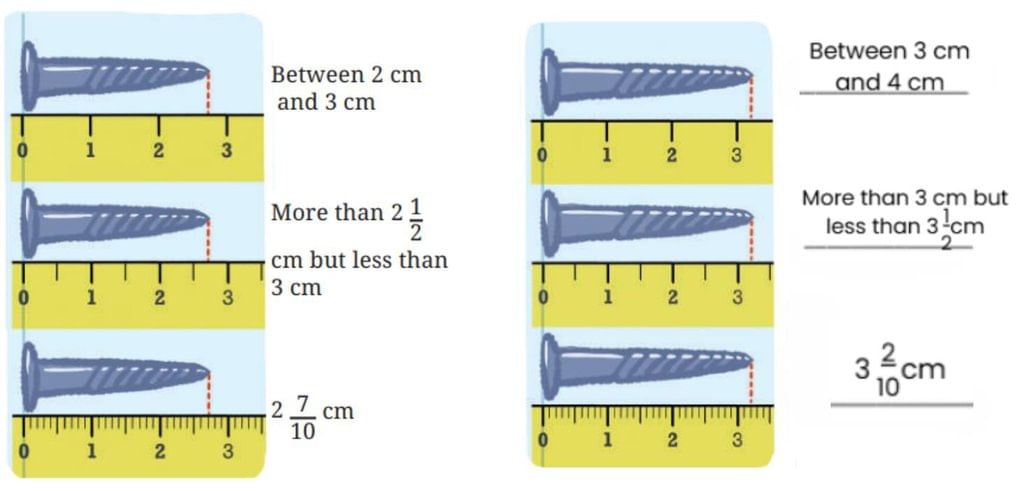
Ans:
Q1: Which scale helped you measure the length of the screws accurately? Why?
Ans: The scale that is divided into 10 equal parts between each centimeter mark helped measure the screws accurately. This is because it shows each tenth of a centimeter clearly, helping us measure the screw length precisely.
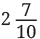
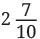
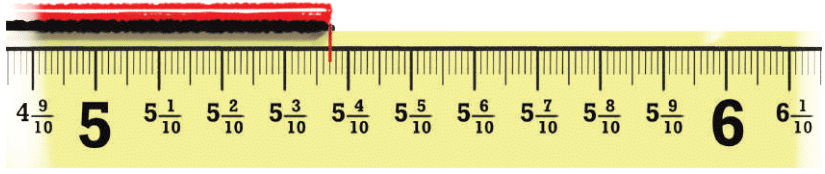
Q2: What is the meaning of cm (the length of the first screw)?
Ans: The number cm means that the screw is 2 centimeters and 7 parts out of 10 of another centimeter. The ruler is divided into 10 equal parts between each number. So, we count 2 full centimeters and then 7 small parts more. We read it as two and seven-tenth centimeters.
Q3: Can you explain why the unit was divided into smaller parts to measure the screws?
Ans: The unit was divided into smaller parts (tenths of a centimeter) to measure the screws because their lengths differed by a small amount, not detectable with whole centimeter markings. Smaller units allow for more precise measurements, capturing fine differences.
Q4: Measure the following objects using a scale and write their measurements in centimeters (as shown earlier for the lengths of the screws): pen, sharpener, and any other object of your choice.
Ans: (Measurements may vary depending on the actual objects; example answers below)
- Pen: 13.4 cm
- Sharpener: 3.2 cm
- Eraser: 4.7 cm
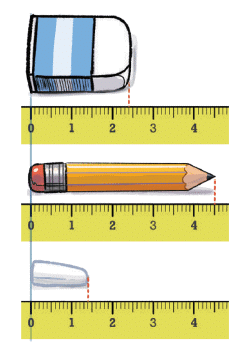
Q5: Write the measurements of the objects shown in the picture:
Ans: The picture, assuming typical objects:
- First Image Eraser: 2.4 cm
- Second Image Pencil: 4.5 cm
- Third Image Chalk: 1.4 cm
Page No. 49
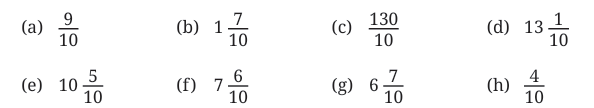
Q2: Arrange these lengths in increasing order:
Ans: We convert all the mixed numbers or improper fractions to decimal form:
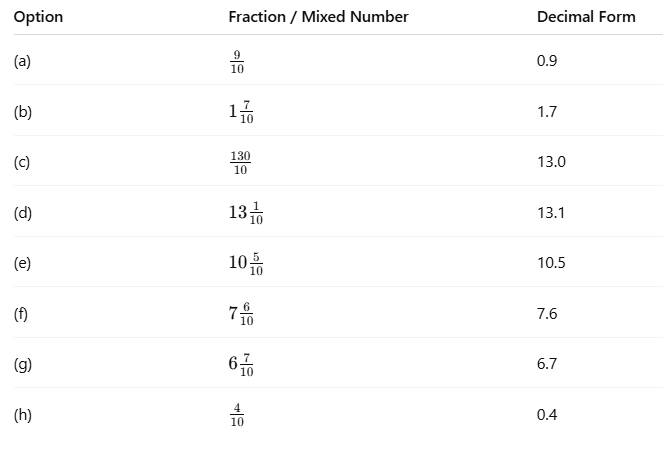
Arrange the decimals in increasing order
0.4 < 0.9 < 1.7 < 6.7 < 7.6 < 10.5 < 13.0 < 13.1
i.e., (h) < (a) < (b) < (g) < (f) < (e) < (c) < (d)
Page No. 50 & 51
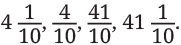
Q1: Arrange the following lengths in increasing order:
Ans: Let’s first convert all numbers into decimal form:
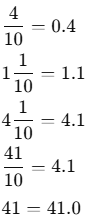
(b) < (a) = (c) < (d)
i.e.,
0.4 < 4.1 = 4.1 < 41.1
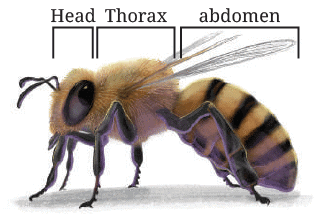
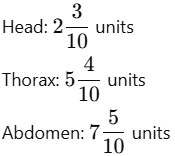
Q2: The lengths of the body parts of a honeybee are given. Find its total length.
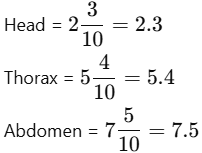
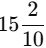
Ans: First, convert all mixed numbers into decimals or like fractions:
Now, add them: 2.3 + 5.4 + 7.5 = 15.2 units
Total length of the honeybee = 15.2 units or units
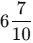
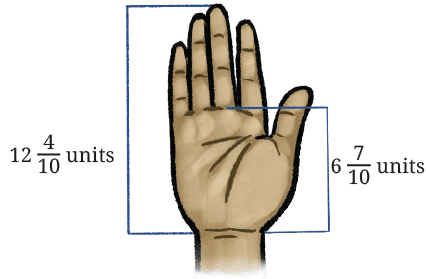
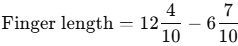
Q3: The length of Shylaja’s hand is units, and her palm is units. What is the length of the longest (middle) finger?
Ans: We subtract the length of the palm from the full hand to get the finger length:
Ans: Break the subtraction as:
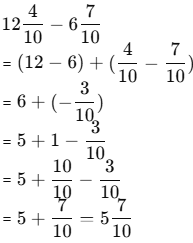
Since we cannot have a negative fraction, we adjust by borrowing 1 from the whole number (6).
Page No. 52
Q1: Try computing the difference by converting both lengths to tenths.
Ans: Convert the mixed number to improper fraction:
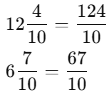
Now subtract:
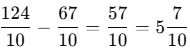
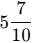
So, the length of the finger isunits.
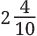
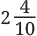
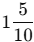
Q2: A Celestial Pearl Danio’s length is cm, and the length of a Philippine Goby is 9/10 cm. What is the difference in their lengths?
Ans: First, convert the mixed number to decimal:
Celestial Pearl Danio = = 2.4 cm
Philippine Goby = 9/10 = 0.9 cm
Now, subtract: Difference = 2.4 − 0.9 = 1.5 cm
So, the difference in their lengths is 1.5 cm or cm.
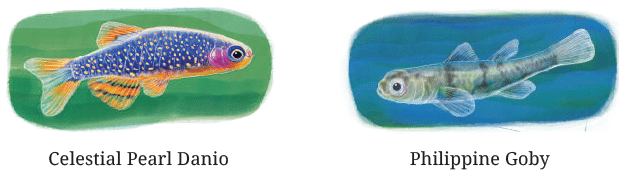
Q2: How big are these fish compared to your finger?
Ans: The Celestial Pearl Danio is about the size of an average adult finger, around 2-2.5 cm long.
The Philippine Goby is slightly smaller, about half the length of an average finger, around 1-1.5 cm long.
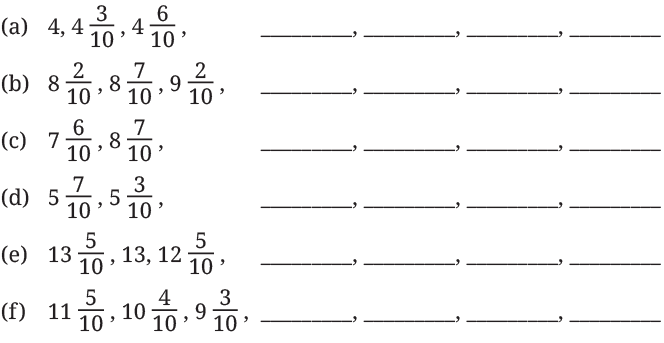
Q3: Observe the given sequences of numbers. Identify the change after each term and extend the pattern:
Ans:
Page No. 53
Q: How many one-hundredths make one-tenth? Can we also say that the length is 4 units and 45 one-hundredths?
Ans: Yes, we can say that.
If a length is written as 4.45 units, it means 4 whole units and 45 hundredths (or 45100) of a unit.
So, “4 units and 45 one-hundredths” is another way of saying 4.45 units.
Page No. 54
Q1: Observe the figure below. Notice the markings and the corresponding lengths written in the boxes when measured from 0. Fill the lengths in the empty boxes.
Ans:
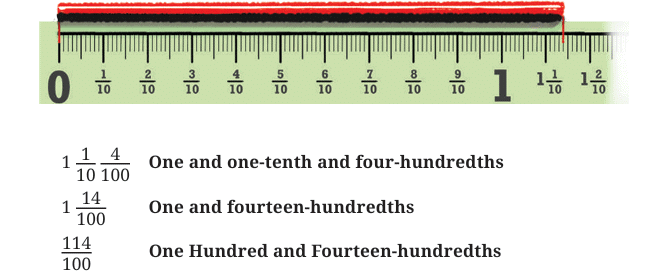
The length of the wire in the first picture is given in three different ways. Can you see how they denote the same length?
Ans:
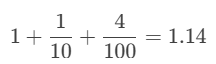One and one-tenth and four-hundredths”:
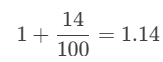“One and fourteen-hundredths”:
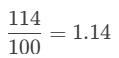“One Hundred and Fourteen-hundredths”:
Q2: For the lengths shown below write the measurements and read out the measures in words.
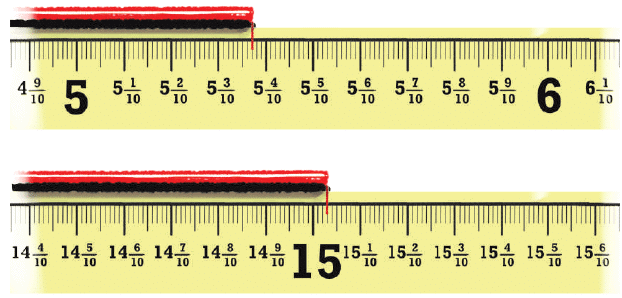
Ans: First Image:⁵³⁄₁₀₀ = ⁵³⁄₁₀₀
Five and three-tenths and seven-hundredths
Or ⁵³⁄₁₀₀
Five and thirty-seven-hundredths
Or ⁵³⁷⁄₁₀₀₀
Five hundred thirty-seven-hundredths
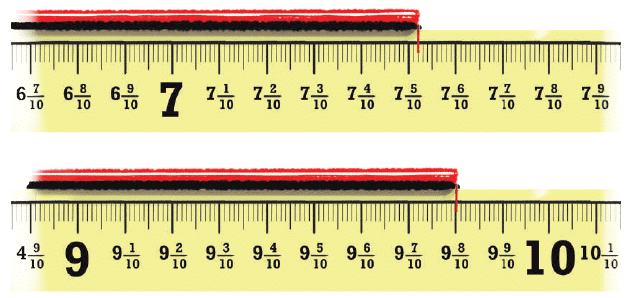
Second Image: 15³⁄₁₀₀
Fifteen and three-hundredths
Or ¹⁵⁰³⁄₁₀₀
One thousand five hundred three-hundredths
Third Image:
7⁵²⁄₁₀₀
Seven and five-tenths and two-hundredths
Or 7⁵²⁄₁₀₀
Seven and fifty-two-hundredths
Or ⁷⁵²⁄₁₀₀
Seven hundred fifty-two-hundredths
Fourth Image:
⁹⁸⁄₁₀
Nine and eight-tenths
Or ⁹⁸⁄₁₀₀
Nine and eighty-hundredths
Or ⁹⁸⁰⁄₁₀₀
Nine hundred eighty-hundredths
Page No. 55
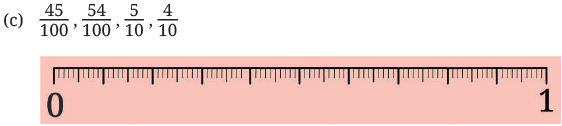
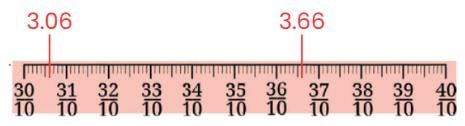
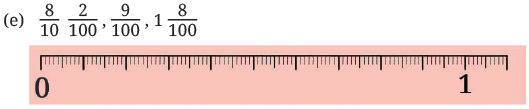
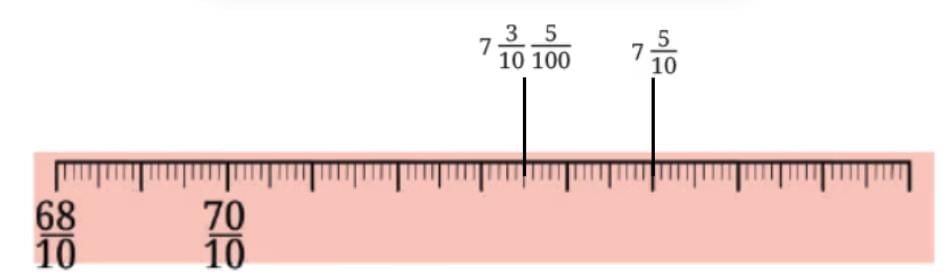
Q1: In each group, identify the longest and the shortest lengths. Mark each length on the scale.
Ans:
Ans:
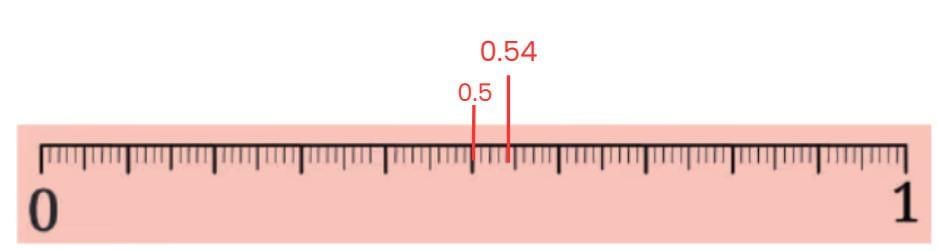
Ans:
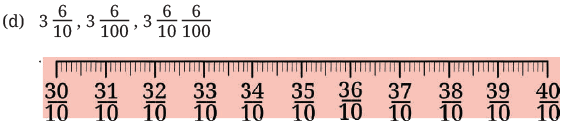
Ans:
Ans: Longest:
Shortest:
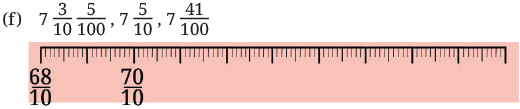
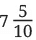
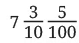
Ans: Longest:
Shortest:
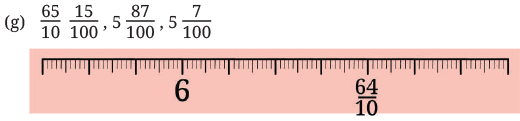
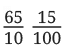
Ans: Longest:
Shortest:
Page 56 & 57
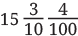
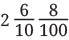
Q1: What will be the sum of and ?
Ans: We add the whole numbers, tenths, and hundredths separately.
Whole numbers: 15 + 2 = 17
Tenths: 3/10 + 6/10 = 9/10
Hundredths: 4/100 + 8/100 = 12/100
Now, convert and combine:
12/100 = 1/10 + 2/100
Add 9/10 + 1/10 = 1
Now the total is:
- Whole numbers: 17 + 1 = 18
- Tenths and hundredths left: 2/100
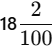
Final Answer:
Q2: Are both these methods different?
Ans: No, both Method 1 and Method 2 are not different in result. They are just two different ways of adding the same numbers.
- Method 1 adds the whole numbers, tenths, and hundredths separately using brackets and regrouping.
- Method 2 aligns the numbers in columns and adds them directly like we do in usual addition.
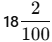
In both methods, the final answer is the same:
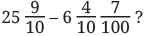
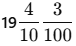
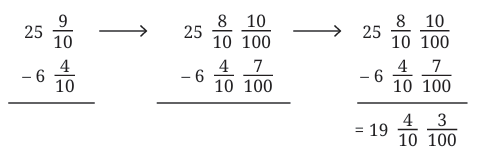
Q3: What is the difference:
Ans: We subtract the whole numbers, tenths, and hundredths step by step.
Whole numbers: 25 − 6 = 19
Tenths: 9/10 − 4/10 = 5/10
Hundredths: Since the first number has 0 hundredths, and we subtract 7/100, we need to convert 1/10 = 10/100
So, we take 9/10 = 8/10 + 1/10 = 8/10 + 10/100
Now subtract:
10/100 − 7/100 = 3/100
So the total is:
Whole: 19
Tenths: 4/10
Hundredths: 3/100
Final Answer:
Page No. 58
Figure it Out
Q1: Find the sums and differences:
(a) ³⁄₁₀ + ³⁴⁄₁₀₀
³⁄₁₀ + ³⁴⁄₁₀₀ = ³⁄₁₀ + ³⁴⁄₁₀₀
= 3 + ³⁄₁₀ + ⁴⁄₁₀₀ = 3 + ³⁴⁄₁₀₀ = ³³⁴⁄₁₀₀
(b) 9⁵⁷⁄₁₀₀ + 2¹³⁄₁₀₀
9⁵⁷⁄₁₀₀ + 2¹³⁄₁₀₀
= (9 + 2) + (⁵⁄₁₀ + ¹⁄₁₀) + (⁷⁄₁₀₀ + ³⁄₁₀₀)
= 11 + ⁶⁄₁₀ + ¹⁰⁄₁₀₀
= 11 + ⁶⁄₁₀ + ¹⁄₁₀ = 11⁷⁄₁₀
(c) 15⁶⁴⁄₁₀₀ + 14³⁶⁄₁₀₀
15⁶⁴⁄₁₀₀ + 14³⁶⁄₁₀₀
= (15 + 14) + (⁶⁄₁₀ + ³⁄₁₀) + (⁴⁄₁₀₀ + ⁶⁄₁₀₀)
= 29 + ⁹⁄₁₀ + ¹⁰⁄₁₀₀
= 29 + ⁹⁄₁₀ + ¹⁄₁₀ = 29 + ¹⁰⁄₁₀
= 29 + 1 = 30
(d) ⁷⁷⁄₁₀₀ − ⁴⁴⁄₁₀₀
⁷⁷⁄₁₀₀ − ⁴⁴⁄₁₀₀
= ³³⁄₁₀₀
(e) ⁸⁶⁄₁₀₀ − ⁵³⁄₁₀₀
⁸⁶⁄₁₀₀ − ⁵³⁄₁₀₀ = (8 − 5) + (⁶⁄₁₀₀ − ³⁄₁₀₀) = ³³⁄₁₀₀
(f) ¹²⁶²⁄₁₀₀ − ⁹⁹⁄₁₀₀
¹²⁶²⁄₁₀₀ → ¹²⁵⁄₁₀₀ → ¹¹¹⁵⁄₁₀₀ − ⁹⁹⁄₁₀₀ − ⁹⁹⁄₁₀₀ − ⁹⁹⁄₁₀₀
= ¹¹⁶³⁄₁₀₀ = ¹¹⁶³⁄₁₀₀
Page No. 59
Q1: Can we not split a unit into 4 equal parts, 5 equal parts, 8 equal parts, or any other number of equal parts instead?
Ans: Yes, a unit can be split into any number of equal parts (e.g., 4, 5, 8) for measurement.
For example, splitting into 4 parts gives quarters (1/4), and each quarter can be further divided into 4 for sixteenths (1/16).
Q2: Then why split a unit into 10 parts every time?
Ans: Splitting into 10 parts aligns with the Indian place value system, where each place value is 10 times the next (e.g., 10 ones = 1 ten).
This consistency extends to fractions (10 tenths = 1 unit, 10 hundredths = 1 tenth), making decimal notation and calculations simpler.
Page No. 60
Q1: Can we extend this further?
Ans: Yes, the place value system extends beyond thousandths. Splitting 1/1000 into 10 parts gives 1/10000 (ten-thousandths), and so on, allowing for increasingly precise measurements.
Page No. 61
Q1: We can ask similar questions about fractional parts:
(a) How many thousandths make one unit?
(b) How many thousandths make one tenth?
(c) How many thousandths make one hundredth?
(d) How many tenths make one ten?
(e) How many hundredths make one ten?
Ans: (a) 1000 thousandths make one unit (1 = 1000/1000).
(b) 100 thousandths make one tenth (1/10 = 100/1000).
(c) 10 thousandths make one hundredth (1/100 = 10/1000).
(d) 100 tenths make one ten (10 = 100/10).
(e) 1000 hundredths make one ten (10 = 1000/100).
Q2: Make a few more questions of this kind and answer them.
Ans:
(a) How many tenths make one hundred?
10001000 tenths (0.1×1000=1000.1×1000=100).
(b) How many units make one thousand?
10001000 units (1×1000=10001×1000=1000).
(c) How many tenths make one unit?
10 tenths (0.1×10=10.1×10=1).
(d) How many hundredths make one thousand?
100,000100,000 hundredths (0.01×100,000=10000.01×100,000=1000).
Page No. 64
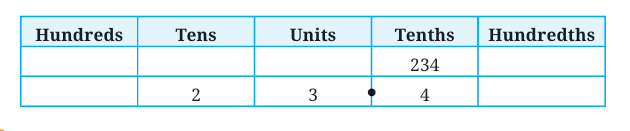
Q1: How can we write 234 tenths in decimal form?
Ans: 234 tenths = 234/10 = 23 4/10 = 23.4.
Q2: Write these quantities in decimal form:
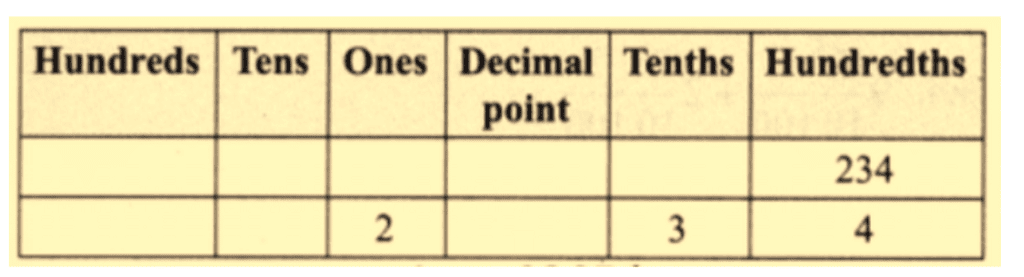
(a) 234 hundredths,
Ans: 234 hundredths means 234/100.
So, the decimal form is 2.34
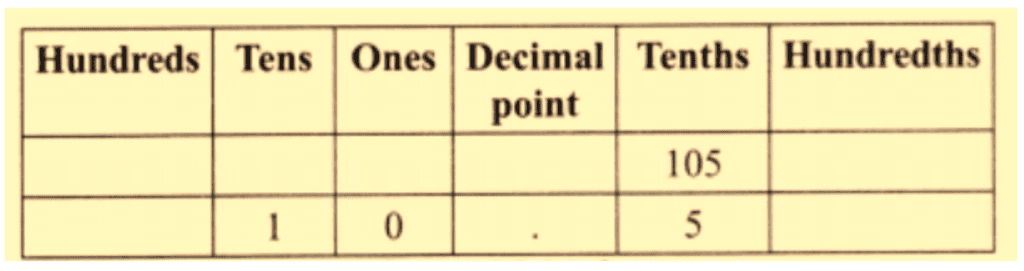
(b) 105 tenths.
Ans: 105 tenths means 105/10.
So, the decimal form is 10.5
Q3: How many cm is 1 mm?
Ans: 1 mm = 1/10 cm = 0.1 cm.
Q4: How many cm is (a) 5 mm? (b) 12 mm?
Ans: (a) 5 mm = 5/10 cm = 0.5 cm.
(b) 12 mm = 1 cm + 2/10 cm = 1.2 cm.
Page No. 65
Q1: Fill in the blanks below (mm ↔ cm):
Ans:
Page No. 66
Q1: Fill in the blanks below (cm ↔ m):
Ans:
Q2: How many mm does 1 meter have?
Ans: 1 m = 100 cm = 100 × 10 mm = 1000 mm.
Q3: Can we write 1 mm = 1/1000 m?
Ans: Yes, 1 mm = 1/1000 m, since 1 m = 1000 mm.
Page No. 67 & 68
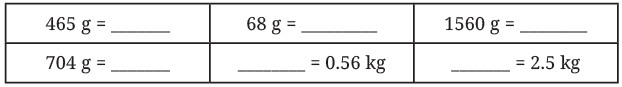
Q: Fill in the blanks below (g ↔ kg)
Ans:
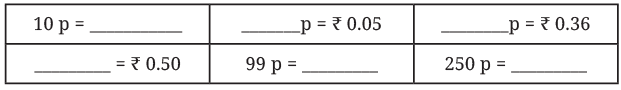
Q: Fill in the blanks below (rupee ↔ paise)
Ans:
Page No. 70 & 71
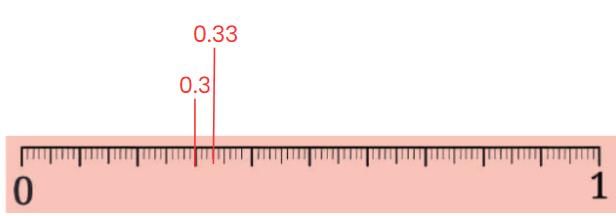
Q1: Name all the divisions between 1 and 1.1 on the number line.
Ans: The divisions between 1 and 1.1 are: 1.01, 1.02, 1.03, 1.04, 1.05, 1.06, 1.07, 1.08, 1.09
Q2: Identify and write the decimal numbers against the letters.
Ans: A = 5.09
B = 5.13
C = 5.20
D = 5.31
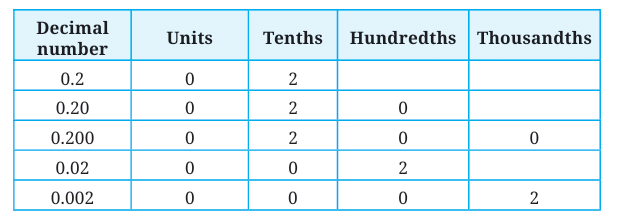
Q3: Sonu says that 0.2 can also be written as 0.20, 0.200; Zara thinks that putting zeros on the right side may alter the value of the decimal number. What do you think?
Ans: Sonu is correct. 0.2 = 0.20 = 0.200, as trailing zeros after the decimal point do not change the value (they represent 0 hundredths, 0 thousandths, etc.). Zara is incorrect.
We can see that 0.2, 0.20, and 0.200 are all equal as they represent the same quantity, i.e., 2 tenths. But 0.2, 0.02, and 0.002 are different.
Q4: Can you tell which of these is the smallest and which is the largest?
Ans: From the table above: 0.2 = 0.20 = 0.200 (same), 0.02, 0.002.
Smallest: 0.002, Largest: 0.2.
Q5: Which of these are the same: 4.5, 4.05, 0.405, 4.050, 4.50, 4.005, 04.50?
Ans: 4.5 = 4.50 = 04.50 (trailing zeros).
Others (4.05, 0.405, 4.050, 4.005) are distinct.
Same: 4.5, 4.50, 04.50.
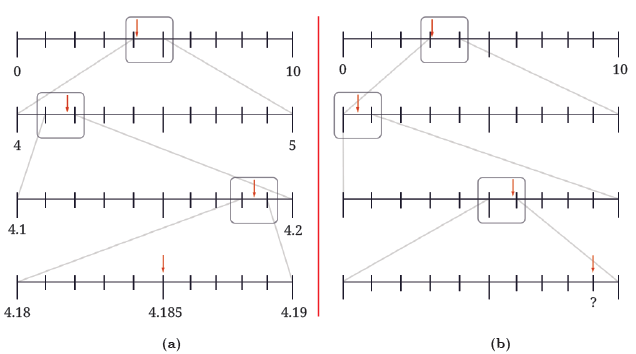
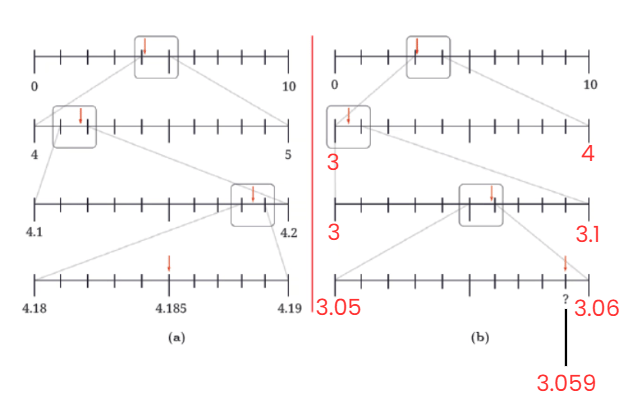
Q6: (a) Observe the number lines in Figure (a) below. At each level, a particular segment of the number line is magnified to locate the number 4.185.
(b) Identify the decimal number in the last number line in Figure (b) denoted by ‘?’.
Ans: Q7: Make such number lines for the decimal numbers: (a) 9.876 (b) 0.407.
Ans: (a) 9.876:
Number line from 9 to 10, divide into 10 parts (tenths: 9.8, 9.9), then 9.8 to 9.9 into 10 parts (hundredths: 9.87, 9.88), then 9.87 to 9.88 into 10 parts (thousandths: 9.876).
Draw a number line on your own.
(b) 0.407:
Number line from 0 to 1, divide into 10 parts (tenths: 0.4, 0.5), then 0.4 to 0.5 into 10 parts (hundredths: 0.40, 0.41), then 0.40 to 0.41 into 10 parts (thousandths: 0.407).
Draw a number line on your own.
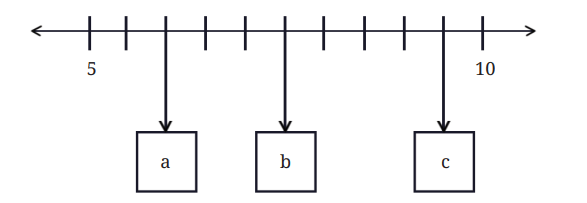
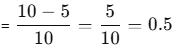
Q8: In the number line shown below, what decimal numbers do the boxes labelled ‘a’, ‘b’, and ‘c’ denote?
Ans: We are given that the number line from 5 to 10 is divided into 10 equal parts.
So, each small division
- a = 6
- b = 7.5
- c = 9.5
Page No. 72
Q1: Using similar reasoning find out the decimal numbers in the boxes below.
Ans: (Assuming similar scale, 5 to 10, 10 divisions):
- d = 8.01
- e = 8.05
- f = 4.35
- g = 4.5
- h = 4.85
Q2: Which is larger: 6.456 or 6.465?
Ans: Compare digits:
- Units: 6 = 6.
- Tenths: 4 = 4.
- Hundredths: 5 = 6 (stop here, 6 > 5).
6.465 is larger.
Page No. 73
Q1: Why can we stop comparing at this point? Can we be sure that whatever digits are there after this will not affect our conclusion?
Ans: We stop when digits differ because subsequent digits represent smaller place values (thousandths, etc.), which cannot overturn the difference in a higher place value (hundredths in this case). Thus, 6.465 > 6.456 regardless of further digits.
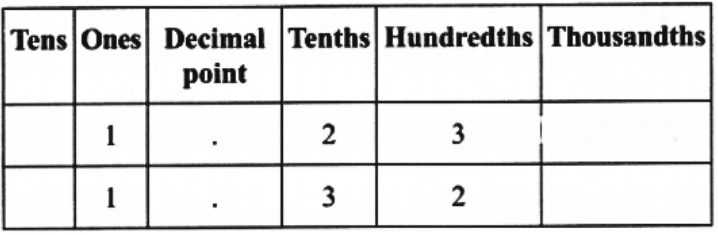
Q2: Which decimal number is greater?
(a) 1.23 or 1.32
(b) 3.81 or 13.800
(c) 1.009 or 1.090
Ans: (a) Using the decimal place value chart, we find that:
Both numbers have 1 unit, but the first number has 2 tenths, whereas the second number has 3 tenths.
Therefore, 1.23 < 1.32.
(b) Using the decimal place value chart, we find that:
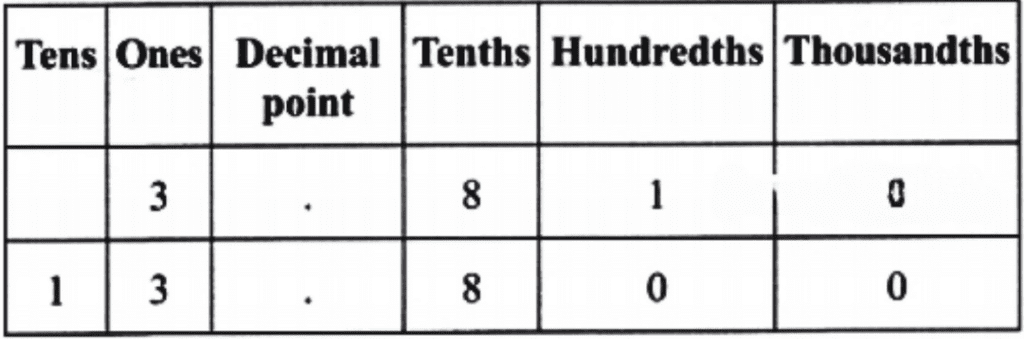
Here, the first number has 3 units, whereas the second number has 1 ten and 3 units.
Therefore, 3.81 < 13.800.
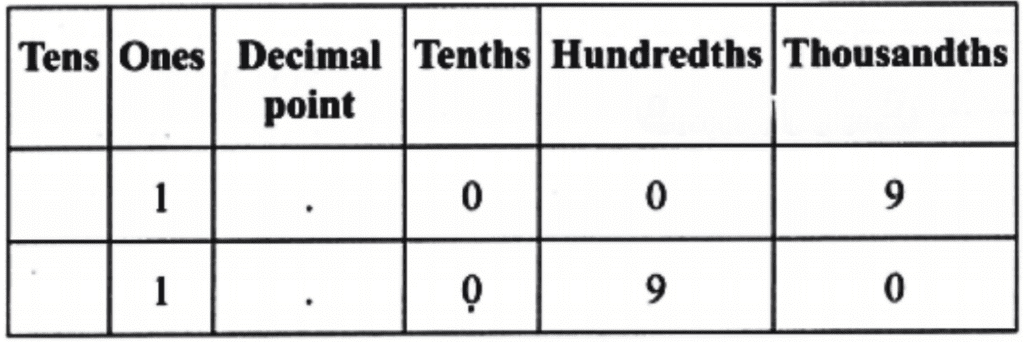
(c) Using the decimal place value chart, we find that:
Both numbers have 1 unit and 0 tenths, but the first number has 0 hundredths, whereas the second number has 9 hundredths.
Therefore, 1.009 < 1.090.
Q3: Consider the decimal numbers 0.9, 1.1, 1.01, and 1.11. Identify the decimal number that is closest to 1. Let us compare the decimal numbers. Arranging these in ascending order, we get 0.9 < 1 < 1.01 < 1.1 < 1.11. Among the neighbours of 1, 1.01 is 1/100 away from 1 whereas 0.9 is 10/100 away from 1. Therefore, 1.01 is closest to 1.
Which of the above is closest to 1.09?
Ans: From 0.9, 1.1, 1.01, 1.11:
- |1.09 − 0.9| = 0.19
- |1.09 − 1.1| = 0.01
- |1.09 − 1.01| = 0.08
- |1.09 − 1.11| = 0.02
Closest: 1.1.
Q4: Which among these is closest to 4: 3.56, 3.65, 3.099?
Ans:
- |4 − 3.56| = 0.44
- |4 − 3.65| = 0.35
- |4 − 3.099| = 0.901
Closest: 3.65.
Q5: Which among these is closest to 1: 0.8, 0.69, 1.08?
Ans:
- |1 − 0.8| = 0.2
- |1 − 0.69| = 0.31
- |1 − 1.08| = 0.08
Closest: 1.08.
Q6: In each case below use the digits 4, 1, 8, 2, and 5 exactly once and try to make a decimal number as close as possible to 25.
Ans: We can make a decimal number closest to 25 using the digits 4, 1, 8, 2, and 5 with the given conditions as follows:
Page No. 75
Q1: Write the detailed place value computation for 84.691 − 77.345, and its compact form.
Ans: Break the numbers into place values:
84.691
- Tens = 80
- Units = 4
- Tenths = 0.6
- Hundredths = 0.09
- Thousandths = 0.001
77.345
- Tens = 70
- Units = 7
- Tenths = 0.3
- Hundredths = 0.04
- Thousandths = 0.005
Now subtract each place value:
- Tens: 80 − 70 = 10
- Units: 4 − 7 = −3, borrow 1 from tens → 10 − 1 = 9, units become 14 − 7 = 7
- Tenths: 0.6 − 0.3 = 0.3
- Hundredths: 0.09 − 0.04 = 0.05
- Thousandths: 0.001 − 0.005 = Not possible → borrow from hundredths:
- 0.09 = 0.08 + 0.01
- 0.01 − 0.005 = 0.005
- So final hundredths = 0.08 − 0.04 = 0.04
- Thousandths = 0.005 − 0 = 0.005
Now combine all: Difference = 7.346
Compact Form: 84.691−77.345 = 7.346
Figure it Out
Q1: Find the sums:
(a) 5.3 + 2.6
(b) 18 + 8.8
(c) 2.15 + 5.26
(d) 9.01 + 9.10
(e) 29.19 + 9.91
(f ) 0.934 + 0.6
(g) 0.75 + 0.03
(h) 6.236 + 0.487
Ans:
(a) 5.3 + 2.6 = 7.9
(b) 18 + 8.8 = 26.8
(c) 2.15 + 5.26 = 7.41
(d) 9.01 + 9.10 = 18.11
(e) 29.19 + 9.91 = 39.10
(f) 0.934 + 0.6 = 1.534
(g) 0.75 + 0.03 = 0.78
(h) 6.236 + 0.487 = 6.723
Q2: Find the differences:
(a) 5.6 – 2.3
(b) 18 – 8.8
(c) 10.4 – 4.5
(d) 17 – 16.198
(e) 17 – 0.05
(f) 34.505 – 18.1
(g) 9.9 – 9.09
(h) 6.236 – 0.487
Ans:
(a) 5.6 − 2.3 = 3.3
(b) 18 − 8.8 = 9.2
(c) 10.4 − 4.5 = 5.9
(d) 17 − 16.198 = 0.802
(e) 17 − 0.05 = 16.95
(f) 34.505 − 18.1 = 16.405
(g) 9.9 − 9.09 = 0.81
(h) 6.236 − 0.487 = 5.749
Q3: Continue this sequence and write the next 3 terms: 4.4, 4.8, 5.2, 5.6, 6.0.
Ans: Change: +0.4.
Next: 6.4, 6.8, 7.2.
Page No. 76
Q1: Similarly, identify the change and write the next 3 terms for each sequence given below. Try to do this computation mentally.
(a) 4.4, 4.45, 4.5, …
(b) 25.75, 26.25, 26.75, …
(c) 10.56, 10.67, 10.78, …
(d) 13.5, 16, 18.5, …
(e) 8.5, 9.4, 10.3, …
(f) 5, 4.95, 4.90, …
(g) 12.45, 11.95, 11.45, …
(h) 36.5, 33, 29.5, …
Ans:
(a) 4.4, 4.45, 4.5: +0.05.
Next: 4.55, 4.60, 4.65.
(b) 25.75, 26.25, 26.75: +0.50.
Next: 27.25, 27.75, 28.25.
(c) 10.56, 10.67, 10.78: +0.11.
Next: 10.89, 11.00, 11.11.
(d) 13.5, 16, 18.5: +2.5.
Next: 21.0, 23.5, 26.0.
(e) 8.5, 9.4, 10.3: +0.9.
Next: 11.2, 12.1, 13.0.
(f) 5, 4.95, 4.90: −0.05.
Next: 4.85, 4.80, 4.75.
(g) 12.45, 11.95, 11.45: −0.50.
Next: 10.95, 10.45, 9.95.
(h) 36.5, 33, 29.5: −3.5.
Next: 26.0, 22.5, 19.0.
Q2: Make your own sequences and challenge your classmates to extend the pattern.
Ans: Example: 2.3, 2.9, 3.6 (+0.6, +0.7, increasing by 0.1).
Next: 4.4, 5.3, 6.4.
Estimating Sums and Differences
Sonu has observed sums and differences of decimal numbers and says, “If we add two decimal numbers, then the sum will always be greater than the sum of their whole number parts. Also, the sum will always be less than 2 more than the sum of their whole number parts.” Let us use an example to understand what his claim means:
If the two numbers to be added are 25.936 and 8.202, the claim is that their sum will be greater than 25 + 8 (whole number parts) and will be less than 25 + 1 + 8 + 1.
Q3: What do you think about this claim? Verify if this is true for these numbers. Will it work for any 2 decimal numbers?
Ans: Sonu’s claim: Sum of decimals > sum of whole parts, < sum of whole parts + 2.
For 25.936 + 8.202 = 34.138:
- Whole parts: 25 + 8 = 33 < 34.138.
- Whole parts + 2: 33 + 2 = 35 > 34.138.
True for this case. Generally true, as fractional parts add to less than 2 units.
Q4: What about for the sum of 25.93603259 and 8.202?
Ans: 25.93603259 + 8.202 = 34.13803259.
- 25 + 8 = 33 < 34.13803259.
- 33 + 2 = 35 > 34.13803259.
Claim holds.
Q5: Similarly, come up with a way to narrow down the range of whole numbers within which the difference of two decimal numbers will lie.
Ans: Numbers:
25.936 and 8.202
Step 1: Whole number parts:
25 − 8 = 17
Step 2: Full decimal subtraction:
25.936 − 8.202 = 17.734
So the difference:
- Is less than 25 − 8 + 1 = 18
- Is more than 25 − (8 + 1) = 16
So we can say:
“The difference will always lie between (Whole1 − Whole2 − 1) and (Whole1 − Whole2 + 1)”
For example:
If Whole parts are 25 and 8
→ Range of difference = Between 16 and 18
→ Actual difference = 17.734 lies in the range.
Page No. 78
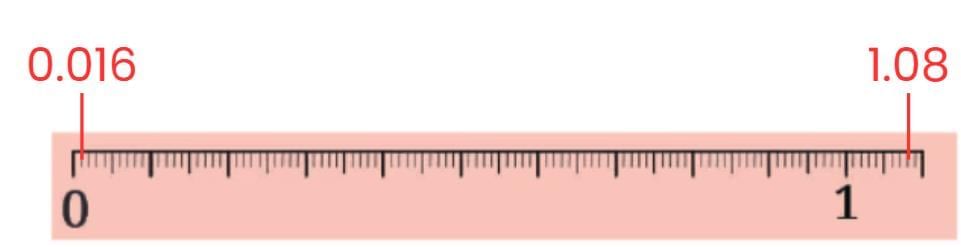
Q1: Where else can we see such ‘non-decimals’ with a decimal-like notation?
Ans: Examples:
- Time: 2.5 hours = 2 hours 30 minutes (not 2 hours 5 minutes).
- Money: ₹10.5 = 10 rupees 50 paise (not 10 rupees 5 paise).
- Sports: 5.5 overs = 5 overs 3 balls (1 over = 6 balls).
Q2: Convert the following fractions into decimals:
(a) 5/100
(b) 16/1000
(c) 12/10
(d) 254/1000
Ans:
(a) 5/100 = 0.05
(b) 16/1000 = 0.016
(c) 12/10 = 1.2
(d) 254/1000 = 0.254
Page no. 79
Q: Convert the following decimals into a sum of tenths, hundredths, and thousandths:
(a) 0.34
(b) 1.02
(c) 0.8
(d) 0.362
Ans: (a) 0.34 = ³⁴⁄₁₀₀ = ³⁰⁄₁₀₀ + ⁴⁄₁₀₀ = ³⁄₁₀ + ⁴⁄₁₀₀
(b) 1.02 = ¹⁰²⁄₁₀₀ = ¹⁰⁰⁄₁₀₀ + ²⁄₁₀₀
(c) 0.8 = ⁸⁄₁₀
(d) 0.362 = ³⁶²⁄₁₀₀₀ = ³⁰⁰⁄₁₀₀₀ + ⁶⁰⁄₁₀₀₀ + ²⁄₁₀₀₀
= ³⁄₁₀ + ⁶⁄₁₀₀ + ²⁄₁₀₀₀
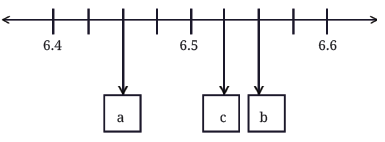
Q: What decimal number does each letter represent in the number line below?
Ans: (Here divisions of 0.025):
- a: 6.45
- b: 6.55
- c: 6.525
Q: Arrange the following quantities in descending order:
(a) 11.01, 1.011, 1.101, 11.10, 1.01
(b) 2.567, 2.675, 2.768, 2.499, 2.698
(c) 4.678 g, 4.595 g, 4.600 g, 4.656 g, 4.666 g
(d) 33.13 m, 33.31 m, 33.133 m, 33.331 m, 33.313 m
Ans: (a) 11.01, 1.011, 1.101, 11.10, 1.01: 11.10, 11.01, 1.101, 1.011, 1.01.
(b) 2.567, 2.675, 2.768, 2.499, 2.698: 2.768, 2.698, 2.675, 2.567, 2.499.
(c) 4.678 g, 4.595 g, 4.600 g, 4.656 g, 4.666 g: 4.678, 4.666, 4.656, 4.600, 4.595.
(d) 33.13 m, 33.31 m, 33.133 m, 33.331 m, 33.313 m: 33.331, 33.313, 33.31, 33.133, 33.13.
Q: Using the digits 1, 4, 0, 8, and 6 make:
(a) the decimal number closest to 30
(b) the smallest possible decimal number between 100 and 1000.
Ans: (a) Closest to 30: 30.146 (|30 − 30.146| = 0.146).
(b) Smallest between 100 and 1000: 104.68.
Q: Will a decimal number with more digits be greater than a decimal number with fewer digits?
Ans: No, the number of digits doesn’t determine size. Compare: 1.2 (fewer digits) > 0.9999 (more digits). Size depends on place value comparison.
Q: Mahi purchases 0.25 kg of beans, 0.3 kg of carrots, 0.5 kg of potatoes, 0.2 kg of capsicums, and 0.05 kg of ginger. Calculate the total weight of the items she bought.
Ans: 0.25 + 0.3 + 0.5 + 0.2 + 0.05 = 1.30 kg.
Total: 1.30 kg.
Q: Pinto supplies 3.79 L, 4.2 L, and 4.25 L of milk to a milk dairy in the first three days. In 6 days, he supplies 25 litres of milk. Find the total quantity of milk supplied to the dairy in the last three days.
Ans: First 3 days: 3.79 + 4.2 + 4.25 = 12.24 L.
Last 3 days: 25 − 12.24 = 12.76 L.
Q: Tinku weighed 35.75 kg in January and 34.50 kg in February. Has he gained or lost weight? How much is the change?
Ans: 35.75 − 34.50 = 1.25 kg.
Tinku lost 1.25 kg.
Q: Extend the pattern: 5.5, 6.4, 6.39, 7.29, 7.28, 6.18, 6.17 _______,_______.
Ans: Pattern alternates: +0.9, −0.01, +0.9, −0.01, etc.
Next: 7.07 (+0.9), 7.06 (−0.01), 7.96 (+0.9).
Q: How many millimeters make 1 kilometer?
Ans: 1 km = 1000 m = 1000 × 1000 mm = 1,000,000 mm.
Q: Indian Railways offers optional travel insurance for passengers who book e-tickets. It costs 45 paise per passenger. If 1 lakh people opt for insurance in a day, what is the total insurance fee paid?
Ans: 45 paise = ₹0.45.
1 lakh = 100,000.
Total: 100,000 × 0.45 = ₹45,000.
Q: Which is greater?
(a) 10/1000 or 1/10?
(b) One-hundredth or 90 thousandths?
(c) One-thousandth or 90 hundredths?
Ans: (a) As ¹⁰⁄₁₀₀₀ = ¹⁄₁₀₀ and ¹⁄₁₀ = ¹⁰⁄₁₀₀, so ¹⁄₁₀ > ¹⁰⁄₁₀₀₀
(b) As one-hundredth = ¹⁄₁₀₀ and
90 thousandths = ⁹⁰⁄₁₀₀₀ = ⁹⁄₁₀₀, so ⁹⁄₁₀₀ > ¹⁄₁₀₀
or 90 thousandths > One-hundredth.
(c) As one-thousandth = ¹⁄₁₀₀₀ and
90 hundredths = ⁹⁰⁄₁₀₀ = ⁹⁰⁰⁄₁₀₀₀, so ¹⁄₁₀₀₀ < ⁹⁰⁰⁄₁₀₀₀
Page no. 80
Q: Write the decimal forms of the quantities mentioned:
(a) 87 ones, 5 tenths and 60 hundredths = 88.10
(b) 12 tens and 12 tenths
(c) 10 tens, 10 ones, 10 tenths, and 10 hundredths
(d) 25 tens, 25 ones, 25 tenths, and 25 hundredths
Ans:
(a) 87 ones, 5 tenths, 60 hundredths = 87 + 0.5 + 0.60 = 88.1.
(b) 12 tens, 12 tenths = 120 + 1.2 = 121.2.
(c) 10 tens, 10 ones, 10 tenths, 10 hundredths = 100 + 10 + 1 + 0.1 = 111.1.
(d) 25 tens, 25 ones, 25 tenths, 25 hundredths = 250 + 25 + 2.5 + 0.25 = 277.75.
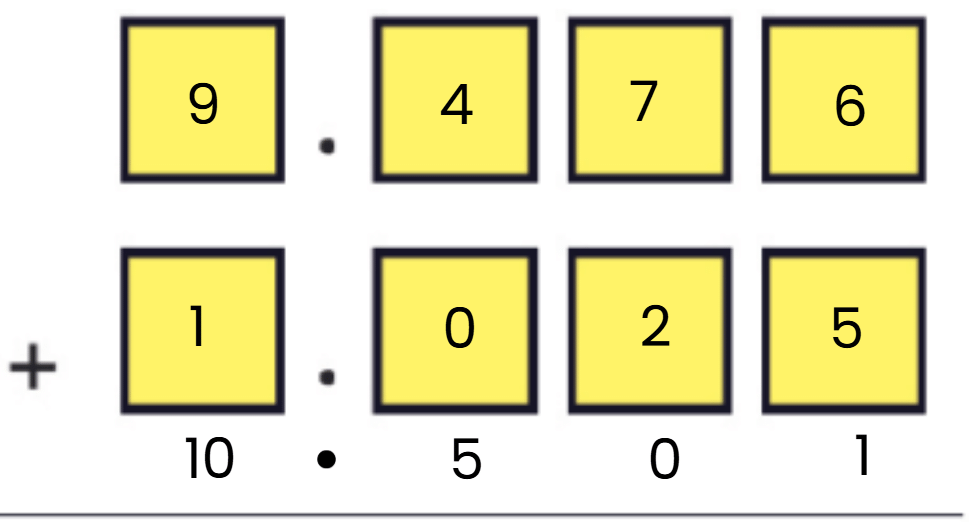
Q: Using each digit 0 – 9 not more than once, fill the boxes below so that the sum is closest to 10.5:
Ans:
Q: Write the following fractions in decimal form:
(a) 1/2
(b) 3/2
(c) 1/4
(d) 3/4
(e) 1/5
(f) 4/5
Ans: (a) ¹⁄₂ × ⁵⁄₅ = ⁵⁄₁₀ = 0.5
(b) ³⁄₂ × ⁵⁄₅ = ¹⁵⁄₁₀ = ¹⁰⁄₁₀ + ⁵⁄₁₀ = 1 + ⁵⁄₁₀ = 1.5
(c) ¹⁄₄ × ²⁵⁄₂₅ = ²⁵⁄₁₀₀ = ²⁰⁄₁₀₀ + ⁵⁄₁₀₀ = ²⁄₁₀ + ⁵⁄₁₀₀ = 0.25
(d) ³⁄₄ × ²⁵⁄₂₅ = ⁷⁵⁄₁₀₀ = ⁷⁰⁄₁₀₀ + ⁵⁄₁₀₀ = ⁷⁄₁₀ + ⁵⁄₁₀₀ = 0.75
(e) ¹⁄₅ × ²⁄₂ = ²⁄₁₀ = 0.2
(f) ⁴⁄₅ × ²⁄₂ = ⁸⁄₁₀ = 0.8