Q1: What are the five postulates of Euclid’s Geometry?
Sol: Euclid’s postulates are the basic assumptions on which Euclidean geometry is built. They are:
- A straight line may be drawn from any one point to any other point.
- A terminated straight line can be produced indefinitely in a straight line.
- A circle can be described with any centre and any radius.
- All right angles are equal to one another.
- If a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two straight lines, if produced indefinitely, meet on that side on which the sum of the angles is less than two right angles.
These five statements serve as the starting rules for classical plane geometry. The fifth postulate is often called the parallel postulate because of its relation to the existence and behaviour of parallel lines.
Q2: If in Q.2, point C is called a mid-point of line segment AB. Prove that every line segment has one and only one mid-point.
Sol:
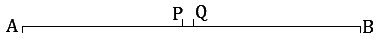
Let AB be a line segment.
Assume, for contradiction, that P and Q are two distinct mid-points of AB.
Then by definition of midpoint,
AP = PB ………(1)
and AQ = QB ……(2)
Since AP + PB = AB and AQ + QB = AB, both AP and AQ are halves of AB.
From (1), adding AP to both sides gives:
AP + AP = PB + AP (If equals are added to equals, the wholes are equal.)
⇒ 2 AP = AB …(3)
From (2), similarly:
2 AQ = AB …(4)
From (3) and (4):
2 AP = 2 AQ
⇒ AP = AQ
Hence the distances from A to P and from A to Q are equal, so P and Q coincide.
This contradicts the assumption that P and Q are different points.
Therefore every line segment has one and only one mid-point.
Hence proved.
Q3: Does Euclid’s fifth postulate imply the existence of parallel lines? Explain.
Sol:
Yes. Euclid’s fifth postulate implies the existence of parallel lines because it gives a condition under which two straight lines will never meet.
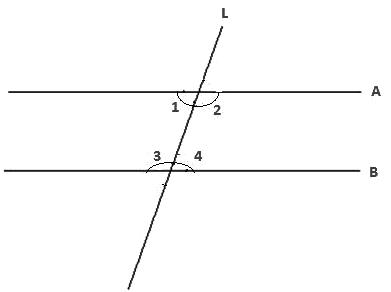
If a straight line falling on two straight lines makes the interior angles on the same side add up to two right angles (180°), then the two lines, when extended indefinitely on that side, do not meet. Such lines are defined as parallel.
Thus, when ∠1 + ∠2 = 180° (or ∠3 + ∠4 = 180° in the figure), the two lines are parallel.
Equivalently, this postulate is closely related to Playfair’s axiom, which states: through a point not on a given line there is exactly one line parallel to the given line. Both statements describe the same geometric idea in different forms.
Q4: If a point C lies between two points A and B such that AC = BC, then prove that AC =1/2 AB. Explain by drawing the figure.
Sol:
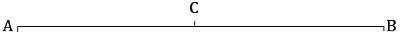
Given AC = BC and C lies between A and B, so AB = AC + CB.
Add AC to both sides of AC = BC:
AC + AC = BC + AC
2 AC = BC + AC
But BC + AC = AB (since AC and CB together make AB), therefore:
2 AC = AB
⇒ AC = 1/2 AB.
Thus AC is half of AB, so C is the midpoint of AB.
Q5: In the given figure, if AC = BD, then prove that AB = CD.
Sol:
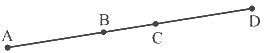
It is given that AC = BD.
From the figure, AC = AB + BC and BD = BC + CD.
Therefore,
AB + BC = BC + CD (since AC = BD)
Subtract BC from both sides (if equals are subtracted from equals, the remainders are equal):
AB = CD.
Hence proved that AB equals CD.
Q.6: It is known that x + y = 10 and that x = z. Show that z + y = 10.
Sol:
Given:
x + y = 10 …(i)
x = z …(ii)
Substitute z for x in equation (i) (if equals are substituted for equals, the results are equal):
z + y = 10.
Hence z + y = 10, as required.