Page No. 70-71
Let Us Think
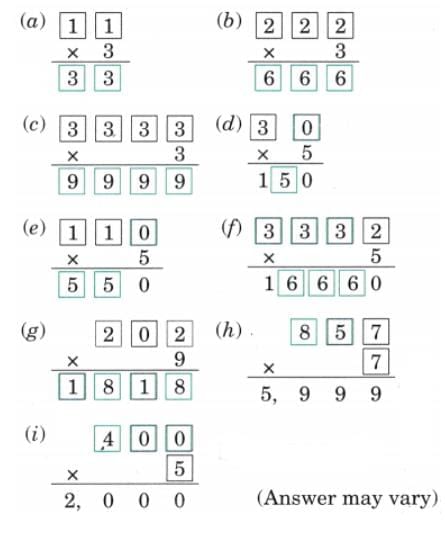
Q1: The given shapes stand for numbers between 1 and 24. The same shape denotes the same number across all problems. Find the numbers hiding in all the shapes.
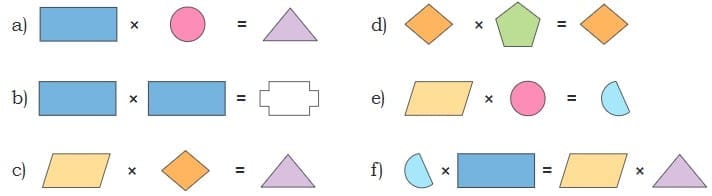
Ans: This can be solved by using a trial-and-error method while keeping the conditions consistent across all diagrams.
One valid set of values for the shapes is shown below. These values are chosen so that each equation formed by the shapes is true when substituted: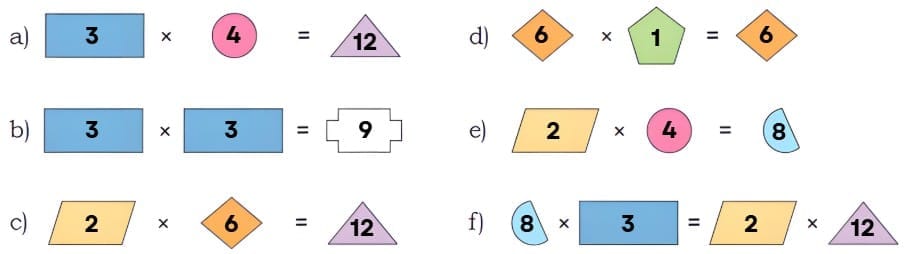
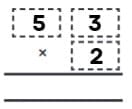
Q2: Place the digits 2, 5, and 3 appropriately to get a product close to 100. Share your reasoning in class.
Ans: If we place the digits to form 53 × 2 = 106, the product is 106. Rounding 106 to the nearest ten gives 110, which is closer to 100 than the other possible products made from the digits 2, 5 and 3.
Thus, 53 × 2 is a good choice to get a product near 100.
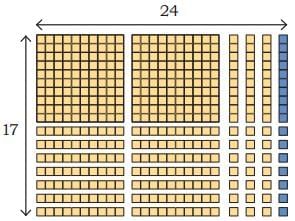
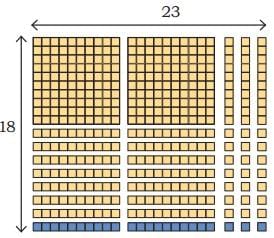
Q3: A dairy has packed butter milk pouches in the following manner. Find the number of pouches kept in each arrangement. One is done for you.

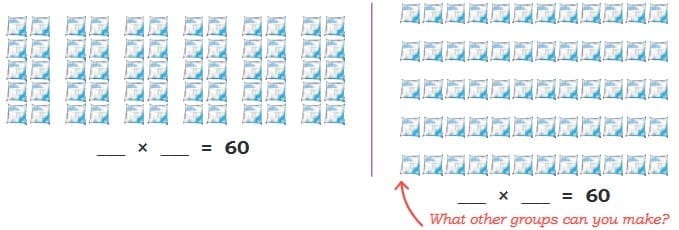
Ans:
Q4: Which number am I?
I am a two-digit number, help of the following clues.
(а) I am greater than 8.
(b) I am not a multiple of 4.
(c) I am a multiple of 9.
(d) I am an odd number.
(e) I am not a multiple of 11.
(f) I am less than 50.
(g) My ones digit is even.
(h) My tens digit is odd.
There’s a contradiction here. If it’s an odd number (clue d), its ones digit must be odd (1, 3, 5, 7, or 9). But clue (g) says its ones digit is even (0, 2, 4, 6, or 8).
A number cannot be both odd and have an even ones digit at the same time.
Ans: No, all clues were used consistently to find the number.
Clue (d) says “odd number,” while clue (g) says the ones digit is even; these two clues conflict with one another because an odd number cannot have an even ones digit. Hence, the clues are inconsistent.
Clues that would directly help narrow down the number:
- (c) Multiple of 9 – This limits options significantly
- (f) Less than 50 – Combined with being two-digit, gives range 10-49
- (d) Odd number OR (g) One’s digit is even – One of these (whichever is correct)
- (h) Tens digit is odd – Further narrows the options
Clues that might be redundant once we narrow it down:
- (a) Greater than 8 – This is already satisfied by being a two-digit number (all two-digit numbers are ≥10)
- (b) Not a multiple of 4 – This would already be satisfied if the number is odd (clue d), since odd numbers can never be multiples of 4
- (e) Not a multiple of 11 – This might eliminate one specific option, but may not be necessary
Q5: Make your own numbers.
Choose any two numbers and one operation from the grid. Try to make all the numbers between 0 and 20. For example 2 can be formed as 4 – 2. Could you make all the numbers?
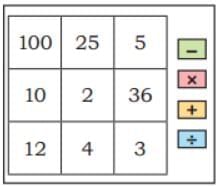
Ans: One example given is 36 – 25 = 11. (Answers will vary; try different pairs and operations to obtain numbers from 0 to 20.)
Q: Which numbers could you not make? Is it possible to make these numbers using three numbers? You can use two operations, if needed. Which numbers between 0-20 can you get in more than one way?
Ans:
Try this as a class activity: list the numbers you could not form using two numbers and one operation, then see if adding a third number or a second operation helps. Record numbers that have more than one representation.
Page No. 72-74
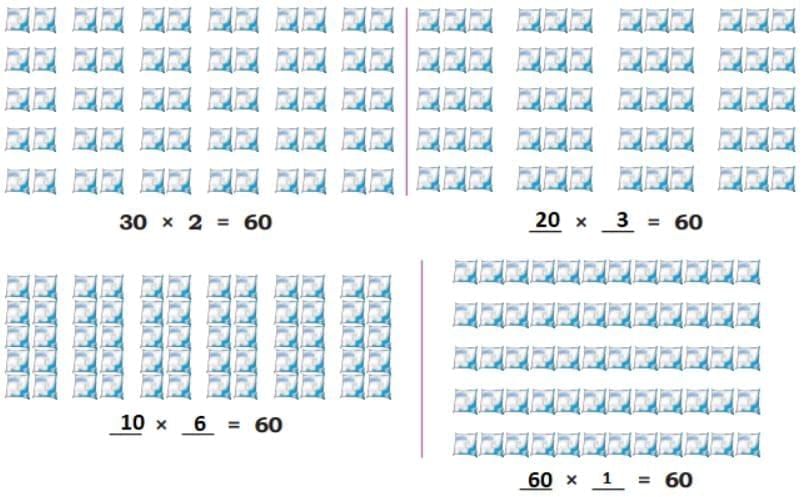
Order of Numbers in Multiplication
Q: Daljeet Kaur runs a milk processing unit. She has arranged the butter packets in the following ways. Find the number of butter packets in each case. What pattern do you notice (or observe)? Discuss in class.
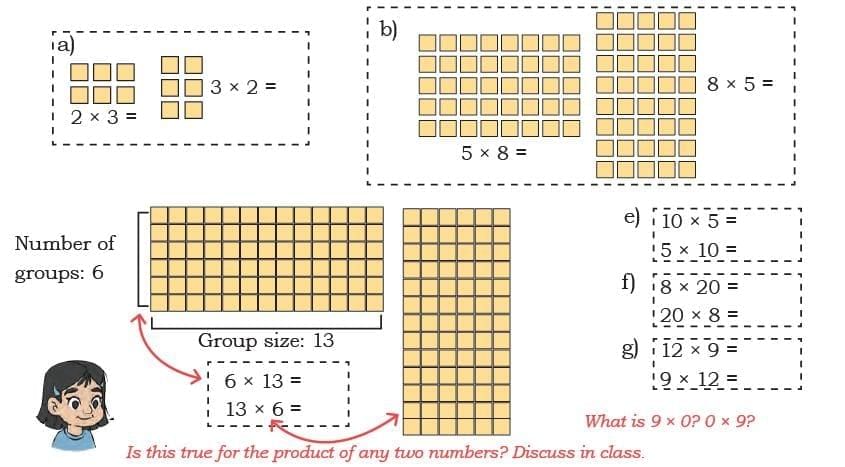
Ans:
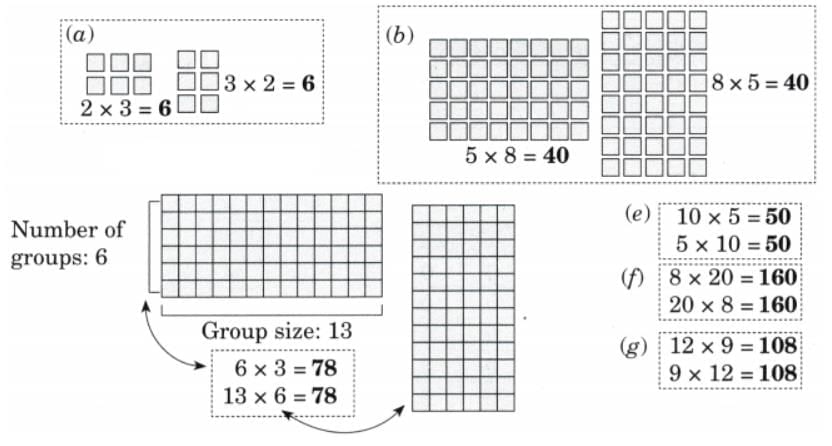
The pattern observed is that the product of two numbers remains the same when we interchange their positions; that is, multiplication is commutative: a × b = b × a.
What is 9 × 0? 0 × 9?
Ans: 9 × 0 = 0 and 0 × 9 = 0. Multiplying any number by zero gives zero.
Patterns in Multiplication by 10s and 100s
Q1: Let us revise multiplication by 10s and 100s.
(a) 4 × 10 = _____
(b) 20 × 10 = _____
(c) 10 × 40 = _____
(d) 10 × 10 = 100
(e) 20 × 50 = ______
(f) 80 × 10 = ______
(g) 3 × 100 = 100 × 3 = 300
(h) 8 × 100 = _____ = ______
(i) 10 × 100 = _____ = ______
Ans:
(a) 4 × 10 = 40
(b) 20 × 10 = 200
(c) 10 × 40 = 400
(d) 10 × 10 = 100
(e) 20 × 50 = 1000
(f) 80 × 10 = 800
(g) 3 × 100 = 100 × 3 = 300
(h) 8 × 100 = 100 × 8 = 800
(i) 10 × 100 = 100 × 10 = 1000
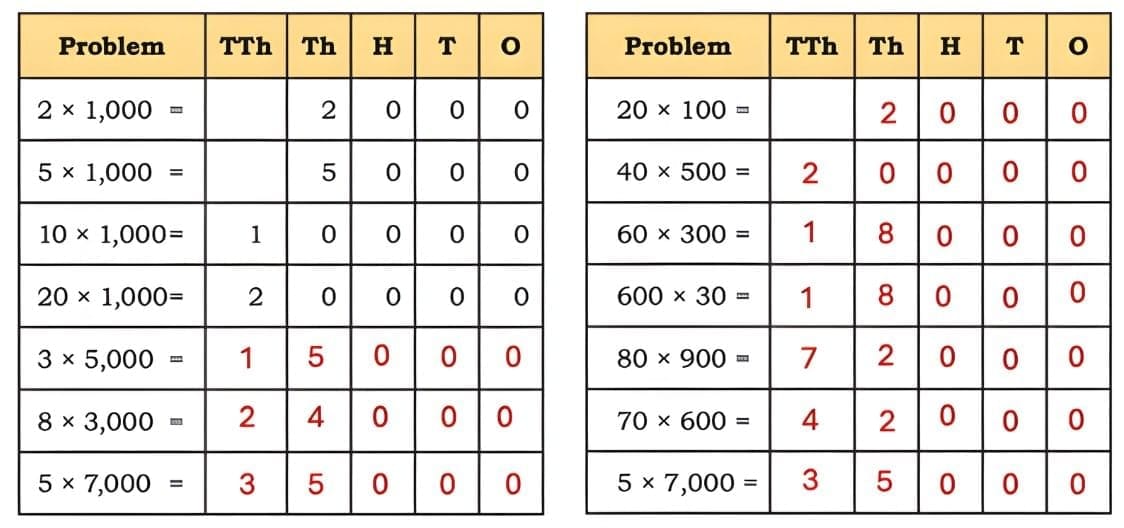
Q2: Find the answers to the following questions. Fill in the table below and describe the pattern. Discuss in class.
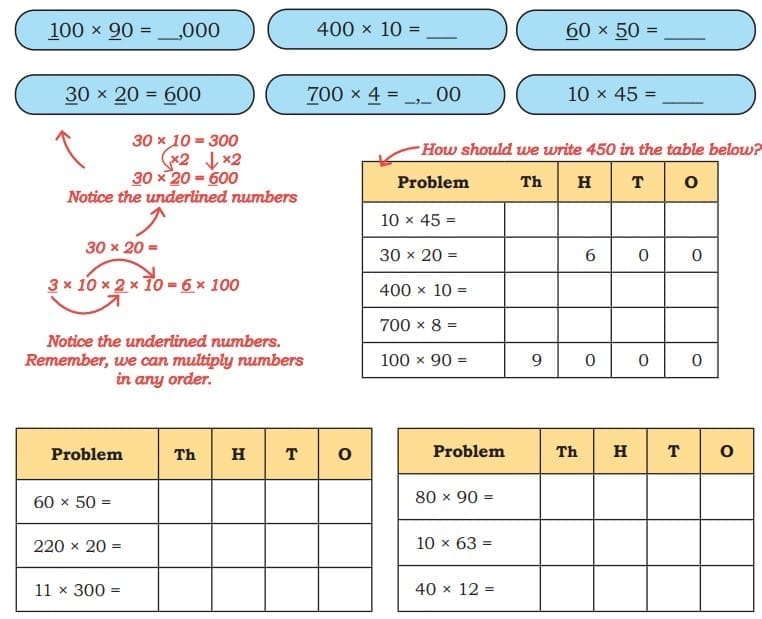
Ans:

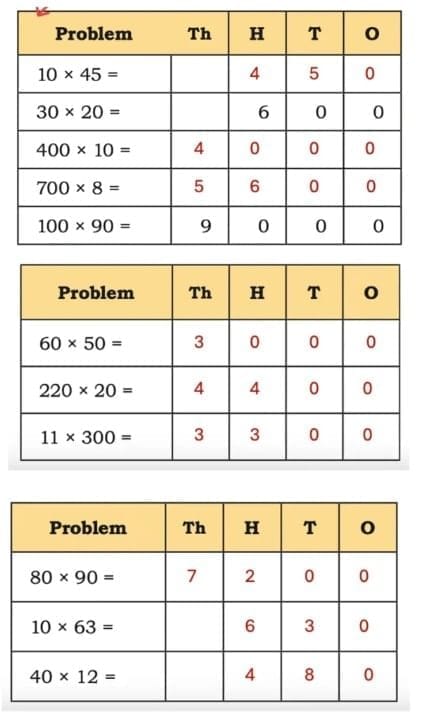
Q: Let us fill in the table and observe the patterns.
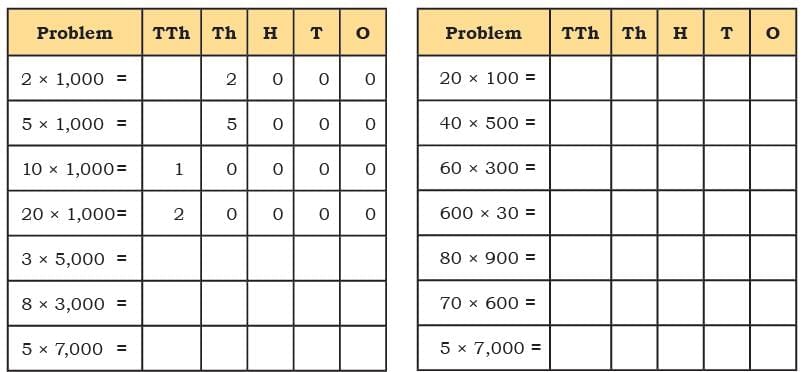
Ans:
Page No. 75-76
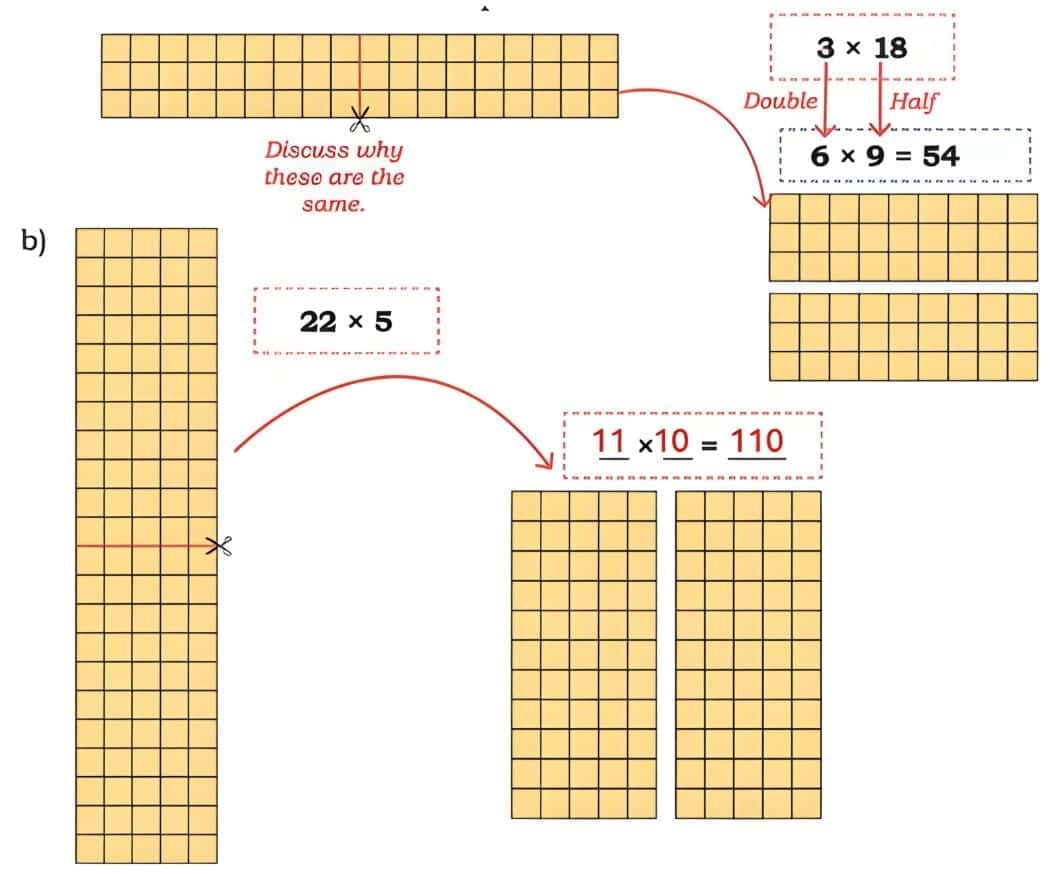
Doubling and Halving
Q: Butter packets are arranged in the following ways. Let us find some strategies to calculate the total number of packets.
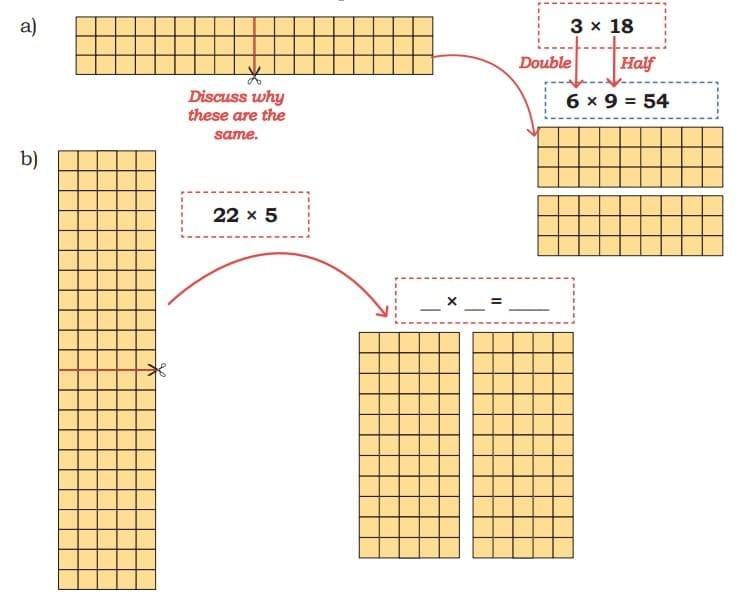
Sol:
(c) Solve the following problems like the previous ones.
Ans:
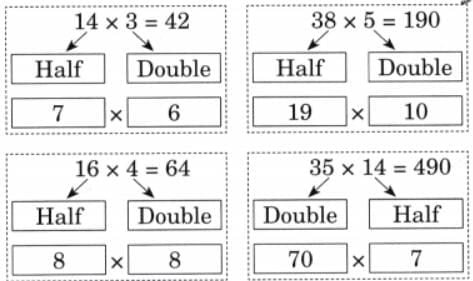
Q: This halving and doubling strategy works well when we have to multiply with numbers like 5 and 25. Discuss why?
Ans: Halving one factor and doubling the other does not change the product because (a ÷ 2) × (b × 2) = a × b. This is useful to simplify calculations when one factor becomes easier to multiply after halving or doubling.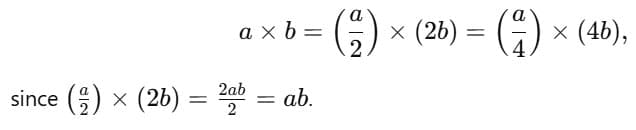
Why it works well for 5 and 25
1. For ×5:
5=102
So, for any even N,
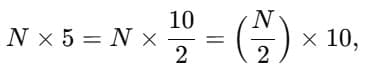
i.e. halve N and then append a zero (×10).
Example: 38×5=(19)×10=190.
2. For ×25:
25=1004
So, for any N divisible by 4,
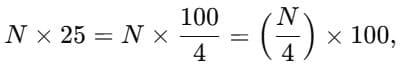
i.e. halve twice (divide by 4) and then append two zeros (×100).
Example: 84×25=(21)×100=2100
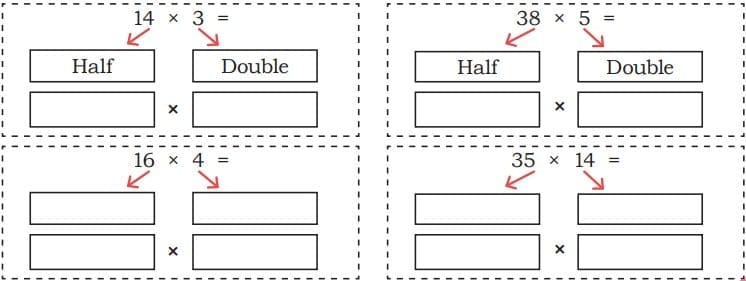
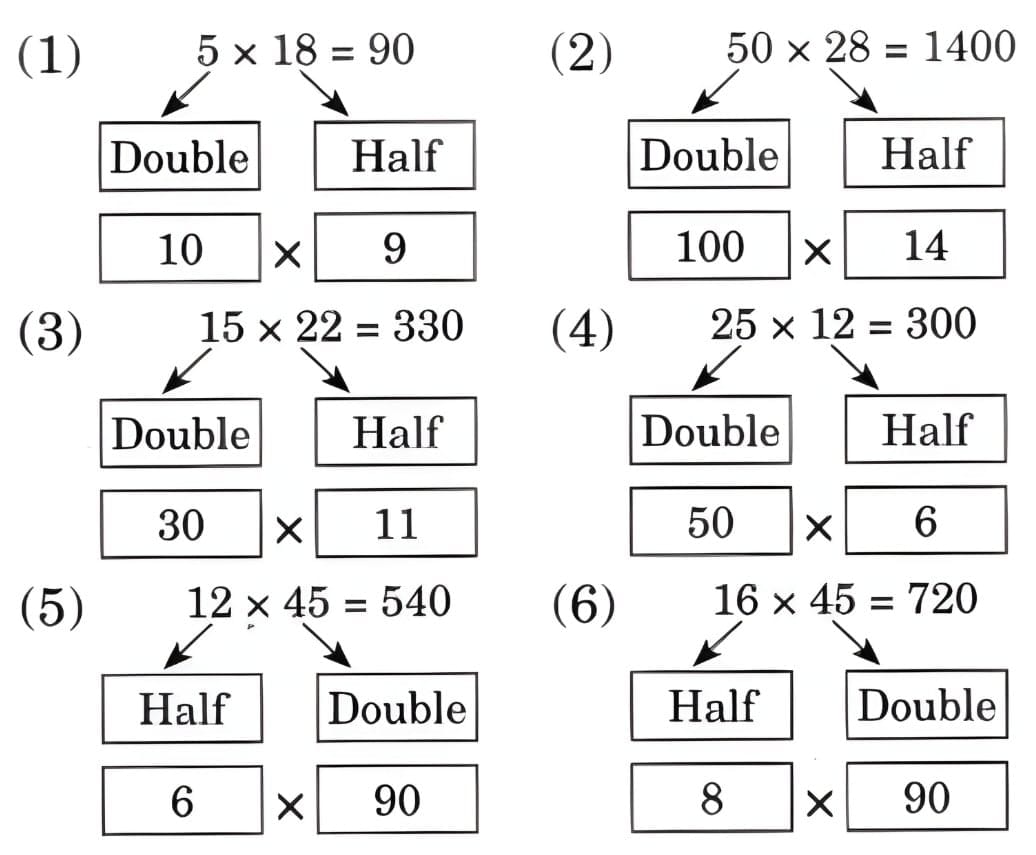
(d) Find the product by halving and doubling either the multiplier or the multiplicand.
(1) 5 × 18
(2) 50 × 28
(3) 15 × 22
(4) 25 × 12
(5) 12 × 45
(6) 16 × 45
Ans:
(e) Give 5 examples of multiplication problems where halving and doubling will help in finding the product easily. Find the products as well.
Ans:
Nearest Multiple
(a) 4 × 19

(b) 14 × 21
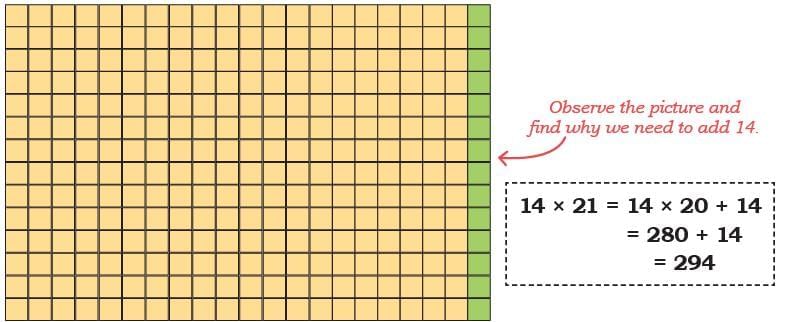
(c) Give 5 examples of problems where you can use the nearest multiple to find the product easily. Find the products as well.
Ans:
(1) 5 × 31 = 5 × 30 + 5 = 150 + 5 = 155
(2) 7 × 29 = 7 × 30 – 7 = 210 – 7 = 203
(3) 12 × 49 = 12 × 50 – 12 = 600 – 12 = 588
(4) 8 × 101 = 8 × 100 + 8 = 800 + 8 = 808
(5) 16 × 99 = 16 × 100 – 16 = 1600 – 16 = 1584
(Answer may vary)
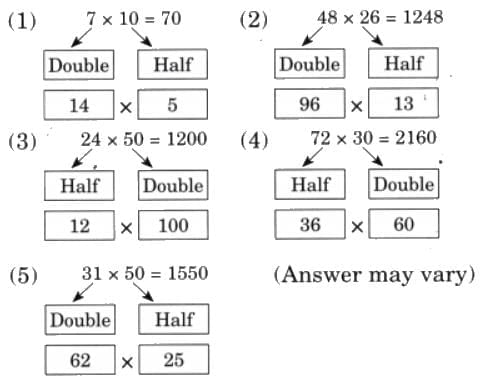
(d) Find the products of the following numbers by finding the nearest multiple.
(1) 7 × 52
(2) 12 × 28
(3) 75 × 31
(4) 99 × 15
(5) 8 × 25
(6) 22 × 42
Ans:
(1) 7 × 52 = 7 × 50 + 7 × 2 = 350 + 14 = 364
(2) 12 × 28 = 12 × 30 – 12 × 2 = 360 – 24 = 336
(3) 75 × 31 = 75 × 30 + 75 = 2250 + 75 = 2325
(4) 99 × 15 = 100 × 15 – 15 = 1500 – 15 = 1485
(5) 8 × 25 = 10 × 25 – 2 × 25 = 250 – 50 = 200
(6) 22 × 42 = 22 × 40 + 22 × 2 = 880 + 44 = 924
Page No. 77-78
Let Us Solve
Use strategies flexibly to answer the following questions. Discuss your thoughts in class.
Q1: A school has an auditorium with 35 rows, with 42 seats in each row. How many people can sit in this auditorium?
Ans:
Number of rows = 35
Number of seats in each row = 42
Total number of seats in all = 35 × 42 = 35 × 40 + 35 × 2
= 1400 + 70
= 1470
Thus, 1470 people can sit in the auditorium.
Q2: Priya jogs 4 kilometres every day. How many kilometres will she jog in 31 days?
Ans:
Priya jogs every day = 4 km
Number of kilometres she will jog in 31 days = 4 × 31 = 4 × 30 + 4 = 120 + 4 = 124 km
Thus, Priya will jog 124 km in 31 days.
Q3: A school has received 36 boxes of books with 48 books in each box. How many total books did the school receive in the boxes?
Ans:
Number of books in each box = 48
Number of boxes received by the school = 36
Total number of books received by the school = 36 × 48 = 36 × 50 – 36 × 2
= 1800 – 72
= 1728 books
Thus, the school received 1728 books in all.
Q4: Priya uses 16 metres of cloth to make 4 kurtas. How much cloth would she need to make 8 kurtas?
Ans:
Cloth needed to make 4 kurtas = 16 m
Cloth needed to make 1 kurta = 16 ÷ 4 = 4 m
Cloth needed to make 8 kurtas = 8 × 4 = 32 m.
Q5: Gollappa has 29 cows on his farm. Each cow produces 5 litres of milk per day. How many litres of milk do the cows produce in total, each day?
Ans:
Number of cows on Gollappa’s farm = 29
Milk produced by each cow = 5 litres
Total quantity of milk produced in his farm = 5 × 29 = 5 × 30 – 5 = 150 – 5 = 145 litres
Thus, 145 litres of milk are produced each day.
Q6: Maska Cow Farm has 297 cows. Each cow requires 18 kg of fodder per day. How much total fodder is needed to feed 297 cows every day?
Ans:
Total number of cows at Maska Cow Farm = 297
Fodder required by each cow = 18 kg per day
Total amount of fodder required for 297 cows = 18 × 297 = 18 × 300 – 18 × 3 = 5400 – 54
= 5346 kg
Thus, 5346 kg of fodder will be required for 297 cows every day.
Page No. 79-80
Let Us Multiply
(a) 32 × 8
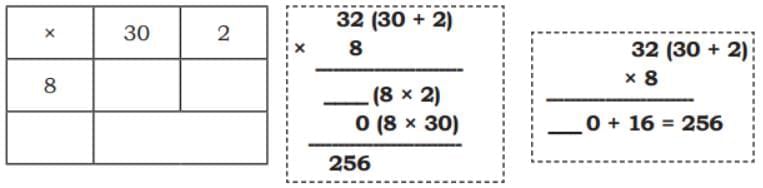
Ans:
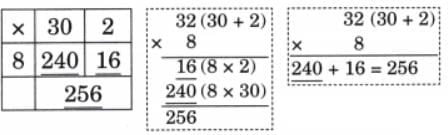
(b) 69 × 45
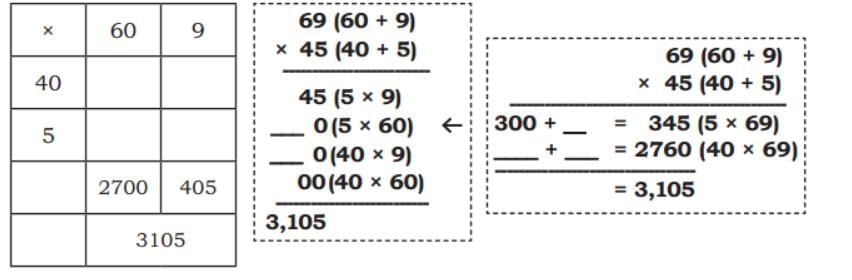
Ans:

Let Us Do
Q: Solve the following problems like Nida did.
(a)
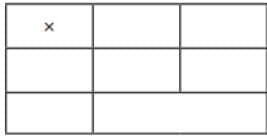
Ans:
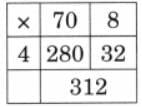
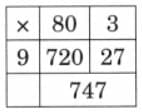
(b) 83 × 9
Ans:
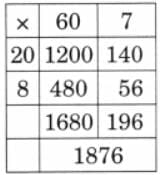
(c) 67 × 28
Ans:
(d) 53 × 37
Ans:
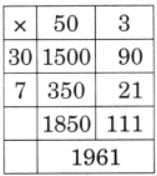
Q2: Solve the following problems like Kanti did.
(a) 94 × 5
Ans:
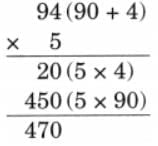
(b) 49 × 6
Ans:

(c) 37 × 53
Ans:
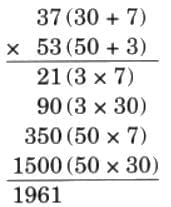
(d) 28 × 79
Ans:

Q3: Solve the following problems like John.
(a) 86 × 3
Ans:
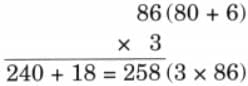
(b) 72 × 7
Ans:
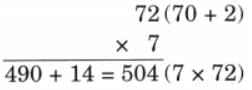
(c) 94 × 36
Ans:

(d) 66 × 22
Ans:
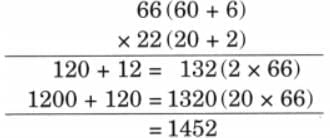
Q4: Solve the following problems:
(a) A movie theatre has 8 rows of seats, and each row has 12 seats. If half the seats are filled, how many people are watching the movie? If 3 more rows get filled, how many total people will be there?

Ans:
Number of rows of seats in the movie theatre = 8
Number of seats in each row = 12
Since, half seats are filled, that is 4 rows out of 8 are filled.
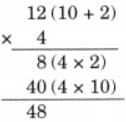
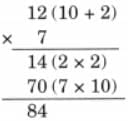
So, number of people who watched the movie = 4 × 12
Thus, 48 people watched the movie.
Now, 3 more rows get filled.
Therefore, number of people who will watch the movie = 7 × 12
Thus, 84 people will be there, if 3 more rows get filled.
(b) In a test match between India and West Indies, the Indian team hit twenty- four 4s and eighteen 6s across the two innings. How many runs were scored in 4s and 6s each? 234 runs were made by running between the wickets. If 23 runs were extras, how many runs were scored by Indian team in the two innings?
Ans:
In the test match, number of 4s hit by Indian team = 24
Therefore, runs scored by Indian team by hitting 4s = 24 × 4 = 96 runs
In the test match, number of 6s hit by Indian team = 18
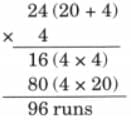
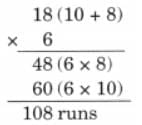
Therefore, runs scored by Indian team by hitting 6s = 18 × 6 = 108 runs
Runs scored by running between the wickets = 234 runs
Runs scored by extras = 23 runs
Therefore, total runs scored by the Indian team in two innings = 96 + 108 + 234 + 23 = 461 runs
(c) Anjali buys 15 bulbs and 12 tube lights from Sudha Electricals. Each bulb costs ₹25 and each tube light costs ₹34. How much money should Anjali give to the shopkeeper?
Ans:
Cost of 15 bulbs = 15 × ₹ 25 = ₹ 375
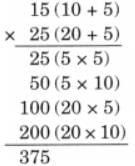
Cost of 12 tube lights = 12 × ₹ 34 = ₹ 408
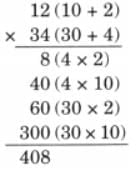
Total cost of 15 bulbs and 12 tube lights = ₹ 375 + ₹ 408 = ₹ 783
Thus, Anjali will give ₹ 783 to the shopkeeper to buy 15 bulbs and 12 tube lights.
(d) A shopkeeper sold 28 bags of rice. Each bag costs ?350. How much money did he earn by selling rice bags?
Ans:
The cost of each rice bag = ₹ 350
Since, a shopkeeper sold 28 bags of rice.

Therefore, total cost of 28 bags of rice = 350 × 28 = ₹ 9800
Thus, the shopkeeper earned ₹ 9800 by selling 28 bags of rice.
(e) A school library has 86 shelves and each shelf has 162 books. Find the number of books in the library.
Ans:
Number of shelves in the library = 86 (80 + 6)
Number of books in each shelf = 162 (100 + 60 + 2)
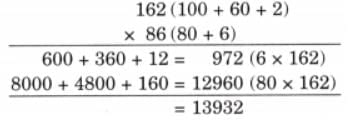
Therefore, the total number of books in the library = 162 × 86 = 13932
Page No. 83-84
Let Us Do
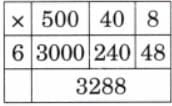
Q1: Solve the following problems like Nida did.
a) 548 × 6
Ans:
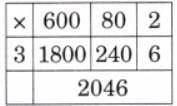
b) 682 × 3
Ans:
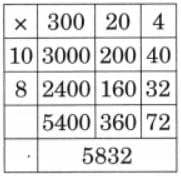
(c) 324 × 18
Ans:
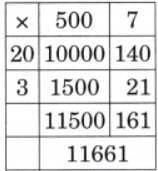
(d) 507 × 23
Ans:
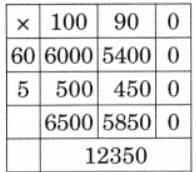
(e) 190 × 65
Ans:
Q2: Solve the following problems like John.
(a) 123 × 84
Ans:

(b) 368 × 32
Ans:
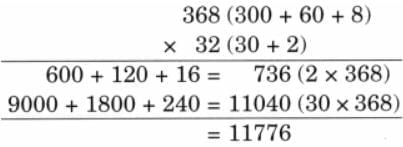
(c) 159 × 324
Ans:

(d) 239 × 401
Ans:
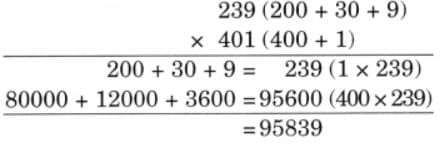
(e) 592 × 5
Ans:
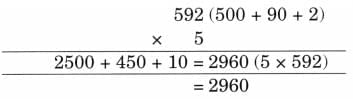
(f) 101 × 22
Ans:
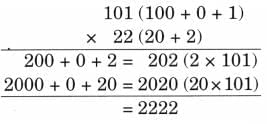
Q3: Let us solve a few questions like Milli’s father.
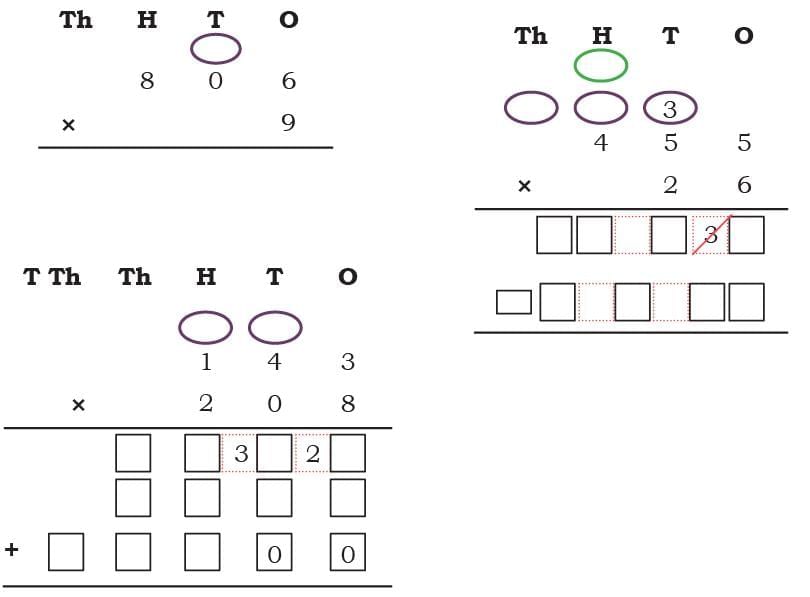
Ans:
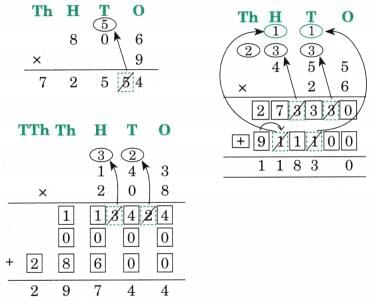
Now use Mili’s father’s method to solve the following questions.
(a) 807 × 5
Ans:
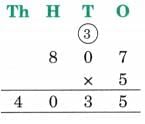
(b) 143 × 28
Ans:
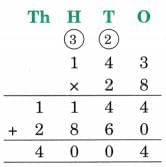
(c) 309 × 9
Ans:
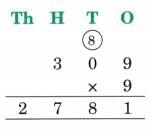
(d) 450 × 38
Ans:
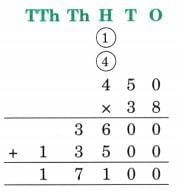
(e) 584 × 23
Ans:

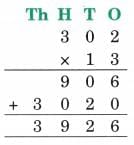
(f) 302 × 13
Ans:
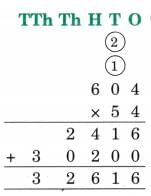
(g) 604 × 54
Ans:
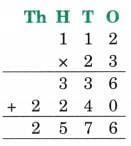
(h) 112 × 23
Ans:
(i) 237 × 19
Ans:
Page No. 85
Check, Check!
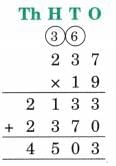
Check if the following children’s solutions are correct. If correct, explain why the solution is correct. If it is incorrect, then identify the error and correct the solution.
(a) Asma’s solutions for 46 × 59

Ans:
Asma broke the multiplication into parts correctly and added the partial products. Her final result is correct. Only the order of the partial products shown is reversed, but addition is commutative so the final sum remains the same.

(b) Pankaj’s solution for 203 × 54
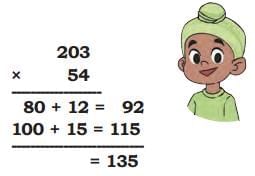
Ans:
Pankaj made a place-value error: he used 20 instead of 200 and 5 instead of 50 when forming partial products. This gives an incorrect final product. The correct method is to use the actual place values (200 and 50) when making the partial products.

(c) Lado’s solution for 38 × 150
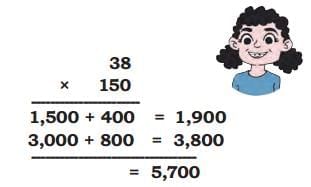
Ans:
She split 38 as 30 + 8 and 150 as 100 + 50 and then multiplied each part correctly. Her decomposition and final sum of partial products are correct.
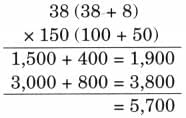
(d) Kira’s solution for 193 × 272
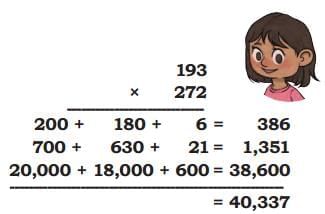
Ans:
Kira broke the first number correctly, but she used 7 instead of 70 in one partial product for the second number. That is a place-value mistake. The correct partial products must use 70 (tens) and 200 (hundreds).
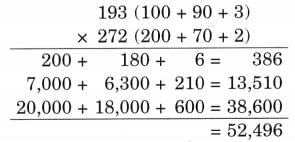
(e) Asher’s solution
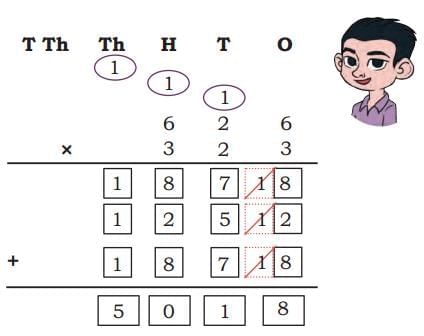
Ans:
Asher made an error identifying place values in 323: the digits 3 and 2 stand for hundreds, tens and ones as 300, 20 and 3. Correctly using these place values, 626 × 323 = 202,198.
Page No. 86-90
Let Us Do
Q1: Identify the problems that have the same answer as the one given at the top of each box. Do not calculate.

Ans:

Q2: Find easy ways of solving these problems.
(a) 16 × 25
Ans:

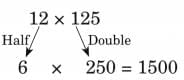
(b) 12 × 125
Ans:
(c) 24 × 250
Ans:

(d) 36 × 25
Ans:
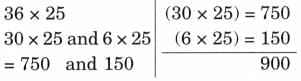
(e) 28 × 75
Ans:
28 × 75 = 30 × 75 – 150
= 2250 – 150
= 2100
(f) 300 × 15
Ans:
300 × 15 = 4500
(g) 50 × 78
Ans:
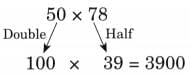
(h) 199 × 63
Ans:
199 × 63 = 200 × 63 – 63
= 12600 – 63
= 12537
(i) 128 × 35
Ans:
128 × 35 = 130 × 35 – 70
= 4550 – 70
= 4480
Q3: Write 5 other examples for which you can find easy ways of getting products.
Ans:
(a) 201 × 19
= 200 × 19 + 19
= 3800 + 19
= 3819
(b) 149 × 25
= 150 × 25 – 25
= 3750 – 25
= 3725
(c) 25 × 78
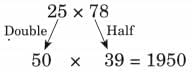
(d) 28 × 18
= 30 × 18 – 18 × 2
= 540 – 36
= 504
(e) 998 × 4
= 1000 × 4 – 8
= 4000 – 8
= 3992
(Answer may vary)
Q4: Find the answers to the following questions based on the given information.
(a) 17 × 23 = 391
(b) 17 × 24 = _______
(c) 17 × 22 = _______
(d) 16 × 23 = _______
(e) 8 × 9 = 72
(f) 18 × 9 = _______
(g) 28 × 9 = _______
(h) 108 × 9 = _______
(i) 18 × 23 = _______
Ans:
(a) 17 × 23 = 391
(b) 17 × 24 = 408
(c) 17 × 22 = 374
(d) 16 × 23 = 368
(e) 8 × 9 = 72
(f) 18 × 9 = 162
(g) 28 × 9 = 252
(h) 108 × 9 = 972
To find 17 × 24, how much is to be added to 17 × 23 _____ 17 or 23?
Ans:
17 × 24 = 17 × 23 + (17) = 391 + (17)
To find 18 × 23, how much is to be added to 17 × 23 _____ 17 or 23?
Ans:
18 × 23 = 17 × 23 + (23)
= 391 + (23)
= 414
Let Us Think
Q1: Find the possible values of the coloured boxes in each of the following problems. The same colour indicates the same number in a problem. Some problems can have more than one answer.
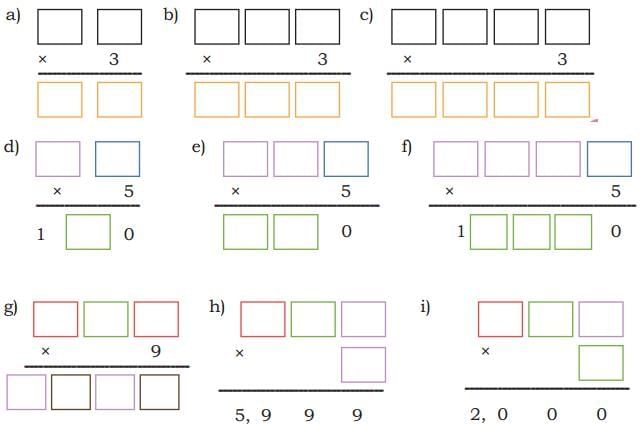
Ans:
Q2: Estimate the products on the left and match them to the numbers given on the right.
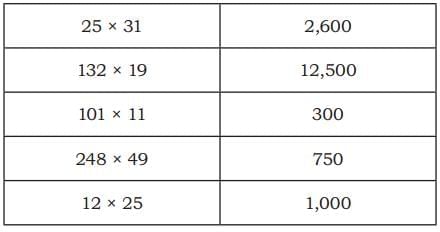
Ans:
The King’s Reward
One day, a king decided to reward three of his most talented ministers. The king called them to his court and said, “You all have served my empire with great dedication. As a reward, I give you three choices of gold.
Which of the rewards would you have chosen?
Ans:
Do it yourself.
After a week, the 3 ministers were surprised at the final amount of gold coins. Guess who received the most gold coins? Calculate how much gold
Ans:
Minister-1
5 × 1 = 5 → Day 1
5 × 2 = 10 → Day 2
10 × 2 = 20 → Day 3
20 × 2 = 40 → Day 4
40 × 2 = 80 → Day 5
80 × 2 = 160 → Day 6
160 × 2 = 320 → Day 7
Minister-2
3 × 1 = 3 → Day 1
3 × 3 = 9 → Day 2
9 × 3 = 27 → Day 3
27 × 3 = 81 → Day 4
81 × 3 = 243 → Day 5
243 × 3 = 729 → Day 6
729 × 3 = 2187 → Day 7
Minister-3
1 × 1 = 1 → Day 1
1 × 5 = 5 → Day 2
5 × 5 = 25 → Day 3
25 × 5 = 125 → Day 4
125 × 5 = 625 → Day 5
625 × 5 = 3125 → Day 6
3125 × 5 = 15625 → Day 7
Minister 1 received 320 gold coins, minister 2 received 2187 coins and minister 3 received 15625 coins.
Hence, minister 3 received most number of gold coins.
Multiplication Patterns
Q1: Notice how the multiplier, multiplicand, and products are changing in each of the following. What is the relationship of the new product with the original product?- Solve (a) completely, and then predict the answers for the rest.
(a) 16 × 44 = 704
(1) 8 × 88 = 704
(2) 8 × 22 = 176
(3) 16 × 22 = ______
(4) 32 × 44 = ______
Ans:
(a) 16 × 44 = 704
(1) 8 × 88 = 704
(2) 8 × 22 = 176
(3) 16 × 22 = 352
(4) 32 × 44 = 1408
b) 12 × 32 = 384
(1) 6 × 16 = ______
(2) 24 × 16 = ______
(3) 24 × 64 = ______
(4) 12 × 16 = ______
Ans:
12 × 32 = 384
(1) 6 × 16 = 96
(2) 24 × 16 = 384
(3) 24 × 64 = 1536
(4) 12 × 16 = 192
Q2: Observe and complete the given patterns.
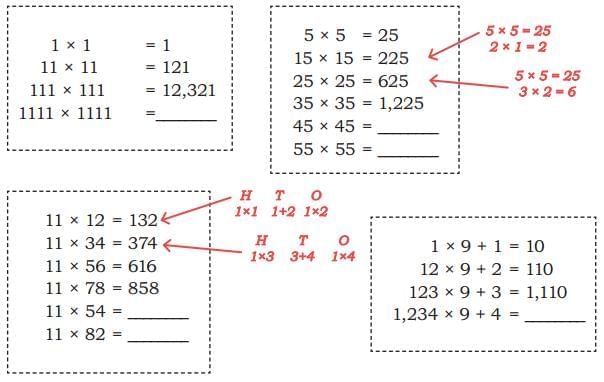
Ans:
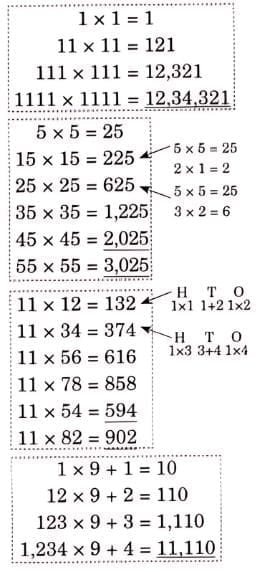
Here are some numbers.
Remember number pairs from Grade 4? Any two adjacent numbers in a row or a column are number pairs. Can you identify the pair whose product is the smallest and another pair whose product is the largest? Do you need to find every product or can you find this by looking at the numbers?
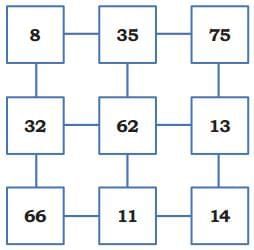
Ans:
Use reasoning to identify the smallest and largest products: the smallest product will come from the smallest adjacent numbers and the largest product from the largest adjacent numbers. (Do this activity by inspection and a few multiplications as needed.)
Page No. 91
Let Us Solve
Q1: Mala went to a book exhibition and bought 18 books. The shop was selling 3 books for ₹ 150. After buying the books, she still had ₹ 20 left. How much money did Mala have at the beginning?
Ans:
The number of books bought by Mala = 18
Since, the cost of 3 books is ₹ 150.
So, the cost of 1 book = ₹ 150 ÷ 3 = ₹ 50
Therefore, the total cost of 18 books = 18 × 50 = (20 × 50) – (2 × 50) = 1000 – 100 = 900
So, the cost of 18 books = ₹ 900
Since, Mala still had ₹ 20 left, the amount she had at the beginning = ₹ 900 + ₹ 20 = ₹ 920.
Q2: A village sports club organises a women’s football tournament. The club earned money by selling match tickets and charging fees for team participation.
They sold 57 tickets for ₹ 115 each.
They had 3 teams joining the tournament, with each team paying a participation fee of ₹ 1,599.
The teams paid ₹ 1,750 in total rent the football ground and ₹ 1,129 for food and water.
(a) How much money did the club collect in total from ticket sales and team participation fees?
(b) What were the total expenses on renting the ground and food and water?
Ans:
Money collected by selling tickets = ₹ (57 × 115) = ₹ (60 × 115 – 3 × 115) = ₹ (6900 – 345) = ₹ 6555
Deposit of participation fees by the 3 teams = ₹ (3 × 1599) = ₹ (3 × 1600 – 3) = ₹ 4800 – 3 = ₹ 4797
Rent paid for the football ground by the teams in total = ₹ 1750
Cost of food and water for the teams = ₹ 1129
(a) The total money collected by the club from the ticket sales and team participation fees = ₹ 6555 + ₹ 4797 = ₹ 11,352
(b) Total expenses on renting the ground and food and water = ₹ 1750 + ₹ 1129 = ₹ 2879
Q3: Ananya is watching Republic Day celebrations on city’s public ground. There are 12 rows of students sitting in front of her and 17 rows behind her. There are 18 students to her right and 22 students to her left.
(a) How many rows of students are there in total?
(b) How many students are there in Ananya’s row?
(c) What is the total number of students on the ground?
Ans:
(a) Number of rows of students in the ground = 12 + 1 + 17 = 30 rows (include Ananya’s row).
(b) Number of students in Ananya’s row = 18 + 1 + 22 = 41 students (include Ananya).
(c) Total number of students on the ground = 30 × 41 = 1230
Q4: Multiply.
(a) 67 × 78
(b) 34 × 56
(c) 45 × 263
(d) 86 × 542
(e) 432 × 107
(f) 310 × 120
Ans:
(a) 67 × 78 = 67 × 80 – 2 × 67
= 5360 – 134
= 5226
(b) 34 × 56 = 30 × 56 + 4 × 56
= 1680 + 224
= 1904
(c) 45 × 263 = 40 × 263 + 5 × 263
= 10,520 + 1315
= 11,835
(d) 86 × 542 = 86 × (540 + 2)
= 86 × 540 + 2 × 86
= 46,440 + 172
= 46,612
(e) 432 × 107 = 432 × 100 + 432 × 7
= 43,200 + 3024
= 46,224
(f) 310 × 120 = 300 × 120 + 10 × 120
= 36,000 + 1200
= 37,200
Q5: If 67 × 67 = 4489, without multiplication find 67 × 68.
Ans:
Since, 67 × 67 = 4489
∴ 67 × 68 = 67 × 67 + 67 = 4489 + 67 = 4556
Q6: If 99 × 100 = 9900, without multiplication find 99 × 99.
Ans:
Since, 99 × 100 = 9900
∴ 99 × 99 = 99 × 100 – 99 = 9900 – 99 = 9801