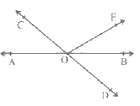
Q1: In the figure, lines AB and CD intersect at O. If ∠AOC + ∠BOE = 70° and ∠BOD = 40°, find ∠BOE and reflex ∠COE.
Ans:
At point O three adjacent angles on a straight line add to 180°.
So, ∠AOC + ∠BOE + ∠COE = 180°.
Given ∠AOC + ∠BOE = 70°, substitute to get:
70° + ∠COE = 180°
∴ ∠COE = 110°.
Now consider the other straight line through O: ∠COE + ∠BOD + ∠BOE = 180°.
Substitute ∠COE = 110° and ∠BOD = 40°:
110° + 40° + ∠BOE = 180°
∴ ∠BOE = 180° – 150° = 30°.
The reflex angle ∠COE is the larger angle at O corresponding to ∠COE, so reflex ∠COE = 360° – 110° = 250°.
Hence, ∠BOE = 30° and reflex ∠COE = 250°.
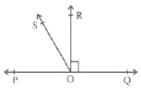
Q2: In the Figure, POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that ∠ROS = 1/2(∠QOS – ∠POS).
Ans:
POQ is a straight line, so the three adjacent angles on that line sum to 180°:
∠POS + ∠ROS + ∠ROQ = 180°.
Given OR ⟂ PQ, so OR is perpendicular to the straight line POQ. Hence ∠POR = ∠ROQ = 90°. In particular ∠ROQ = 90°.
Substitute ∠ROQ = 90° into the previous equation:
∠POS + ∠ROS + 90° = 180°
∴ ∠POS + ∠ROS = 90°. (1)
Now ∠QOS is formed by ∠QOR + ∠ROS. But ∠QOR = ∠ROQ = 90°, so
∠QOS = 90° + ∠ROS.
Rearrange this to get:
∠QOS – ∠ROS = 90°. (2)
From (1) and (2) we have:
∠POS + ∠ROS = ∠QOS – ∠ROS
Bring like terms together:
2∠ROS + ∠POS = ∠QOS
Therefore ∠ROS = 1/2(∠QOS – ∠POS), as required.
Q3: In the Figure, if AB || CD, EF ⊥ CD and ∠GED = 126°, find ∠AGE, ∠GEF and ∠FGE.
Ans:
Since AB ∥ CD and GE is a transversal, alternate interior angles are equal. Therefore
∠AGE = ∠GED = 126°.
At point E on line EF, ∠GED is split as ∠GEF + ∠FED. Given EF ⟂ CD, we have ∠FED = 90°.
So, ∠GEF = ∠GED – ∠FED = 126° – 90° = 36°.
Also, ∠FGE and ∠GED are a linear pair (they lie on a straight line through G), so
∠FGE + ∠GED = 180°.
Hence ∠FGE = 180° – 126° = 54°.
Therefore,
∠AGE = 126°, ∠GEF = 36° and ∠FGE = 54°.
Q4: In Fig. 6.33, PQ and RS are two mirrors placed parallel to each other. An incident ray AB strikes the mirror PQ at B, the reflected ray moves along the path BC and strikes the mirror RS at C and again reflects back along CD. Prove that AB || CD.
Ans:
Draw normals BE and CF at the points of incidence B and C respectively, so BE ⟂ PQ and CF ⟂ RS. Since PQ ∥ RS, their normals BE and CF are also parallel: BE ∥ CF.
By the law of reflection, angle of incidence = angle of reflection at each mirror. So at B:
∠(AB, BE) = ∠(EB, BC). Label these ∠1 = ∠2. At C:
∠(BC, CF) = ∠(CF, CD). Label these ∠3 = ∠4.
Because BE ∥ CF and BC is a transversal cutting them at B and C, alternate interior angles are equal. Thus ∠2 = ∠3.
Combine equalities: ∠1 = ∠2 and ∠2 = ∠3 and ∠3 = ∠4, so ∠1 = ∠4.
Angles ∠1 and ∠4 are the angles that AB and CD make with the common direction of the mirrors. Since these corresponding angles are equal, AB ∥ CD (alternate interior/corresponding angle test).
Thus AB is parallel to CD.
Q5: In the figure, if AB || CD || EF, PQ || RS, ∠RQD = 25° and ∠CQP = 60°, then find ∠QRS.
Ans:
Given PQ ∥ RS and the transversal through Q and C, angles ∠PQC and ∠BRS are alternate interior angles, so they are equal. Thus ∠BRS = ∠PQC = 60°. (i)
Given AB ∥ CD and the transversal QR, angles ∠DQR and ∠QRA are alternate interior angles, so ∠QRA = ∠DQR = 25°. (ii)
Angles ∠ARS and ∠BRS form a linear pair on line RS, so ∠ARS + ∠BRS = 180°. Using (i):
∴ ∠ARS = 180° – 60° = 120°. (iii)
Now ∠QRS = ∠QRA + ∠ARS. Using (ii) and (iii):
∠QRS = 25° + 120° = 145°.
Hence ∠QRS = 145°.
Q6: In the Figure, lines XY and MN intersect at O. If ∠POY = 90° and a : b = 2 : 3, find c.
Ans:
Angles on a straight line add to 180°, so along the line through P-O-Y we have:
∠POY + a + b = 180°. Given ∠POY = 90°, so a + b = 90°.
Given a : b = 2 : 3, let a = 2x and b = 3x. Then 2x + 3x = 90° ⇒ 5x = 90° ⇒ x = 18°.
Thus a = 2×18° = 36° and b = 3×18° = 54°.
From the diagram b and c form a straight angle on the other line, so b + c = 180°. Substitute b = 54°:
c + 54° = 180° ⇒ c = 126°.
Therefore c = 126°.
Q7: It is given that ∠XYZ = 64° and XY is produced to point P. Draw a figure from the given information. If ray YQ bisects ∠ZYP, find ∠XYQ and reflex ∠QYP.
Ans:
Since XY is produced to P, XP is a straight line. Therefore ∠XYZ + ∠ZYP = 180°.
Given ∠XYZ = 64°, so ∠ZYP = 180° – 64° = 116°.
Ray YQ bisects ∠ZYP, so each part is half of 116°: ∠ZYQ = ∠QYP = 58°.
Now ∠XYQ = ∠XYZ + ∠ZYQ = 64° + 58° = 122°.
The reflex angle ∠QYP is the larger angle at Y from Q to P around Y: reflex ∠QYP = 360° – (minor ∠QYP). The minor ∠QYP = 58°, so
reflex ∠QYP = 360° – 58° = 302°. (Equivalently, reflex ∠QYP = 180° + ∠XYQ = 180° + 122° = 302°.)
Hence ∠XYQ = 122° and reflex ∠QYP = 302°.
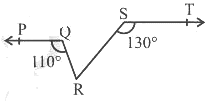
Q8: In the Figure, if PQ || ST, ∠PQR = 110° and ∠RST = 130°, find ∠QRS.
[Hint: Draw a line parallel to ST through point R.]
Ans:
Through R draw a line XY parallel to PQ (and hence parallel to ST).
Angles on the same side of a transversal add to 180°. For transversal QR with PQ ∥ XY:
∠PQR + ∠QRX = 180° ⇒ ∠QRX = 180° – 110° = 70°.
For transversal RS with ST ∥ XY:
∠RST + ∠SRY = 180° ⇒ ∠SRY = 180° – 130° = 50°.
On the straight line XY at R the three adjacent angles satisfy:
∠QRX + ∠QRS + ∠SRY = 180°.
Substitute the known angles: 70° + ∠QRS + 50° = 180° ⇒ ∠QRS = 180° – 120° = 60°.
Thus ∠QRS = 60°.
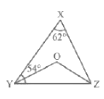
Q9: In Fig. 6.40, ∠X = 62°, ∠XYZ = 54°. If YO and ZO are the bisectors of ∠XYZ and ∠XZY respectively of Δ XYZ, find ∠OZY and ∠YOZ.
Ans:
Sum of interior angles of ΔXYZ: ∠X + ∠XYZ + ∠XZY = 180°.
Substitute ∠X = 62° and ∠XYZ = 54° to get:
62° + 54° + ∠XZY = 180° ⇒ ∠XZY = 180° – 116° = 64°.
ZO bisects ∠XZY, so ∠OZY = 1/2 × 64° = 32°.
YO bisects ∠XYZ, so ∠OYZ = 1/2 × 54° = 27°.
Now the angles in triangle OYZ sum to 180°:
∠OZY + ∠OYZ + ∠YOZ = 180° ⇒ 32° + 27° + ∠YOZ = 180°.
Therefore ∠YOZ = 180° – 59° = 121°.
Hence ∠OZY = 32° and ∠YOZ = 121°.