Very Short Answer Questions
Ques 1: The phenomenon of motion was placed on a sound scientific footing by two scientists. Write their names.
Ans: Galileo Galilei and Isaac Newton. Galileo laid the experimental foundations of kinematics and Newton formulated the laws of motion that provided a systematic explanation of how and why bodies move.
Ques 2: Are rest and motion absolute or relative terms?
Ans: They are relative terms. Whether an object is at rest or in motion depends on the chosen reference point or frame of reference.
Ques 3: Suppose a ball is thrown vertically upwards from a position P above the ground. It rises to the highest point Q and returns to the same point P. What is the net displacement and distance travelled by the ball?
Ans: Displacement is zero because the initial and final positions are the same. Distance travelled is twice the separation between P and Q, since the ball goes from P to Q and then back from Q to P.
Ques 4: Which speed is greater: 30 m/s or 30 km/h?
Ans: 30 m/s. (30 km/h = 30 × 1000/3600 m/s = 8.33 m/s, which is much less than 30 m/s.)
Ques 5: What do you mean by 2 m/s2?
Ans: It means the velocity of the body increases by 2 m/s every second. If the acceleration is negative, the speed would decrease by 2 m/s every second.
Ques 6: Can uniform linear motion be accelerated?
Ans: No. Uniform linear motion means constant velocity, so the acceleration is zero. Any non-zero acceleration changes the velocity and therefore the motion is not uniform.
Ques 7: Define one radian.
Ans: One radian is the angle subtended at the centre of a circle by an arc whose length is equal to the radius of the circle. (One radian ≈ 57.3°.)
Ques 8: What is the relation between linear velocity and angular velocity
Ans: Linear velocity = Angular velocity × Radius of the circular path. (v = ω × r)
Short Answer Questions
Ques 1: Give an example of a body that may appear to be moving for one person and stationary for the other.
Ans: Passengers in a moving bus see trees, buildings and people on the roadside appearing to move backward, while a person standing on the roadside sees the bus and its passengers moving forward. At the same time, each passenger may see fellow passengers sitting beside them as stationary. This illustrates that motion is relative and depends on the observer’s reference frame.
Ques 2: How can we describe the location of an object?
Ans: To describe the position of an object we specify a reference point called the origin and, when needed, a reference direction. For example, saying a library is 2 km north of the railway station locates the library with respect to the railway station, which acts as the reference point.
Ques 3: What do you mean by average speed? What are its units?
Ans: Average speed is the total distance travelled divided by the total time taken. If a body covers total distance D in time t, average speed = D/t. The SI unit is metre per second (m s-1).
Ques 4: What is the difference between uniform velocity and non-uniform velocity?
Ans: Uniform velocity: An object has uniform velocity when it covers equal distances in equal intervals of time in a specified direction; its speed and direction are constant. Example: a car moving at 40 km h-1 towards west with no change in speed or direction.
Non-uniform velocity: An object has non-uniform velocity if it covers unequal distances in equal time intervals or if its direction changes. Example: the blades of a revolving fan move at constant speed but their velocity is non-uniform because the direction keeps changing.
Ques 5: Differentiate between distance and displacement.
Ans: 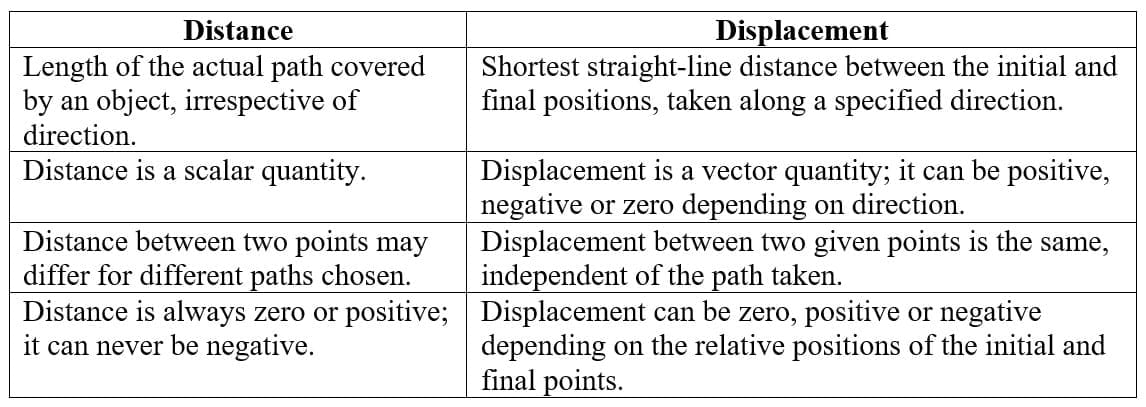
Ques 6: What are the uses of a distance-time graph?
Ans: The uses of a distance-time graph are:
(a) It shows the position of the body at any instant of time.
(b) From the graph we can read the distance covered by the body during a chosen time interval.
(c) The slope of the distance-time graph gives the speed of the body at any instant, so the graph gives information about how the speed changes with time.
Long Answer Questions
Ques 1: With the help of a graph, derive the relation v = u + at.
Ans:
Consider the velocity-time graph of an object that moves under uniform acceleration as shown in the figure (u≠0).
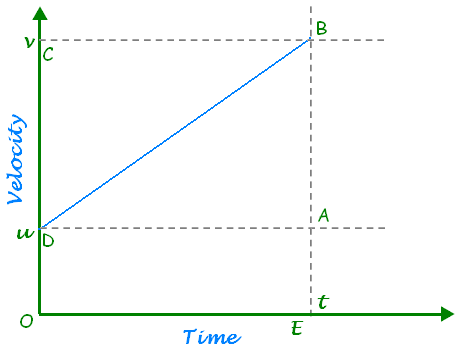
From this graph, we can see that initial velocity of the object (at point D) is u and then it increases to v (at point B) in time t. The velocity changes at uniform rate a. As shown in the figure, the lines BC and BE are drawn from point B on the time and the velocity axes respectively.
The initial velocity is represented by OD.
The final velocity is represented by BE.
The time interval t is represented by OE.
BA = BE – EA, represents the change in velocity in time interval t.
If we draw DA parallel to OE, we observe that BE = BA + DE = BA + OD
Substituting, BE with v and OD with u, we get
v = BA + u
or, BA = v – u — (i)
Thus, from the given velocity-time graph, the acceleration of the object is given by Change in velocity
a = (Change in velocity)/(Time Taken)= BA/DA= BA/OE
Substituting OC with t, we get
a = BA/t ⇒ BA = at — (ii2)
From equations (1) and (2), we have
v-u = at or v =u + at
Ques 2: Obtain a relation for the distance travelled by an object moving with a uniform acceleration in the interval between 4th and 5th seconds.
Ans: Use the equation of motion for distance from rest with initial velocity u and constant acceleration a:
s(t) = u × t + 1/2 × a × t2.
Distance travelled in first 5 s, s(5) = u × 5 + 1/2 × a × 52 = 5u + 25/2 a.
Distance travelled in first 4 s, s(4) = u × 4 + 1/2 × a × 42 = 4u + 8a.
Distance covered during the interval between 4th and 5th seconds = s(5) – s(4)
= (5u + 25/2 a) – (4u + 8a)
= u + (25/2 – 16/2) a
= u + 9/2 a.
Thus the distance travelled in the fifth second is u + 9/2 a (metres, if u in m s-1 and a in m s-2).