Multiple Choice Questions
Q1: If AD = BC and ∠ BAD = ∠ ABC, then ∠ ACB is equal to
(a) ∠ABD
(b) ∠ BAD
(c) ∠BAC
(d) ∠BDA
Ans: (d)
In △ABC and △ABD
AD =BC (given)
∠ BAD = ∠ ABC (Given)
AB = AB (Common side)
∴ △ABC ≅ △ABD (by SAS congruency)
By CPCT theorem, ∠ACB=∠BDA.
Q2: If O is a midpoint of AB and ∠BQO = ∠APO, then ∠OAP is equal to
(a) ∠QPA
(b) ∠OQB
(c) ∠QBO
(d) ∠BOQ
Ans: (c)
In △AOP and △BOQ,
AO = BO (O is the midpoint of AB)
∠APO = ∠BQO (given)
∠AOP = ∠BOQ (vertically opposite angles)
∴ △AOP ≅ △BOQ (by AAS congruency)
By CPCT, ∠OAP = ∠QBO.
Q3: If △ABC is an isosceles triangle, AB = AC,∠ B = 65º, then find ∠ A.
(a) 60º
(b) 70º
(c) 50º
(d) none of these
Ans: (c)
Since △ABC is an isosceles triangle,
∴ ∠B = ∠C
∴ ∠B = 65°
∴ ∠C = 65°
Using the angle sum property of a triangle,
∠A + ∠B + ∠C = 180°
∴ ∠A + 65° + 65° = 180°
∴ ∠A + 130° = 180°
∴ ∠A = 180° − 130° = 50°
Q4: An angle is 14º more than its complement. Find its measure.
(a) 42
(b) 32
(c) 52
(d) 62
Ans: (c)
Two angles whose sum is 90° are called complementary angles.
Let the first angle be x.
Its complement = 90° − x.
According to the question,
x = 14° + (90° − x)
x = 104° − x
⇒ 2x = 104°
⇒ x = 52°
∴ The angle is 52°.
Q5: If ABCD is a quadrilateral where AD = CB, AB = CD, and ∠ D = ∠ B, then ∠CAB is equal to
(a) ∠ACD
(b) ∠CAD
(c) ∠ACD
(d) ∠BAD
Ans: (c)
In △ABC and △CDA,
CB = AD (given)
AB = CD (given)
∠B = ∠D (given)
∴ △ABC ≅ △CDA (by SAS congruency)
By CPCT theorem,
∠CAB = ∠ACD.
Q6: If AB ⊥BC and ∠A =∠C, then the correct statement will
(a) AB ≠ AC
(b) AB = BC
(c) AB = AD
(d) AB = AC
Ans: (b)
In △ABC, ∠A = ∠C.
Opposite sides to equal angles are also equal.
Therefore, AB = BC.
Q7: If AB = AC and ∠BAC = 120°, find ∠B.
(a) 50°
(b) 60°
(c) 70°
(d) none of these
Ans: (b)
Given AB = AC,
Therefore, ∠ABC = ∠ACB = x.
In △ABC,
∠A + ∠B + ∠C = 180° (sum of angles of a triangle)
120° + x + x = 180°
2x = 60°
x = 30°
Then, ∠B = ∠C = 30°.
Answer the following questions
Q1: AD and BC are equal perpendiculars to a line segment AB. Show that CD bisects AB.
Ans: In ΔAOD and ΔBOC,
BC = AD (given)
∠OAD = ∠OBC = 90°
Since BC || AD
∠ODA = ∠OCB (alternate angles are equal)
So, ΔAOD ≅ ΔBOC (by the ASA congruence rule)
OD = OC (CPCT)
AO = OB (CPCT)
Therefore, CD bisects AB.
Q2: AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB. Show that
(i) ΔDAP ≌ ΔEBP
(ii) AD = BE
Ans. (i) ΔIn DAP and ΔEBP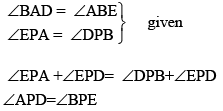
P is its mid-point of AB
∴ AP = PB
So, ΔDAP ≌ ΔEBP(by the ASA congruence rule)
(ii) AD = BE(CPCT)
Q3: In an isosceles triangle ABC with AB = AC, D and E are points on BC such that BE = CD. Show that AD = AE.
Ans: In ΔABD and ΔACE,
AB = AC (Given) ..(1)
∠B = ∠C (Angles opposite to equal sides) ..(2)
Also, BE = CD..(3)
So, BE – DE = CD – DE
That is, BD = CE (3)
So, ΔABD ≌ ΔACE by SAS rule
(Using (1), (2), (3) and SAS rule).
This gives AD = AE (CPCT)
Q4: In Figure OA = OB and OD = OC.
Show that
(i) ΔAOD ≅ ΔBOC
(ii) AD || BC
Ans: (i) In ΔAOD and ΔBOC,
OA = OB (given)
OD = OC (given)
∠AOD = ∠BOC (pair of vertically opposite angles)
So, ΔAOD ≅ ΔBOC(by the SAS congruence rule)
(ii) ∠OAD = ∠OBC (CPCT)
and these form a pair of alternate angles for line segments AD and BC.
Therefore, AD || BC.
Q5: In Fig, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.
Ans. In ΔABC and ΔADE,
AB = AD (given)
AC = AE (given)
∠BAD = ∠EAC (given)
∠ADC+ ∠BAD = ∠ADC + ∠EAC
∠BAC = ∠DAE
So, ΔABC ≌ ΔADE (by the SAS congruence rule)
BC = DE (CPCT)
Q6: In ΔABC, the bisector AD of ∠A is perpendicular to side BC. Show that AB = AC and ΔABC is isosceles.
Ans: In ΔABD and ΔADC
AD bisects ∠A
⇒ ∠BAD = ∠CAD
∠ADC = ∠ADB 90º
AD = AD (Common Side)
So, ΔABD ≌ ΔADC (by the SAS congruence rule)
AB = AC(CPCT)
∴ ΔABC is isosceles
Q7: ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal. Show that
(i) ΔABE ≌ ΔACF
(ii) AB = AC, i.e., ABC is an isosceles triangle.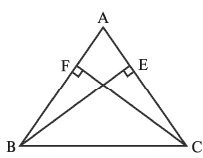
BE = CF (given)
∠A = ∠A (common angle)
∠ABE = ∠ACF (both are right angles)
So, ΔABE ≅ ΔACF (by ASA congruence rule).
This gives AB = AC (CPCT).
∴ ABC is an isosceles triangle.