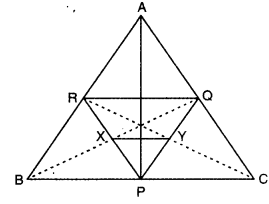
Q1: In the figure, P, Q and R are the mid-points of the sides BC, AC and AB of ΔABC. If BQ and PR intersect at X and CR and PQ intersect at Y, then show that XY = 1/4 BC.
Ans:
R and Q are mid-points of AB and AC respectively.
∴ By the mid-point theorem, RQ || BC and RQ = 1/2 BC.
Also P is the mid-point of BC, so BP = PC = 1/2 BC.
Thus RQ ∥ BP and RQ = BP.
Consider quadrilateral BPQR with vertices B-P-Q-R.
Since one pair of opposite sides (BP and RQ) are equal and parallel, BPQR is a parallelogram.
Therefore its diagonals PR and BQ bisect each other, so X (the intersection of PR and BQ) is the mid-point of PR.
Similarly, in quadrilateral PCQR, the opposite sides PC and RQ are equal and parallel, so PCQR is a parallelogram.
Hence its diagonals PQ and CR bisect each other, so Y (the intersection of PQ and CR) is the mid-point of PQ.
Now, in ΔPQR, X and Y are mid-points of PR and PQ respectively.
Therefore XY is parallel to RQ and XY = 1/2 · RQ (mid-point theorem applied in ΔPQR).
But RQ = 1/2 BC, so XY = 1/2 · (1/2 BC) = 1/4 BC.
Thus XY = 1/4 BC.
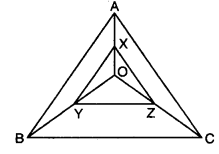
Q2: In ΔABC, AB = 8 cm, BC = 9 cm and AC = 10 cm. X, Y and Z are mid-points of AO, BO and CO respectively as shown in the figure. Find the lengths of the sides of ΔXYZ.
Ans:
Given AB = 8 cm, BC = 9 cm and AC = 10 cm.
In ΔAOB, X and Y are mid-points of AO and BO respectively.
∴ By the mid-point theorem, XY = 1/2 · AB = 1/2 × 8 cm = 4 cm.
In ΔBOC, Y and Z are mid-points of BO and CO respectively.
∴ YZ = 1/2 · BC = 1/2 × 9 cm = 4.5 cm.
In ΔCOA, Z and X are mid-points of CO and AO respectively.
∴ ZX = 1/2 · AC = 1/2 × 10 cm = 5 cm.
Hence the sides of ΔXYZ are XY = 4 cm, YZ = 4.5 cm and ZX = 5 cm.
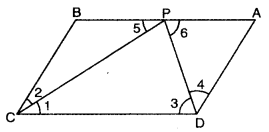
Q3: ABCD is a parallelogram. If the bisectors DP and CP of angles D and C meet at P on side AB, then show that P is the mid-point of side AB.
Ans:
Ans:
Let DP and CP bisect ∠D and ∠C respectively.
So the two halves of ∠D are equal and the two halves of ∠C are equal.
Since AB ∥ DC and CP is a transversal, an angle formed at P with AB is equal to the corresponding half of ∠C. Hence an angle at B in triangle BCP equals the corresponding half of ∠D. Therefore, in triangle BCP two angles are equal, which implies BC = BP. (angles opposite equal sides are equal and conversely)
Similarly, since AB ∥ DC and DP is a transversal, an angle at A in triangle ADP equals the corresponding half of ∠D and so in triangle ADP two angles are equal; hence DA = AP.
But in a parallelogram opposite sides are equal, so BC = AD.
From BC = BP, DA = AP and BC = AD, we get BP = AP.
Hence P is the mid-point of AB.
Q4: In the figure, ΔBCD is a trapezium in which AB || DC. E and F are the mid-points of AD and BC respectively. DF and AB are produced to meet at G. Also, AC and EF intersect at the point O. Show that :
(i) EO || AB
(ii) AO = CO
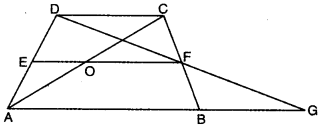
Ans:
F is the mid-point of BC, so BF = FC.
Lines DF and AB are produced to meet at G, so points D, F, G are collinear.
Consider triangles BFG and CFD:
BF = FC, ∠BFG = ∠CFD (vertical angles), and ∠BGF = ∠CDF (alternate interior angles, as AB ∥ DC).
Thus ΔBFG ≅ ΔCFD by AAS, and so DF = FG.
Since D, F, G are collinear and DF = FG, F is the mid-point of DG.
Now, in ΔAGD, E is the mid-point of AD and F is the mid-point of DG.
By the mid-point theorem, EF ∥ AG.
But G lies on AB, so AG is a segment of AB; therefore EF ∥ AB and, in particular, EO (part of EF) ∥ AB. This proves (i).
Because AB ∥ DC, EF ∥ AB implies EF ∥ DC as well. In ΔADC, E is the mid-point of AD and EO ∥ DC, so the line through the mid-point E parallel to DC bisects AC. Hence O is the mid-point of AC and AO = CO. This proves (ii).
Q5: PQRS is a square and ∠ABC = 90° as shown in the figure. If AP = BQ = CR, then prove that ∠BAC = 45°
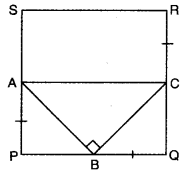
Ans:
In square PQRS, all sides are equal, so PQ = QR. (1)
Given AP = BQ = CR. Subtracting the equal lengths BQ and CR from PQ and QR respectively gives:
PQ – BQ = QR – CR ⇒ PB = QC. (2)
In ΔAPB and ΔBQC:
AP = BQ (given), ∠APB = ∠BQC = 90° (angles in a square), and PB = QC (from (2)).
So ΔAPB ≅ ΔBQC by SAS congruence.
Hence AB = BC. In ΔABC, if AB = BC, the base angles opposite those equal sides are equal; let each be x°.
Then ∠B + ∠ACB + ∠BAC = 180° ⇒ 90° + x + x = 180° ⇒ 2x = 90° ⇒ x = 45°.
Therefore ∠BAC = 45°.
Q6: In the given figure, AE = DE and BC || AD. Prove that the points A, B, C and D are concyclic. Also, prove that the diagonals of the quadrilateral ABCD are equal.
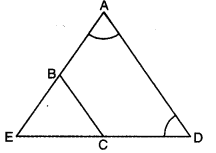
Ans:
Since AE = DE
∠D = ∠A …. (i) [∵ ∠s opp. to equal sides of a Δ]
Again, BC || AD
∠EBC = ∠A …. (ii) (corresponding ∠s]
From (i) and (ii), we have
∠D = ∠EBC …. (iii)
But ∠EBC + ∠ABC = 180° (a linear pair]
∠D + ∠ABC = 180° (using (iii)]
Now, a pair of opposite angles of quadrilateral ABCD is supplementary
Thus, ABCD is a cyclic quadrilateral i.e., A, B, C and D’are concyclic. In ΔABD and ΔDCA
∠ABD = ∠ACD [∠s in the same segment for cyclic quad. ABCD]
∠BAD = ∠CDA [using (i)]
AD = AD (common]
So, by using AAS congruence axiom, we have
ΔABD ≅ ΔDCA
Hence, BD = CA [c.p.c.t.]