Worksheet Solutions: Circles

True and False

Q1: If two arc of a circle are congruent. Then corresponding chord are unequal.
Ans: False (Corresponding chords are equal)

Q2:  Two perpendicular bisector of chord intersect at center of circle.
Ans: True ( each perpendicular bisector of chord passes through the center so center is common point for the two perpendicular bisectors of the chords)

Q3: The line joining the mid-point of a chord to centre perpendicular to chord. 
Ans: True (A line joining the mid-point of a chord to the centre of circle, perpendicular to the chord)

Q4: It is possible to draw two circles from three non-collinear points.
Ans: False (One and only one circle can be passed through three co-linear points in a plane.)

Answer the following Questions

Q1: If O is the center of circle of radius 5 cm OP perpendicular to AB and OQ perpendicular to CD, AB||CD, AB = 6cm and CD = 8 cm. Determine PQ.
Ans: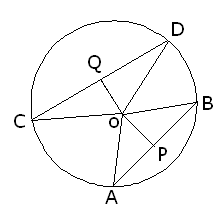

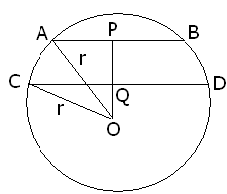
Q2: AB and CD are the two chords of the circle such that AB = 6 cm, CD = 12 cm and AB||CD, if the distance between AB and CD is 3 cm, find the radius of the circle.
Ans:

Q3: Prove that the line joining to the centre of circle to the mid-point of a chord, is perpendicular to the chord.
Ans:

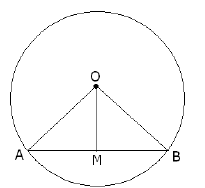
O is the centre of the circle and AB is the Chord ,OM is the line segment intersecting at M , Mid point of AB

In ΔAMO and ΔBMO

AM = BM (M is the mid point of AB)

OA = OB (radius of circle)

OM = OM (Same side)

Hence

ΔAMO ≌ ΔBMO (By SSS)

∠AMO = ∠BMO ( BY C.P.C.T)

∠AMO +∠ BMO = 180 (linear pair angles)

∠AMO = 90

Q4: Given an arc of circle how you will find its centre and complete the circle.
Ans:

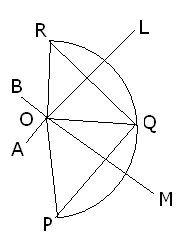Construction : 

Step 1: Take 3 points P,Q,R on circumference of arc join P to Q and R to Q

Step 2: Draw Perpendicular bisector of line PQ and RQ these intersect at point O

Step 3: join O to P , O to Q and O to R

O is the centre of given arc where OQ and OR and OP are the radius of circle

Q5: Two equal chord AB and CD of circle with center O, when produced meet at a point E, proving that BE=DE and AE=CE
Ans:

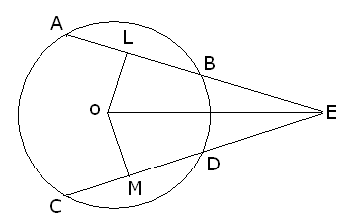
Let OL and OM be two perpendiculars from centre O to chord AB and CD respectively so L and M are the mid points of Chord AB and CD

Since AB = CD (Given)

AB/2 = CD/2 or LB = MD

In ΔOLE and ΔOME

OL = OM (Equal Chords having equal distance from the centre)

<OLE = <OME (both 90 degrees)

OE = OE (common side)

So BY R.H.S

ΔOLE ≌ ΔOME

So LE = ME ( by C.P.C.T)

LE = LB+BE

ME = MD+DE

LB+BE = MD+DE

But LB = MD (proved above)

So BE = DE

Q6: Two equal circles intersect in P and Q. A straight line through P meets the circles in A and B. prove that QA=QB
Ans:

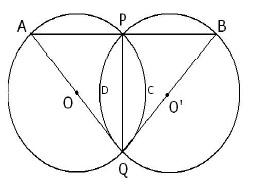
Let O and O’ be the centre of the circle where C(o, r) ≌ C(o’, r) circles are equal

So PQ is the common arc in both the circle

arc(PDQ) = arc(PCQ)

<QAP = <QBP (equal chords make equal angles on the circles)

in triangle ABQ <A = <B

so

Side AQ = Side BQ (Sides opposite to equal sides are equal)