Introduction
Have you ever gone on a long trip and wondered how far you travelled or how long it took? Think about where you went, how you got there, and how different your journey would have been a hundred or even a thousand years ago.

Bullock Carts
Human beings have always been curious explorers. Since ancient times, they have travelled great distances—initially on foot, then using animals like horses, camels, or bullocks. One of the earliest inventions in transport was the boat, even before bullock carts became common. Boats helped early humans cross rivers, lakes, and seas, opening up new lands and trade routes.

Bicycle
About a hundred years ago, the number of vehicles was very small. People mostly used animal-drawn carts, simple cars, and trains. But over the years, the modes of transport have changed drastically. Today, we have millions of vehicles—cars, buses, motorcycles, airplanes, ships—and this number continues to rise every day.
Reading and Writing Large Numbers


Imagine you have a lot of things, like thousands of candies! How do we write such big numbers?
Let’s start with 1,000.
What numbers do we get when we keep adding a thousand?
If we keep adding 1,000, we get these numbersWhat happens when we add 1,000 to 9,000?
We get Ten Thousand, which is written as 10,000.
To understand big numbers, we use something called a Place Value Chart. It helps us know the value of each digit in a number.
Look at the table below and notice the pattern of writing numbers.
Place Value ChartWe add a new column called TTh, which stands for Ten Thousand.
Here’s how it works:

This is 1

• 10 Ones make 1 Ten (10)
• 10 Tens make 1 Hundred (100)
• 10 Hundreds make 1 Thousand (1,000)
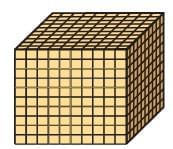
• 10 Thousands make 1 Ten Thousand (10,000)
We use commas to make large numbers easier to read.
For example, 10,000 is read as “Ten Thousand.”
We use the digits from 0 to 9 in different places to write even larger numbers.
For example:
• 1,380 = 1 Thousand + 3 Hundreds + 8 Tens + 0 Ones.

1,380
• 9,123 = 9 Thousands + 1 Hundred + 2 Tens + 3 Ones.
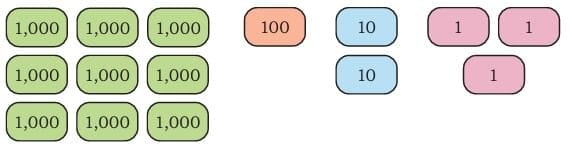
9,123
Let us see how we write numbers beyond 10,000 and how we name them. We write them in the same way as numbers below 9,999.
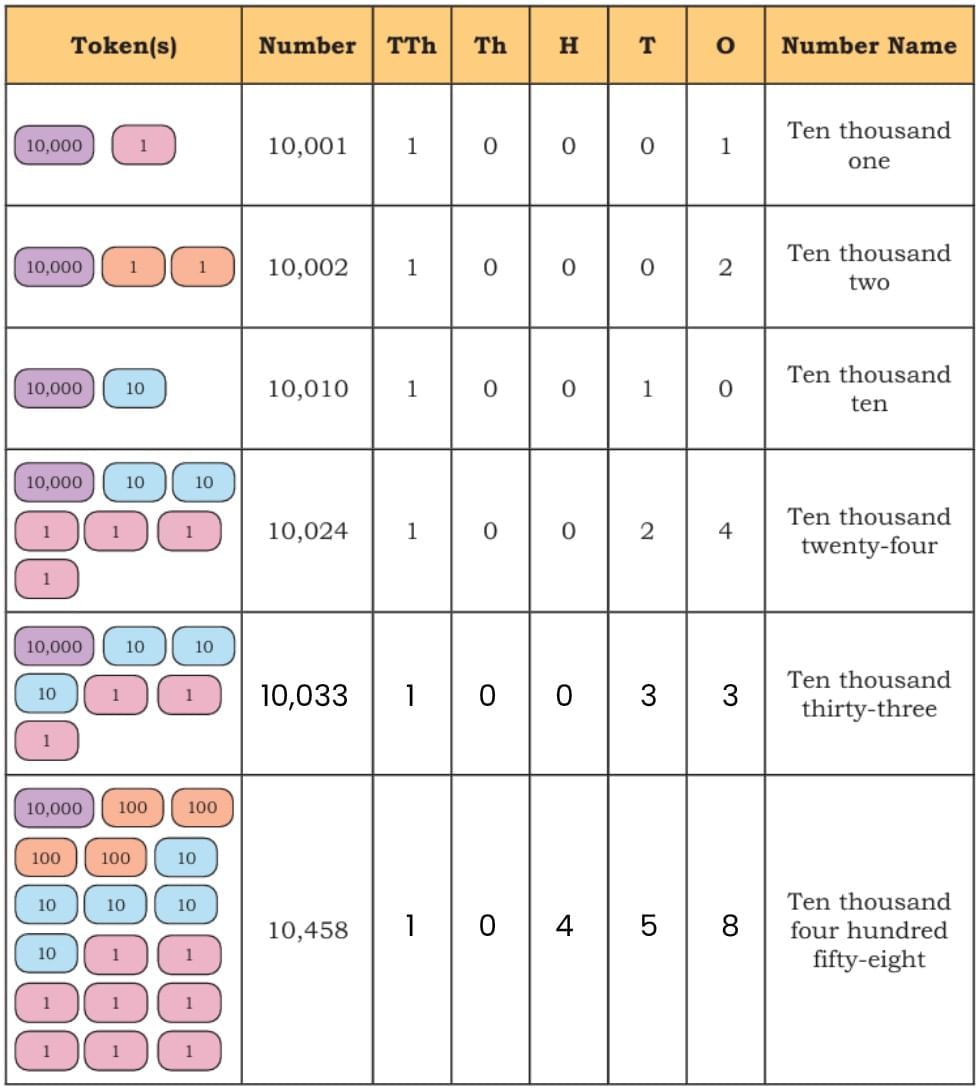
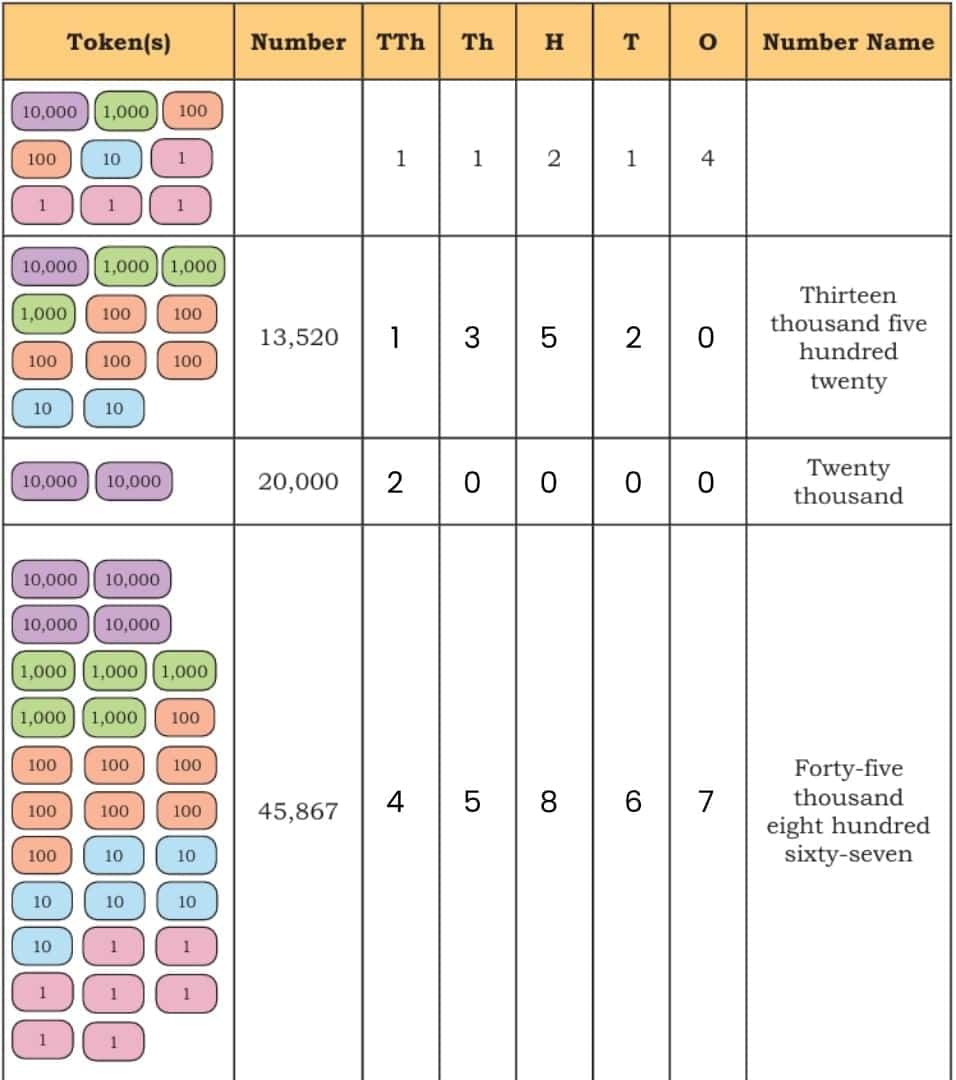
Nearest Tens (10s), Hundreds (100s), and Thousands (1,000s)
Imagine a rabbit trying to find its food! The rabbit needs to go to the nearest place where its food is kept.
Let’s help a rabbit find its food by understanding how to round numbers to the nearest tens, hundreds, and thousands.
Part 1: Nearest Tens of 2,346
Situation:
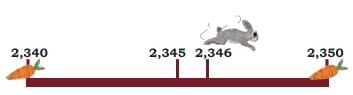
- The rabbit is standing at 2,346.
- The food is kept at the neighbouring tens — these are the numbers that are 10 apart from 2,346.
- The two closest tens are:
- 2,340 (just before 2,346)
- 2,350 (just after 2,346)
What to do:
We check which one is closer to 2,346.
- From 2,346 to 2,340: 6 jumps back
- From 2,346 to 2,350: 4 jumps forward
Answer:
- 2,350 is the nearest ten to 2,346
- It will need 4 jumps to reach 2,350
Part 2: Nearest Hundreds of 2,346
Situation:

- The rabbit is still at 2,346
- The food is now kept at neighbouring hundreds
- The two closest hundreds are:
- 2,300
- 2,400
What to do:
We check which one is closer to 2,346.
- From 2,346 to 2,300: 46 jumps back
- From 2,346 to 2,400: 54 jumps forward
Answer:
- 2,300 is the nearest hundred to 2,346
- It will need 46 jumps to reach 2,300
Part 3: Nearest Thousands of 2,346
Situation:
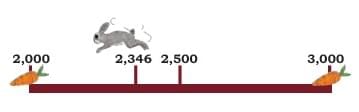
- The rabbit is still at 2,346
- The food is now kept at neighbouring thousands
- The two closest thousands are:
- 2,000
- 3,000
What to do:
We check which one is closer to 2,346.
- From 2,346 to 2,000: 346 jumps back
- From 2,346 to 3,000: 654 jumps forward
Answer:
- 2,000 is the nearest thousand to 2,346
- It will need 346 jumps to reach 2,000
Travelling, Now and Then

Means of Transport
- We learnt that people in the past travelled on foot, on animals, and used boats and sailing ships.
- The animals that have been used for travelling include bullocks, horses, donkeys, mules, and elephants.
- In hilly and snow-covered regions, yaks, dogs, and reindeers have been used, while camels have been used in deserts.
- Now, people use bicycles, motorbikes, cars, buses, trains, ships, and aeroplanes to travel from one place to another.
- Submarines are used to go deep under water.
- Humans are also using spacecraft to travel to outer space.
In an hour a person can generally travel:
- On foot: 3 – 5 km
- On horseback: 10 – 15 km
- By cycle: 12 – 20 km
- By motorbike: 40 – 60 km
- By train: 40 – 160 km
- By ship: 25 – 45 km
- By aircraft: 750 – 920 km
- By spacecraft: minimum 28,000 km
Finding Large Numbers Around Us
We saw that the distance (in kilometre) covered by different means of transport in an hour can range from a 1-digit number to a 5-digit number.
Can we find other contexts around us that contain numbers in this range?
Let us consider the situation below.
- A book has around 200 pages, and each page has about 50 words.
- The book therefore has about 10,000 words in all.
Usually, we measure distances in sea and air using nautical miles. For now, we will use 1 km = 1,000 m. By now, you know different units of measuring length. We will study the units for measuring length, kilometre, in detail in a later chapter.
Pastime Mathematics
Math can be fun, even when you are just passing time! Here are some puzzles that involve numbers and logical thinking.
The River Crossing Puzzle

Sanju & Mira in a trainSanju and Mira are sitting in a train. They want to have fun, so they start playing games. Mira gives Sanju a puzzle called the “river crossing puzzle”.
The Puzzle
There is a boatman who wants to cross a river using a small boat.
He has three things with him:

Boatman
- A lion
- A sheep
- A bundle of grass
The boat is very small. It can carry only one thing at a time with the boatman.
But there are two problems:
- If the sheep and grass are left alone on the riverbank, the sheep will eat the grass.
- If the lion and sheep are left alone on the riverbank, the lion will eat the sheep.
So the boatman has to be very careful about what he leaves behind when he takes something across.
Goal
Help the boatman take all three — the lion, the sheep, and the grass — to the other side of the river safely.
No one should get eaten, and he should do it in the least number of trips.
Step-by-Step Solution
Let’s go step by step:
First Trip:
The boatman takes the sheep across the river and leaves it on the other side.
Now:
- Other side: Sheep
- Starting side: Lion, Grass
- Nothing gets eaten
Second Trip:
He comes back alone and then takes the lion across the river.
But this time, he does not leave the lion.
Instead, he brings the sheep back with him.
Now:
- Other side: Lion
- Starting side: Grass
- Boat: Boatman and Sheep
Third Trip:
He drops the sheep back on the starting side and takes the grass across the river.
Now:
- Other side: Lion and Grass
- Starting side: Sheep
Fourth Trip:
He comes back alone and finally takes the sheep across.
Final Result
All three — lion, sheep, and grass — are safely on the other side.
No one got eaten.
It took the boatman 7 trips total:
- 4 trips with passengers
- 3 trips coming back alone or with the sheep
Pile of Pebbles Game
Sanju and Mira are still traveling on the train. Now Sanju teaches Mira a new game called the “Pile of Pebbles.”

How to Play the Game
- There are two piles of pebbles.
- Each pile has 7 pebbles at the beginning.
Rules of the Game:
- Two players take turns.
- On your turn, you can pick any number of pebbles (1 or more) but only from one pile.
- You cannot pick pebbles from both piles in the same turn.
- The player who picks the last pebble — that is, there are no pebbles left in both piles after their move — wins the game.
What’s the Challenge?
Mira asks: “How can I make sure I win this game?”
Sanju tells her: “Try playing the game with smaller numbers of pebbles, like 1 in each pile, then 2 in each pile, and so on. Look for a pattern to find a winning strategy.”
Let’s Try Small Examples First
Example 1: 1 pebble in each pile (1, 1)
- Player 1 takes all the pebbles from one pile.
- Player 2 takes the last pebble from the other pile — and wins.
- So, if it starts at (1, 1), the second player wins.
Example 2: 2 pebbles in each pile (2, 2)
- Player 1 takes 2 from one pile → (0, 2)
- Player 2 takes 2 from the other pile → (0, 0) → Player 2 wins again
Again, (2, 2) is a losing position for the first player.
Example 3: 3 in each pile (3, 3)
- Same pattern continues. If both piles are equal, the second player can always copy what the first player does, and win.
What Pattern Do We See?
- If the two piles have the same number of pebbles, then the second player can always win by copying the first player’s moves.
- But if the two piles have different numbers, then the first player can win if they know what to do.
Winning Strategy
To win the game:
- Try to leave the piles in a position where both piles have the same number of pebbles for your opponent.
- Then, whatever number they take from one pile, you take the same number from the other pile.
- Keep copying their move until you get the last pebble.
In Our Case (7, 7)
- The game starts with 7 pebbles in each pile.
- If you go second, you can win by copying your opponent’s moves.
- If you go first, you should try to make the piles equal after your move, so the second player cannot copy you and win.
The Number Puzzle
Now it’s Mira’s turn to give a puzzle to Sanju.
She gives him a fun number puzzle that looks simple at first, but has an amazing surprise in the end.
How to Play the Puzzle
Let’s understand the steps clearly:
Step 1:
Pick any two different digits.
For example: 3 and 7
Step 2:
Make two 2-digit numbers using those digits.
You can make:
- 37 (3 first, 7 second)
- 73 (7 first, 3 second)
Step 3:
Subtract the smaller number from the bigger number.
Here:
73 – 37 = 36
Step 4:
Now use the two digits of the result (which is 3 and 6)
and repeat Steps 2 and 3.
Let’s do it:
- 36 and 63
- 63 – 36 = 27
Use 2 and 7 now:
- 27 and 72
- 72 – 27 = 45
Use 4 and 5:
- 45 and 54
- 54 – 45 = 9
Now we got a single-digit number — 9.
Mira’s Surprise
Mira says:
“No matter which two digits you start with, you will always end up with 9.”
The whole process will look as shown below.

This makes the puzzle magical and fun. But how did she know that?
Let’s Explore the Pattern
Let’s take a closer look at the examples:
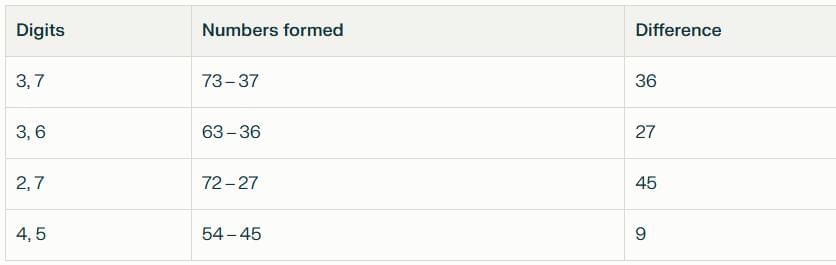
Look at the differences:
36 → 27 → 45 → 9
Each time, we use the digits from the result and continue.
Eventually, we reach 9, a single-digit number.
Try with Other Digits
Let’s try starting with 1 and 9:
- 91 – 19 = 72
- Use 7 and 2 → 72 – 27 = 45
- Use 5 and 4 → 54 – 45 = 9
Again, we get 9.
What’s the Trick or Pattern?
Look at this:
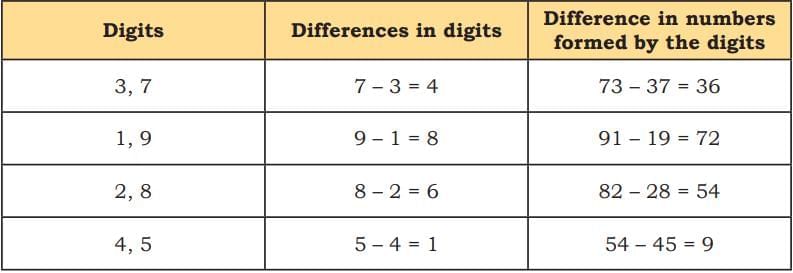
Now look at the relationship:
- 36 ÷ 4 = 9
- 72 ÷ 8 = 9
- 54 ÷ 6 = 9
- 9 ÷ 1 = 9
So, the difference between the two numbers is always a multiple of 9.
That’s how Mira knew that the process will always end at 9.
Try This Yourself
Try different starting digits and make your own table:
- Choose digits so that the difference between the numbers is 2, 3, 5, or 7.
- See what pairs of digits give you 9 in just one or two steps.
- See which pairs take the longest time (most steps) to reach 9.
King’s Horses
There was once a king who loved horses a lot. He had 20 beautiful horses. The king kept his horses in a big building called a stable. There, a man called a caretaker took care of the horses for the king.
One day, a thief sneaked in at night and stole one horse! Now there were only 19 horses left. The caretaker was scared that the king would be angry if he found out a horse was missing.
So, the clever caretaker tried to trick the king! He arranged the horses in a way so that when the king looked, he saw 5 horses on each side of the stables, and there are 4 sides. The king counted: 5 on this side, 5 on that side, 5 on another, and 5 on the last, which makes 20 horses. The king thought all the horses were there and went away happy.
But there really weren’t 20 horses left!
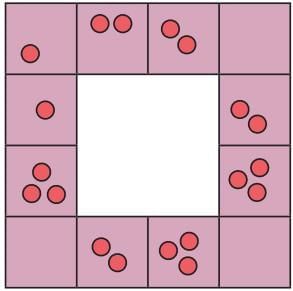
If you count the horses one by one, you’ll see there are only 19 horses. So, what was the caretaker’s trick?
Here’s the trick:
The caretaker put some horses at the corners of the square. These corner horses are counted on both sides — for both sides they are on! For example, if there’s a horse in the left corner, you might count it for the left and the top sides.
So, the king was counting the same horse twice for two sides!
The next night, the thief came again and took one more horse. Now only 18 horses were left. The caretaker moved the horses again, so the king saw 5 horses on each side the next day.