Introduction
A quilt is made by joining pieces of cloth together, often in different shapes and sizes. To decorate or cover it, we need to know the length around it and the space it covers. In this chapter, we learn to find the perimeter and area of shapes and use them in real-life situations like measuring quilts, floors, and gardens.

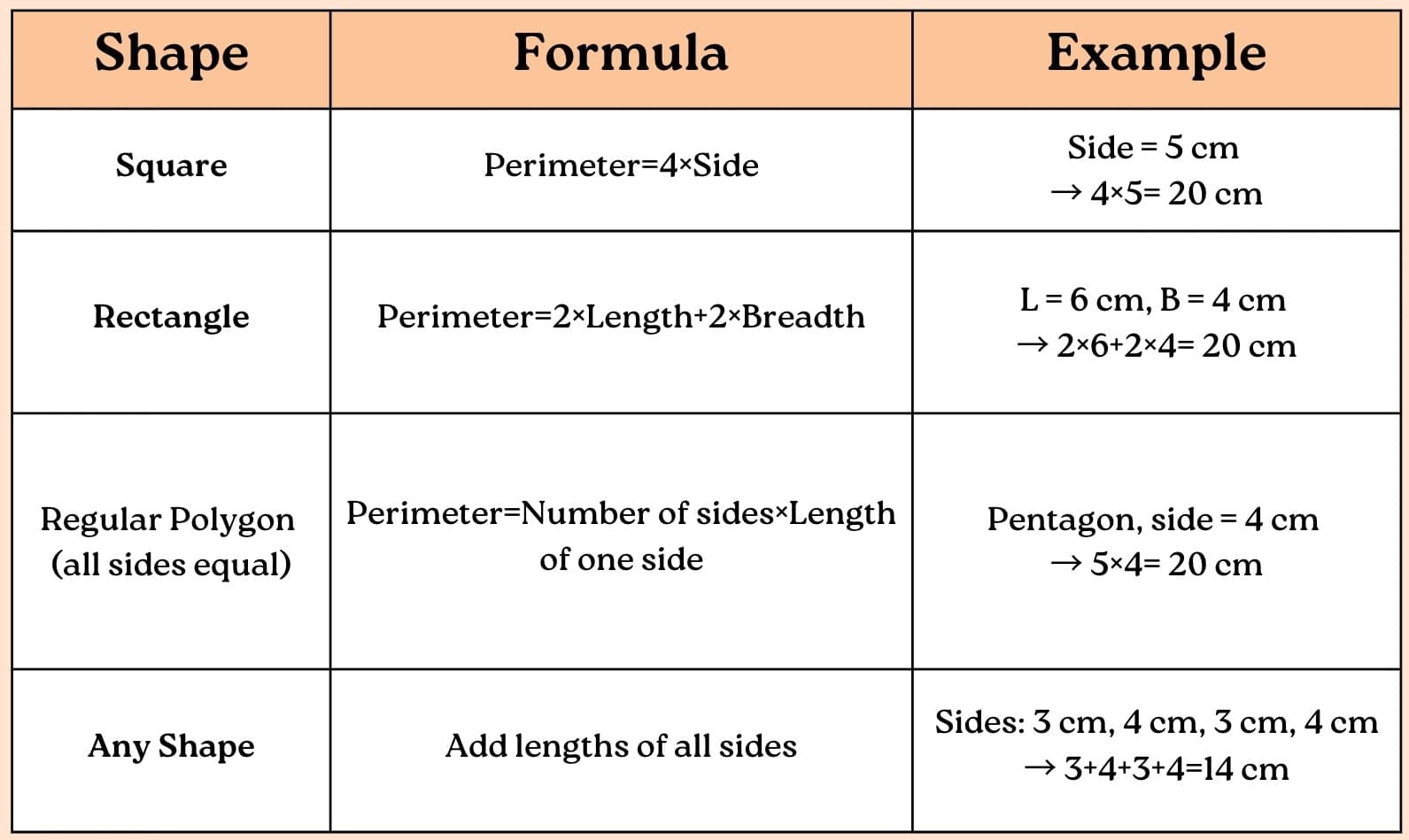
Perimeter
Preetha and Adrit’s grandmother made a beautiful quilt cover from old clothes and now wants to decorate it with lace along its border, using two different colours. To know how much lace of each colour she needs, we must remember that the length around a shape is called its perimeter. Here, we learn how to find the perimeter of different shapes and use it in real-life situations like decorating and designing.
Meaning:
The perimeter is the total distance around a shape. Imagine you are walking along the edge of a garden, a playground, or a quilt — the total distance you walk is its perimeter.
How to Find Perimeter:
Remember:
- Write units for perimeter (cm, m, km).
- The perimeter tells us the length around and not about the inside.
Try yourself:
What is the perimeter?
- A.The total distance around a shape
- B.The weight of a shape
- C.The area inside a shape
- D.The height of a shape
View Solution
Now that we know how to measure the length around a shape, let’s think about how much space a shape covers inside.
Preetha and Adrit’s grandmother is making a rug with square patches. Look at the picture of the rug – can you count how many patches she has used? Each patch takes up some space, and all the patches together cover the whole rug.
Preetha and Adrit also tried covering their table using different shapes:
- Preetha used triangles and circles.
- Adrit used squares and rectangles.

They found that triangle, square and rectangle shapes cover the top of the table without gaps and overlaps. Circle shape leaves gaps.
TWENTY triangles cover Table 1.
EIGHT squares cover Table 3.
SIX rectangles cover Table 4
The region covered by the triangles, squares or rectangles is called the area of the table. To find the area of a region, we usually fill it with shapes that tile well — like squares, rectangles, and triangles. Circles do not tile perfectly because they leave spaces in between. Let us learn about area in detail:
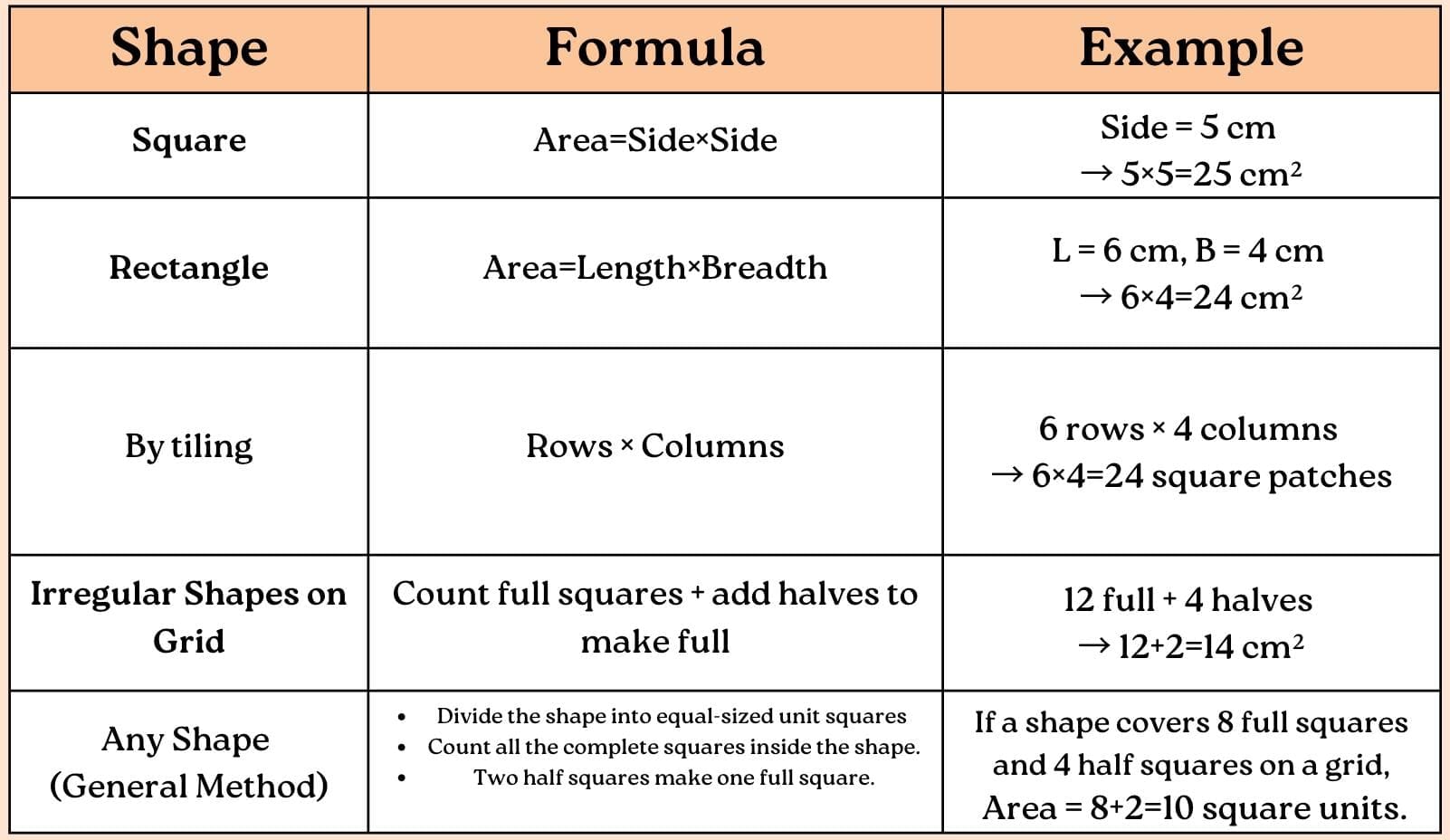
Area
Meaning:
The area of a shape is the amount of surface it covers inside its boundary. If you spread tiles, patches, or paper inside a shape until it’s filled, the space covered is the area.
How to Find Area:
Remember:
- Write units for area (cm², m², km²).
- The area tells us the space inside a shape, not the length around it.
Let us look at the following examples:
1. Preetha is playing with tiles. She covers her desk with different shapes, as shown below. Look at the different tiles on her desk and answer how many of the following shapes will cover the desk.
(a) Green triangles __________
(b) Red triangles __________
(c) Blue squares __________
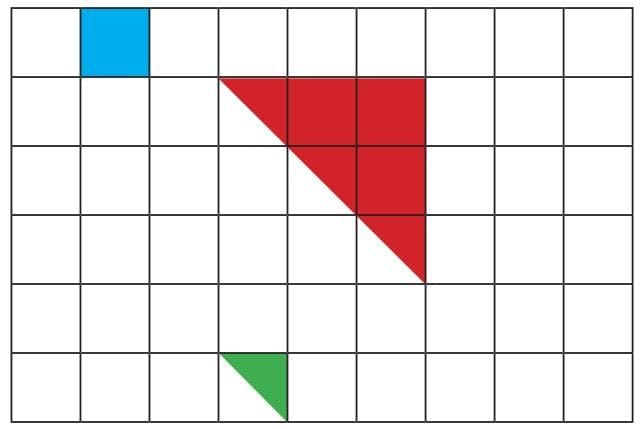
Ans: (a) Green triangles = 1
(b) Red triangles = 4
(c) Blue squares = 1
2. Compare the areas of the two gardens given below on the square grid. Share your observations.
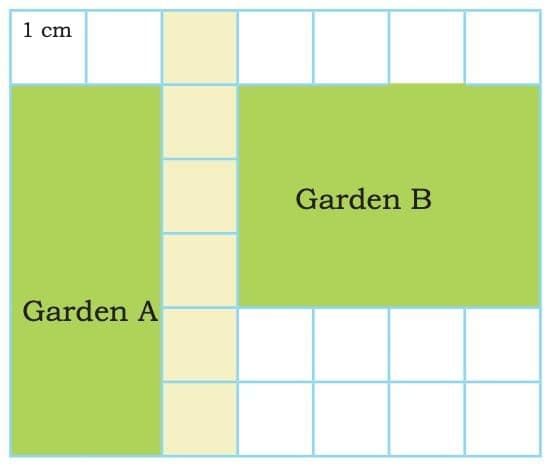
Area of Garden A = _____ cm square
Area of Garden B = _____ cm square
Ans: Area of Garden A = 12 cm²
Area of Garden B = 12 cm²
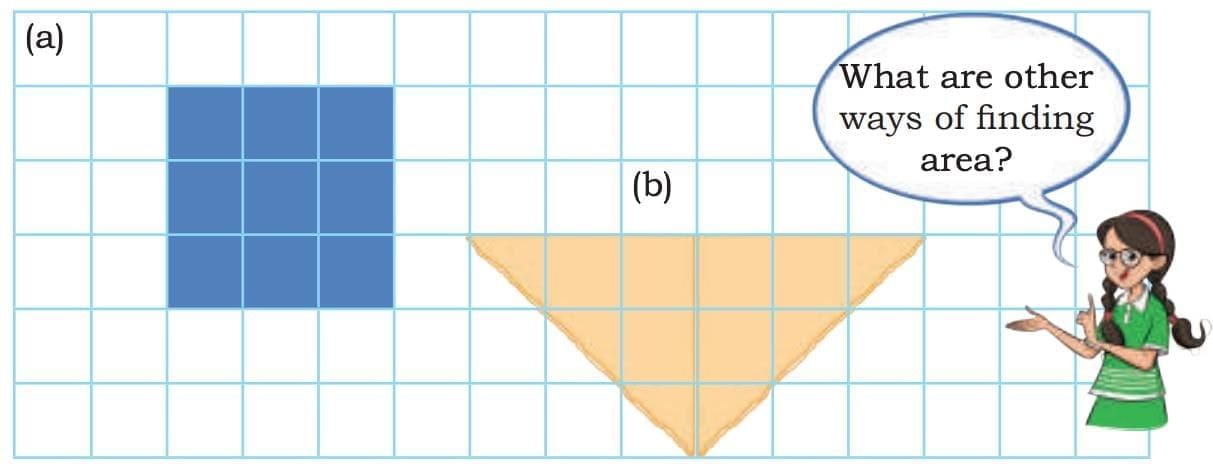
3. Is the area of shape (a) less than the area of shape (b) given below? Discuss.
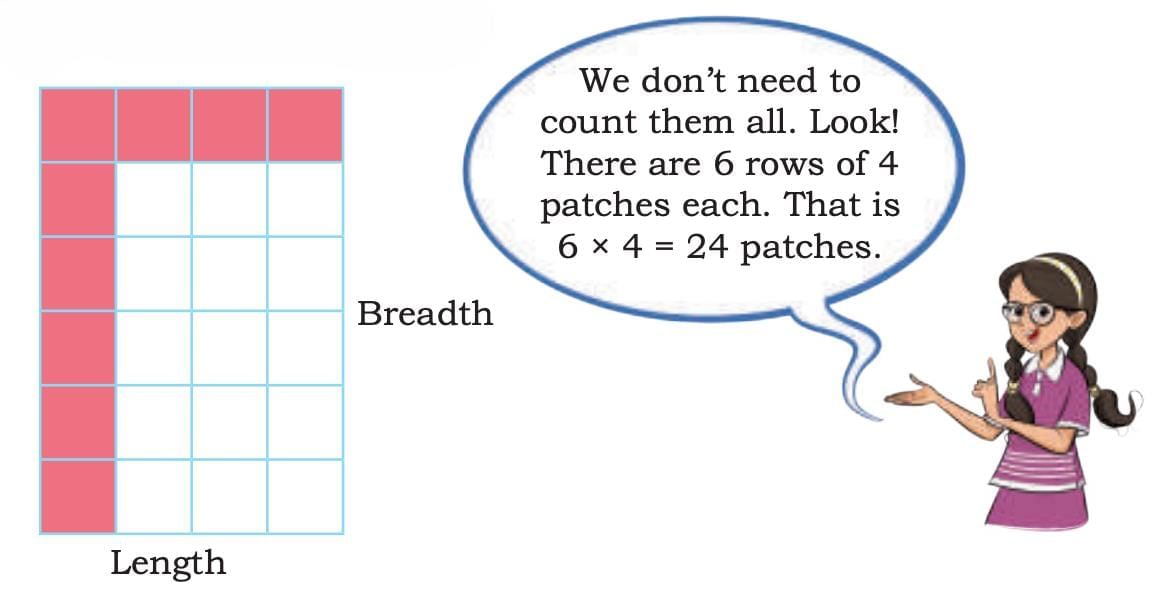
Preetha and Adrit’s grandmother is making another square patchwork. She arranges the patches as shown below. Can you guess how many patches she will need? How did you find it?
Did you notice that 6 is the length of one side and 4 is the length of the non-equal side of the rectangle?
Ans: Yes, the area of shape (a) is less than the area of shape (b) because shape (b) covers more square units on the grid.
For the square patchwork, there are 6 rows with 4 patches in each row.
Total patches = (6×4) square cm=24 square cm
Here, 6 is the length and 4 is the breadth of the rectangle, showing that:
Area of a Rectangle = Length × Breadth
Similarly, we can also find the perimeter of the rectangular shape.
Perimeter = Length + Length +Breadth + Breadth
= 2 × Length + 2 × Breadth
Have you ever wondered what would happen if all the sides of a rectangle were equal, that is, the case of a square?

Let us think about a square whose sides are 5 units long.

Conclusion:
In this chapter, we learned how to find the perimeter (the length around a shape) and the area (the space inside a shape). We saw how to measure them for squares, rectangles, and other shapes using unit squares, counting patches, and formulas. We also learned that some shapes can cover a surface without leaving gaps, and that two shapes can have the same area but look different. Knowing how to find perimeter and area helps us in real life, like decorating quilts, measuring gardens, or tiling floors.