Introduction
In this chapter, we will learn about factors and multiples and how they are related. A factor divides a number exactly, like 2 is a factor of 8 because 8 ÷ 2 = 4 with no remainder. A multiple is what you get when you multiply a number by a whole number, like the multiples of 3 are 3, 6, 9, 12, and so on. We will also explore common factors (factors shared by two or more numbers), common multiples (multiples shared by two or more numbers), and prime numbers (numbers that have only two factors: 1 and itself).What is a Factor?
A factor of a number is a number that can divide it completely without leaving any remainder.
Example:
Factors of 8 are numbers that divide 8 exactly:
- 1 divides 8 exactly (8 ÷ 1 = 8)
- 2 divides 8 exactly (8 ÷ 2 = 4)
- 4 divides 8 exactly (8 ÷ 4 = 2)
- 8 divides 8 exactly (8 ÷ 8 = 1)
So, the factors of 8 are 1, 2, 4, and 8.
How to find factors?
- Start with the number 1 and go up to the number itself.
- Divide the number by each one.
- If the division has no remainder, then that number is a factor.
Common Factors
When two or more numbers share the same factor, that factor is called a common factor.
Example:
Find common factors of 12 and 18.
- Factors of 12: 1, 2, 3, 4, 6, 12
- Factors of 18: 1, 2, 3, 6, 9, 18
Common factors are the numbers that appear in both lists: 1, 2, 3, and 6.
How to find Common Factors?
- Find all factors of the first number.
- Find all factors of the second number.
- See which factors appear in both lists.
Example 1:
Sometimes, numbers are created by multiplying another number by the same value each time. If we know the final numbers, we can work backwards to find the multiplier. This also teaches us about common factors— numbers that can divide all given numbers exactly.
Imagine a magic box. You put a number inside, the box multiplies it by a fixed number, and the result appears. In this activity, the numbers coming out of the box are 28, 36, 48, and 72.
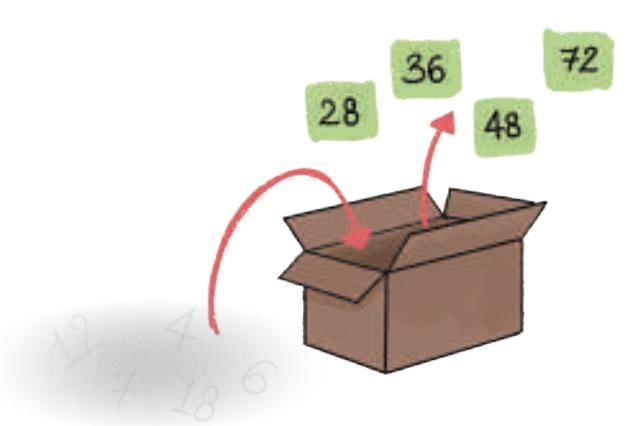
We ask:
(a) What could the multiplier be?
(b) Could there be more than one multiplier?
(c) What numbers might have been inside the box?
To solve this, we find numbers that divide all four outputs exactly. These are common factors.
(a) The multiplier could be 1, 2, or 4 because all the numbers 28, 36, 48, and 72 can be divided evenly by these numbers.
(b) Yes, there could be more than one multiplier. For example, if the multiplier were 2, the inside numbers would be half of the given numbers. If it were 4, the inside numbers would be one-fourth of them.
(c) The numbers that might have been inside the box depend on the multiplier:
- If multiplier is 2 → inside numbers: 14, 18, 24, 36
- If multiplier is 4 → inside numbers: 7, 9, 12, 18
- If multiplier is 1 → inside numbers: 28, 36, 48, 72
This shows that the same output can come from different possible multipliers.
This activity shows that there can be more than one possible multiplier. It also helps us see that factors divide numbers exactly, while multiples are numbers made by multiplying. The same set of numbers can be made in different ways by choosing different multipliers.How to Identify Factors Using Arrays (Pairs)
A factor pair of a number is two numbers that multiply together to give that number.
For example, for 12:
- 1 × 12 = 12
- 2 × 6 = 12
- 3 × 4 = 12
So, the factors are 1, 2, 3, 4, 6, and 12.
If you try to arrange objects (like dots or blocks) in rows and columns, the number of rows and columns form factor pairs.Example 2:
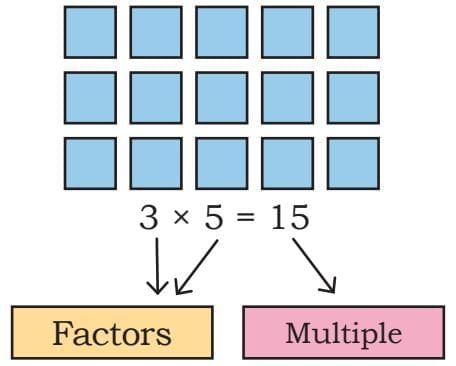
One way to find the factors of a number is by arranging objects into arrays – rows and columns. Each arrangement shows a pair of factors that multiply to make the number.
Here, we see the number 15 can be arranged as 3 rows of 5. This tells us 3 × 5 = 15, so 3 and 5 are factors of 15. This can be seen in the following figure:

Similarly, the number 12 can be arranged as 3 × 4, 2 × 6, and 1 × 12. This tells us its factors are 1, 2, 3, 4, 6, and 12. This can be seen in the following figure:
Students, now try making arrays for numbers like 10, 14, 20, 25, and 32.
Try yourself:What are the factors of 24?
- A.1, 2, 3, 6, 12, 24
- B.1, 2, 3, 4, 6, 8, 12, 24
- C.2, 3, 4, 6, 8, 12
- D.1, 2, 4, 6, 8, 24
View SolutionPrime and Composite Numbers
Some numbers are called prime numbers because they have only two factors: 1 and the number itself. For example, 5 is prime because only 1 and 5 divide it exactly.
Other numbers have more than two factors; these are called composite numbers. For example, 12 is a composite number because it has many factors like 1, 2, 3, 4, 6, and 12.

Understanding the difference between prime and composite numbers helps us learn more about how numbers work:
Arrays make it easy to see all the factor pairs of a number. They also help us quickly identify prime numbers, which have only two factors – 1 and the number itself.What is a Multiple?
A multiple of a number is what you get when you multiply that number by any whole number.
Example:
Multiples of 3 are:
- 3 × 1 = 3
- 3 × 2 = 6
- 3 × 3 = 9
- 3 × 4 = 12
- and so on…
So, the multiples of 3 are 3, 6, 9, 12, 15, 18, …
How to find multiples?
Multiply the number by 1, 2, 3, 4, etc., and list the answers.Common Multiples
When two or more numbers share the same multiple, that multiple is called a common multiple.
Example:
Find common multiples of 3 and 4.
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, …
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, …
Common multiples are: 12, 24, 36, …
How to find common multiples?
- Write down multiples of the first number.
- Write down multiples of the second number.
- See which multiples appear in both lists.
Least Common Multiple (LCM)
The Least Common Multiple or LCM is the smallest number that is a multiple of two or more numbers.
In the example above, the smallest common multiple of 3 and 4 is 12.
How to find an LCM:
- List the multiples of each number.
- Identify the common multiples from the lists.
- Choose the smallest common multiple.
- That smallest common multiple is the LCM.
Example 3:
One sunny morning in the forest, Rabbit and Frog decided to have a jumping race. They both started from the same tree stump at position 0 on a long number line painted on the forest floor. Rabbit was fast but liked to take big leaps — 4 steps at a time. The frog was smaller but very quick, jumping 3 steps at a time.

Rabbit began: 0, 4, 8, 12, 16, 20, 24…
Frog began: 0, 3, 6, 9, 12, 15, 18, 21, 24…
As they hopped along, something interesting happened — they both landed on 12 at the same time! That was their first meeting point. After that, they met again at 24, then 36, and then 48.
The forest owl explained, “These meeting points are called common multiples — numbers that are in both the Rabbit’s list of multiples and the Frog’s list. The first one, where you meet, is called the Least Common Multiple, or LCM.”
Common multiples are numbers that appear in the multiplication tables of both numbers. The smallest one is the LCM, and all other common multiples are multiples of the LCM. When two jump patterns meet, the numbers they land on together are common multiples. Here, Rabbit and Frog’s LCM is 12, so all their common multiples are multiples of 12.
Example 4:
One bright morning, a spider and a grasshopper decided to practise jumping together on the number line.
The spider was small but quick, hopping 3 steps each time: 0,3,6,9,12……
The grasshopper was stronger and leapt 6 steps each time: 0,6,12,24……
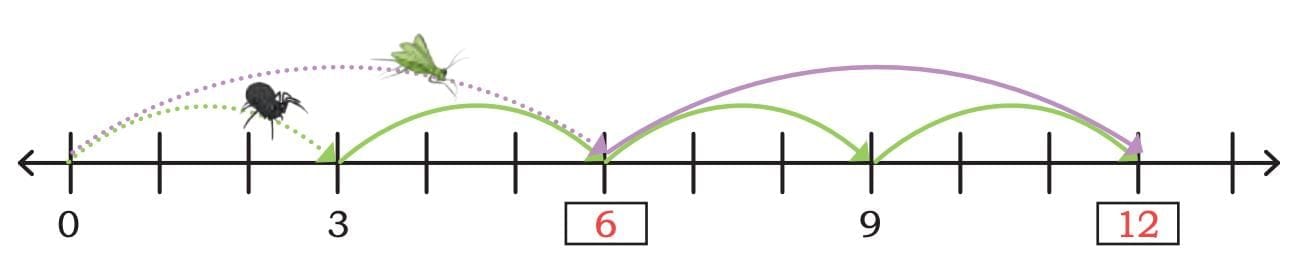
As they hopped along, they noticed something interesting — they both landed on 6 at the same time. That was their first meeting point. After that, they met again at 12, then 18, then 24, and so on.
The forest parrot explained, “The numbers where you both land together are called common multiples — numbers that appear in both your jumping lists. The first number where you meet is called the Least Common Multiple (LCM).”
In this case, because 6 is already a multiple of 3, every time the grasshopper lands, the spider lands there too. So all the grasshopper’s numbers are also common multiples. The smallest of these, 6, is the LCM of 3 and 6.
Common multiples are numbers that appear in the multiplication tables of both numbers. If one number is a multiple of the other, the larger one becomes the LCM. For jumps of 3 and 6, the common multiples are 6, 12, 18, 24, …, and the LCM is 6. When one number is a multiple of the other, the common multiples are just the multiples of the bigger number.Example 5:
Mowgli was walking along a forest trail where his friends lived at different numbered spots. Starting from 0, he decided to visit his friends by jumping 2 steps at a time.
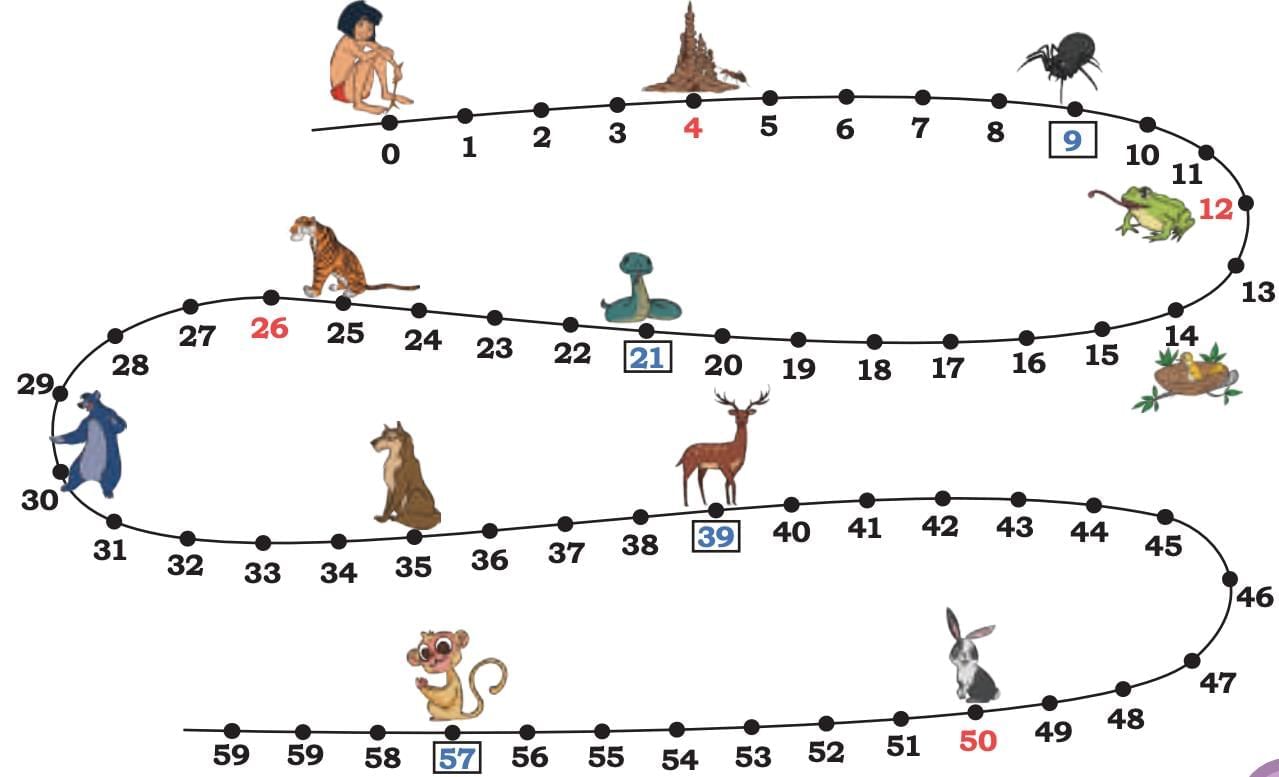
His jumps went like this: 0,2,4,6,8,10,12,14,16,18……
Looking at the positions on the trail, Mowgli realised he could meet:
- The ant at position 4
- The frog at position 12
- The bird at position 14
- The rabbit at position 50
All of these numbers can be divided exactly by 2. This means 2 is a common factor for all these positions — they are all multiples of 2.
When you take jumps of the same size and land on certain numbers, that jump size is a factor of all those numbers. If the same jump works for multiple positions, that number is their common factor. Jumping by 2 steps lets Mowgli meet all friends whose house numbers are multiples of 2. This shows that 2 is a common factor of those numbers.
Try yourself:Which of the following lists shows the first five multiples of 15?
- A.15, 25, 35, 45, 55
- B.10, 20, 30, 40, 50
- C.15, 30, 45, 60, 75
- D.1, 3, 5, 15, 30
View SolutionHow to Use Factors and Multiples?
- Factors help us divide or break numbers apart.
- Multiples help us build numbers up by repeated addition or multiplication.
- Common factors and multiples help us solve problems like sharing things equally, finding common timings for events, or arranging objects neatly.
Conclusion
In this chapter, we learned about factors and multiples, two important ideas in numbers. A factor is a number that divides another number exactly without leaving any remainder. Multiples are numbers we get when we multiply a number by whole numbers like 1, 2, 3, and so on. Some numbers share factors, which we call common factors, and some share multiples, called common multiples. The smallest common multiple of two numbers is called the Least Common Multiple or LCM. We also learned about prime numbers, which are special numbers that have only two factors: 1 and themselves. Understanding factors and multiples helps us solve many math problems and real-life situations like sharing things equally and finding common timings.