Introduction
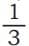
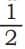
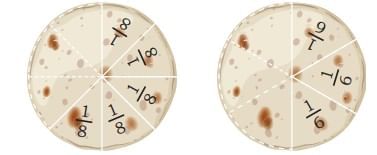
Tamanna is a student of Grade 5. She has two chocolates of different sizes. She says that of chocolate 1 is bigger than of the chocolate 2.


Chocolate 1 Chocolate 2
Is that correct?
We can see that chocolate 2 is alot bigger than chocolate 1, they are of different sizes, so we cant really compare them both
Let’s learn about fractions to understand this!
- When we compare fractions, we need to make sure the chocolates (wholes) are the same size.
- If Tamanna’s chocolates are different sizes, then
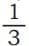 of a bigger chocolate can indeed be larger than
of a bigger chocolate can indeed be larger than 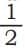 of a smaller chocolate!
of a smaller chocolate!
To compare two fractions of two wholes, the wholes from which the fractions are made must be the same.
Playing with a Grid
Let’s understand fractions by shading grids. This activity helps us visualise what fractions look like:
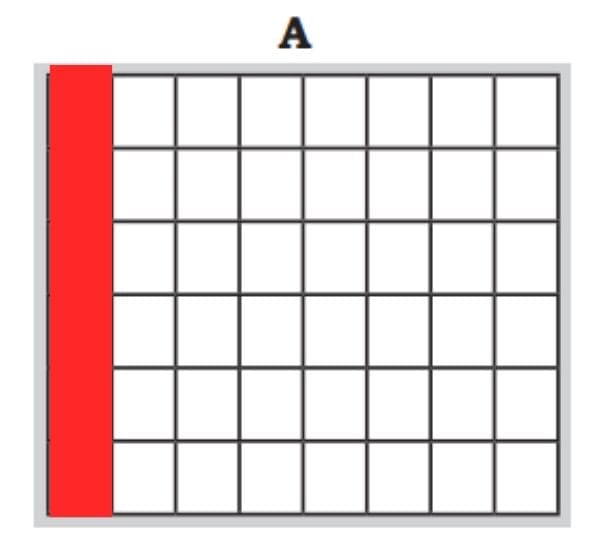
Grid A:

- Total squares = 48
- Shade 1/8 in red (shade 1 square out of 8)
- This means we divide the grid into 8 equal parts and colour 1 part
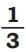
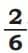
Understanding Equivalent Fractions
Is equal to ?

In this picture we can see that, 2 parts out of 6 are shaded.
Now, lets divide the same picture in three equal parts

In this picture, we can see that, 1 part out of 3 is shaded.
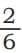
So, when we look at both the pictures showing the same shaded area, we can see that = . These are called equivalent fractions.
Equivalent fractions are fractions that represent the same part of a whole but are written differently.
Fun with Fraction Kit
Using a fraction kit helps us understand how fractions work. A fraction kit contains strips divided into equal parts.
Activity 1: Making a Whole
- How many 1/5 pieces do you need to make a whole? Answer: 5 pieces
- How many 1/8 pieces do you need to make a whole? Answer: 8 pieces
- How many 1/3 pieces do you need to make a whole? Answer: 3 pieces
Activity 2: Combining Different Pieces
- One piece of 1/2 and two pieces of 1/4 make a whole
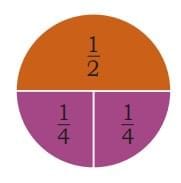
- This shows us: 1/2 + 1/4 + 1/4 = 1 whole
- Also: 1/2 = 2/4 (equivalent fractions)
Understanding the Pattern:
When a 1/2 piece is broken into 2 equal parts, each part becomes 1/4. So 2 pieces of 1/4 equal 1/2.
Lets see some more combinations:
- 1/3 + 1/3 + 1/3 = 1 whole
- 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 1 whole
- 1/4 + 1/4 = 1/2
Try yourself:
What do you need to make a whole using 1/5 pieces?
- A.3 pieces
- B.5 pieces
- C.8 pieces
- D.2 pieces
View Solution
Making Equivalent Fractions
What are Equivalent Fractions?
- Equivalent fractions are different fractions that show the same part of a whole.
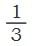
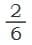
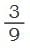
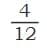 Example: , , , all represent the same amount even though they look different.
Example: , , , all represent the same amount even though they look different.- Sameer shaded one-third () of some shapes.
- When he split the shapes into smaller equal parts by drawing lines, he found fractions like:
- , , – all exactly cover the same shaded area as 1/3.
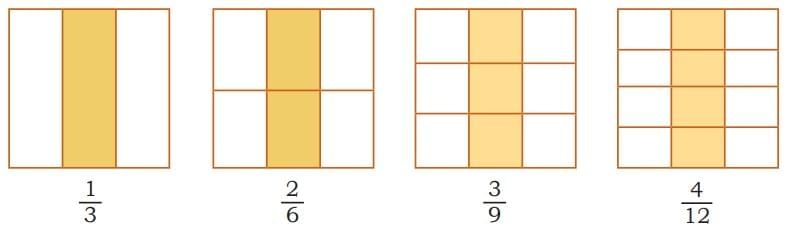
- This means = = =
- These are equivalent fractions.
How to check if two fractions are equivalent?
- If you multiply or divide both the top number (numerator) and the bottom number (denominator) of one fraction by the same number, you get an equivalent fraction.
- For example:
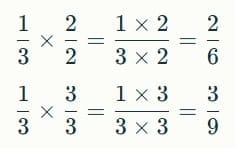
- In short, to get equivalent fractions, multiply or divide numerator and denominator by the same number.
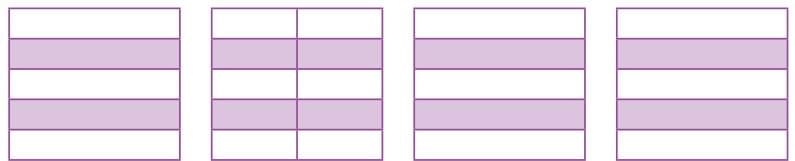
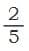 Look at figures showing shaded.
Look at figures showing shaded.
- Lets find equivalent fractions of using this:
- Multiply numerator and denominator by 2
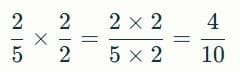
- Multiply numerator and denominator by 3:
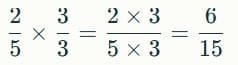
- Multiply numerator and denominator by 4:
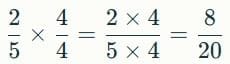
- These all represent the same part of the whole as .
When fractions have the same denominator (bottom number), we compare the numerators (top numbers). This is like comparing pieces of the same size.
Comparing Fractions—Same Denominator
- Fractions have two parts: numerator (top number) and denominator (bottom number).
- When fractions have the same denominator, it means the whole is divided into the same number of equal parts.
- To compare such fractions, we only need to look at the numerators.
Example: Sevi and Shami sharing a chikki

- The whole chikki is divided into 3 equal parts (denominator is 3).
- Sevi ate 1 part → 13
- Shami ate 2 parts → 23
- Since the denominator is the same (3), compare numerators:
- Numerator 1 (Sevi) and Numerator 2 (Shami)
- 2 is greater than 1, so
Shami ate more chikki than Sevi.
Comparing Fractions – Same Numerator
What does it mean to compare fractions with the same numerator?
- When fractions have the same numerator (same number of parts), but different denominators (different total parts), the bigger fraction is the one with the smaller denominator.
- This is because smaller parts make each piece bigger.
Example: Comparing who ate more paratha
- Suppose:
- You ate 13 paratha yesterday evening.
- Your friend ate 14 paratha yesterday evening.
- Both have the numerator 1 (one piece), but denominators are different (3 and 4).
- Since 3 is smaller than 4, 13 is bigger than 14.
- So, you ate more paratha than your friend.
Rule: When numerators are the same, the fraction with the smaller denominator is bigger.
Try yourself:
What do we compare when fractions have the same numerator?
- A.Values
- B.Denominators
- C.Sizes
- D.Numerators
View Solution
Fractions Greater Than 1
We know, a fraction tells us how many parts of a whole we have. For example, if a paratha (a soft flatbread) is cut into equal parts:
- 12 (one-half) means the paratha is cut into 2 equal parts, and you have one of those parts.
- 14(one-fourth or a quarter) means the paratha is cut into 4 equal parts, and you have one of those parts.
Sometimes, you can eat more than one whole paratha. This happens when you eat many pieces of paratha, so the total amount is more than one whole. This is called a “fraction greater than 1.”
Let’s see this with some examples.
Example 1: Eating Halves (12’s)
Imagine Raman’s father cuts parathas into halves (2 equal parts each).
- If Maa took 5 pieces of 12 paratha, how many whole parathas did she eat?
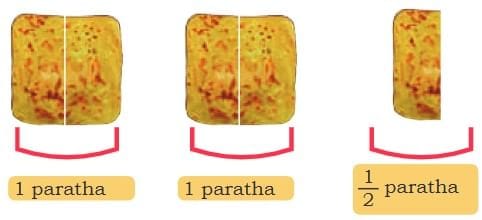
- Since 2 halves make 1 whole paratha, 5 halves are:
5×12=52=212 (which means 2 whole parathas and half of another one)
So, Maa ate 2 and a half parathas.
Using a Number Line to Understand
- If you draw a line and divide the space between 0 and 1 into 2 equal parts (because halves),
- Then each part is 12.
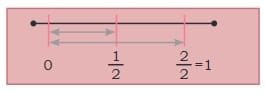
- Moving 5 steps of 12 along the line gets you to 2 and 12.

Example 2: Radhika’s halves
Radhika took 6 pieces of 12 paratha.

Number Line method
62=3 parathas
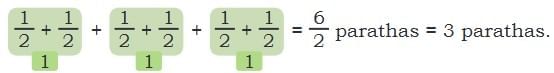
So, she ate 3 whole parathas.
- Dadiji took 7 pieces of 12 paratha = 72=312 parathas
- Raman ate 6 pieces of 12 paratha = 3 parathas
- Dadaji ate 7 pieces of 12 paratha = 3 and 12parathas
- Baba ate 5 pieces of 12 paratha = 2 and 12 parathas
To find how many parathas were made on that day, add all these fractions.
Now, some day, all parathas were cut into 4 pieces each (fourths).
- Dadaji took 9 pieces of 14 paratha. How many parathas did he eat
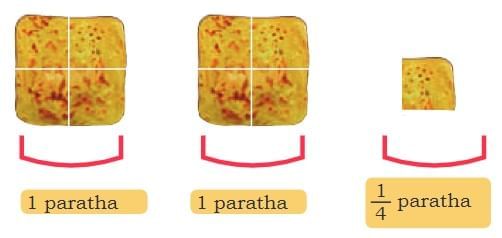
Since 4 fourths make 1 whole paratha, 9 pieces are:
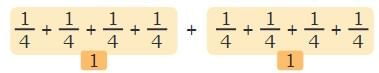
2 + 14
= 214
So, he ate 2 and one-fourth parathas.
Example 4: Sharing Pizzas
The family ordered 2 pizzas, and each pizza is cut into 3 equal slices.
- Total slices = 2 pizzas × 3 slices = 6 slices
- 6 family members need 1 slice each.
- Dadiji and Dadaji gave their slices to Raman.
- Maa and Baba gave theirs to Radhika.
That means:
- Raman gets his slice + 2 slices from Dadiji and Dadaji = 3 slices
- Radhika gets her slice + 2 slices from Maa and Baba = 3 slices

Each slice is:
13 (one slice out of 3)
So,
- Raman’s total pizza =
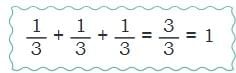
- Radhika’s total pizza =

When Raman gave 1 slice of pizza to Radhika

- Raman eats 2 slices = 2×13=23 pizza
- Radhika had 3 slices, now gets 1 more slice from Raman

Comparing Fractions With Reference to 1
Let us compare some more fractions. Between Sevi and Shami can you tell who ate less?


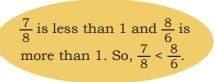
Comparing Fractions with Reference to 1/2


Who do you think ate more paratha?