3️⃣ A Story of Numbers – Short Notes

by

Reema’s Curiosity

Ancient civilizations needed numbers to:

  • Count food, livestock, trade goods, ritual offerings.
  • Track days and seasons.

Modern numbers evolved from ancient Indian concepts:

  • Yajurveda Samhita lists numbers by powers of 10:
    1 (eka), 10 (dasha), 100 (shata), 1000 (sahasra), 10,000 (āyuta), … up to 10¹².
  • Indian numerals (0–9) developed ~2000 years ago.
  • First instance in Bakhshali manuscript (3rd century CE) with 0 as a dot.
  • Aryabhata (499 CE) explained calculations using the Indian system.

Transmission of Indian numerals:

  • To Arab world (~800 CE) via Al-Khwārizmī (On the Calculation with Hindu Numerals, 825 CE) and Al-Kindi (On the Use of Hindu Numerals, 830 CE).
  • To Europe (~1100 CE) and popularised by Fibonacci (~1200 CE).
  • Called Arabic numerals in Europe; properly Hindu or Hindu-Arabic numerals.

Key Quote:
“The ingenious method of expressing every number using ten symbols with place value emerged in India.” — LaplaceMechanism of Counting

Purpose: To determine the size of a collection of objects (e.g., counting cows).Methods of Counting

  1. Objects
    • Use sticks, pebbles, or other tokens.
    • Each object represents one counted item (one-to-one mapping).
    • Example: 5 cows → 5 sticks.
  2. Sounds / Names
    • Map objects to spoken words, letters, or sounds.
    • Limited by the number of available symbols.
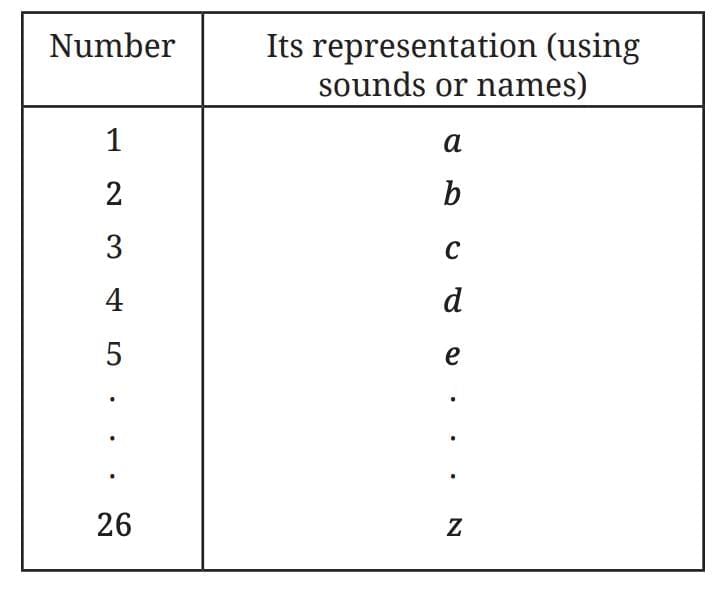    • Example: “a, b, c…”
  3. Written Symbols
    • Use a standard sequence of symbols to represent numbers.
    • This is an early form of written numbers.

Early Number SystemsI. Body Parts

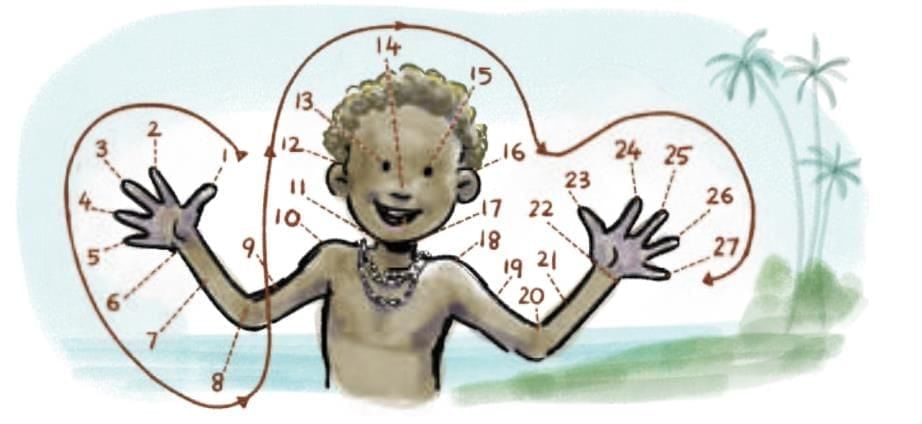  • Hands, fingers, body parts used to count (e.g., Papua New Guinea).

II. Tally Marks

  • Marks on bones/walls (e.g., Ishango bone, 20,000–35,000 years ago; Lebombo bone, 44,000 years ago).

III. Counting in Groups

  • Example: Gumulgal (Australia) counted in 2s:
    • 1 = urapon, 2 = ukasar, 3 = ukasar-urapon, 4 = ukasar-ukasar, …
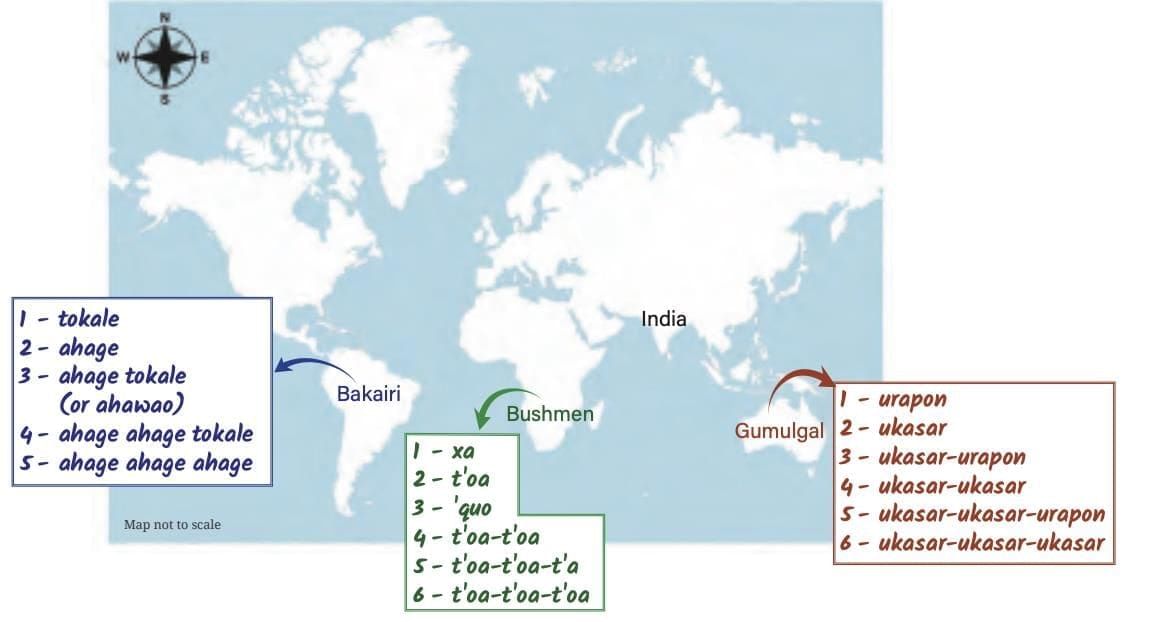  • Similar systems in South America & South Africa.
  • Advantage: Counting in groups reduces effort; precursor to grouping in larger systems (5s, 10s, 20s).

IV. Roman Numerals

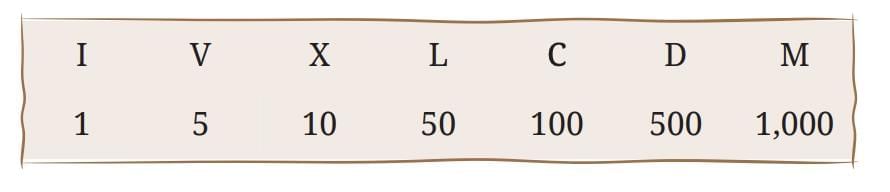  • Symbols: I (1), V (5), X (10), L (50), C (100), D (500), M (1000).
  • Numbers represented by sums of landmark numbers (e.g., 27 = XXVII).
  • Efficiency: Better than tally marks but difficult for arithmetic operations.
  • Use of abacus for calculations.

Concept of BaseI. Egyptian Number System

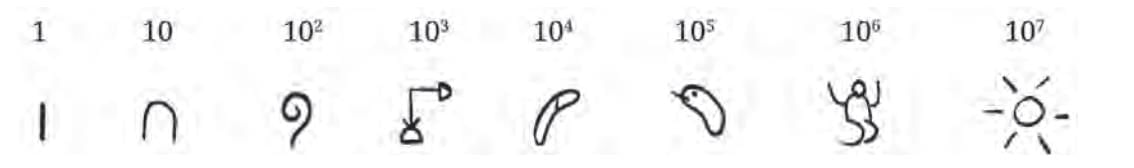  • Landmark numbers: 1, 10, 100, … (powers of 10, base-10 system).
  • Representation: Group numbers by landmark numbers starting from the largest.
  • Shortcomings: Requires new symbols for higher powers of 10.

II. Base-n Systems

  • Landmark numbers: 1, n, n², n³, …
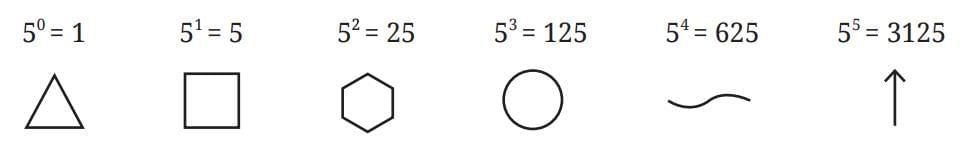  • Example: Base-5 system → 1, 5, 25, 125, …
  • Advantages: Simplifies addition and multiplication; product of landmark numbers is another landmark number.

III. Abacus

  • Early calculation tool using base-10 grouping of numbers.
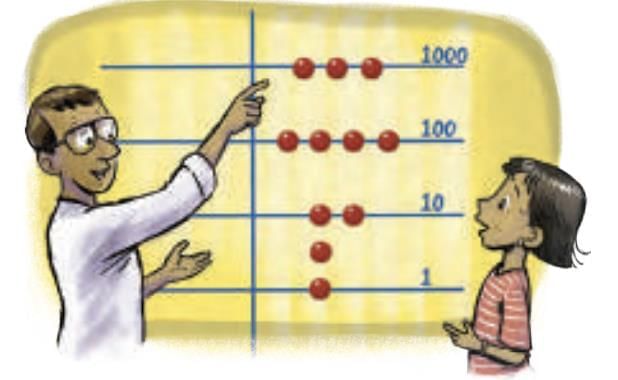  • Counters on lines representing powers of 10.

Place Value RepresentationI. Mesopotamian Number System

  • Initially used symbols for landmark numbers.
  • Developed base-60 (sexagesimal) system.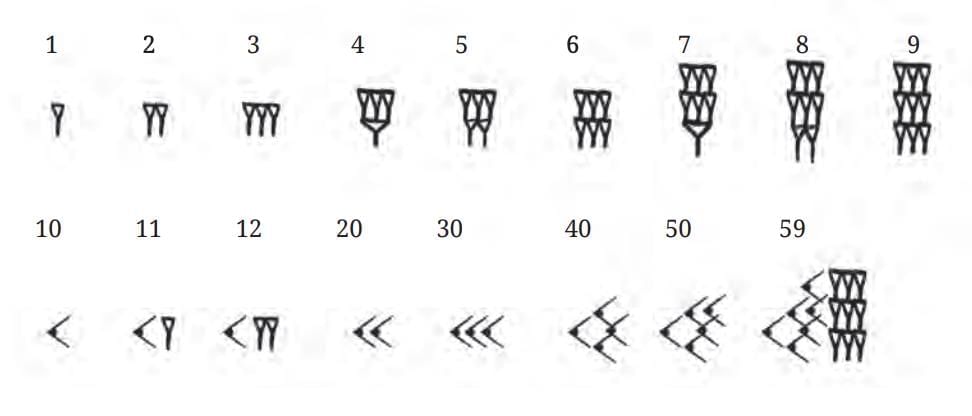
  • Symbols: 1 and 10.
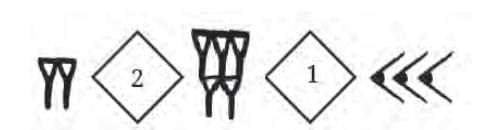  • Numbers grouped by powers of 60 (e.g., 7530 = 2×3600 + 5×60 + 30).
  • Positional system: Place of symbol determines value.
  • Placeholder symbol (like 0) introduced for blanks.
  • Influence seen in modern time measurement (60 min = 1 hour, 60 sec = 1 min).

II. Mayan Number System

  • Central America, 3rd–10th centuries CE.
  • Place value system with base-20, used placeholder for 0 (shell symbol).
  • Dots = 1, Bars = 5; numbers written vertically.

III. Chinese Number System

  1. Type of System
    • Used rod numerals.
    • Decimal system (base-10).
    • In use from 3rd century AD.
  2. Symbols
    • Separate symbols for 1–9.
    • Vertical position of the symbol indicates powers of 10.
  3. Placeholders
    • Blank spaces used as placeholders to represent missing values.
    • This is similar to the Hindu number system.

Significance

  • Early use of positional notation.
  • Enabled representation of large numbers efficiently.

IV. Hindu Number System

  1. Base-10 system
    • Also called the decimal system.
    • Uses place value to represent numbers.
  2. Symbols / Digits
    • 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
  3. Use of Zero (0)
    • Used both as a digit and as a number.
    • Introduced around 200 BCE.
    • Codified by Aryabhata and Brahmagupta.
  4. Advantages
    • Allows unambiguous representation of numbers.
    • Facilitates arithmetic operations like addition, subtraction, multiplication, and division.
  5. Significance
    • Foundation for modern mathematics including algebra, analysis, and computational methods.