Introduction
In this chapter, we will learn about measuring how far or how near things are. We will also learn about different units we use to measure length and how they are related to each other.Let Us Find
Identify the appropriate units for measuring each of the following.
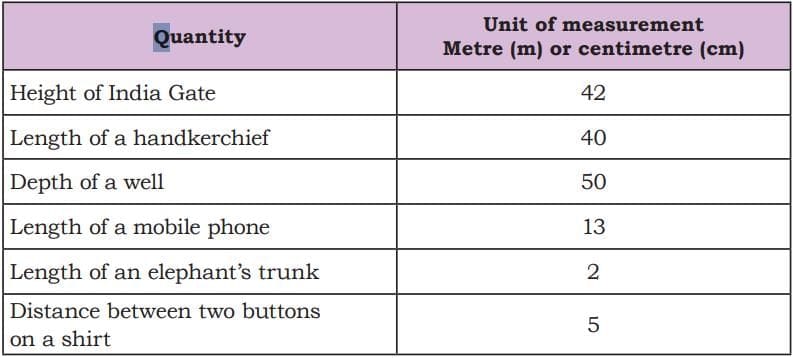
- We use different units to measure different lengths. For example, we use metre (m) or centimetre (cm).
- Height of India Gate: This is a big structure, so we use metre (m).
- Length of a handkerchief: This is small, so we use centimetre (cm). cm)
- Depth of a well: This can be deep, so we use metre (m).
- Length of a mobile phone: This is small, so we use centimetre (cm). (
- Length of an elephant’s trunk: This is quite long, so we use metre (m).
- Distance between two buttons on a shirt: This is very small, so we use centimetre (cm).
Different Units but Same Measure
- Sometimes, the same length can be written using different units. Let’s see how Shikha and Sonu are measuring saris and stoles.
- We can use a double number line to understand this better. Remember, 1 metre (m) = 100 centimetres (cm).

- Let’s match the measures:
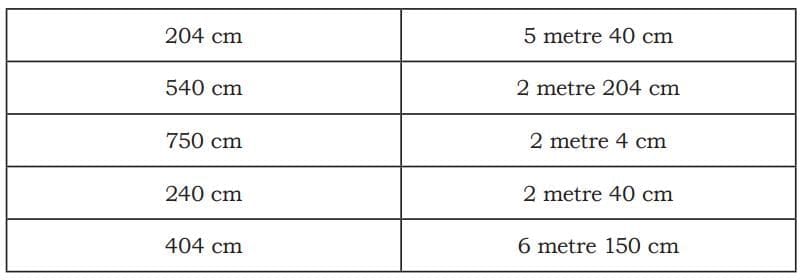
Let Us Compare
Let’s compare different lengths using the signs < (less than), > (greater than), or = (equal to).
Remember: 1 m = 100 cm
Comparing lengths of rods:
- (a) 456 cm ____ 5 m
Convert 5 m to cm: 5 m = 5 x 100 cm = 500 cm. So, 456 cm < 500 cm. - (b) 55 cm 200 cm ____ 200 cm 54 cm
Left side: 55 cm + 200 cm = 255 cm. Right side: 200 cm + 54 cm = 254 cm. So, 255 cm > 254 cm. - (c) 6 m 5 cm ___ 6 m 50 cm
Here, metres are the same (6 m). Compare the centimetres: 5 cm and 50 cm. So, 6 m 5 cm < 6 m 50 cm. - (d) 2 m 150 cm ___ 3 m 50 cm
Convert 150 cm to metres: 150 cm = 1 m 50 cm. So, 2 m 150 cm = 2 m + 1 m 50 cm = 3 m 50 cm. So, 3 m 50 cm = 3 m 50 cm. - (e) 238 cm ____ 138 cm 1 m
Convert 1 m to cm: 1 m = 100 cm. Right side: 138 cm + 100 cm = 238 cm. So, 238 cm = 238 cm. - World’s tallest statue comparison:

- Statue of Unity, India: 182 m
- Spring Temple Buddha, China: 128 m
- Statue of Guanyin of Nanshan, China: 108 m
- Statue of Liberty, USA: 93 m
- The Motherland Calls, Russia: 91 m
- Christ the Redeemer, Brazil: 38 m
Measuring Long Distances
For very long distances, we use special tools and units. We often use kilometre (km) for long distances.
Here are some ways to measure long distances:
• Long Tape: A very long measuring tape.
• Rangefinder: A device that measures distance to a target.

• Laser Distance Meter: Uses a laser to measure distance.

• Rodometer (measuring wheel): A wheel that measures distance as it rolls.

Try yourself:
What unit do we often use for long distances?
- A.Meter
- B.Centimetre
- C.Mile
- D.Kilometre
View SolutionKilometre Race
Sheena and Jennifer are organising a 3-km race. Let’s help them!
Remember: 3 km = 3 x 1000 m = 3000 m
- 1. Water stations are to be arranged after every 500 m. How many water stations must be set up? At what positions from the starting point will these water stations be placed?
- Total distance = 3000 m.
- Water stations every 500 m.
- Number of stations = 3000 m ÷ 500 m = 6 stations.
- Positions: 500 m, 1000 m, 1500 m, 2000 m, 2500 m, 3000 m (finish line).
- 2. Children need to stand at an interval of 300 mto direct the runners. How many children are needed? At what positions from the starting point will the children be standing?
- Total distance = 3000 m.
- Children every 300 m.
- Number of children = 3000 m ÷ 300 m = 10 children.
- Positions: 300 m, 600 m, 900 m, 1200 m, 1500 m, 1800 m, 2100 m, 2400 m, 2700 m, 3000 m.
- 3. Red and blue flags are to be placed alternately at every 50 m. How many red and blue flags are needed till the finish line?
- Total distance = 3000 m.
- Flags every 50 m.
- Number of flag positions = 3000 m ÷ 50 m = 60 positions.
- Since flags are placed alternately (red, blue, red, blue…), half will be red and half will be blue.
- Number of red flags = 60 ÷ 2 = 30 red flags.
- Number of blue flags = 60 ÷ 2 = 30 blue flags.
The World of Small Things
How do we measure very small things like a sprout, small screws, or a nail?

Small Things
- We use a smaller unit called millimetre (mm).
- Look at your scale. You will see small marks between 1 cm and 2 cm. If you count them, there are ten small marks.

- Each of these small parts is called 1 millimetre (mm).
- So, 1 centimetre (cm) = 10 millimetres (mm).

- These small marks help us measure very small lengths accurately.
Relationships between Different Units
Let’s summarise the relationships between different units of length:
• 10 mm = 1 cm (Millimetre to Centimetre)
• 100 cm = 1 m (Centimetre to Metre)
• 1,000 m = 1 km (Metre to Kilometre)
Try yourself:
How many millimeters are in one centimeter?
- A.15 mm
- B.20 mm
- C.10 mm
- D.5 mm
View SolutionAdding and Subtracting Lengths
We can add and subtract lengths just like we add and subtract numbers. We need to be careful with units.
Example 1: Saji’s walk
- Saji walked 3 km 450 m in the morning and 4 km 650 m in the evening. How much did he walk in total?
- Method 1: Adding km and m separately
- Add kilometres: 3 km + 4 km = 7 km.
- Add metres: 450 m + 650 m = 1100 m.
- Convert 1100 m to km and m: 1100 m = 1000 m + 100 m = 1 km100 m.
- Add the converted metres to kilometres: 7 km + 1 km 100 m = 8 km 100 m.
- Method 2: Convert everything to metres and then add
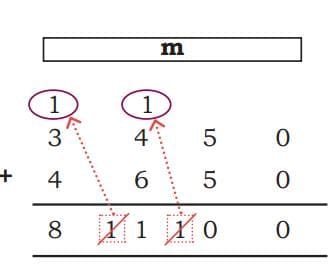
- 3 km 450 m = 3 x 1000 m + 450 m = 3000 m + 450 m = 3450 m.
- 4 km650 m = 4 x 1000 m + 650 m = 4000 m + 650 m = 4650 m.
- Total distance = 3450 m + 4650 m = 8100 m.
- Convert 8100 m to km and m: 8100 m = 8000 m + 100 m = 8 km 100 m.
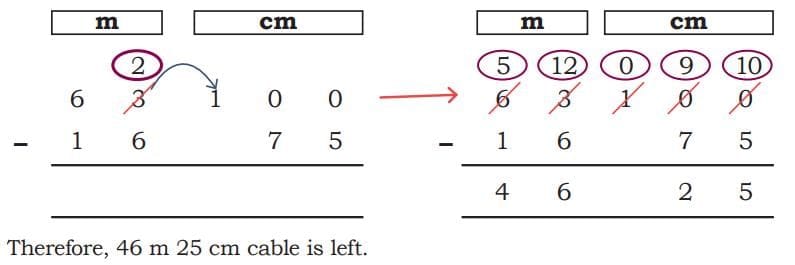
- Example 2: Cable left
- Electricians need 63 m of cable. They used 16 m 75 cm in the first room. What is the length of cable left?
- Method 1: Convert everything to cm and then subtract
- Total cable needed: 63 m = 63 x 100 cm = 6300 cm.
- Cable used: 16 m 75 cm = 16 x 100 cm + 75 cm = 1600 cm + 75 cm = 1675 cm.
- Cable left = 6300 cm – 1675 cm = 4625 cm.
- Convert 4625 cm to m and cm: 4625 cm = 4600 cm + 25 cm = 46 m 25 cm.
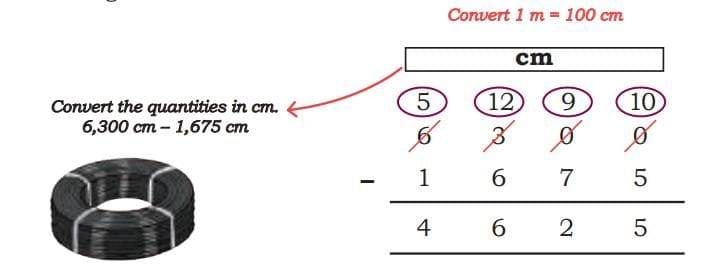
- Method 2: Subtracting m and cm separately (with borrowing)
Multiplying and Dividing Lengths
We can also multiply and divide lengths.
- Example 1: Cloth for shirts
- We need 1 m 80 cm cloth for one shirt. How much cloth is needed for 20 children?
- Method 1: Multiply m and cm separately
- Multiply metres: 20 x 1 m = 20 m.
- Multiply centimetres: 20 x 80 cm = 1600 cm.
- Convert 1600 cm to metres: 1600 cm = 16 x 100 cm = 16 m.
- Add the metres: 20 m + 16 m = 36 m.
- Method 2: Convert everything to cm and then multiply
- 1 m 80 cm = 100 cm + 80 cm = 180 cm.
- Total cloth = 20 x 180 cm = 3600 cm.
- Convert 3600 cm to metres: 3600 cm = 36 x 100 cm = 36 m.
- Example 2: Cost of cloth
- A shop sells cloth for ₹100 for 5 m. How much money is needed to buy 1 m cloth?
- Cost of 5 m cloth = ₹100.
- Cost of 1 m cloth = ₹100 ÷ 5 = ₹20.
- Example 3: Embroidery thread
- Anita needs a 1 m long thread to embroider a 50 cm sari. How much thread would she need for a 5 m sari border?
- For 50 cm sari, thread needed = 1 m.
- 5 m sari = 500 cm sari.
- Number of 50 cm sections in 500 cm = 500 cm ÷ 50 cm = 10 sections.
- Thread needed = 10 x 1 m = 10 m.
- If a 1 m long thread costs ₹50, how much money will be needed to buy 10 m thread?
- Cost of 1 m thread = ₹50.
- Cost of 10 m thread = 10 x ₹50 = ₹500.
- Example 4: Road laying work
- A road 12 km 600 m long is being laid. Workers complete the work in 6 days, laying an equal length each day. How much road-laying work is done each day?
- Total length of road = 12 km 600 m.
- Number of days = 6.
- Convert total length to metres: 12 km 600 m = 12 x 1000 m + 600 m = 12000 m + 600 m = 12600 m.
- Road laid each day = 12600 m ÷ 6 = 2100 m.
- Convert 2100 m to km and m: 2100 m = 2000 m + 100 m = 2 km 100 m.
Try yourself:
How much cloth is needed for 20 children if one shirt requires 1 m 80 cm?
- A.20 m
- B.36 m
- C.10 m
- D.30 m
View SolutionLet Us Estimate
Estimating means making a good guess about a measurement without actually measuring it. We use things we already know as a reference.
Height of a single-storeyed house: You can estimate it to be around 3-4 metres.
Height of an electric pole: You can estimate it to be around 8-10 metres.
- The height of the tallest building in your neighbourhood. What did you use as a reference to estimate the height?
- Example: If you know a 2-storey house is about 6 metres tall, you can use that to guess the height of a taller building.
- The height of the tallest tree in your neighbourhood. What did you use as a reference?
- Example: You can compare it to the height of a building or a known object.
- The depth of a well or swimming pool in your neighbourhood. How did you find out?
- Example: You can drop a stone and listen for the splash, or compare it to your own height.
Let Us Explore (Feet and Inches)
In daily life, we also use other units for measuring length, especially for height. These are feet (ft) and inches (in).
Look at your ruler. Some rulers also have inches marked on them.
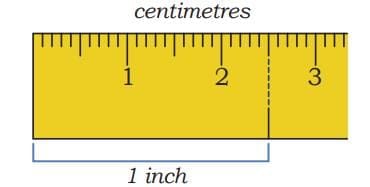
• 1 inch = approximately 2 cm 5 mm (or 2.5 cm)
• 1 foot = 12 inches
• 1 foot = approximately 30 cm