Introduction
Number system is a writing system used for expressing numbers. A number is a mathematical object used to count, label and measure.
Types of Numbers
Natural numbers: All counting numbers are called natural numbers. It is denoted by “N”.
Example: N = {1, 2, 3, 4 … .}
Natural numbers are represented on the number line as follows:

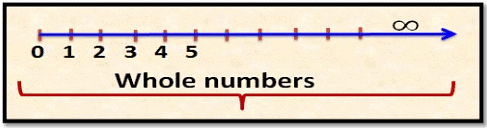
Whole numbers: The group of natural numbers including zero is called whole numbers. It is denoted by “W”. Zero is a very powerful number because if we multiply any number with zero it becomes zero. All natural numbers along with zero are called whole numbers.
Example: W = {0, 1, 2, 3, 4 … .}
Whole numbers are represented on number line as follows:
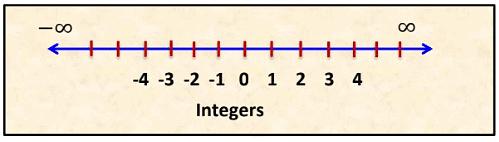
Integers: The collection of all whole numbers and negatives of all natural numbers or counting numbers are called integers. They are denoted by “Z” or “I”. All whole numbers are integers, but all integers are not whole numbers
Example: Z or I = {… − 3, −2, −1, 0, 1, 2, 3 … . .}
Integers represented on number line as follow:
Real numbers
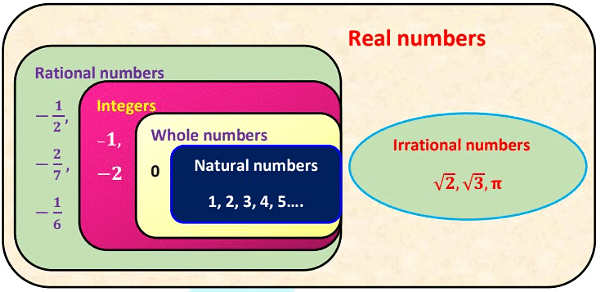
- The collection of rational & irrational numbers together forms real numbers. The set of real numbers is denoted by symbol R. How do you know whether any number is real number or not?
- If that number can be shown on number line then that number is a real number. So, any number which can be shown on the number line is real number.
Example: √2 , √3, −5, 0 , 1/5 5 etc…. All rational numbers are real numbers but all the real numbers are not rational numbers. Also, all irrational numbers are real numbers, but the reverse is not true
Rational numbers: Numbers that can be represented in the form of p/q where p & q are integers & q ≠ 0 are called rational numbers. The word rational came from the word ‘ratio’. It is denoted by letter Q and Q is taken from the word quotient. All integers are rational numbers.
Example: Q ={1/2, 3, -4, 3/2 etc ….}
Rational numbers also include natural numbers, whole numbers and integers. This can be explained using following example:
Example: –16 can also be written as -16/1 Here p = – 16 and q = 1. Therefore, the rational numbers also include the natural numbers, whole numbers and integers.
Equivalent rational numbers: The equivalent rational numbers are numbers that have same value but are represented differently.
Example: If a/b is equivalent to c/d and a/b = x then c/d = x
Also, if a/b = c/d, then a x d = b x c.
Irrational numbers: A number which can’t be expressed in the form of p/q and its decimal representation is non-terminating and non-repeating is known as irrational numbers. It is denoted by “S”.
Example: S = √2 = 1.4142135… . , √3 = 1.73205 … . , etc
Methods to determine rational number between two numbers
We know that there are infinitely many rational numbers between any given rational numbers. Hence, for determining one or more than one rational number between two given rational numbers we use the following methods
(i) When one rational number is to be determined:
Let a and b be two rational numbers, such that b > a. Then, 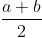 is a rational number lying between a and b
is a rational number lying between a and b
Example: Find a rational number between 4 and 5 Here, 5 > 4
We know that, if a and b are two rational numbers, such that b > a. Then, 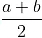 is a rational number lying between a and b.
is a rational number lying between a and b.
So, a rational number between 4 and 5 = 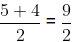
(ii) When more than one rational number are to be determined:
Let a and b be two rational numbers, such that b > a and we want to find n rational numbers between a and b. Then, n rational numbers lying between a and b are
(a + b), (a + 2d ), (a + 3d), ……….(a + nd), where, d = ( b -a ) / (n + 1)
Here, a and b are two rational numbers n is the number of rational numbers between a and b
Example (i): Find six rational numbers between 3 and 4
Here, 4 > 3
So, let a = 3 and b = 4 and n = 6
Since, d = b -a / n + 1
Now,
Hence, the required six rational numbers lying between 3 and 4 are
Example (ii): Find four rational numbers between − 6 and– 7.
Here, −6 > −7
Let a = − 7, b = − 6 and n = 4
Now, d = b -a / n + 1
=
So, four rational numbers between – 6 and − 7 are (a + d), (a + 2d), (a + 3d) and (a + 4d)
i.e.,and
=and
=and
The above rational numbers are the rational numbers which lie between – 6 and – 7.
Try yourself:Which of the following is an example of a rational number?
- A.π
- B.√2
- C. 3/4
- D.e
Irrational number
A number which can’t be expressed in the form of p/q and its decimal representation is non-terminating and non-repeating is known as irrational numbers. The set of irrational numbers is denoted by “S”.
Example: S = √2 ,√3 , π, etc. ..
Locate an irrational number on the number line:
We see how to locate an irrational number on number line with the help of following example:
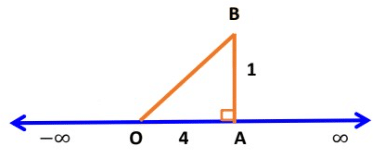
Example: Locate √17 on the number line
Here, 17 = 16 + 1 = (4)2 + (1)2 (Sum of squares of two natural numbers)
So, we take a = 4 and b = 1
Now, draw OA = 4 units on the number line and then draw AB = 1 join OB.
By using Pythagoras theorem, in ∆OAB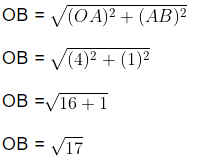
Taking O as the centre and radius equal to OB, draw an arc, which cuts the number line at C. Hence, OC represents √17.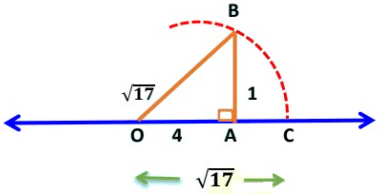
Real Numbers and their Decimal Expansion
Real numbers: The collections of rational & irrational numbers together form real numbers. They are denoted by R. Every point on the number line is a real number.
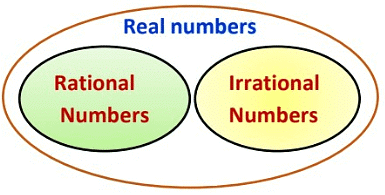
Rational and Irrational numbers are Subsets of Real Numbers
Example: √2, √3, −5, 0, 1/5, 5 etc…. All rational numbers are real number but all real numbers are not rational numbers. Also, all irrational numbers are real number, but the reverse case is not true.
Real numbers and their decimal expansion: The decimal expansion of real numbers can be either terminating or non – terminating, repeating or non – terminating non – repeating. With the help of decimal expansion of real numbers, we can check whether it is rational or irrational.
(i) Decimal expansion of rational numbers:
Rational numbers are present in the form of p/q, where q ≠ 0, on dividing p by q, two main cases occur,
(a) Either the remainder becomes zero after few steps
(b) The remainder never becomes zero and gets repeating numbers.
Case I: Remainder becomes zero
On dividing p by q, if remainder becomes zero after few steps, and then the decimal expansion terminates or ends after few steps. Such decimal expansion is called terminating decimal expansion.
Example: 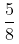
On dividing
we get exact value 0.625 and remainder is zero.
So, we say thatis a terminating decimal expansion.
On dividingwe get exact value 0.625 and remainder is zero. So, we say that
is a terminating decimal expansion.
Case II: Remainder never becomes zero
On diving p by q, if remainder never becomes zero and the sets of digits repeats periodically or in the same interval, then the decimal expansion is called non – terminating repeating decimal expansion. It is also called non – terminating recurring decimal expansion.
Example (i):
= 0.333… . . or
= 0. 3= [The block of repeated digits is denoted by bar ‘– ‘over it]
On dividingwe get the repeated number 3 and remainder never becomes zero. Hence, 1 by 3 has a non – terminating repeating decimal expansion.
Example (ii): 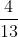
Hence,= 0.
On dividing 4 by 13 we get the repeated numbers 0.30769230 again and again, and remainder never becomes zero. Hence, 4 by 13 has a non – terminating repeating decimal expansion.
Methods to Convert Non – Terminating Repeating Decimal Expansion in the form of p by q
Suppose the number is in the form of 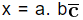 ( and we have to convert the given number in the form of p by q. Follow the following steps:
( and we have to convert the given number in the form of p by q. Follow the following steps:
Step I: Firstly, transform the non – repeated digits between decimal point and repeating number to left side of decimal by multiplying both sides by 10n
Where n = number of digits between decimal points and repeating numbers. i.e., 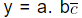 . (In the above expression we see that one digit “b” exist between decimal point and repeating number. Hence,we multiply both side by 101. We get,
. (In the above expression we see that one digit “b” exist between decimal point and repeating number. Hence,we multiply both side by 101. We get,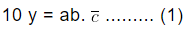 Step II: Count the number of digits in repeating number and then multiply equation (1) by that power of 10 and the equation becomes
Step II: Count the number of digits in repeating number and then multiply equation (1) by that power of 10 and the equation becomes
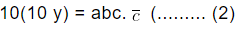 Step III: Subtract equation (1) from equation (2) we get,
Step III: Subtract equation (1) from equation (2) we get,
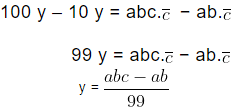 Example (i): Express in the form of p by q
Example (i): Express in the form of p by q
Assume the given decimal expansion as x
Let,
x =
x = 0.666 … … . . (i)
Here, only 1 digit is repeating. Hence, multiplying both side of equation (i) by 10 we get,
10x = 6.66… … … (ii)
Subtracting equation (i) from (ii) we get,
10x – x = 6.66 – 0.66
9x = 6.66 – 0.66
9x = 6
x = 6/9 = 2/3
Hence,
Example (ii): Express 0.4 in the form, where p and q are integers and q ≠ 0
Let, x = 0.43535 ……(i)
Here, we see that one digit exit between decimal point and recurring number
So, we multiply both sides of equation (i) by 10, we get
10x = 4.3535 …… (ii)
Here we see that two digits are repeated in the recurring number
So, we multiply equation (ii) by 100, we get
1000x = 435.3535 …… (iii)
Subtracting equation (ii) from equation (iii), we get
1000x − 10x = 435.3535 − 4.3535
990x = 431
x =
Hence,
Example (iii): Express 0.00232323…. in the form, where p and q are integers and q ≠ 0
Let, x = 0.00232323 = 0.00
……(i)
Here, we see that two digits exist between decimal point and recurring number
So, we multiply both sides of equation (i) by 100,
100x = 0.232323…… (ii)
Here we see that two digits are repeated in the recurring number
So, we multiply equation (ii) by 100, we get
10000x = 23.2323 …… (iii)
Subtracting equation (ii) from equation (iii), we get
10000x − 100x = 23.2323 − 0.232329
990x = 23
x =
Hence, 0.002323 =
| Also read: HOTS Questions: Number System |
Decimal Expansion of Irrational Numbers
The decimal expansion of an irrational numbers is non-terminating non-recurring or a number whose decimal expansion is non – terminating and non-recurring is called irrational.
Example: √3 and π are the examples of irrational numbers because, the values of √3 = 1.7320508075688772…. and π = 3.14592653589793 are non-terminating non-recurring.
Example (i): Find the irrational number between and
∴
Now,Thus,
It means that the required rational numbers will lie betweenand
. Also, we know that the irrational numbers have non-terminating non-recurring decimals. Hence, one irrational number between
and
is 0.20101001000… . .
Example (ii): Find the two irrational numbers between and
If
= 0.333 (Given)
We have,= 0.333 (Given)
Hence,= 2 ×
= 2 × 0.333 = 0.666
So, the two rational numbers betweenand
may be 0.357643… and 0.43216 (In this solution we can write infinite number of such irrational numbers)
Example (iii): Find two irrational numbers between √2 and √3 .
We know that, the value of
√2 = 1. 41421356237606 and
√3 = 1.7320508075688772
From the above value we clearly say that √2 and √3 are two irrational numbers because the decimal representations are non-terminating non-recurring. Also, √3 > √2
Hence, the two irrational numbers may be 1.501001612 and 1.602019
Try yourself: Which of the following numbers is an irrational number?
- A.0.121212…
- B.0.3333…
- C.√9
- D.√5
Operations on Real Numbers
We know that, “The collection of rational & irrational numbers together forms Real numbers”.
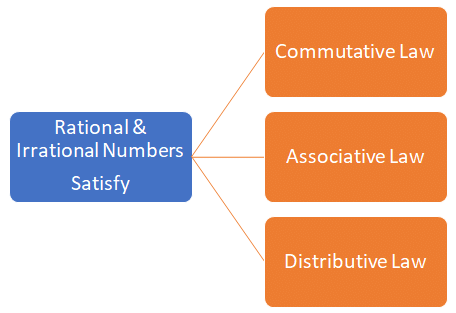
Both Rational & irrational numbers satisfy commutative law, associative law, and distributive law for addition and multiplication. However, the sum, difference, quotients and products of irrational numbers are not always irrational. If we add, subtract, multiply or divide (except by zero) two rational numbers, we still get a rational number. But this statement is not true for irrational numbers. We can see the example of this one by one
Rational Number + Rational Number = Rational Number
Let, a =
(rational) and b =
(rational),
=
=
=
=(rational number)
Rational Number – Rational Number = Rational Number
Let, a =
(rational) and b =
(rational)
=
=
=(rational number)
Rational Number X Rational Number = Rational Number
Example:
Let, a =
(rational) and b =
(rational)
Hence,×
=
(rational)
Rational Number / Rational Number = Rational Number
Let, a =  (rational) and b =
(rational) and b =  (rational)
(rational) divided by
divided by 
i.e.,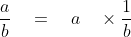
Hence,  ÷
÷  =
=  x
x  =
=  x 3
x 3 
The sum and difference of a rational number and an irrational number is an irrational number.
Example:
Let, a =  (rational) and b = √3 (irrational) then,
(rational) and b = √3 (irrational) then,
a + b =  + √3 =
+ √3 =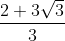 (irrational)
(irrational)
a − b =  − √3 =
− √3 =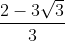 (irrational)
(irrational)
The multiplication or division of a non-zero rational number with an irrational number is an irrational number.
Example:
Let, a = (rational) and b = √2 (irrational) then,
(rational) and b = √2 (irrational) then,
ab =  × √2 =
× √2 =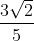 (irrational)
(irrational)
 =
= 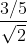 =
= 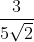 ×
× 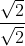 =
=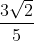 (irrational)
(irrational)
If we add, subtract, multiply or divide two irrational numbers, we may get an irrational number or rational number.
Example:
Let two irrational numbers be
a = 3 + √2 and b = 3 − √2 then
a + b = ( 3 + √2 ) + ( 3 − √2 )
= 3 + √2 + 3 − √2
= 3 + 3
= 6 (rational)
Let two irrational numbers be
a = √3 + 1 and b = √3 − 1 then
A + b = (√3 + 1 ) + (√3 − 1)
= √3 + 1 + √3 − 1
= 2√3 (irrational)
Examples: Write which of the following numbers are rational or irrational.
(a) π − 2
(b) (3 + √27 ) − (√12 + √3)
(c) 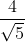
(a) π − 2
We know that the value of the π = 3.1415
Hence, 3.1415 – 2 = 1.1415
This number is non-terminating non-recurring decimals.
(b) (3 + √27 ) − (√12 + √3)
On simplification, we get
( 3+) – (
+
)
= 3 + 3√3 − 2√3 − √3
= 3 + √3 − √3
= 3, which is a rational number.
(c) 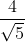
Here, 4 is a rational number and √5 is an irrational number. Now, we know that division of rational number and irrational number is always an irrational number.
Example: Add: 3 √2 + 6 √3 and √2 – 3√3
= (3 √2 + 6 √3 ) + (√2 – 3 √3 )
= (3 √2 + √2 ) + (6 √3 – 3 √3 )
= (3 + 1) √2 + (6 − 3) √3
= 4√2 + 3√3
Example: Multiply: 5√3 x 3√3
5√3 x 3√3
= 5 x 3 x √3 x √3
= 15 x 3 = 45
Try yourself:What is the value of the product of two irrational numbers?
- A. Always irrational
- B.Always rational
- C.Can be rational or irrational
- D. None of the above
Representation of √x for any positive integer x on the number line geometrically
We understand this method with the help of following steps. This construction shows that √x exists for all real numbers x > 0
Step I: Firstly mark the distance x from fixed point on the number line i.e. PQ = x
Step II: Mark a point R at a distance 1 cm from point Q and take the mid-point of PR.
Step III: Draw a semicircle, taking O as centre and OP as a radius.
Step IV: Draw a perpendicular line from Q to cut the semi-circle to find √x
Step V: Take the line QR as a number line with Q as zero.
Step VI: Draw an arc having centre Q and radius QS to represent √x on number line.
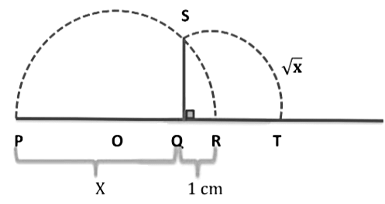
We can see this method with the help of example
Example: let us find it for x = 4.5, i.e., we find √4.5
(i) Firstly, draw a line segment AB = 4.5 units and then extend it to C such that BC = 1 unit.
(ii) Let O be the Centre of AC. Now draw the semi- circle with centre O and radius OA.
(iii) Let us draw BD from point B, perpendicular to AC which intersects semi-circle at point D.Hence, the distance BD represents √4.5 ≈ 2.121 geometrically. Now take BC as a number line, draw an arc with centre B and radius BD from point BD, meeting AC produced at E. So, point E represents √4.5 on the number line.
Radical Sign: Let a > 0 be a real number and n be a positive integer, such that
(a)  =
= 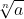 is a real number, then n is called exponent, and a is called radical and “√ ” is called radical sign.
is a real number, then n is called exponent, and a is called radical and “√ ” is called radical sign.
The expression 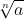 is called surd.
is called surd.
Example: If n = 2 then (4)
=
is called square root of 2.
Identities
Now we will list some identities which are related to square roots. You are familiar with these identities, which hold good for positive real number a and b. Let a and b be positive real numbers. Then,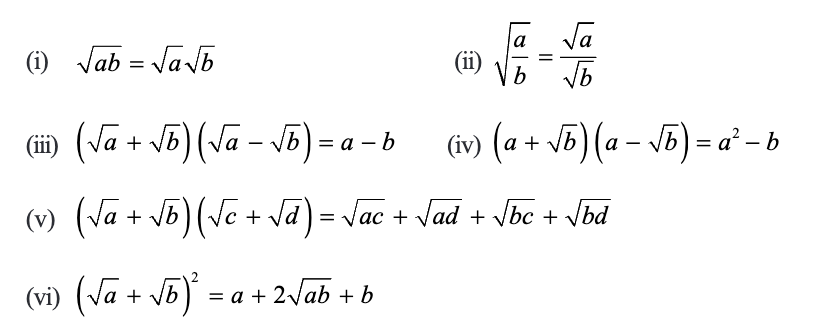
Let’s solve some examples on the basis some of identities:
Examples: Simplify each of the following
(a) x
(b)
(c) ( √2 + √3 ) (√2 – √3)
(d) (5 + √5 ) (5 – √5 )
(a) x
We know that,
x
=
=
==
2
= (25)
= 21
= 2
b)
We know that,
=
=
=(34)
= 3
(c) (√2 + √3 ) (√2 – √3)
(d) (5 + √5 ) (5 – √5 )
We know that,
Rationalising the Denominators
Looking at the value 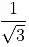 can you tell where this value will lie on the number line? It is a little bit difficult. Because the value containing square roots in their denominators and division is not easy as addition, subtraction, multiplication and division are convenient if their denominators are free from square roots. To make the denominators free from square roots i.e. they are whole numbers, we multiply the numerator and denominators by an irrational number. Such a number is called a rationalizing factor.
can you tell where this value will lie on the number line? It is a little bit difficult. Because the value containing square roots in their denominators and division is not easy as addition, subtraction, multiplication and division are convenient if their denominators are free from square roots. To make the denominators free from square roots i.e. they are whole numbers, we multiply the numerator and denominators by an irrational number. Such a number is called a rationalizing factor.
Note: Conjugate of 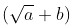 is ,
is , 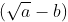 and conjugate of ,
and conjugate of , 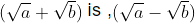
Let’s solve some examples on rationalizing the denominators:
Examples: Rationalise the denominator of the following
(a) 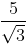
(b) 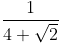
(c) 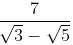
(d) 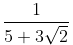
(a) 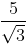
Rationalization factor for
Here, we need to rationalise the denominator i.e., remove root from the denominator. Hence, multiplying and dividing by
∴
(b) 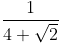
We know that the conjugate of 4 + √2 = 4 – √2
∴
(c) 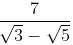
We know that the conjugate of √3 – √5 = √3 + √5
∴
(d) 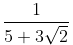
We know that the conjugate of 5 + 3√2 = 5 – 3√2
Laws of Exponent for Real Numbers
Now we will list some laws of exponents, out of these some you have learnt in your earlier classes. Let a (> 0) be a real number and m, n be rational numbers.
(i) am X an = am+n
(ii) (am)n = amn
(iii) = am-n
(iv) am X bm = (ab)m
(v) a-m = 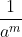
(vi) ( ) -m = (
) -m = ( )m
)m
Note: The value of zero exponent i.e. a° =1
Let us now discuss the application of these laws in simplifying expression involving rational exponents of real numbers.
Examples: Simplify each of the following
(i) (2)5 x (2)3
(ii) (43)2
(iii) 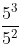
(iv) 72 × 62
(v) 6-2
(vi) 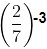
(vii) 33/2
(i) (2)5 x (2)3
We know that,
am x an = am+n
Hence,
(2)5 × (2)3 = (2)5+3 = (2)8
(ii) (43)2
We know that,
(am)n = amn
(43)2 = (4)3 ×2 = (4)6
(iii) 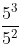
We know that,
am/an = am-n
== 53-2 = 51
(iv) 72 × 62
We know that,
am x bm = (ab)m
(7)2 × (6)2 = (7 × 6)2 = (42)2
(v) 6-2
We know that,
a-m =1/am
6-2 = 1/62 = 1/36
(vi) 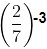
We know that
(vii) 33/2
We know that
Try yourself:Which of the following best describes a number with a decimal representation like 0.3333…?
- A.Finite decimal
- B.Non-terminating non-repeating decimal
- C. Terminating decimal
- D.Non-terminating repeating decimal
Summary
1. Rational Numbers:
- A number is classified as rational if it can be expressed as a fraction p/q where p and q are integers and q ≠ 0.
- The decimal expansion of a rational number is either terminating or non-terminating but recurring.
2. Irrational Numbers:
- A number is classified as irrational if it cannot be expressed as p/q, where both p and q are integers and q ≠ 0.
- The decimal expansion of an irrational number is non-terminating and non-recurring.
3. Real Numbers:
- The set of all rational and irrational numbers combined forms the collection of real numbers.
4. Operations with Rational and Irrational Numbers:
- If r is rational and s is irrational, then:
- r + s and r – s are irrational.
- r × s and r / s (given r≠ 0) are irrational.
5. Identities for Positive Real Numbers:
For any positive real numbers a and b:
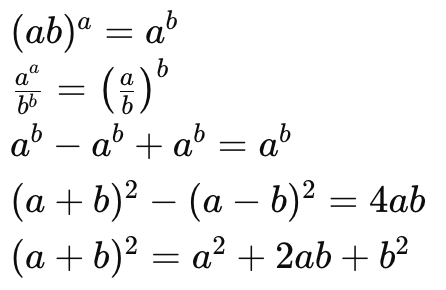
6. Rationalizing the Denominator:
To rationalize the denominator in terms like 1 / a + b multiply by the conjugate a – b / a – b.
7. Exponential Properties:
Let a > 0 be a real number and p and q be rational numbers. Then:
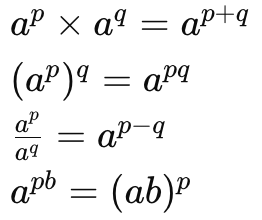
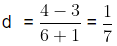
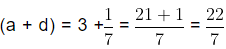
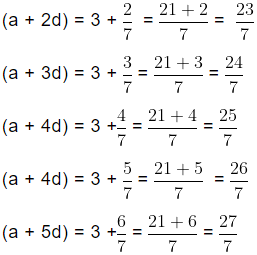
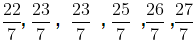
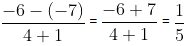
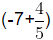
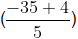
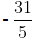

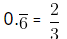

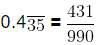
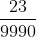
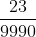
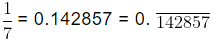
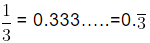
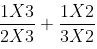
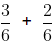
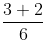
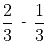
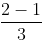
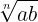
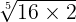
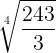
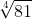
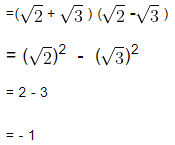
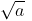
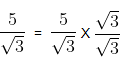
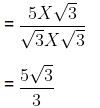
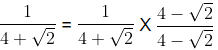
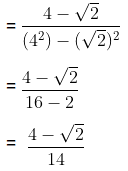
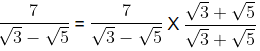
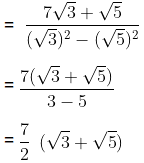
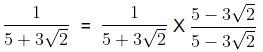
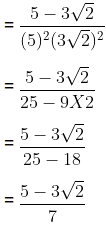
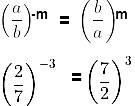
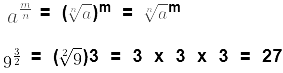


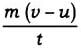
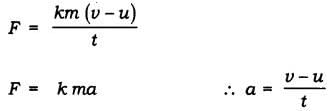

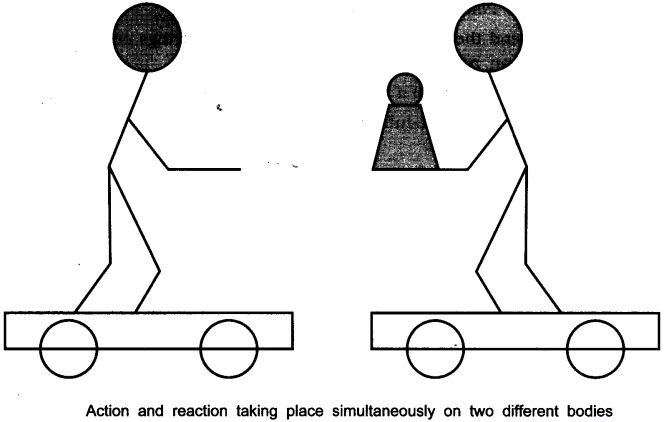
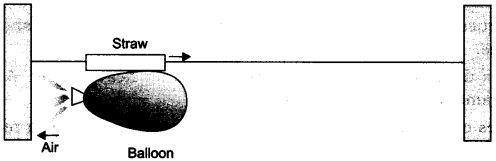 Observation:
Observation: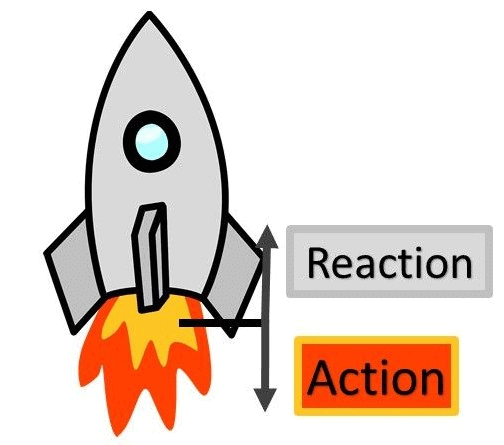




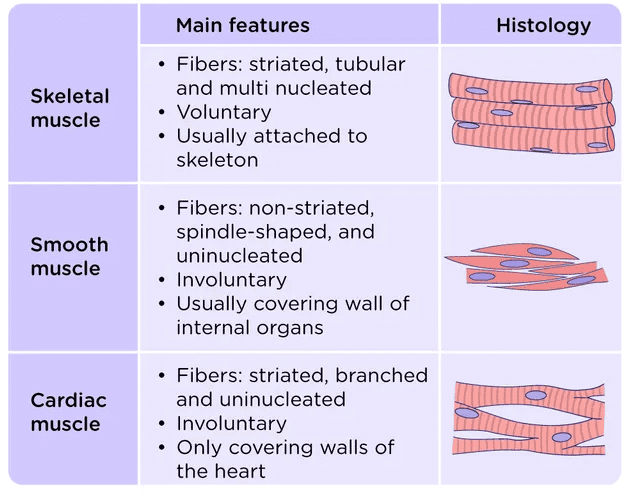
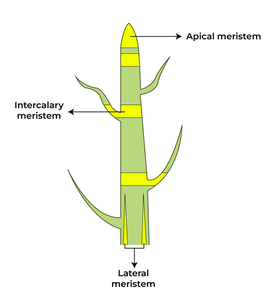 Meristematic Tissue
Meristematic Tissue (c) The tips of root stopped growing in jar 2 because the tips of these roots were cut down and the tissues which helps in the growth of roots i.e., meristematic tissues are removed from it.
(c) The tips of root stopped growing in jar 2 because the tips of these roots were cut down and the tissues which helps in the growth of roots i.e., meristematic tissues are removed from it.