Page No. 136
Alphabet Cutout
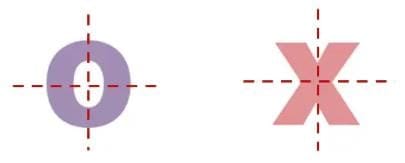
Q1: Which of the following alphabet cutouts can be made by just drawing half (1/2) or quarter (1/4) of the letter? You can do it by drawing lines of symmetry on the letters.

Which of the letters have a horizontal line of symmetry? _________________
Which of the letters have a vertical line of symmetry? ____________________
Which letters have both vertical and horizontal lines of symmetry?________
Ans: (i) Alphabets made by drawing 1/2 of the letter: E, T, and V.
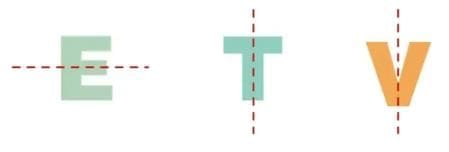
Explanation: a letter that has a single line of symmetry can be made by drawing one half and reflecting it. For example, E here is shown with a horizontal line of symmetry, while T and V have vertical lines of symmetry.
(ii) Alphabets made by drawing 1/4 of the letter: O and X.
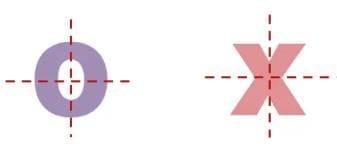
(iii) Letters with horizontal line of symmetry:
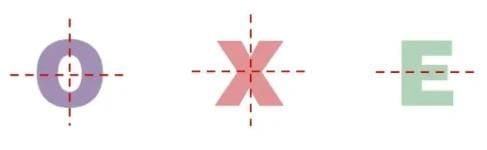
Explanation: For (ii), letters like O and X have both vertical and horizontal lines of symmetry, so one quarter of these letters is enough to make the whole letter by repeating the quarter piece.
(iv) Letters with vertical line of symmetry:
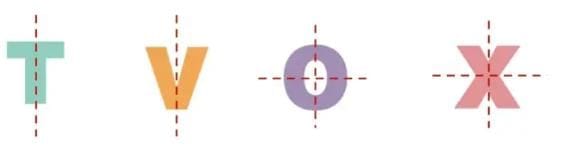
(v) Letters with both vertical and horizontal lines of symmetry:
Let Us Do
Q1: Use lines of symmetry to make paper cutouts of diya, boat, and other designs. Look along the border of the page to find the pictures.
Ans: Do it yourself. Hint: Fold the paper along the line of symmetry and cut out the shape on one side only. When you unfold the paper you will get a complete symmetrical design.
Page No. 137-138
Let Us Make a Windmill Firki
Q1: Observe the dot in the firki. Does the firki look the same after 1/4,1/2,3/4 and a full turn?
Ans: Yes, the firki looks the same after 1/4, 1/2, 3/4, and a full turn.
Explanation: The firki has four identical blades placed around the centre. Because the blades are identical, turning the firki by 1/4 turn (90°) moves one blade to the place of the next; the pattern lines up exactly after 1/4, 1/2, 3/4 and full turns.
Q2: Observe the letters below. Do they look the same when turned? Dots have been marked on the letters to keep track of the orientation of letters. You may also cut out the letters and fix the centre point of the letter by a nail or use tracing paper to check if the letter looks the same when turned.
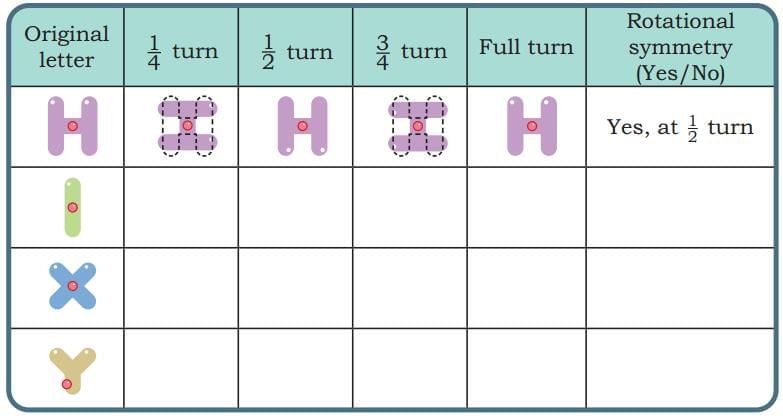
Ans:
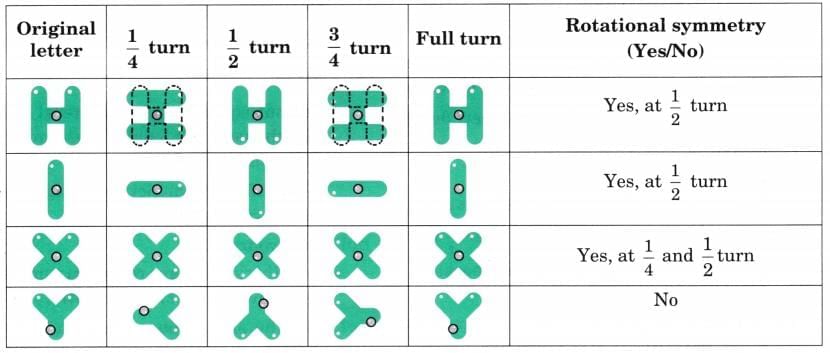
Explanation: For the letters, fix the centre point and rotate to check which letters match their original position; the pictures above show the results.
Let Us Do
Q1: Find symmetry in the digits.

Which digit(s) have reflection symmetry? ___________________________
Which digit(s) have rotational symmetry? ___________________________
Which digit(s) have both rotational and reflection symmetries? ________
Now, let us look at the following numbers: || , |00| Do these have (a) rotational symmetry, (b) reflection symmetry or (c) both symmetries? Give examples of 2-, 3-, and 4-digit numbers which have rotational symmetry, reflection symmetry, or both.Ans: (i) Digits with reflection symmetry = 1, 8, 0.
(ii) Digits with rotational symmetry = 1, 8, 0.
(iii) Digits with both rotational and reflection symmetry = 1, 8 and 0.
Q5: Now, let us look at the following numbers: ||, |00|
Do these have
(a) rotational symmetry,
(b) reflection symmetry or
(c) both symmetries?
Ans:
||, |00| have both rotational and reflection symmetry.
Q6: Give examples of 2-, 3-, and 4-digit numbers which have rotational symmetry, reflection symmetry, or both.
Ans:
(i) Numbers with Reflection Symmetry:
• 2-digit: 11, 88
• 3-digit: 181, 303, 808
• 4-digit: 1001, 1331, 8008
(ii) Numbers with Rotational Symmetry:
• 2-digit: 80, 88, 00
• 3-digit: 808, 880, 800
• 4-digit: 8008, 8888, 0880
(iii) Numbers with Both Reflection & Rotational Symmetry:
• 2-digit: 88, 00
• 3-digit: 808, 888
• 4-digit: 8008, 8888, 0880
Explanation: Reflection symmetry (also called mirror symmetry) means a vertical or horizontal line can divide the digit so that one side is the mirror image of the other. Rotational symmetry means the digit looks the same after turning by 180° (half turn) or some other fraction. The examples above are numbers that remain the same when reflected or rotated using common digit shapes; you can check each example by folding a printed number along the line of symmetry or by rotating a cutout.
Page No. 139-140
Making Designs
Q1: (a) Does the design have rotational symmetry?
Yes/No.
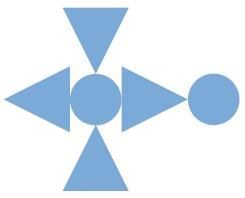
Ans: No, the design doesn’t have rotational symmetry.
Explanation: When the figure is turned it does not match its original position at fixed turns, so it is not rotationally symmetric.
(b) Try to change the design by adding some shape(s) so that the new design looks the same after a 1/2 turn. Draw the new design 2 in your notebook.
Ans:
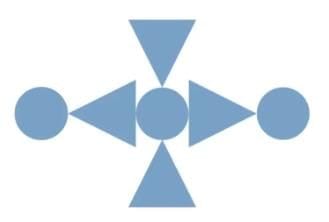
Explanation: Add symmetrical elements opposite each other so that after a half turn (180°) each part moves to the position of an identical part.
(c) Now try to modify or add more shapes so that the new design looks the same after turn.
Draw the new design in your notebook.
Ans:

Explanation: To get higher order rotational symmetry, repeat the same motif around the centre at equal angles so the design matches after the desired turn.
(d) Do the new designs have reflection symmetry? If yes, draw the lines of symmetry.
Ans: Yes, the new designs have reflection symmetry.
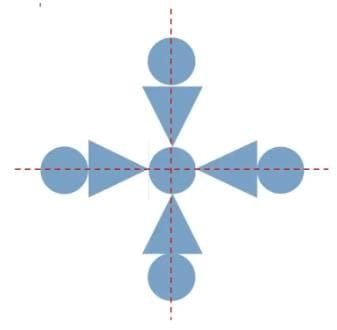
Explanation: The added shapes are placed so that a vertical or horizontal line divides the design into two mirror-image halves; the picture above shows the lines of symmetry.
Let Us Think

Q1: Does this design look the same after 1/2 turn?
Ans: Yes, the design looks the same after 1/2 turn.
Explanation: The design has two identical halves opposite each other; a half turn interchanges these halves so the design matches its original position.
Q2: Does this design look the same after a 1/4 turn?
Ans: No, the design does not look the same after a 1/4 turn.
Explanation: The design does not repeat every 90°, so a quarter turn changes the positions of parts and they do not match the original.
Colour the square given in the adjoining figure using two colours so that the design looks the same after every 1/4 turn.
How many times does this shape look the same during a full turn?
Q3: Do these designs have reflection symmetry also? Draw the line(s) of symmetry.
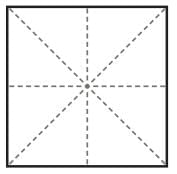
Ans:

The image looks the same after every 1/4 turn.
During a full turn, it looks the same four times. The shaded design does not have reflection symmetry.
Explanation: A design that repeats every 1/4 turn will match its original position four times during a full 360° rotation. If no mirror line divides the shaded design into identical halves, it does not have reflection symmetry.
Let Us Do
Q1: Cut out squares and equilateral triangles with the same side length. These are provided at the end of the book.
Make different symmetrical designs by using these two shapes.

Ans: (Sample)
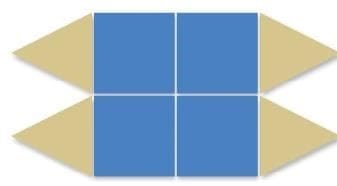
Hint: Arrange the shapes around a centre to make rotational patterns, or place them as mirror images to make reflection-symmetric designs.
Q2: Does this shape have reflection symmetry? If yes, draw its line(s) of symmetry.
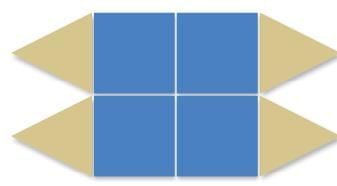
Ans: Yes, the shape has reflection symmetry. Its lines of symmetry are drawn as shown in the picture below.
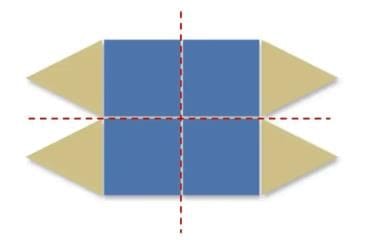
Explanation: A line drawn through the centre divides the shape into two mirror-image halves; the picture shows one or more such lines.
Q3: Does it have rotational symmetry? If yes, at which turn?
Ans: The shape has rotational symmetry of 1/2 turn also. Explanation: A half turn (180°) maps the shape onto itself because two opposite parts swap places and coincide.
Q4: Does it have both symmetries?
Ans: Yes, it has both reflection and rotational symmetry.
Let Us Explore
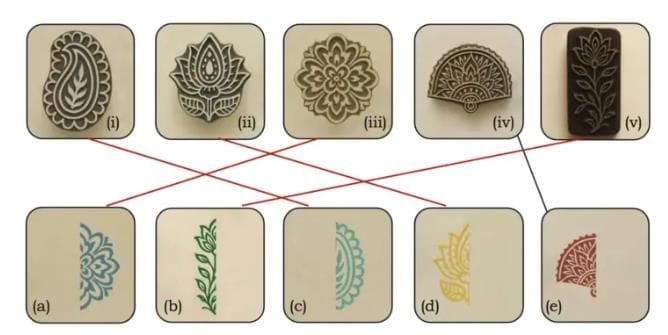
Q1: Below are images of wooden blocks and a part of their prints. Match each block to its correct print by drawing a line. One is done for you.

Ans:
Page No. 141
Q. Observe the pattern made by the wooden block below. We get the final print by using the block 4 times.
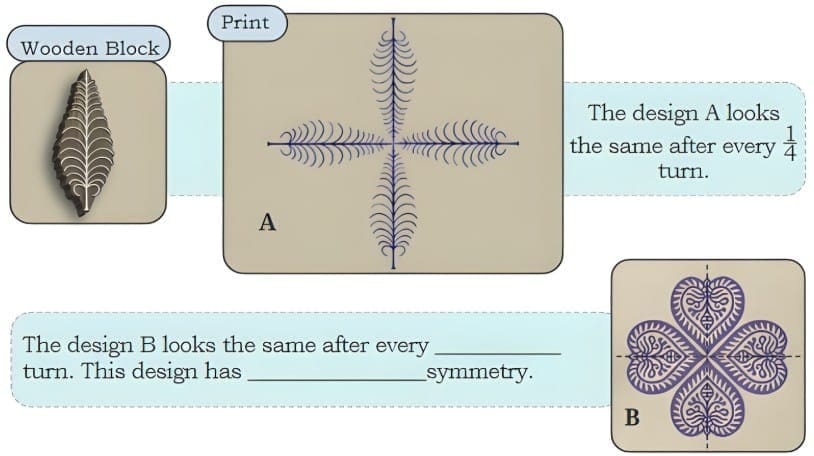
Ans:
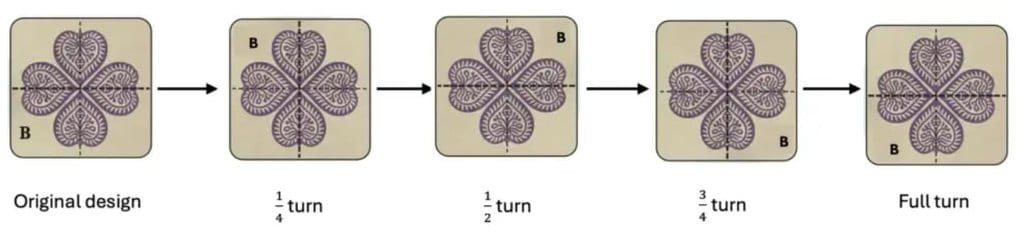
Design B looks the same after every 1/4 turn.
The design has rotational symmetry.
Explanation: The block is repeated four times around a centre so the print repeats every 90° turn.
Let us Do
Observe the shapes given on the border. Which of the shapes have reflection symmetry? Put a (✔) mark on them. Put a * on the shapes that have rotational symmetry.
Ans:
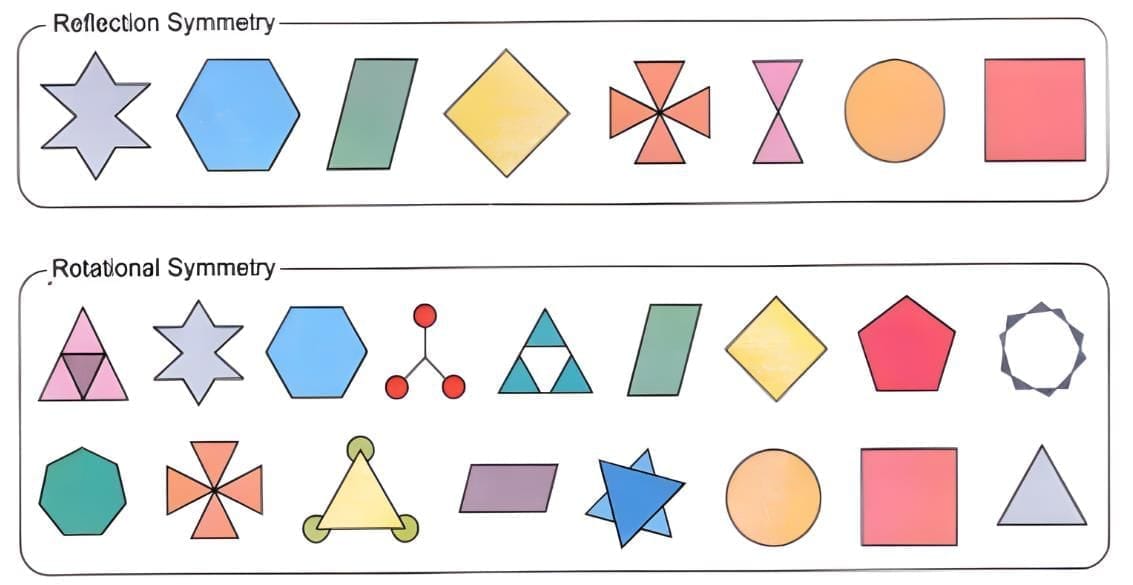
Explanation: Mark shapes that can be folded along a line to give matching halves with ✔. Put * on shapes that match themselves after a rotation by the specified angle.
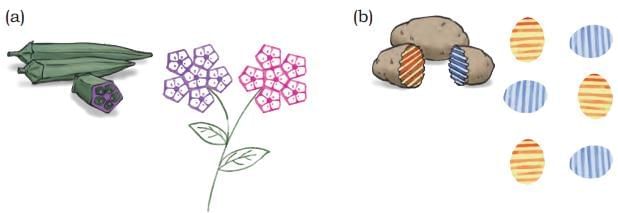
Project Work
Q1: Create symmetrical patterns and designs using vegetable blocks. Some are shown below.
Ans: Do it yourself. Suggestion: Cut vegetables into simple shapes, stamp them with ink or paint, and arrange the prints around a centre or along a mirror line to make symmetrical designs. Photograph or paste your patterns into your project notebook