Page No. 142
Let Us Do
Q1: Find the perimeter of the following shapes. All sides of the following shapes are equal.

Ans: Perimeter of a shape
= Sum of lengths of all sides
= (4 + 4 + 4 + 4 + 4) cm
= 20 cm
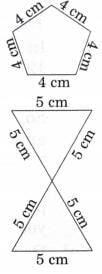
Perimeter = sum of all six equal sides.
Each side = 5 cm, number of sides = 6.
Perimeter = 5 + 5 + 5 + 5 + 5 + 5 cm
= 30 cm
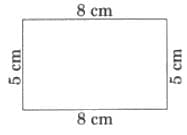
Q2: Draw two rectangles each having the following perimeters.
(a) 26 cm
Ans:
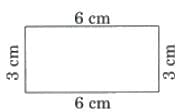
(b) 18 cm
Ans:
Page No. 143
Preetha and Adrit’s grandmother is making a rug with square patches. The picture below shows the rug.
How many patches have they used to make this?

Ans:
They have used 90 square patches to make the rug.
This number can be found by counting the number of patches in one row and multiplying by the number of rows, or by counting all patches directly.
Q: Preetha and Adrit are trying to cover their table with different shapes. Preetha covered it with triangles and circles. Adrit covered it with squares and rectangles.

They found that __________, __________ and __________ shapes cover the top of the table without gaps and overlaps. __________ shape leaves gaps.
__________ triangles cover Table 1.
__________ squares cover Table 3.
__________ rectangles cover Table 4
Ans:
They found that triangle, square and rectangle shapes cover the top of the table without gaps and overlaps. Circle shape leaves gaps.
20 triangles cover Table 1.
8 squares cover Table 3.
12 rectangles cover Table 4.
Q: To find the area of a region, we usually fill it with shapes that tile (no gaps or overlaps), like squares, rectangles and triangles.
Do circles tile? Can we use them to cover a region?
The area of Table 1 is __________ triangle units.
The area of Table 3 is __________ square units.
The area of Table 4 is __________ rectangle units
Ans:
No, circles do not tile. We cannot use them to cover a region because circles leave gaps between them when placed side by side.
The area of Table 1 is 20 triangle units.
The area of Table 3 is 8 square units.
The area of Table 4 is 12 rectangle units.
Q: Now, try to cover the top of your table without gaps and overlaps with the following objects of same size.
(a) Notebooks
(b) Lunch boxes
(c) Pencil boxes
(d) Maths textbooks
Which of the above objects covered the region completely?
Ans:
Do it yourself.
Page No. 144
Let Us Do
Preetha is playing with tiles. She covers her desk with different shapes as shown below.
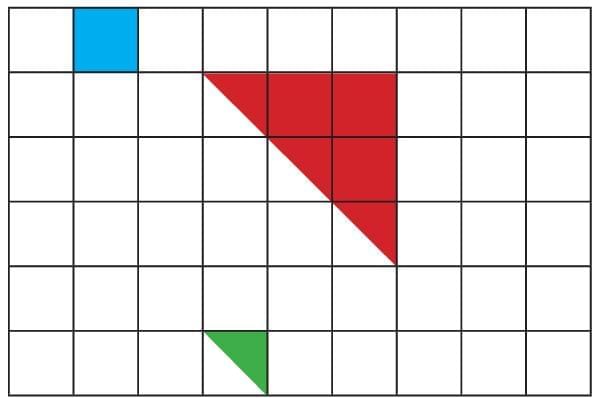
Look at the different tiles on her desk and answer how many of the following shapes will cover the desk.
(a) Green triangles _______
(b) Red triangles _______
(c) Blue squares _______
Ans:
In the given picture, the desk is made up of 54 unit squares.
(a) Two green triangles make one full square. Therefore,
Total number of green triangles = 54 × 2 = 108 green triangles.
(b) If one red triangle equals 9/2 unit squares (that is 4.5 square units), then
Total area to cover = 54 unit squares.
Number of red triangles required = 54 ÷ 4.5 = 12 red triangles.
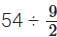
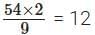
Therefore, 12 red triangles will cover the desk.
(c) One blue square = 1 unit square.
Therefore, the number of blue squares required = 54 blue squares.
Page No. 145-148
Let Us Do
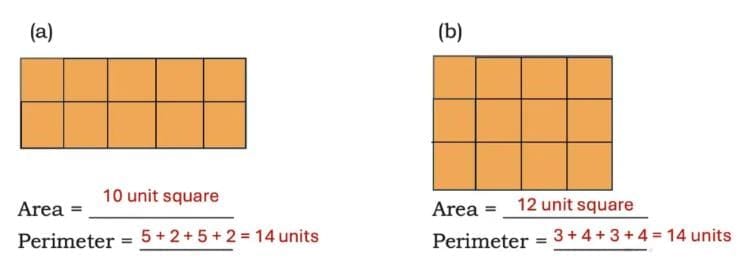
Q1: Compare the areas of the two gardens given below on the square grid. Share your observations.
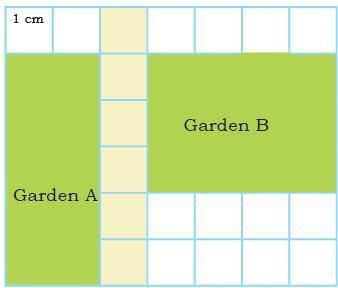
Area of Garden A = _____ cm square
Area of Garden B = _____ cm square
Ans:
Garden A is covered by 10 unit squares, each of side 1 cm.
Therefore, the area of Garden A = 10 square cm.
Garden B is covered by 12 unit squares, each of side 1 cm.
Therefore, the area of Garden B = 12 square cm.
Observation: Garden B has a larger area than Garden A by 2 square cm.
Q2: Trace your palm on the square grid given below and find the approximate area of your palm. Compare the area of your palm with your friend’s palm. Who has a bigger palm?

Ans:
Do it yourself.
Q3: Collect leaves of different kinds. Put them on a square grid and find their area.
(a) Name the leaf with the largest area.
(b) Name the leaf with the smallest area.
Ans:
Do it yourself.
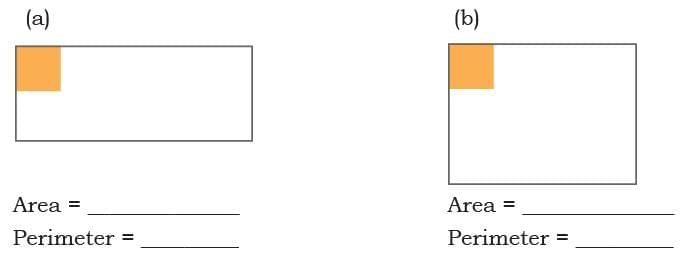
Q4: The following mats are made of square patches of equal size. How many square patches will be required to cover each mat? Would both mats require an equal or different number of patches? Trace and cut out a small square of the size given below and find the area.
Ans:
The number of square patches required to cover the mat (a) = 10 square patches.
The number of square patches required to cover the mat (b) = 12 square patches.
Therefore, both mats require a different number of patches.
Q: Trisha makes these two rectangles. She says, “I increased the area of my rectangle, and the perimeter increased. Do you think this is always true?

Ans:
Take a rectangle with length = 12 cm and breadth = 2 cm.
Area = 12 × 2 = 24 square cm.
Perimeter = 2(12 + 2) = 2 × 14 = 28 cm.
Now change the rectangle to length = 7 cm and breadth = 4 cm.
Area = 7 × 4 = 28 square cm.
Perimeter = 2(7 + 4) = 2 × 11 = 22 cm.
Here, area increased from 24 square cm to 28 square cm, but the perimeter decreased from 28 cm to 22 cm.
Therefore, Trisha’s claim is not always true. Increasing the area does not always increase the perimeter; both measures depend on the shape’s dimensions.
Let Us Explore
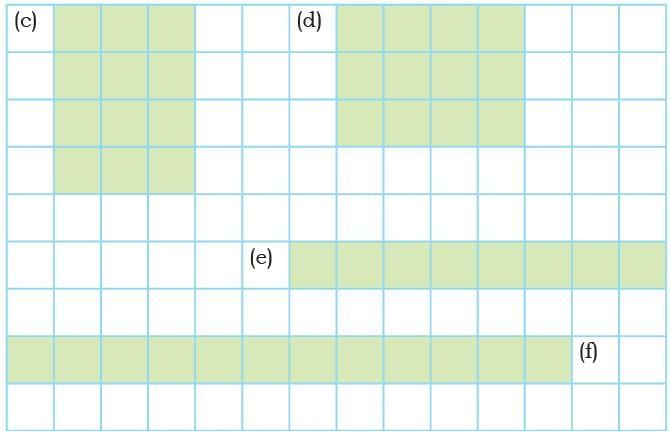
Q1: Tick the shapes with the same area. Find the perimeters of these shapes. What do you notice? Discuss.

Ans:
(a) Area = 12 square cm.
Perimeter = 6 cm + 2 cm + 6 cm + 2 cm = 16 cm.
(b) Area = 12 square cm.
Perimeter = 2 cm + 1 cm + 1 cm + 5 cm + 2 cm + 5 cm + 1 cm + 1 cm = 18 cm.
(c) Area = 12 square cm.
Perimeter = 3 cm + 4 cm + 3 cm + 4 cm = 14 cm.
(d) Area = 12 square cm.
Perimeter = 4 cm + 3 cm + 4 cm + 3 cm = 14 cm.
(e) Area = 8 square cm.
Perimeter = 8 cm + 1 cm + 8 cm + 1 cm = 18 cm.
(f) Area = 12 square cm.
Perimeter = 12 cm + 1 cm + 12 cm + 1 cm = 26 cm.
Therefore, shapes (a), (b), (c), (d) and (f) each have area 12 square cm, while (e) has area 8 square cm.
We notice that shapes with the same area can have different perimeters.
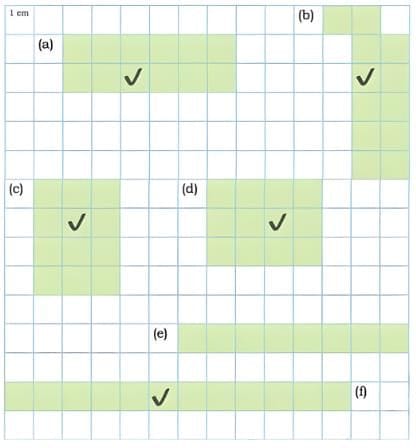
Q2: Tick the shapes with the same perimeter. Find the areas of these shapes. What do you notice? Discuss.
Ans: (a) Perimeter = 3 cm + 3 cm + 1 cm + 1 cm + 2 cm + 2 cm = 12 cm.
Area = 7 square cm.
(b) Perimeter = 3 cm + 1 cm + 1 cm + 2 cm + 2 cm + 3 cm = 12 cm.
Area = 7 square cm.
(c) Perimeter = 1 cm + 2 cm + 2 cm + 1 cm + 1 cm + 1 cm + 1 cm + 1 cm + 1 cm + 1 cm + 1 cm + 1 cm + 1 cm + 1 cm = 16 cm.
Area = 7 square cm.
(d) Perimeter = 1 cm + 4 cm + 2 cm + 1 cm + 3 cm + 5 cm = 16 cm.
Area = 7 square cm.
(e) Perimeter = 7 cm + 1 cm + 7 cm + 1 cm = 16 cm.
Area = 7 square cm.
Thus, these shapes show that different shapes can have the same area even if their perimeters are different. All these shapes have area 7 square cm.
Page No. 149-150
Let Us Do
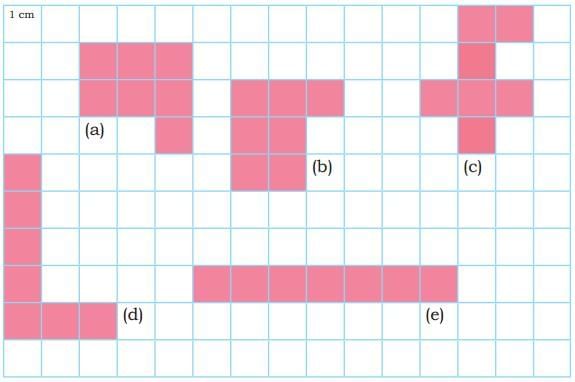
Q1: Draw different shapes having the same area as the given shape. Write the perimeter of each shape. What do you notice? Discuss.

Ans:
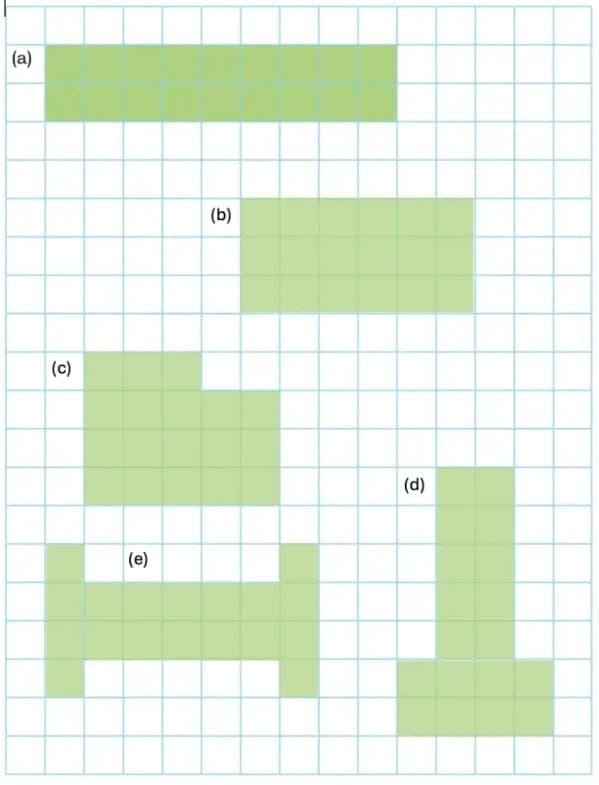
(a) Area = 18 square cm.
Perimeter = 9 cm + 2 cm + 9 cm + 2 cm = 22 cm.
(b) Area = 18 square cm.
Perimeter = 6 cm + 3 cm + 6 cm + 3 cm = 18 cm.
(c) Area = 18 square cm.
Perimeter = 3 cm + 1 cm + 2 cm + 3 cm + 5 cm + 4 cm = 18 cm.
(d) Area = 18 square cm.
Perimeter = 2 cm + 5 cm + 1 cm + 2 cm + 4 cm + 2 cm + 1 cm + 5 cm = 22 cm.
(e) Area = 18 square cm.
Perimeter = 1 cm + 1 cm + 5 cm + 1 cm + 1 cm + 4 cm + 1 cm + 1 cm + 5 cm + 1 cm + 1 cm + 4 cm = 26 cm.
Thus, shapes having the same area can have different perimeters.
Q2: Is the area of shape (a) less than the area of shape (b) given below? Discuss.
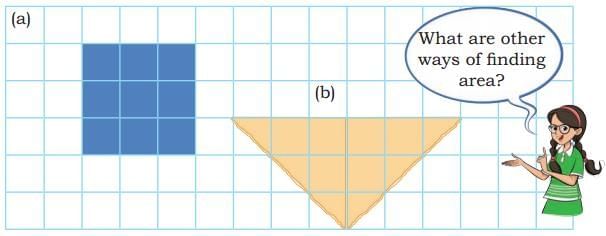
Preetha and Adrit’s grandmother is making another square patchwork. She arranges the patches as shown below. Can you guess how many patches she will need? How did you find it?
Ans:
Area of shape (a) = 9 unit squares.
Area of shape (b) = 6 full unit squares + 6 half unit squares = 6 + (6 × 1/2) = 6 + 3 = 9 unit squares.
So, area of shape (a) = area of shape (b). Both have equal area.
Page No. 151-153
Let Us Do
Q1: Find the area of your classroom floor in square meters. Take the help of your teacher to measure the length and breadth of the floor. What is the perimeter of the classroom floor?
Ans: Do it yourself.
Q2: Find the area and perimeter of the following shapes.
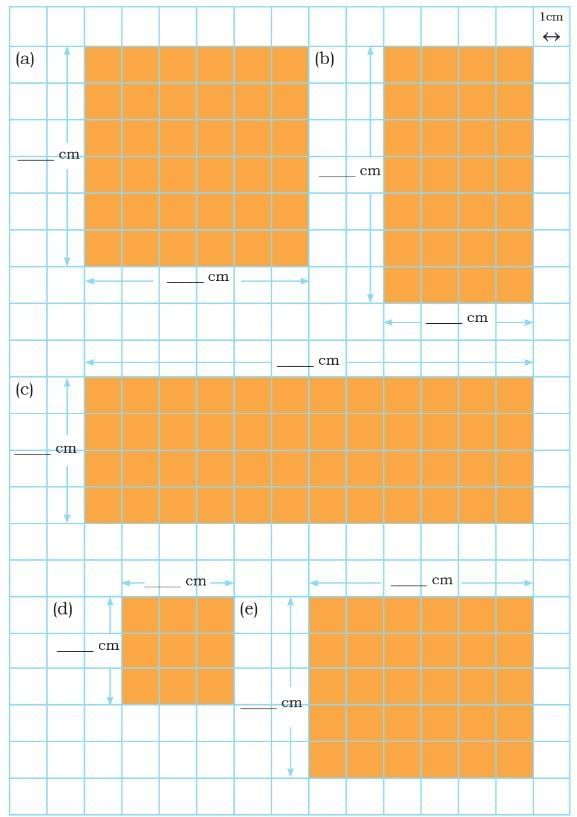
Ans:
(a) Side of the square = 6 cm.
Area = Length × Length
= 6 × 6
= 36 square cm.
Perimeter = 4 × Length
= 4 × 6
= 24 cm.
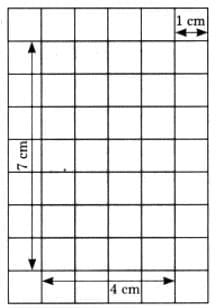
(b) Length = 4 cm, Breadth = 7 cm.
Area of a rectangle = Length × Breadth
= 4 × 7
= 28 square cm.
Perimeter of a rectangle = 2(Length + Breadth)
= 2 × (4 + 7)
= 2 × 11
= 22 cm.
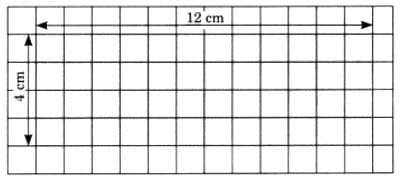
(c) Length = 12 cm, Breadth = 4 cm.
Area of a rectangle = Length × Breadth
= 12 × 4
= 48 square cm.
Perimeter of a rectangle = 2(Length + Breadth)
= 2 × (12 + 4)
= 2 × 16
= 32 cm.
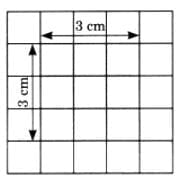
(d) Side of the square = 3 cm.
Area of a square = Side × Side
= 3 × 3
= 9 square cm.
Perimeter of a square = 4 × Side
= 4 × 3
= 12 cm.
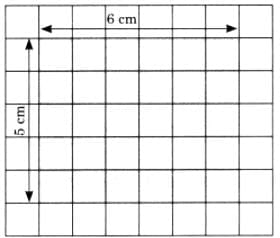
(e) Length = 6 cm, Breadth = 5 cm.
Area of a rectangle = Length × Breadth
= 6 × 5
= 30 square cm.
Perimeter of a rectangle = 2(Length + Breadth)
= 2 × (6 + 5)
= 2 × 11
= 22 cm.
Q3: Find the area and perimeter of the following objects. Use a scale or measuring tape to find the length and the breadth of each of the objects.
Ans: Do it yourself.
Q4: Find the area of a rectangular field whose length is 42 m and breadth is 34 m.
Ans:
Length = 42 m, Breadth = 34 m.
Area of a rectangle = Length × Breadth
= 42 × 34
= 1,428 square m.
Therefore, the area of the rectangular field is 1,428 square m.
Q5: The area of a rectangular garden is 64 square m and its length is 16 m. What is its breadth?
Ans:
Area = 64 square m, Length = 16 m.
Area = Length × Breadth
64 = 16 × Breadth
Breadth = 64 ÷ 16 = 4 m.
Therefore, the breadth of the rectangular garden is 4 m.
Q6: Find the area of the following figure with the dimensions as marked in the figure.
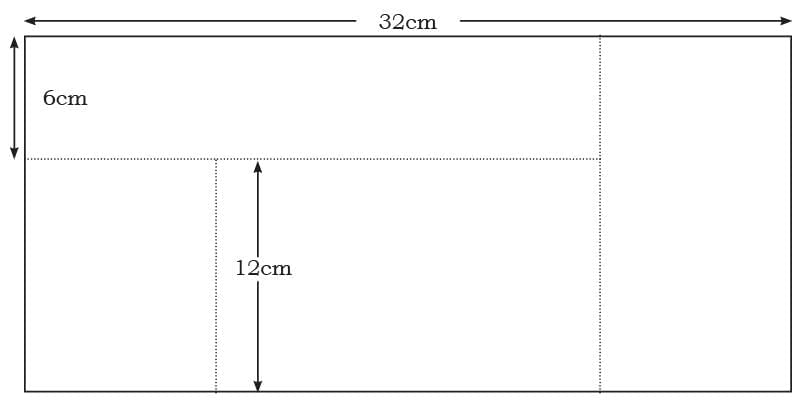
Ans:
Length = 32 cm.
Breadth = (6 + 12) cm = 18 cm.
Area of the rectangular figure = Length × Breadth
= 32 × 18
= 576 square cm.