Question 1. Look at the adjoining figure. If O is the center of the circle. PQ=12cm and ST = 3 cm, then find the radius of the circle when RS ⊥ PQ. Solution: Let us join O and P such that OP = r.
∵ RS ⊥ PQ
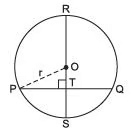∴ T is the mid-point of PQ
.⇒ PT = (1/2) PQ⇒ PT = (1/2) x 12 cm = 6 cm [∵ PQ = 12 cm (Given)]
And ∠ OTP = 90°
Also OS = r and TS = 3 cm
∴ OT = OS – TS = (r – 3) cm
Now, in right ΔOTP, we have OP2 = PT2 + OT2
⇒ r2 = 62 + (r – 3)2
⇒ r2 = 36 + r2 + 9 – 6r
⇒ 6r = 45
⇒ r =(45/6) = (15/2) = 7.5 cm
Thus, the radius of the circle is 7.5 cm.
Question 2. An equilateral triangle ABCABC is inscribed in a circle. Each side of the triangle is 99cm. Find the radius of the circle.
Solution: Let ABC be an equilateral triangle such that AB = BC = AC = 9 cm (each)
Let us draw a median AD corresponding to BC.
∴ BD =(1/2) BC
⇒ BD = (1/2) x 9 cm = (9/2)cm
Also, AD ⊥ BC [∵ O is the centre of the circle]
Now, in right ΔADB,
AD2 = AB2 – BD2
Since, in an equilateral triangle, the centroid and circumcentre coincide.
∴ AO: OD = 2:1
⇒ 
⇒ Radius = 3√3 cm
Thus, the required radius = 3√3 cm