Introduction
Today, let’s explore how we add and take away numbers, and why these are super useful.
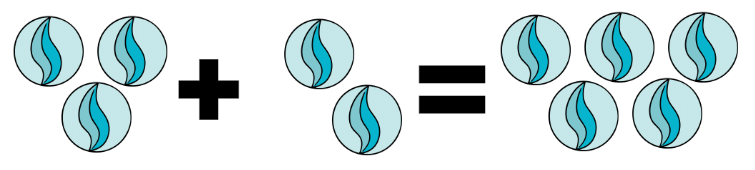
Addition is like putting things together. Imagine you have a pile of marbles. If you add more marbles to that pile, you end up with a bigger pile. For example, if you have 3 marbles and you add 2 more marbles, you will have 3 + 2 = 5 marbles in total.
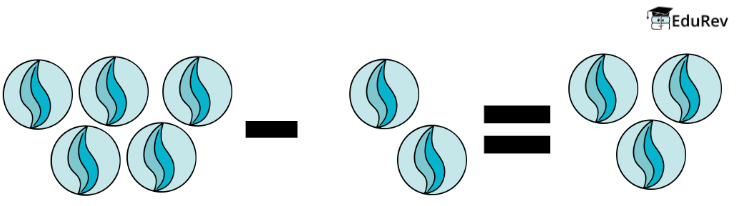
Subtraction is like taking things away. Let’s go back to our marbles. If you have 5 marbles and you take away 2 marbles, you will have 5 – 2 = 3 marbles left.
So, addition makes things bigger by adding more, and subtraction makes things smaller by taking away. They’re like the opposite of each other!
Try yourself:
What does addition do to a number?
- A.Makes it smaller
- B.Makes it bigger
- C.Keeps it the same
- D.None of the above
View Solution
Learn with Story- Addition & Subtraction

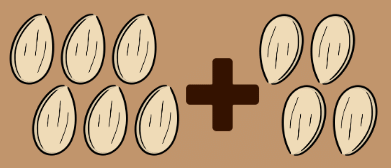
Once upon a time, there were two kids named Suman and Aditya. They had six plant seeds that they wanted to plant in their garden. So, they decided to ask their grandpa for help.
- Grandpa was very happy to see the kids doing something good, so he gave them four more seeds.
- This is like adding because now they had 6 + 4 = 10 seeds in total.
- Excitedly, Suman and Aditya went to their garden.
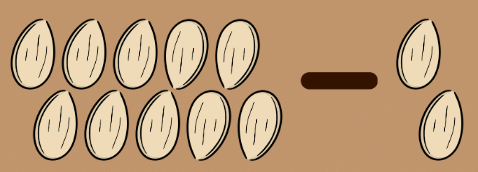
- They first planted two seeds next to the mango tree.
- Now, they had 10 – 2 = 8 seeds left.
- Then, they planted four seeds near the flowers.
- Subtracting these, they had 8 – 4 = 4 seeds left.
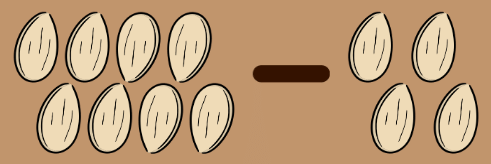
- Finally, they planted the remaining four seeds near the lemon tree.
- This left them with 4 – 4 = 0 seeds, which meant they had used up all their seeds.

The kids were so happy to see their garden full of newly planted seeds, all thanks to their teamwork and Grandpa’s help!
Try yourself:What is the result of adding 7 and 5?
- A.12
- B.11
- C.13
- D.14
View Solution
Tens Frame

A tens frame is a simple math tool used to understand numbers in groups of ten. It consists of a rectangular frame with ten boxes or squares arranged in rows of five. Each box can hold one object, like a counter or a dot.
Addition using Tens Frame
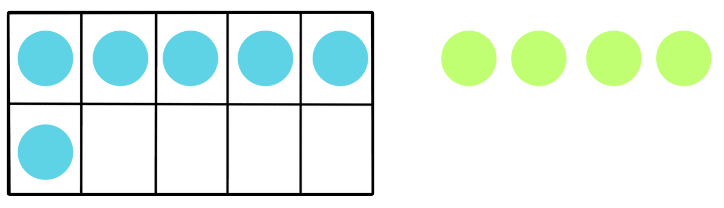
Let’s say you have a tens frame with 6 counters placed in it.
- This means that 6 out of the 10 boxes are filled, and there are 4 empty boxes.
- Now, if you add 4 more counters to the tens frame, you’ll fill up the remaining 4 empty boxes.

- Counting all the counters, you’ll find that there are now 6 + 4 = 10 counters in total, filling the entire tens frame.
Subtraction using Tens Frame

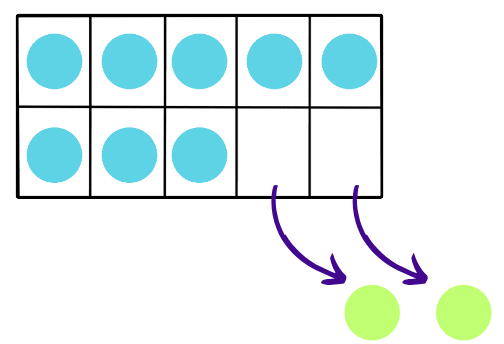
Starting with a full tens frame of 10 counters, each box containing one counter, if you take away 2 counters, you’ll remove them from the filled boxes.
- Now, you’ll have 8 counters remaining, filling 8 out of the 10 boxes on the tens frame.
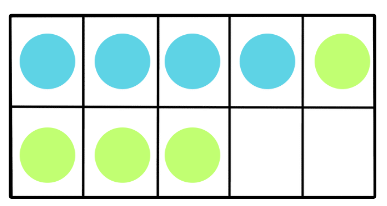
- Continuing with subtraction, if you take away 4 more counters, you’ll remove them from the filled boxes. Now, you’ll have 4 counters remaining, filling only 4 out of the 10 boxes on the tens frame.
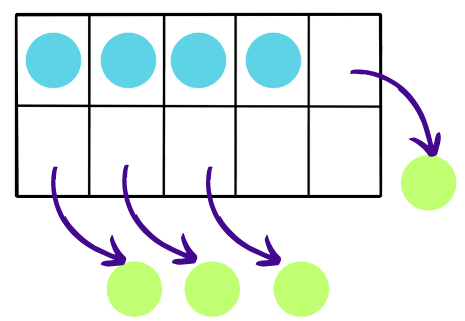
- Finally, if you take away the last 4 counters, you’ll remove them from the filled boxes, leaving the tens frame completely empty with 0 counters.
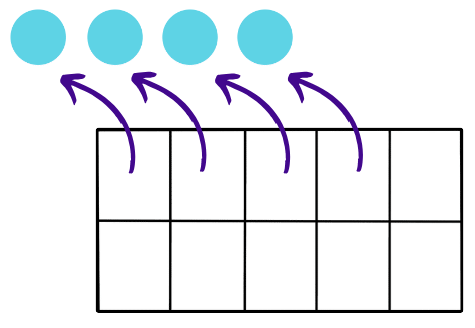
- Using the tens frame helps us see how adding fills up spaces, and subtracting takes away from those filled spaces, making it easier to understand addition and subtraction with numbers.
Try yourself:
In a tens frame with 8 counters placed, how many more counters are needed to fill it completely?
- A.2 counters
- B.10 counters
- C.5 counters
- D.3 counters
View Solution
Learn with Story- Using Number Line

Once upon a time, two kids named Maya and Arjun were sitting together, trying to solve a math problem that involved adding numbers bigger than 10.
- They had a tens frame in front of them, which they were using to understand smaller numbers easily.
- However, when it came to bigger numbers like 24 + 32, they started feeling confused.
- Just then, their elder brother Rahul walked into the room.

- Seeing their puzzled faces, Rahul asked what they were working on.
- Maya and Arjun explained that they were trying to add 24 and 32 using the tens frame but were finding it difficult.
- Rahul smiled and said, “Let me show you an easier way to do this using a number line.”
- He drew a long line on a piece of paper and marked 24 on it.
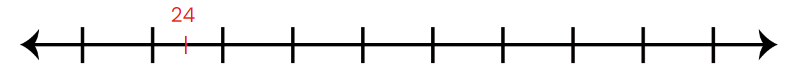
- “First, we start with 24,” Rahul explained. “Now, to make it easier, let’s add 6 steps to reach 30.” He marked 30 on the number line.

- “Next,” Rahul continued, “we add 10 more steps to reach 40.”
- He marked 40 on the number line. “Then, another 10 steps to reach 50,” he added, marking 50 on the line.
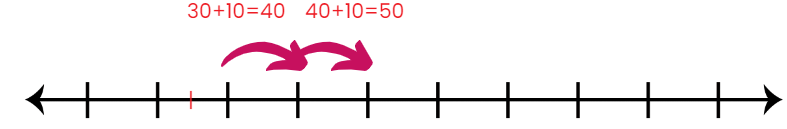
- “Finally, we add the remaining 8 steps to reach 58, which is our answer.”
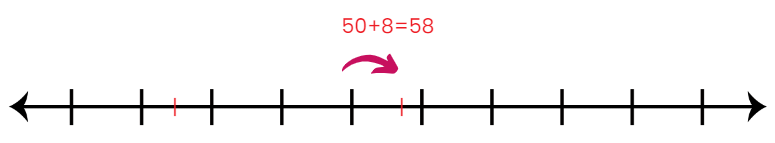
- Maya and Arjun looked amazed.
They could visually see each step of adding, making the process less confusing and more enjoyable.
Using number lines makes calculations easy because it breaks down the process into smaller, manageable steps that are visually represented. This helps in understanding the concept of addition or subtraction by visually seeing the progression of numbers, making it less daunting and more intuitive for learners.
Now, let’s help Arjun and Maya in subtracting 22 from 54 using the same method of the number line:
- Start with 54 on the number line.

- Subtract 10 to reach 44.

- Subtract 10 more to reach 34.

- Subtract 2 more to reach 32.
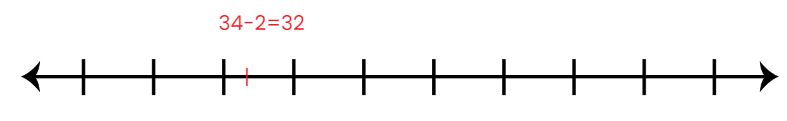
So, 54 – 22 = 32.
From that day on, Maya, Arjun, and Rahul always used the number line for bigger calculations, finding it to be a helpful and fun way to solve math problems.
Try yourself:
What is the missing number in the grid below?
Grid:
1 4 ?
2 5 8
3 6 9
- A.7
- B.10
- C.11
- D.12
View Solution
Number Grid
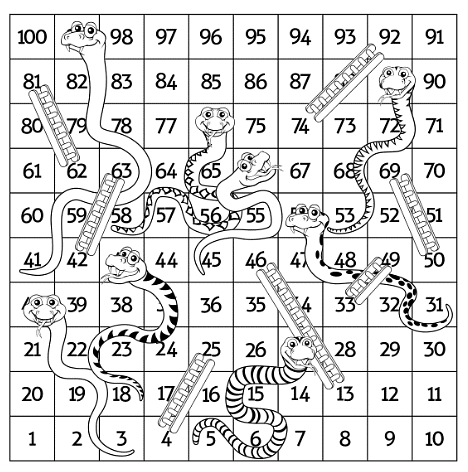
A number grid is like a map of numbers arranged in rows and columns. It’s similar to the grid used in games like Snake and Ladders, where each square in the grid contains a number.
For example, a number grid from 1 to 100 would have 10 rows and 10 columns, with numbers ranging from 1 to 100 distributed across the grid.
- Using a number grid can help us visualize and understand mathematical operations like addition, subtraction, and movement in a structured way. Let’s take the example you mentioned:
- If we start at 8 on the number grid and move 2 steps up, we land on 28. This is because each step up in the grid adds 10 to the number. So, from 8, going up 2 steps means adding 10 twice (8 + 10 + 10 = 28).
- Similarly, if we start at 28 and move 2 steps to the right, we land on 30. This is because each step to the right adds 1 to the number. So, from 28, moving right 2 steps means adding 1 twice (28 + 1 + 1 = 30).
- Conversely, if we move to the left, each step subtracts 1 from the number. For example, if we start at 30 and move 2 steps to the left, we land on 28 (30 – 1 – 1 = 28).
In this way, a number grid helps us visualize and perform calculations by understanding the patterns of addition and subtraction associated with movement in different directions on the grid. It’s a useful tool for learning and practicing mathematical operations in a structured and interactive manner.
Solving Puzzle- Magic Sum
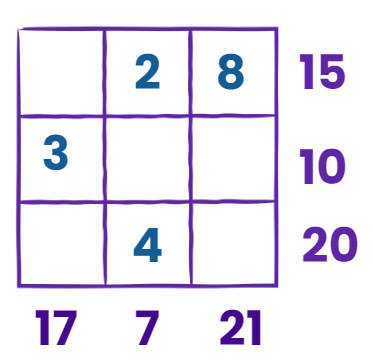
Imagine you have a 3×3 grid, like a small square divided into 3 rows and 3 columns. Each box in the grid has a number in it, but some boxes are blank. You also know the total sum for each row and column.
Let’s solve it step by step:
Horizontal Sum
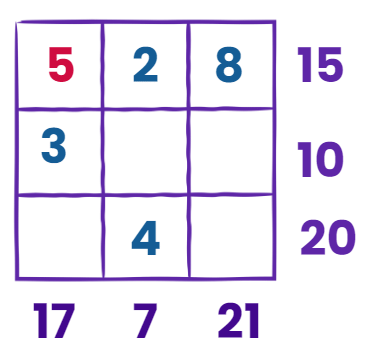
- First row: The given sum is 15, and you have 2 and 8 already. Adding them gives 10, so the blank box should be 15 – 10 = 5.
- Second row: The given sum is 10, and you have 3 already. Subtracting 3 from 10 gives 7 for the first blank box. Then, the second blank box must be 0 to make the sum correct.
- Third row: The given sum is 20, and you have 4 already. Subtracting 4 from 20 gives 16 for the first blank box. Then, the second blank box must be 0.
Vertical Sum
- First column: The given sum is 17, and you have 3 already. Subtracting 3 from 17 gives 14 for the first blank box. Then, the second blank box must be 0.
- Second column: The given sum is 7, and you have 2 already. Subtracting 2 from 7 gives 5 for the blank box.
- Third column: The given sum is 21, and you have 7 already. Subtracting 7 from 21 gives 14 for the first blank box. Then, the second blank box must be 0.
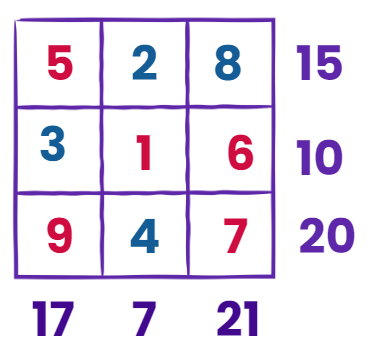
So, the completed grid looks like this:
Now that we’ve learned how to add, subtract, and solve grid puzzles with bigger numbers, let’s keep practicing getting even better at math!
Try yourself:
What is the result of 37 – 15?
- A.22
- B.20
- C.18
- D.14
View Solution
Bundle
- A bundle is a group or collection of items put together.
- In mathematics, we often make bundles to count more easily.
- A common example is bundling 10 sticks.

- Together to form one group or bundle of 10.

Why Do We Use Bundles?
- Helps in counting large numbers.
- Easy to count when we group things in bundles, especially in tens.
- It helps in understanding place value(tens and ones).
Example:
Suppose you have 14 pencils.
- First, make a bundle of 10 pencils.
- Then, you will have 1 bundle of 10 pencils and 4 loose pencils left.
- So, 14 pencils = 1 bundle of 10 + 4 pencils.

Counting in 10s:
10, 20, 30, 40, 50, 60, 70, 80, 90, 100.
Example: You have 10 apples in a basket. If Nani Maa adds 10 more apples each time, how many apples will you have after counting by 10s?
- Start with 10 apples.
- Add 10 more to get 20 apples.
- Add 10 more to get 30 apples.

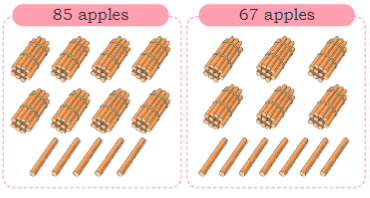
Let’s do Addition to find total number of sticks:
85 sticks + 67 sticks = Total 152 sticks
Nisha and Nandni both collected sticks. Who collected more Nisha or Nandni? How much more?
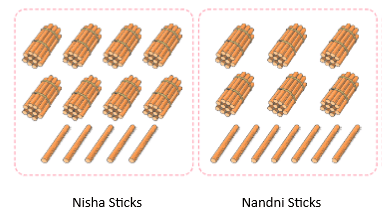
Total no of Nisha’s stick = 85
Total no of Nandni’s stick = 67
85 sticks – 67 sticks = 18 sticks
Nisha collected 18 sticks more than Nandni.
Try yourself:Raju sold 45 books on Monday and 68 books on Tuesday. How many books did he sell in two days?
- A.103 books
- B.113 books
- C.120 books
- D.23 books
View Solution
We practiced our math skills while playing games and enjoyed every moment with our family. Nani’s house was a special place where numbers and fun came together, making each day an exciting new lesson.
Until next time, keep counting, keep learning, and remember that every day can be an exciting new math adventure!