1. We the Travellers — I – Textbook Solutions

Reading and writing large numbers

Page 1, 3, 4

Imagine you have a lot of things, like thousands of candies! How do we write such big numbers?
Let’s start with 1,000.
What numbers do we get when we keep adding a thousand?
If we keep adding 1,000, we get these numbers

Let us see how we write numbers beyond 10,000 and how we name them. We write them in the same way as numbers below 9,999.

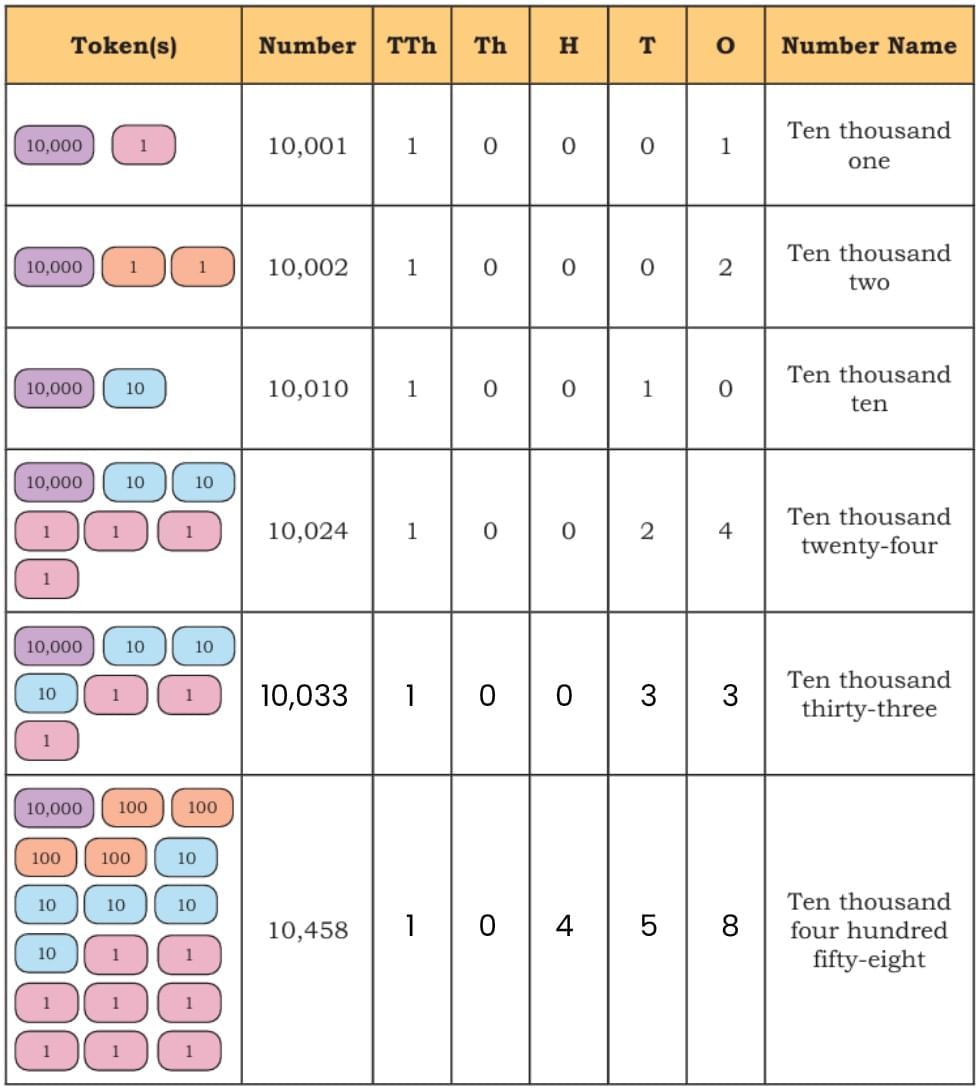
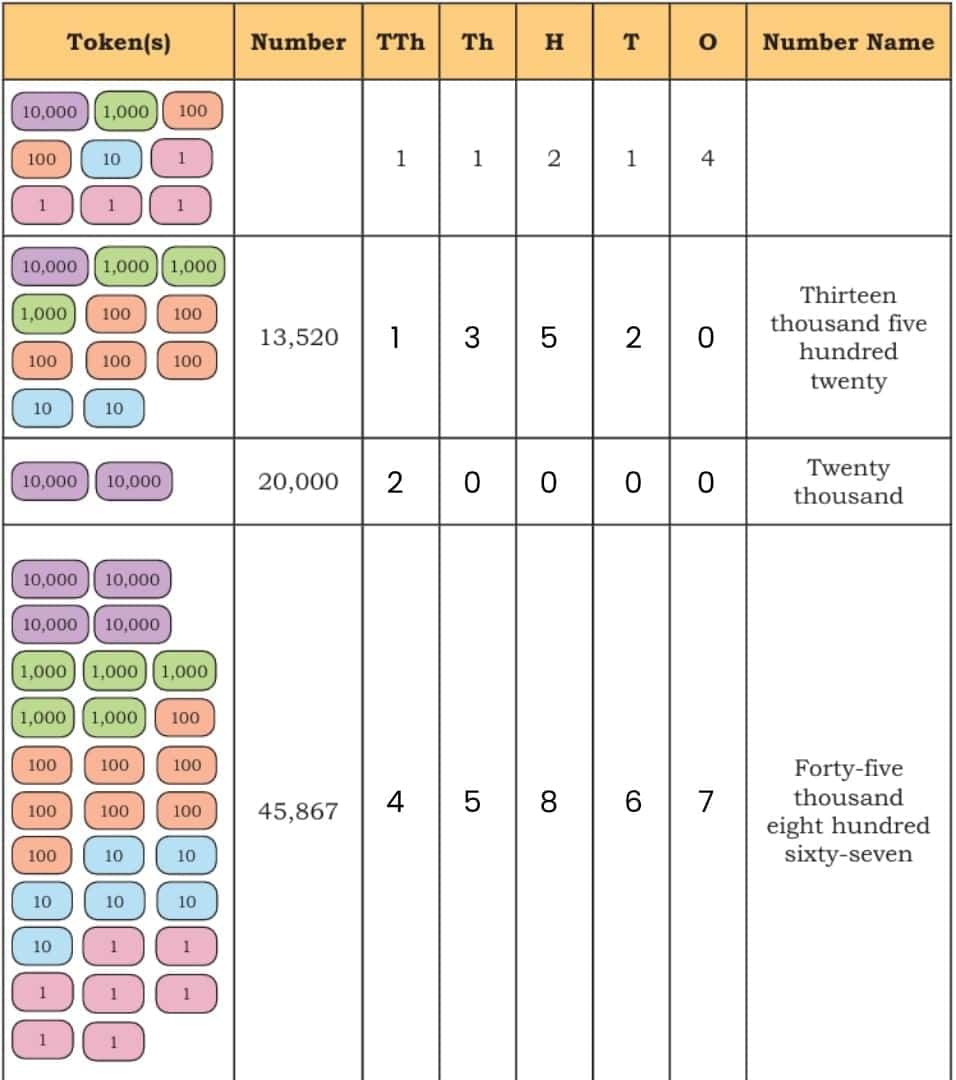
Let Us Do

Page 5, 6

Fill in the blanks by continuing the pattern in each of the following sequences. Discuss the patterns in class.
- (a) 456 567 678
- (b) 1,050 3,150 4,200
- (c) 5,501 6,401 7,301
- (d) 10,100 10,200 10,300
- (e) 10,105 10,125
- (f) 10,992 10,993
- (g) 10,794 10,796 10,798
- (h) 73,005 72,004
- (i) 82,350 83,350
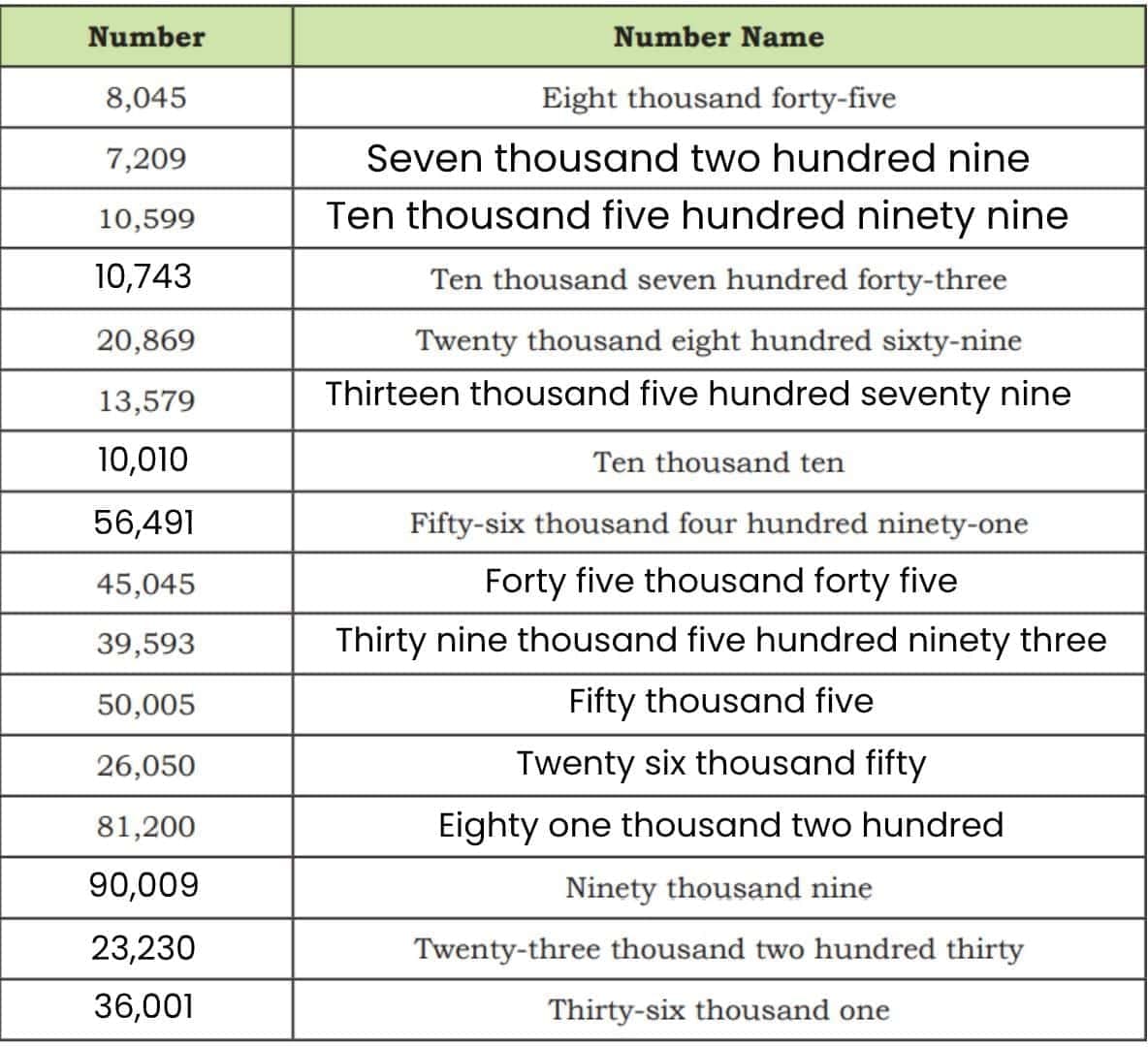
Fill in the blanks appropriately. Use commas as required.

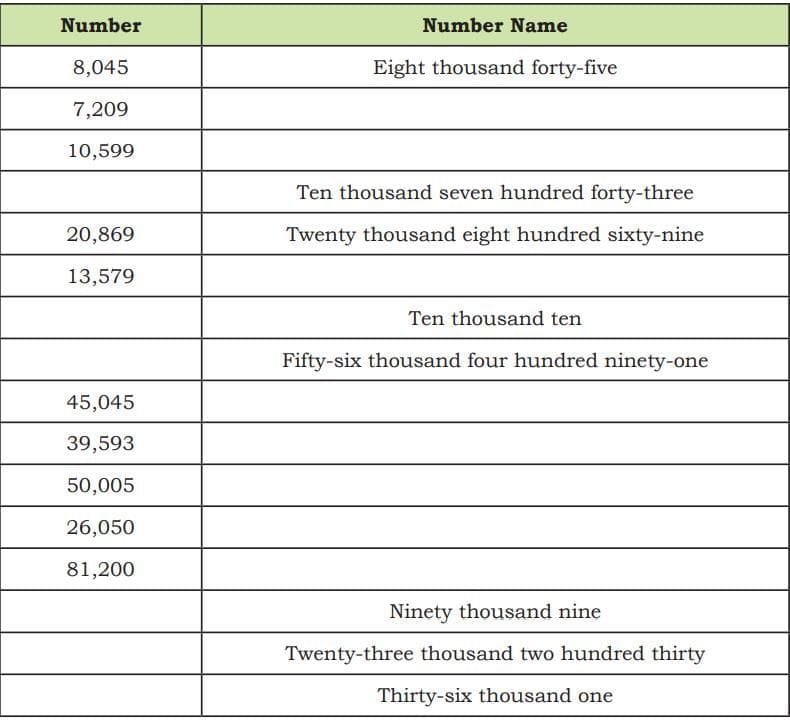
Answer:

2. Arrange the numbers below in increasing order. You can use the number line below if required.

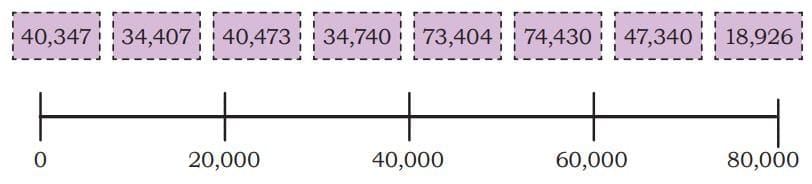
Answer:

4. A student said 9,990 is greater than 49,014 because 9 is greater than 4. Is the student correct? Why or why not?

Answer:

The student is not correct.

Here’s why:

When comparing two numbers, you must compare their place values starting from the left (the highest place value). Let’s break it down:

9,990 has 4 digits.
49,014 has 5 digits.

Any 5-digit number is always greater than any 4-digit number, regardless of what digits they start with.

Use the number line below to find the position of the numbers. Fill in the blanks.

Answer:

5. Digit swap

(a) In the number 1,478, interchanging the digits 7 and 4 gives 1,748. Now, interchange any two digits in the number 1,478 to make a number that is larger than 5,500

Answer:

The original number is 1,478.

To make the largest possible number, swap the digits so the biggest digit is in the thousands place. The digits are 1, 4, 7, 8. The largest arrangement is 8,741 (swap 1 and 8).

8,741 is much greater than 5,500.
So, you can swap the digits 1 and 8.

Any swap putting 7 or 8 in the leftmost place will create a number larger than 5,500 (such as 7,418, 8,471, etc.).

(b) Interchange two digits of 10,593 to make a number i) Between 11,000 and 15,000. ii) More than 35,000.

Answer:

i) Between 11,000 and 15,000

You need a five-digit number that starts with 11, 12, 13, or 14.

Try swapping 0 and 1: 01,593 (still 1,593 — not enough digits).
Try swapping 1 and 5: 50,193 (too large).
Swap 0 and 5: 15,093 (matches the condition).

Swapping 0 and 5 gives: 15,093 (which is between 11,000 and 15,000).

ii) More than 35,000

You’d need 3 or higher in the ten-thousand place.

Try swapping 1 and 3: 30,591 (less than 35,000).
Swap 1 and 5: 50,193 (greater than 35,000).

Swapping 1 and 5 gives: 50,193.

(c) Interchange two digits of 48,247 to make a number i) As small as possible. ii) As big as possible

Answer:

i) As small as possible

You want the smallest possible digit (other than 0, which is not present) in the highest place.

Swapping 4 and 2: 28,447 (2 in the ten-thousands place).

28,447 is the smallest possible by swapping 4 and 2.

ii) As big as possible

Largest digit in leftmost place. The digits are 4, 8, 2, 4, 7; largest is 8.

Swap 4 and 8: 84,247.

84,247 is the biggest possible by swapping 4 and 8.

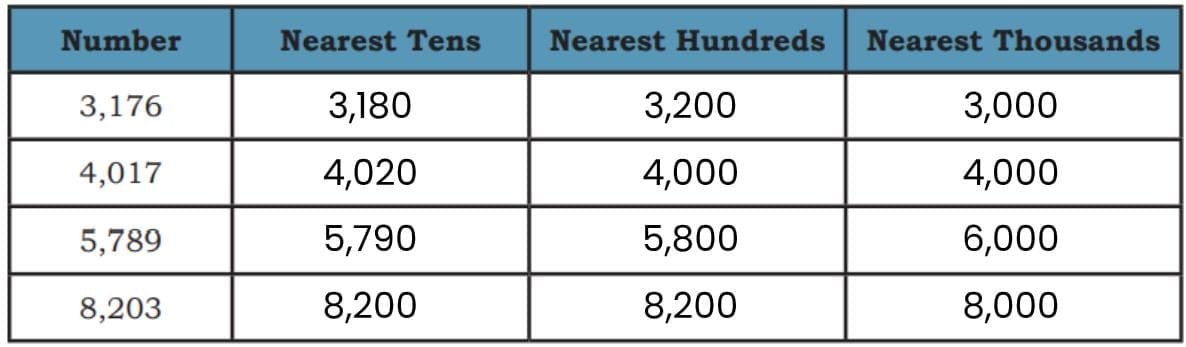
Nearest Tens (10s), Hundreds (100s), and Thousands (1,000s)

Page 8

Fill in the boxes appropriately.

Let Us Think

Page 8

1. Vijay rounded off a number to the nearest hundred. Suma rounded off the same number to the nearest thousand. Both got the same result. Circle the numbers they might have used.

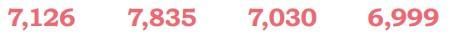
Answer:

This is because all these three numbers are closest to 7,000.

2. Think and write two numbers that have the same

(a) Nearest ten.
(b) Nearest hundred.
(c) Nearest thousand.

Answer:

(a) Nearest ten:
Any two numbers between the same pair of tens will round to the same ten.
Example: 42 and 47

Both rounded to nearest ten = 40 (since digits in ones place <5 for 42 and ≥5 for 47, so 47 rounds to 50. For SAME value: use 42 and 44, both round to 40).

So, 42 and 44 → Nearest ten = 40.

(b) Nearest hundred:
Any two numbers within the interval of 100 that round to the same hundred.
Example: 163 and 187

Both round to nearest hundred = 200 (163 rounds to 200 because tens digit is 6 (≥5); 187 rounds to 200). To get SAME, you want both under 150, say 121 and 149 → Both round to 100.

So, 121 and 149 → Nearest hundred = 100.

(c) Nearest thousand:
Any two numbers from 3,000 up to 3,499 will round to 3,000.
Example: 3,254 and 3,492

3,254 → 3,000
3,492 → 3,000

3. Think and write the numbers that have the same

(a) Nearest ten and nearest hundred.
(b) Nearest hundred and nearest thousand.
(c) Nearest ten, hundred and thousand.

Answer:

(a) Nearest ten and nearest hundred:
Pick numbers whose tens and hundreds digits are the same after rounding.
Example: 145 and 149

145 rounds to 150 (ten) and 100 (hundred);
146 rounds to 150 (ten) and 100 (hundred);
But not matching. Instead, try numbers like 200 and 202 →
200 (ten: 200, hundred: 200)
202 (ten: 200, hundred: 200)
So, 200 and 202.

(b) Nearest hundred and nearest thousand:
Pick numbers that, after rounding to hundred, also round to the same thousand.
Example: 3,040 and 3,080

3,040 to nearest hundred = 3,000; nearest thousand = 3,000
3,080 to nearest hundred = 3,100; nearest thousand = 3,000
But for SAME: 3,010 and 3,020, both round to 3,000 (hundred: 3,000; thousand: 3,000).
So, 3,010 and 3,020.

(c) Nearest ten, hundred, and thousand:
Pick numbers at the lower end so all three round the same.
Example: 1,001 and 1,004

Rounds to 1,000 (ten, hundred, thousand).

So, 1,001 and 1,004.

Let Us Do

Page 10

1. A cyclist can cover 15 km in one hour. How much distance will she cover in 4 hours, if she maintains the same speed?

Answer:

If a cyclist can cover 15 km in one hour and maintains the same speed, in 4 hours she will cover:

Distance = Speed × Time
= 15 km/hour × 4 hours
= 60 km

So, she will cover 60 km in 4 hours.

2. A school has 461 girls and 439 boys. How many vehicles are needed for all of them to go on a trip using the following modes of travel? The numbers in the bracket indicate the number of people that can travel in one vehicle.

(a) Bicycle (2)
(b) Autorickshaw (3)
(c) Car (4)
(d) Big car (6)
(e) Tempo traveller (10)
(f) Boat (20)
(g) Minibus (25)
(h) Aeroplane (180)

Answer:

The total number of students = 461 (girls) + 439 (boys) = 900 students.

To find the number of vehicles needed for each mode, use the formula:
Number of vehicles = Total persons / Capacity per vehicle (and round up to the next whole number when necessary).

(a) Bicycle (2 per bicycle):
Number of vehicles = 900 / 2 = 450

(b) Autorickshaw (3 per rickshaw):
Number of vehicles = 900 / 3 = 300

(c) Car (4 per car):
Number of vehicles = 900 / 4 = 225

(d) Big car (6 per big car):
Number of vehicles = 900 / 6 = 150

(e) Tempo traveller (10 per traveller):
Number of vehicles = 900 / 10 = 90

(f) Boat (20 per boat):
Number of vehicles = 900 / 20 = 45

(g) Minibus (25 per minibus):
Number of vehicles = 900 / 25 = 36

(h) Aeroplane (180 per plane):
Number of vehicles = 900 / 180 = 5

Finding Large Numbers Around Us

Page 10

1. Find something in the classroom whose count is a— (i) 4-digit number. (ii) 5-digit number.

Answer:

(i) 4-digit number:

Number of pages in all the textbooks combined in a classroom can easily be a 4-digit number (for example, if there are 5 books of about 250 pages each, that’s 1,250 pages).
Number of chalk pieces used in a year can also be in the thousands.

(ii) 5-digit number:

Number of pencil shavings collected over a year by all students in a classroom.
Number of words written by students in their notebooks during a year can be over 10,000.

2. List some quantities whose count is a 4-digit or a 5-digit number in the context of— (i) A tree. (ii) Your village/town/city, or any other place of your choice.

Answer:

In the context of:

(i) A tree:

4-digit count: Number of leaves on a large tree (many trees have well over 1,000 leaves).
5-digit count: Number of flowers or fruits produced by a mature, flowering tree in a season (some large fruit trees or flowering trees can have 10,000+ flowers in full bloom).

(ii) Your village/town/city, or another place:

4-digit count:
- Number of houses or families in a small town or village.
- Number of streetlights in a medium city.
5-digit count:
- Population of many towns or small cities (e.g., a town with 15,000 people).
- Number of vehicles registered in a city.
- Number of books in a large public library.
- Number of school children in all schools combined in a mid-sized city.

Let Us Do

Page 13

Write 5 numbers between the numbers 23,568 and 24,234. ___________, ___________, ___________, ___________, and ___________

Answers: 23,600; 23,789; 23,920; 24,000; and 24,123.

Write 5 numbers that are more than 38,125 but less than 38,600. ___________, ___________, ___________, ___________, and ___________

Answers: 38,200; 38,300; 38,500; 38,450; and 38,555.

Ravi’s car has been driven for 56,987 km till now. Sheetal’s car has been driven 67,543 km. Whose car has been driven more? ________________.

Answer: Sheetal’s car.

The following are the prices of different electric bikes. Arrange the prices in ascending (increasing) order. ₹90,000 ₹89,999 ₹94,983 ₹49,900 ₹93,743 ₹39,999

Answer:
₹39,999; ₹49,900; ₹89,999; ₹90,000; ₹93,743; ₹94,983.

5. The following table shows the population of some towns. Arrange them in a descending (decreasing) order.

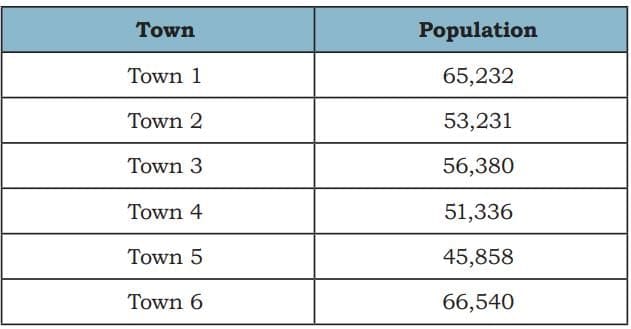
Answer:

Town 6: 66,540
Town 1: 65,232
Town 3: 56,380
Town 2: 53,231
Town 4: 51,336
Town 5: 45,858

6. Find numbers between 42,750 and 53,500 such that the ones, tens, and hundreds digits are all 0?

Answer:

These numbers would be the multiples of 1,000 in that range:
43,000; 44,000; 45,000; 46,000; 47,000; 48,000; 49,000; 50,000; 51,000; 52,000; 53,000

7. Write the following numbers in the expanded form. One has been done for you.

Answer:

(a) 783 = 700 + 80 + 3
(b) 8,062 = 8,000 + 0 + 60 + 2
(c) 9,980 = 9,000 + 900 + 80 + 0
(d) 10,304 = 10,000 + 300 + 0 + 4
(e) 23,004 = 20,000 + 3,000 + 0 + 0 + 4
(f) 70,405 = 70,000 + 0 + 400 + 0 + 5

8. Fill in the blanks with the correct answer. Share your thoughts in class.

(a) 983 = 90 Tens + 83 Ones

(b) 68 = 5 Tens + 18 Ones
Explanation: 5 tens = 50, 18 ones = 18; 50 + 18 = 68.

(d) 5,621 = 4 Thousand + 16 Hundreds + 2 Tens + 1 Ones
Explanation: 4 thousand = 4,000. 16 hundreds = 1,600. 2 tens = 20. 1 ones = 1.

Total: 4,000 + 1,600 + 20 + 1 = 5,621.

(e) 7,069 = 0 Thousand + 70 Hundreds + 69 Ones
Explanation: 70 hundreds = 7,000. 69 ones = 69. 0 thousands = 0. 7,000 + 69 = 7,069.

(f) 37,608 = 2 Ten Thousand + 17 Thousand + 608 Ones
Explanation: 2 ten thousands = 20,000. 17 thousands = 17,000. 608 ones = 608. 20,000 + 17,000 + 608 = 37,608.

(g) 43,001 = 4 Ten Thousand + 3 Thousand + 0 Hundreds + 1 Ones.

9. Fill in the blanks with the correct answers.

Answer:

(a) How many notes of ₹10 are there in ₹7,934?
793 (since 7934 ÷ 10 = 793 full notes, remainder ₹4)

(b) How many notes of ₹100 are there in ₹7,934?
79 (since 7934 ÷ 100 = 79 full notes, remainder ₹34)

(d) How many ₹500 notes are there in ₹7,934?
15 (since 7934 ÷ 500 = 15 full notes, remainder ₹434)

(e) How many notes of ₹10 are there in ₹65,342?
6,534 (since 65342 ÷ 10 = 6,534 full notes, remainder ₹2)

(f) How many notes of ₹100 are there in ₹65,342?
653 (since 65342 ÷ 100 = 653 full notes, remainder ₹42)

(g) How many thousands are there in 65,342?
65 (since 65342 ÷ 1000 = 65 full thousands, remainder ₹342)

(h) How many ₹500 notes are there in ₹65,342?
130 (since 65342 ÷ 500 = 130 full notes, remainder ₹342)