Introduction
- Numbers are like magic—they help us count, measure, and play games!
- Let’s explore the exciting world of numbers from 21 to 99 and discover how they can make everyday things even more fun.
- Ready to start this number adventure?

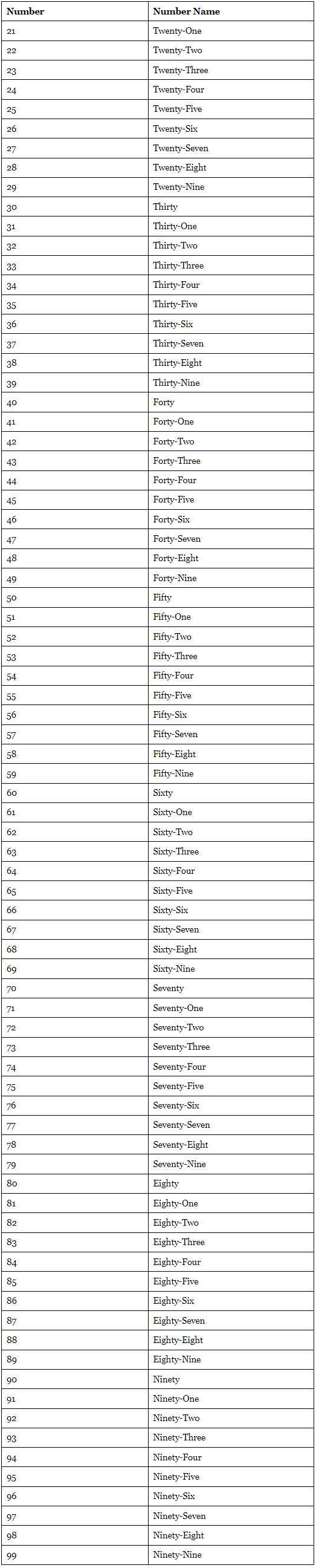
Number Names (21 to 99)
Let’s start by understanding the number names for each of these two-digit numbers:
Place Value (Tens and Ones)
- In a two-digit number, the first digit represents the tens place, and the second digit represents the ones place.
- For example, in the number 56, 5 is in the tens place, and 6 is in the ones place.
- Understanding place value helps us read and write numbers correctly.
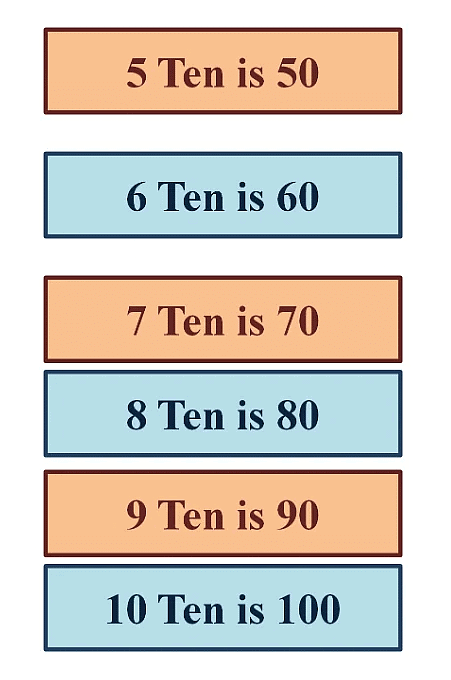
Counting (Skip Counting by Tens):
- We can count from 20 to 99 by adding 10 each time.
- For example, 20, 30, 40, 50, 60, 70, 80, 90.

Comparison of Numbers (Greater Than and Less Than)
- We can compare two two-digit numbers by looking at the digit in the tens place first.
- If the tens digits are different, the number with the greater tens digit is greater.
- If the tens digits are the same, we compare the ones digits to determine which number is greater.
- Examples:
45 and 63: Since 6 is greater than 4, therefore 63 is greater than 45.
78 and 74: Since 7 is the same in both numbers, we look at the ones place. 8 is greater than 4, so 78 is greater than 74.
Let’s Count!
Numbers 21 to 30 – Let’s Count
- Numbers 21 to 30 are formed by adding the tens place (20, 30) to the units place (1 to 10).
- For example, 21 is formed by adding 20 and 1, 22 is formed by adding 20 and 2, and so on.
- Practice counting from 21 to 30 to become familiar with these numbers.
Numbers 31 to 40 – One More Ten
- Numbers 31 to 40 follow a similar pattern.
- They are formed by adding the tens place (30) to the units place (1 to 10).
- For example, 31 is formed by adding 30 and 1, 32 is formed by adding 30 and 2, and so on.
- Practice counting from 31 to 40 to get comfortable with these numbers.
Numbers 41 to 50 – Moving Forward
- Numbers 41 to 50 are created by adding the tens place (40) to the units place (1 to 10).
- For example, 41 is formed by adding 40 and 1, 42 is formed by adding 40 and 2, and so on.
- Practice counting from 41 to 50 to reinforce your understanding.
Numbers 51 to 60 – Climbing Higher
- Numbers 51 to 60 continue the pattern.
- They are formed by adding the tens place (50) to the units place (1 to 10).
- For example, 51 is formed by adding 50 and 1, 52 is formed by adding 50 and 2, and so on.
- Practice counting from 51 to 60 to become proficient with these numbers.
Numbers 61 to 70 – A New Set
- Numbers 61 to 70 are formed by adding the tens place (60) to the units place (1 to 10).
- For example, 61 is formed by adding 60 and 1, 62 is formed by adding 60 and 2, and so on.
- Practice counting from 61 to 70 to strengthen your knowledge.
Numbers 71 to 80 – Further Exploration
- Numbers 71 to 80 follow the same pattern.
- They are formed by adding the tens place (70) to the units place (1 to 10).
- For example, 71 is formed by adding 70 and 1, 72 is formed by adding 70 and 2, and so on.
- Practice counting from 71 to 80 to become more confident.
Numbers 81 to 90 – Nearing the End
- Numbers 81 to 90 are created by adding the tens place (80) to the units place (1 to 10).
- For example, 81 is formed by adding 80 and 1, 82 is formed by adding 80 and 2, and so on.
- Practice counting from 81 to 90 to solidify your understanding.
Numbers 91 to 99 – The Final Stretch
- Numbers 91 to 99 follow the same pattern as the previous sets.
- They are formed by adding the tens place (90) to the units place (1 to 9, as there is no 0 in the units place).
- For example, 91 is formed by adding 90 and 1, 92 is formed by adding 90 and 2, and so on.
- Practice counting from 91 to 99 to master these numbers.
What is the Ones and Tens Concept?
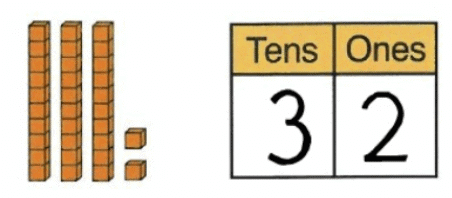
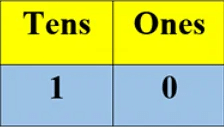
The number 10 is the first and the smallest two-digit number.
Example 1:
- Let’s take 10 pencils.

- Now make a group of 10 pencils.

- We can make only 1 group. It represents 1 Ten. But there is no single pencil remaining. It indicates 0 ones.
- So, the number 10 can write as:
Example 2:
- If we take 21 pencils, we can make 2 groups of 10 pencils that can be represented as 2 Tens.
- 1 remaining pencil can be represented as 1 Ones.
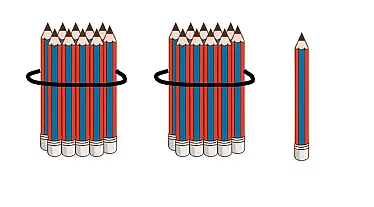
- 2 Tens and 1 Ones = 21
- We can write 21 as:
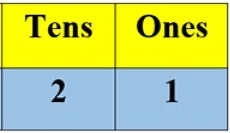 Example 3:
Example 3:
- We can represent 100 as 10 groups of Tens.
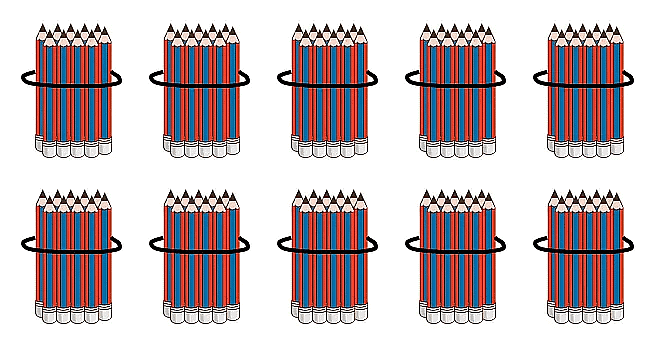
- We cannot write 100 as:
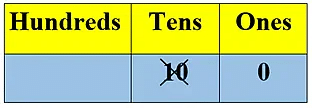
- We use the hundreds place. The number 100 is written as:

100 is the first and smallest three-digit number.
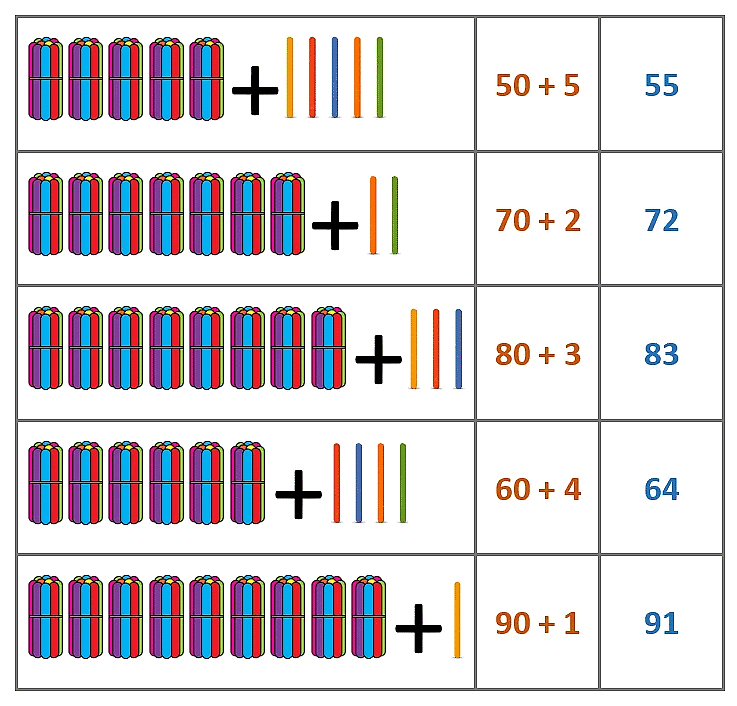
Let’s calculate the number of popsicles given in the table below
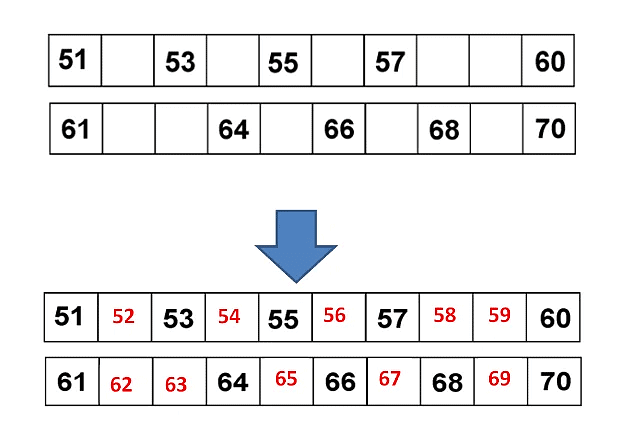
Missing Numbers
A series or sequence where a number is missed is known as a missing number sequence.
Look at the example given below.