Class 4th Mathematics ( Maths Mela ) Chapter Notes

Introduction

In this chapter, we will explore the fascinating world of large numbers, particularly focusing on thousands and how they relate to our daily lives. From counting people at community events to understanding place values, we’ll discover how numbers beyond 1000 are represented in the Indian number system.

Thousand Waterfall

Thousands of water droplets make up this magnificent waterfall – an example of thousands in nature

Let’s begin with a practical example!

• Jaspreet and Gulnaz are organizing a langar (community lunch) at their neighborhood Gurudwara. 
• They expect around one thousand (1000) people to attend. 
• Throughout the event, they keep track of how many people come at different times: 52 people, 145 people, 325 people and 508 people.Community lunch organised by Jaspreet and Gulnaz
• By the end of the day, they need to count how many people in total were served food. 

This requires understanding how to work with numbers in the hundreds and thousands.

Place Value System

The Indian number system, which was discovered in India around 2000 years ago, allows us to write all numbers using just ten symbols: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. This system is now used around the world!

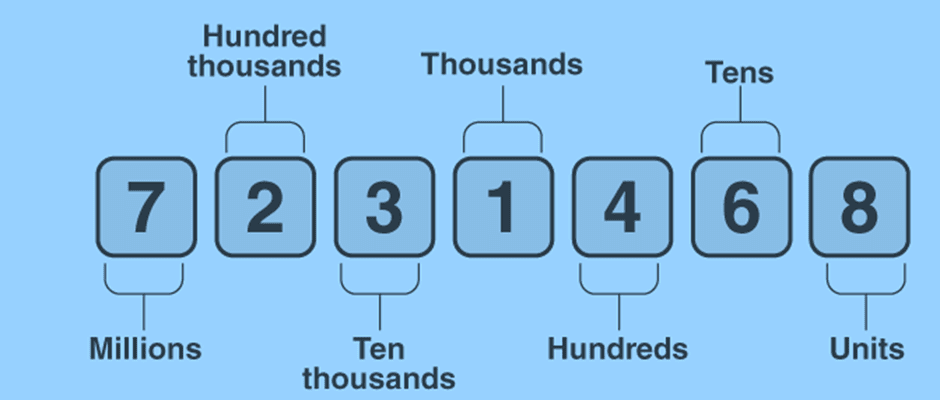
A place value chart helps us see how much each digit in a number is worth based on where it is located.

In the Indian system, numbers are grouped into hundreds, thousands, lakhs, crores, and so on. Here’s a breakdown:

• Units: The first three digits from the right are the units, tens, and hundreds.
• Thousands: The next two digits are the thousands.
• Lakhs: The next two digits are the lakhs.
• Crores: The digits after lakhs are the crores.

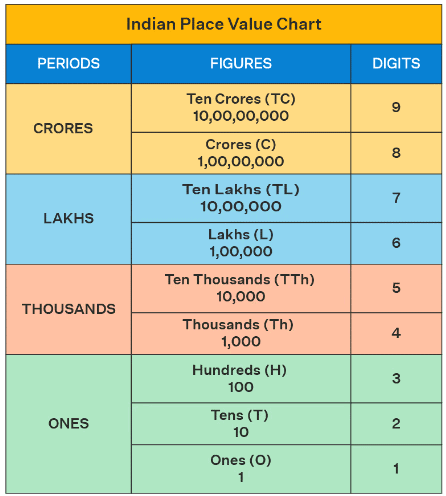
Indian Place Value Chart

Example 1: How can we break down the number 12,34,567 using the Indian place value system?
Sol: We break the number from right to left like this:

12,34,567 becomes:
12 (Lakhs), 34 (Thousands), 567 (Units)

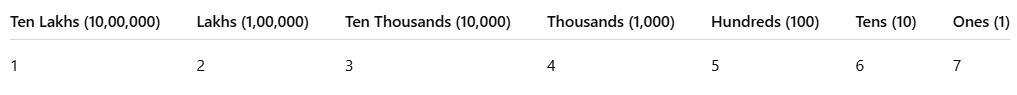
• 1 ten lakh = 10,00,000
• 2 lakhs = 2,00,000
• 3 ten thousands = 30,000
• 4 thousands = 4,000
• 5 hundreds = 500
• 6 tens = 60
• 7 ones = 7

So,
12,34,567 = 10,00,000 + 2,00,000 + 30,000 + 4,000 + 500 + 60 + 7

One Thousand(1000)

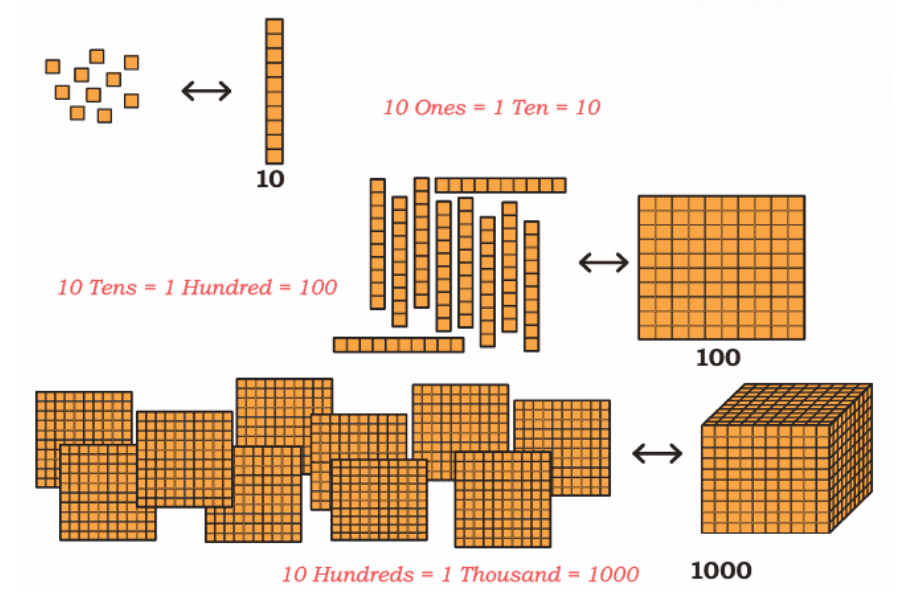
We can visualize numbers using Dienes Blocks (also known as Base-10 Blocks):

Place Value Dienes Blocks

Dienes blocks showing representation of numbers with ones, tens, hundreds, and thousands.

One (1) – represented by a small cube

Ten (10) – represented by a rod of 10 small cubes

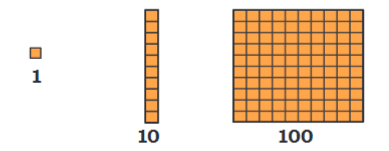
Hundred (100) – represented by a flat square of 10×10 small cubes

Thousand (1000) – represented by a large cube of 10×10×10 small cubes

This helps us understand the relationship between different place values:

10 Ones = 1 Ten

10 Tens = 1 Hundred

10 Hundreds = 1 Thousand

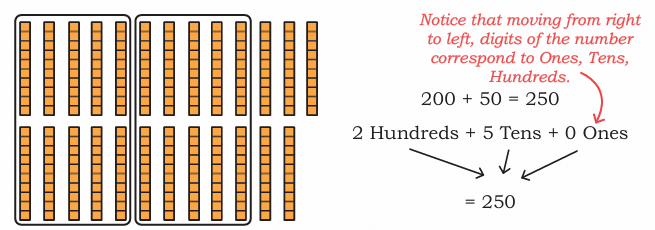
Grouping and Regrouping

1. When we have more than 9 in any place value, we need to regroup:

10 Ones → 1 Ten

10 Tens → 1 Hundred

10 Hundreds → 1 Thousand

2. Regrouping ones into tens and tens into hundreds using base 10 blocks

For example:

14 Ones = 1 Ten + 4 Ones

23 Ones = 2 Tens + 3 Ones

106 = 1 Hundred + 0 Tens + 6 Ones (or 10 Tens + 6 Ones)

Circle as many groups of 10 Ones or 10 Tens as possible. Write the final number against the following pictures.

a)

b)

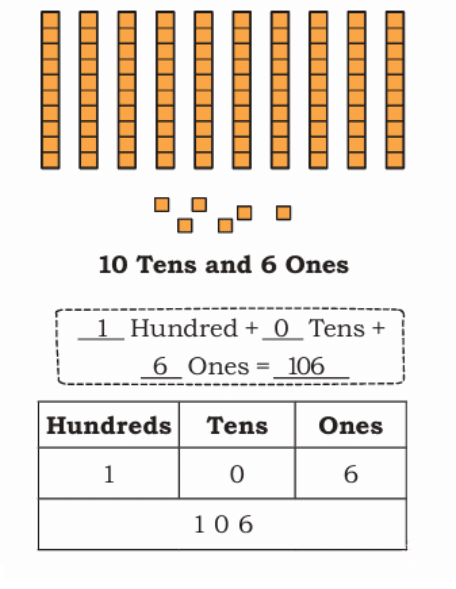
c)

Try yourself:

What do we call the next two digits after hundreds in the Indian number system?

• A.Lakhs
• B.Thousands
• C.Crores
• D.Tens

View Solution

Numbers Beyond 1000 ( One Thousand)

Let’s learn about big numbers — numbers that are more than 1000!

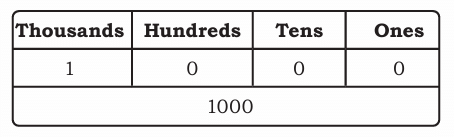
What is 1000?

• 1000 is made up of:
  • 1 Thousand
  • 0 Hundreds
  • 0 Tens
  • 0 Ones
    So, 1000 = 1 thousand + 0 hundred + 0 ten + 0 one

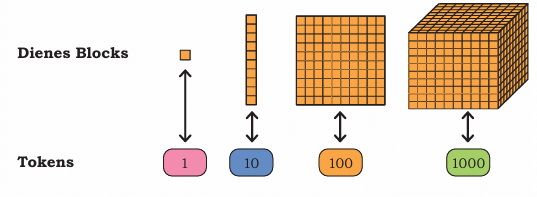
We use special blocks called Dienes Blocks to show numbers. But drawing big blocks is hard! So, we use tokens to show the same numbers.

Let’s Make the Number 1001

Look at this:

• We have 10 orange tokens of 100 each → 100 × 10 = 1000
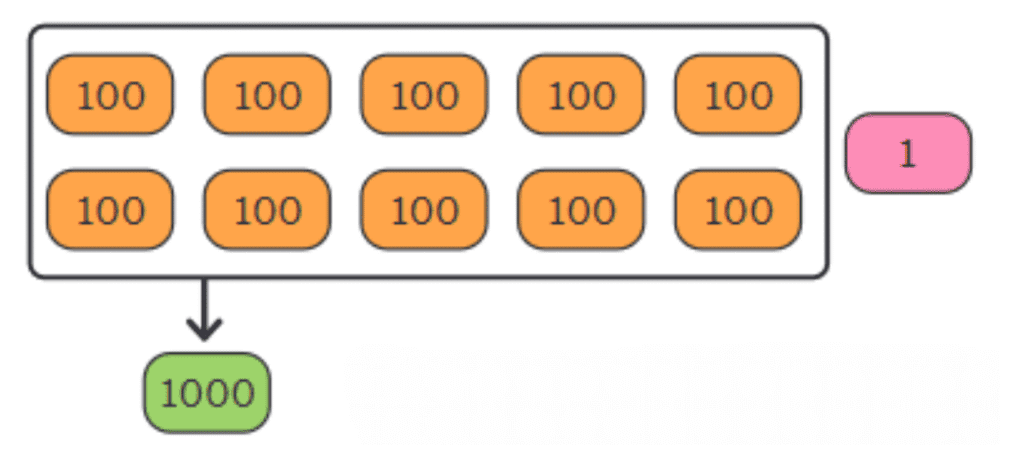• And 1 pink token → 1That means: 1000 + 1 = 1001

Let’s Write It in the Place Value Table:

1 Thousand + 0 Hundred + 0 Ten + 1 One = 1001

Comparing Numbers

Comparing numbers means looking at two numbers and finding out which one is greater, smaller, or if they are equal.

We use three special signs to compare:

1. Greater than ( > )
   Example: 7 > 5 (7 is bigger than 5)
2. Less than ( < )
   Example: 3 < 9 (3 is smaller than 9)
3. Equal to ( = )
   Example: 4 = 4 (Both numbers are same)

Let’s compare 3012 and 3102.

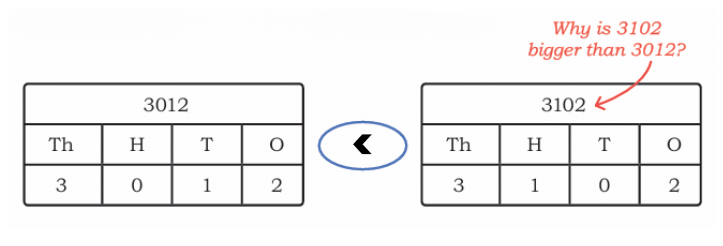
Thousands:
Both numbers have 3 thousands. So we go to the next digit.

Hundreds:

• 3012 has 0 hundreds
• 3102 has 1 hundred

Since 1 hundred is more than 0 hundreds,

So, 3102 > 3012

Try yourself:What do we get when we regroup 10 ones?A.1 TenB.1 HundredC.1 ThousandD.1 OneView Solution

Q1: Compare the numbers 425 and 452. Which one is larger?

Sol: Step 1: Both numbers have 3 digits, so we need to compare the digits.

Step 2: Compare the hundreds digit: Both have 4 in the hundreds place.

Step 3: Compare the tens digit: 2 in 425 and 5 in 452.

Since 5 > 2, we know that 452 > 425.

Therefore, 452 is larger than 425.

Q2: Arrange the numbers 789, 798, 879, 897, 978, 987 in ascending order (smallest to largest).

Sol: Ascending order means arranging numbers from the smallest to the largest.

Let’s arrange these numbers:789, 798, 879, 897, 978, 987

Step 1: Look at the Hundreds PlaceHundreds Place

All numbers start with 7, 8, or 9.

• 789 and 798 start with 7 → smallest group
• 879 and 897 start with 8
• 978 and 987 start with 9 → biggest group

Step 2: Compare numbers within each group

Group starting with 7:

• 789 < 798

Group starting with 8:

• 879 < 897

Group starting with 9:

• 978 < 987

Solved Examples

Example 1: Write the number 1,234 in expanded form and identify the place value of each digit.

Sol: Step 1: Identify the place value of each digit.

1 is in the thousands place

2 is in the hundreds place

3 is in the tens place

4 is in the ones place

Step 2: Write the expanded form by multiplying each digit by its place value.

1 × 1000 = 1000

2 × 100 = 200

3 × 10 = 30

4 × 1 = 4

Step 3: Add all the values to get the expanded form.

1,234 = 1000 + 200 + 30 + 4

Example 2: Arrange the numbers 1,025, 1,205, 1,052, and 1,520 in descending order (largest to smallest).

Sol: Step 1: Compare the thousands digit.

All numbers have 1 in the thousands place, so we need to compare the hundreds digit.

Step 2: Compare the hundreds digit.

1,025 has 0 in the hundreds place

1,205 has 2 in the hundreds place

1,052 has 0 in the hundreds place

1,520 has 5 in the hundreds place

Since 5 > 2 > 0, we know that 1,520 is the largest, followed by 1,205.

Step 3: For numbers with the same hundreds digit (1,025 and 1,052), compare the tens digit.

1,025 has 2 in the tens place

1,052 has 5 in the tens place

Since 5 > 2, we know that 1,052 > 1,025.

Step 4: Arrange all numbers in descending order:

1,520, 1,205, 1,052, 1,025

Example 3: Find the next three numbers in the pattern: 825, 850, 875, …

Sol: Step 1: Identify how the numbers change from one to the next.

From 825 to 850: The number increases by 25

From 850 to 875: The number increases by 25

Step 2: Apply the same pattern to find the next three numbers.

After 875, adding 25 gives us 900

After 900, adding 25 gives us 925

After 925, adding 25 gives us 950

So the next three numbers in the pattern are 900, 925, and 950.

By understanding these concepts, you can confidently work with larger numbers and apply this knowledge to solve real-world problems. Remember, mathematics is not just about numbers; it’s about understanding the patterns and relationships that help us make sense of the world around us.

Introduction

In this chapter, we will explore the fascinating world of patterns that surround us in our daily lives. From counting objects to arranging money, from identifying even and odd numbers to recognizing patterns in arrangements – patterns are everywhere!

Patterns help us organize information, make predictions, and solve problems more efficiently. They are the building blocks of mathematics and help us understand the world around us. Whether you’re counting coconut trees or arranging coins in groups, patterns make these tasks easier and more fun.

Coconut Trees arranged in a patternCoins in Patterns

Let’s dive into the world of patterns and discover how they shape our understanding of numbers and arrangements!

Let’s Begin with a Story

Let us Count – Raju’s Pattern Adventure

Raju loved to collect and organize things. One day, while helping his grandmother in the kitchen, he noticed something interesting about the way she arranged fruits in a basket.

“Grandmother, why do you always place the fruits in this circular pattern?” Raju asked.

His grandmother smiled and replied, “Patterns help us organize things better, Raju. Look at how I’ve arranged these fruits – one apple in the center, surrounded by eight oranges. This pattern not only looks beautiful but also helps me count them easily.”

Raju was fascinated. He began to notice patterns everywhere – in the arrangement of trees in the garden, in the design of floor tiles, and even in the way his teacher organized students for group activities.

Soon, Raju started creating his own patterns with different objects. He realized that patterns make counting easier and help us understand relationships between numbers.

Just like Raju, let’s explore various patterns in our daily life and learn how they help us understand mathematics better!

Patterns with Money

Money provides an excellent way to understand patterns and practice counting. Let’s explore some interesting money patterns.

Pattern 1: Flower Pattern with Coins

In this pattern, coins are arranged in a flower-like shape with one coin in the center and coins arranged around it.Flower – Shape Pattern

Pattern 2: Rectangle Pattern with Notes and Coins

In this pattern, notes and coins are arranged in a rectangular shape.

Rectangular Shape pattern

Try yourself:

What did Raju’s grandmother say about patterns?

• A.They help organize things better.
• B.They are only for counting money.
• C.They make everything look the same.
• D.They are not useful in daily life.

View Solution

Two Ways of Arranging Coins

Shirley and Shiv arranged their coins in the following ways. Let’s examine the number of coins in each arrangement.

Coin ArrangementsShirley’s Arrangement (Odd Numbers)

Shirley arranged her coins in groups of 3, 5, 7, etc. These are odd numbers.

Shiv’s Arrangement (Even Numbers)

Shiv arranged his coins in groups of 4, 6, 8, etc. These are even numbers.

This arrangement helps us understand the concept of odd and even numbers, which we’ll explore in more detail in the next section.

Even and Odd Numbers

Even Numbers

Look at the number 4 on the left side of the image. There are 4 ice cream cones.

We can divide them into two equal groups:

• 2 cones in one group
• 2 cones in the other group

That means 4 is an even number because it can be split equally into two groups with nothing left over.

So, Even numbers are numbers that can be divided into two equal parts.

Examples of even numbers: 2, 4, 6, 8, 10

Odd Numbers

Now look at the number 5 on the right side. There are 5 cupcakes.

When we try to divide them into two groups:

• 2 cupcakes go in one group
• 2 cupcakes go in the second group
• But 1 cupcake is left over

That means 5 is an odd number because it cannot be split into two equal groups without something being left out.

So, Odd numbers are numbers that cannot be divided equally into two parts.

Examples of odd numbers: 1, 3, 5, 7, 9

Try yourself:

What type of numbers did Shirley use to arrange her coins?

• A.Odd numbers
• B.Even numbers
• C.Prime numbers
• D.Fractional numbers

View Solution

Q1: Do you think all numbers in the times-2 table are even?

Sol: Yes, all numbers in the times-2 table are even numbers. This is because when we multiply any number by 2, we are essentially creating pairs, which is the definition of an even number.

For example:

1 × 2 = 2 (1 pair)

2 × 2 = 4 (2 pairs)

3 × 2 = 6 (3 pairs)

4 × 2 = 8 (4 pairs)

5 × 2 = 10 (5 pairs)

Sol: The times-3 table follows a pattern of odd, even, odd, even, and so on:

1 × 3 = 3 (odd)

2 × 3 = 6 (even)

3 × 3 = 9 (odd)

4 × 3 = 12 (even)

5 × 3 = 15 (odd)

This happens because when we multiply an odd number by 3, we get an odd number, and when we multiply an even number by 3, we get an even number.

Q2: Are there more even or odd numbers between 1 and 100?

Sol: Let’s analyze this systematically:

Even numbers between 1 and 100: 2, 4, 6, 8, …, 98, 100

Odd numbers between 1 and 100: 1, 3, 5, 7, …, 97, 99

Counting them:

Even numbers: 2, 4, 6, …, 98, 100 → 50 numbers

Odd numbers: 1, 3, 5, …, 97, 99 → 50 numbers

Therefore, there are an equal number of even and odd numbers between 1 and 100.

Sol: The possible 2-digit numbers are:

16 (which is even because it ends in 6)

61 (which is odd because it ends in 1)

Let’s Try!

This activity helps us understand that a number is even if its last digit is even, and a number is odd if its last digit is odd.

Some Solved Examples 

Example 1: Rahul has 5 ₹10 notes, 3 ₹5 coins, and 7 ₹2 coins. How much money does he have in total?

Sol: Amount from ₹10 notes = 5 × ₹10 = ₹50

Amount from ₹5 coins = 3 × ₹5 = ₹15

Amount from ₹2 coins = 7 × ₹2 = ₹14

Total amount = ₹50 + ₹15 + ₹14 = ₹79

Example 2: Sita has 45 candies. She wants to distribute them equally among her friends. Can she distribute them equally among 2 friends? What about 3 friends? Explain your reasoning.

Sol: For 2 friends:

45 ÷ 2 = 22 remainder 1

Since there is a remainder, she cannot distribute them equally among 2 friends.

For 3 friends:

45 ÷ 3 = 15 remainder 0

Since there is no remainder, she can distribute them equally among 3 friends, giving 15 candies to each friend.

This is because 45 is an odd number (not divisible by 2) but is divisible by 3.

Example 3: Observe the given pattern and draw the next three shapes in this pattern.

Sol:

This is an example of a repeating pattern with a cycle of 3 shapes.

Introduction

Imagine you’re playing a fun game of hide and seek with your best friends at school. You’re hiding under a table, behind the curtain, or maybe inside the cupboard. You’re trying hard not to giggle or make a sound!

Now suddenly, someone finds you!
You ask, “How did you see me?!”
They smile and say, “I was looking from the top!”

That’s right! Things look very different when we look at them from different sides—from the top, from the front, or from the side. Just like in video games or puzzles, where you have to look at the whole scene carefully to find clues.

This chapter is all about seeing and understanding the space around us in a fun and smart way! You will learn:

• The difference between a top view, side view, and front view of the same object. A book may look like a rectangle from the top, but just a line from the side!
• Using positions like left, right, top row, middle row, first column, etc., we’ll learn how to describe exactly where something is—just like giving clues in treasure hunts!
• How to use and draw maps and follow paths.

Views of Objects

• Objects can be seen from different angles: top view, front view, and side view.
• The same object looks different depending on the view.
• For example, a brick drawn by Mini, Bholu, and Rani looks different because each child drew a different view (top, front, or side).
• The top view (Bholu’s drawing) shows the shape from above, the front view (Mini’s drawing) shows the face from the front, and the side view (Rani’s drawing) shows the side of the object.

Example of a 3D Shape:

A 3D shape can be viewed from the top, from the side and from the front and these views can be combined to visualise what the solid looks like.
Thus, we see that a cuboid appears to be rectangle, when viewed from any direction. Now, let us see the different views of a car, which is a 3D shape.

Try yourself:

What is a top view of an object?

• A.The shape seen from above
• B.The face seen from the front
• C.The side seen from the left
• D.The back seen from behind

View Solution

Identifying Views

• Different objects can be recognized by their views.
• For example, a tree looks like a circle from the top and a triangle from the front.
• Drawings of objects like chairs, tables, pencils, erasers, and bottles show different shapes based on their views.

Example 1: Mini draws her water bottle from three views. Top view: Circle, Side view: Rectangle and Front view: Rectangle.

Ans: Mini’s bottle is shaped like a cylinder. Cylinders look like:

• A circle from the top
• A rectangle from the front and side

Try it Yourself!
 Take a matchbox or pencil box and draw it while looking at it from the top, front, and side. Each view gives a different picture!

Understanding Positions in a Grid What is a Grid?

A grid is a table made of rows and columns. It helps us show the position of objects clearly. Each square in the grid has its own place using:

• Rows (go left to right)
• Columns (go up and down)

We can use grids to give clues, draw objects, and find positions—just like in a game!

In this activity:

• One player hides a treasure (thinks of an object in the grid).
• The other player tries to find it by following clues and steps like:
  • “Take 2 steps up and 1 step left.”
  • “Now you are still 2 steps away!”

Grid Game

Here are the clues given by Rani to fill the grid:

• An eraser at the top right corner → That’s Row 3, Column 3
• A pencil in the top left corner → That’s Row 3, Column 1
• An apple in the middle of the second row and second column → That’s Row 2, Column 2
• A water bottle in the third row and second column → That’s Row 1, Column 2
• A football is already drawn in the bottom left corner → That’s Row 1, Column 1

You keep following the clues until you reach the treasure!

Grid Game – Treasure Hunt

For Example: Let’s see how Jagat and Mini are playing.

Jagat thinks of a Mango.

Drone Around the School

Gyan brought a drone—a small flying camera—that can take pictures from above. He used it to take a top view of the school, and now his friends can see the whole school from the sky!

The drone helps us see:

• Buildings
• Playground
• Paths and parks
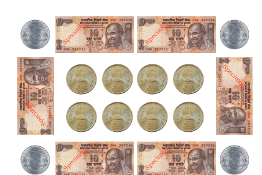
• Classrooms and school areas

This is called a top view—it’s like looking down at the school from the sky!

Try yourself:

What shape does a water bottle look like from the top?

• A.Circle
• B.Rectangle
• C.Triangle
• D.Square

View Solution

Exploring Paths and Directions

• A sight map provides a visual layout of a place, such as a school, showcasing various areas like classrooms, a stage, and a kitchen.
• On a map, we can trace different paths to navigate from one location to another, like going from the Grade 4 classroom to the stage.
• These paths can differ in length, with some being shorter and more direct than others.
• Directions are given using terms like left, right, up, or down to help someone find their way. For example, to get to the mid-day meal kitchen from the entrance, you would turn left and follow the designated path.

It’s important to note that in grid games or maps, diagonal movements are not permitted.

Example 2: Fill in the table below by writing the correct top view and side view for each object:

Ans:

Introduction

In this chapter, we will explore the exciting world of shapes that surround us in buildings, objects, and even nature. From your pencil box to the tallest towers—everything is made up of different shapes. But have you ever thought about what makes a cube different from a cylinder, or how a circle is made?

Let’s build with Diksha!

Diksha visited famous monuments in Delhi, like:

• India Gate
• Qutub Minar
• Akshardham
• Jantar Mantar
  …and many more!

She saw how big and beautiful these buildings were.

Now she wants to build a small model of India Gate using her wooden blocks.

What Is a Model?

A model is a small copy of something big — like a mini version of a real building!

You can use shapes like cubes, cylinders, and rectangles to make a building model with blocks.

Let’s Build a Model Using Blocks!

India Gate is made using blocks

1. What parts are in your model?
Ans: The model has a roof made of blue and orange blocks, two pillars or walls on the sides, and a base made with green blocks.

2. Why did you choose those parts?
Ans: Because the real India Gate also has a big top part like a roof, two tall pillars or sides, and a strong base to stand on.

3. What shapes can you use?
Ans: You can use cubes and rectangles for the roof and walls, and square blocks for the base. This model does not use curved shapes like the real India Gate.

4. How is your model similar to the real building?
Ans: The model has a large top section like the India Gate, an open space in the middle like the archway, and pillar-like blocks on the sides.

5. How is it different from the real building?
Ans: The model is made of colorful plastic blocks instead of stone. It doesn’t have any carvings or small details. It also looks more like a simple house than an actual arch.

Q: What is common in all these bricks?
A: They are all solid and mostly shaped like rectangular blocks. They are strong and used to build things.

Understanding Shapes

We are going to learn following things in this chapter which are as follows:

Shapes are figures or objects that have a specific form or outline. They can be flat (2D) or have volume (3D). Shapes are everywhere around us and help us describe the world.

Look around your classroom or home — can you name some objects that have shapes?

Ans: Yes! A clock (circle), a notebook (rectangle), a dice (cube), and a ball (sphere).

1. 2D Shapes (Two-Dimensional)

These are flat shapes with only two dimensions – length and width. 

Examples of 2D Shapes:

Examples of 2-D Shapes

1. Circle

• Round shape with no corners or edges.
• Example: A coin.

2. Square

• Four equal sides and four right angles.
• Example: A chessboard square.

3. Rectangle

• Opposite sides are equal, with four right angles.
• Example: A book cover.

4. Triangle

• Three sides and three corners.
• Example: A slice of pizza.

2. 3D Shapes (Three-Dimensional)

These shapes have three dimensions – length, width, and height. 

Examples of 3D Shapes:

• 1. Cube:
  • All sides are squares.
  • It has 6 faces, 12 edges, and 8 corners (vertices).
  • Example: Rubik’s cube.
• 2. Sphere:
  • No edges or corners.
  • It’s perfectly round in all directions.
  • Example: Soccer ball.
• 3. Cylinder:
  • Two identical flat circular ends and one curved side.
  • It has 2 edges and no corners.
  • Example:  Soup can.
• 4. Cone:
  • One circular base and a single vertex (point).
  • It has 1 edge.
  • Example: Party hat.
• 5. Rectangular Prism (Cuboid):
  • Faces are rectangles.
  • It has 6 faces, 12 edges, and 8 vertices.
  • Example: brick.

Try yourself:

What type of shapes are flat and have only length and width?

• A.3D Shapes
• B.2D Shapes
• C.Geometric Shapes
• D.Angles

View Solution

Sorting 3D Shapes

3D shapes, unlike 2D shapes, have depth in addition to height and width. This extra dimension gives 3D shapes their unique properties and allows them to occupy space. 
Let’s delve into the different types of 3D shapes and their characteristics.

1. Cube

• A cube is a 3D shape that has 6 faces, all of which are squares.
• It has 8 corners (also known as vertices) where the edges meet.
• A cube also has 12 edges, which are the lines where two faces meet.

Some examples of a Cube shape are:

2. Cuboid

• A cuboid is similar to a cube but has 6 faces that are rectangles.
• It also has 8 corners and 12 edges, just like a cube.
• A cuboid is also known as a rectangular prism.

Some examples of Cuboid are: 

3. Triangular Prism

• A triangular prism has 5 faces, 2 of which are triangles and 3 are rectangles.
• It has 6 corners and 9 edges.

Some examples of Triangular Prism are: 

4. Square Pyramid

• A square pyramid has 5 faces, with 1 square base and 4 triangular faces.
• It has 5 corners and 8 edges.

Some examples of Square Pyramid are:

5. Triangular Pyramid

• A triangular pyramid, also known as a tetrahedron, has 4 triangular faces.
• It has 4 corners and 6 edges.

Some examples of Triangular Prism are:

Try yourself:

What shape has 6 faces that are all squares?

• A.Cube
• B.Cuboid
• C.Triangular Prism
• D.Square Pyramid

View Solution

6. Sphere

• A sphere has 1 curved face and no edges or corners.

Some examples of Sphere are:

7. Cylinder

• A cylinder has 2 flat circular faces, 1 curved face, and 2 edges where the curved face meets the circular faces.

Some examples of Cylinder are: 

8. Cone

• A cone has 1 flat circular face, 1 curved face, and 1 edge where the curved face meets the circular face.

Some examples of Cone are: 

What’s the difference between a prism and a pyramid?

• A prism has two same-shaped flat faces (top and bottom).
• A pyramid has only one flat base, and all sides are triangles that meet at a point.

Parts of 3D Shapes

• 1.  Face
  • A face is a flat surface on a 3D shape.
  • In the image, the square labeled “face” is one of the cube’s flat sides.
• 2. Edge
  • An edge is the line where two faces meet.
  • In the image, the arrow labeled “edge” points to one such line between two faces.
• 3. Vertex and Vertices
  • A vertex is a point where three edges meet. It is also known as a corner.
  • The green dots in the image show the vertices.
  • When there is more than one corner, we use the word vertices.

As you can observe, the faces of a cube and cuboid are flat, whereas a cylinder, cone and sphere have curved faces.

Now, let us find out how many faces, edges and corners does each shape have. For a cube and cuboid, pick up a die and a geometry box and count the number of faces, edges and corners. You will notice that both the cube and cuboid have 6 faces, 12 edges and 8 corners. 

Now, from the figure given above, try to count the same for cone, cylinder and sphere.  You will find that: A cylinder has 3 faces (2 flat, 1 curved), 2 edges and 0 corners.  A cone has 2 faces (1 flat, 1 curved), 1 edge and 1 corner.  A sphere has only 1 curved surface.

Euler’s Formula. This formula describes the relationship between the number of faces (F), corners (V), and edges (E) in many 3D shapes. For convex polyhedra, the formula is F + V – E = 2. This mathematical relationship helps in understanding the properties of 3D shapes.

Try yourself:

How many edges does a cylinder have?

• A.2
• B.3
• C.0
• D.1

View Solution

Nets of 3D Shapes

A net is a two-dimensional layout that can be folded to form a three-dimensional shape. It shows how the surfaces of a 3D object are connected.

Example. The net of a cube consists of 6 squares, which when folded along the edges, form the faces of the cube. Similarly, the net of a cuboid is made up of 6 rectangles that fold to create the rectangular faces of the cuboid.

Take a die or any other cube and trace all its faces on a sheet of paper. What is the shape of all the six faces?
They are all squares of the same size. Thus, you see that a cube can be made from six squares joined together in a particular manner.

We have many more nets (arrangements of these squares) that can be folded up to form a cube.
We can also form nets with 5 square faces. In this case it will be a box with no lid.

When Lines Meet

An angle is made when two lines meet at a point. This point is called the corner or vertex.

 Angles are found in every shape we see — from the chair you sit in the house to the corner of your book!

• Right Angle: An angle that measures 90 degrees, resembling the corner of a square.

• Acute Angle: An angle smaller than a right angle.

• Obtuse Angle: An angle larger than a right angle.

Shapes with Straws

• Triangles: Shapes with three sides that can have acute, right, or obtuse angles.

Similarly you can try with Rectangular shape.

Q: What result we will get?

Ans: All corners in a rectangle are right angles.

Let’s Summarise:

Try yourself:

What shape do all six faces of a cube have?

• A.Squares
• B.Rectangles
• C.Pentagons
• D.Triangles

View Solution

Sorting Shapes

By Faces: A face is the flat surface of a 3D shape. Just like how a dice has 6 flat sides, each flat side is called a face.

By Edges: An edge is where two faces meet. It’s like the corner of a box or the side of a triangle.

By Angles: An angle is where two lines or edges meet. Angles are found in flat (2D) shapes like triangles and rectangles.

Some Solved Examples 

Q1: Mira sees a coin, a book, and a pizza slice. What shape is each one?

Ans: 

A coin is a circle(round with no corners).

A book is a rectangle (opposite sides equal).

A pizza slice is a triangle (3 sides and 3 corners).

Q2: Which of these shapes has a curved surface: cube, cone, or sphere?

Ans: Cone and sphere have curved surfaces. A cube has only flat faces.

Q3: A cuboid has 6 faces, 8 corners, and 12 edges. Does it follow the rule: Faces + Vertices – Edges = 2?

Ans: 6 + 8 – 12 = 2
Yes, it follows Euler’s Formula.