Chapter Notes: Fun with Numbers

What are Numbers?

A number is a value we use for counting and calculating. Numbers can be shown in different ways: as words (one, two, three) or as figures (1, 2, 3). We can also group numbers by how many digits they have.

• Single-digit numbers have only one digit, for example 1, 2, 3, 4.
• Two-digit numbers have two digits, for example 10, 25, 99.
• Three-digit numbers have three digits, for example 100, 345, 897.

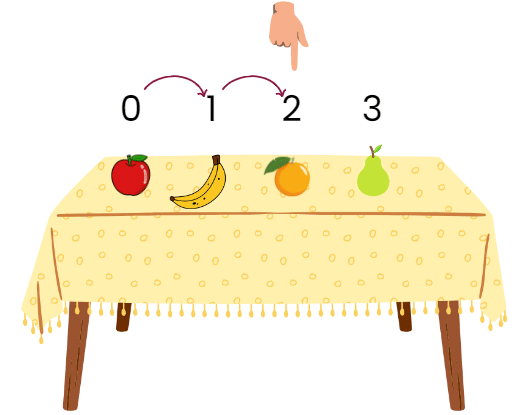
Now, students, can you count how many flowers there are?

By counting these, we can see that there are a total 36 flowers.

Step Counting

Let us now read an interesting story!.

Once upon a time, there was a little kangaroo named Skip who loved counting. Regular counting was slow for Skip, so he invented step counting.

Instead of going one by one, he jumped ahead or backwards by a fixed number each time. His friends liked it and soon everyone in the jungle was step counting, making counting fun and fast!

What is Step Counting?

• Step counting means counting numbers by adding the same amount each time. For example, if you add 2 each time, you count 0, 2, 4, 6, 8, …
• Backward skip counting is counting in reverse. Instead of going forward, you start from a larger number and subtract a certain amount each time to reach the next number. It’s just like walking backwards but with numbers. For example, counting backwards by 3 from 10 gives 10, 7, 4, 1.
• Step counting helps you see number patterns and makes counting faster and more fun.

Forward Step Counting

In forward step counting we start at a number and keep adding the same amount to get the next number.

Skip count by 2

• Start at 0 and add 2 each time.
• 0 + 2 = 2
• 2 + 2 = 4
• 4 + 2 = 6
• 6 + 2 = 8
• Continue this process: 10, 12 and so on until 12 or further.

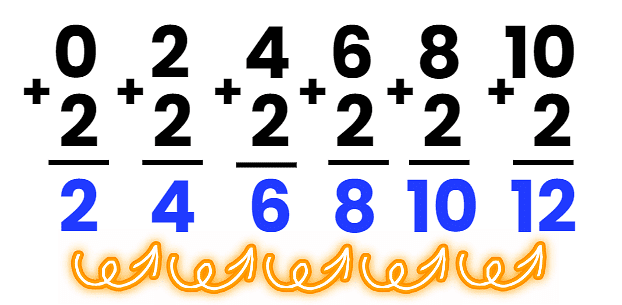
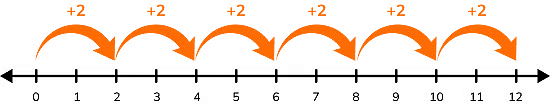
• You can skip count starting at any number. For example, skip count by 2 starting at 5 gives:

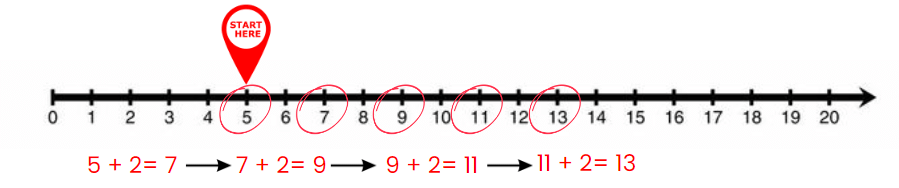
• 5, 7, 9, 11, 13 …

Skip count by 5

• In skip counting by 5, we add 5 each time and move forward.
• If Skip the kangaroo starts from 5 and skips by 5, the numbers he reaches are:

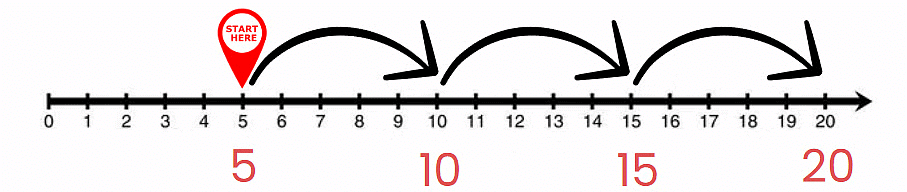
• 5 + 5 = 10
• 10 + 5 = 15
• 15 + 5 = 20
• So the series is 5, 10, 15, 20, …

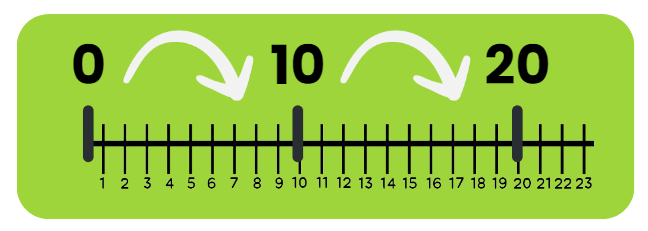
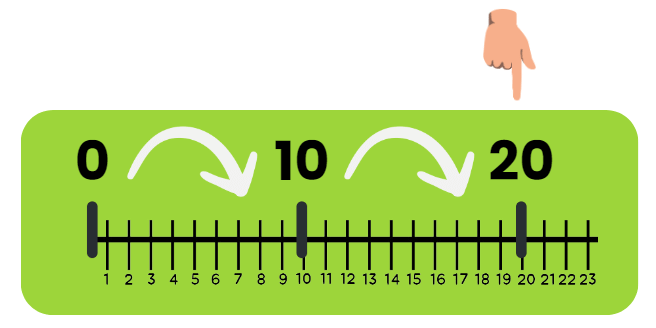
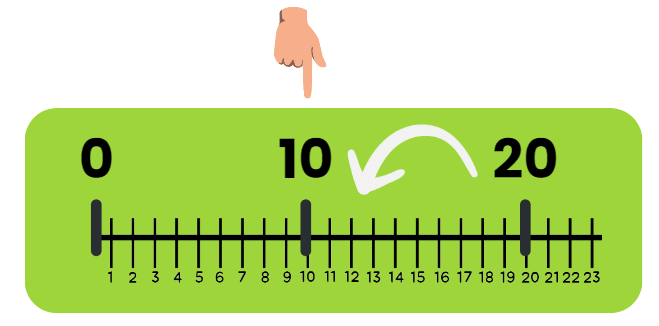
Skip count by 10

• Look at the picture of the kangaroo jumping. Complete the pattern by finding how much it jumps each time.

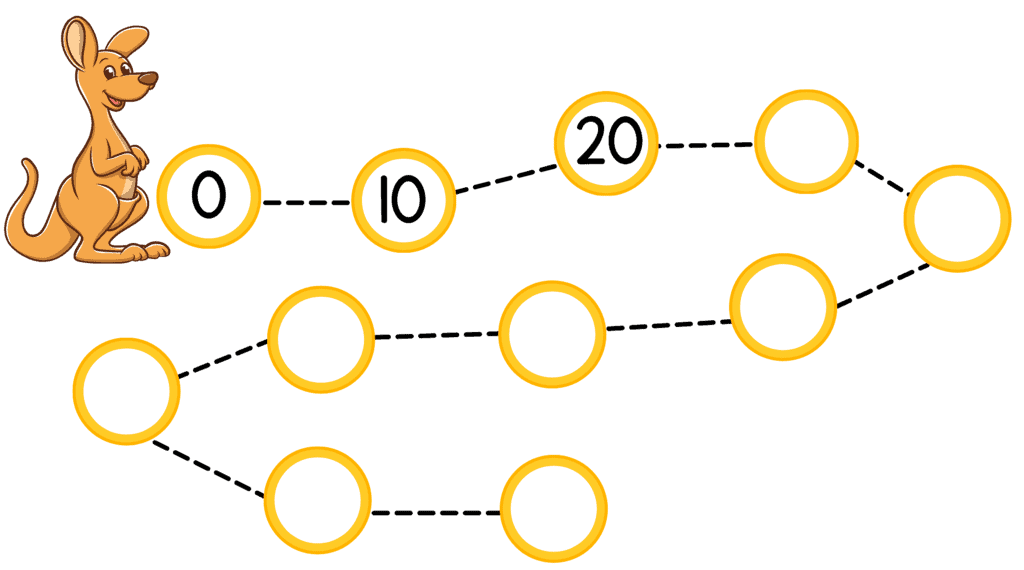
• We can see that the kangaroo first jumps from 0 to 10, then from 10 to 20.
• We can use subtraction to find the jump size: 20 – 10 = 10.
• Also 10 – 0 = 10, so the difference is 10.
• Thus, to continue the series we add 10 each time.

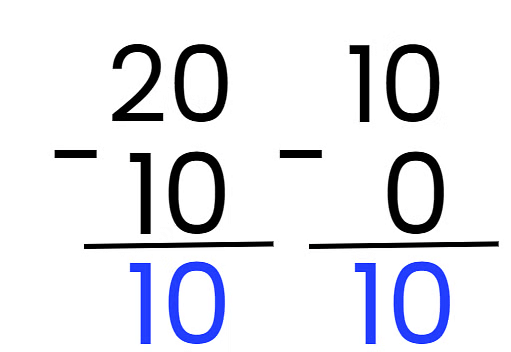
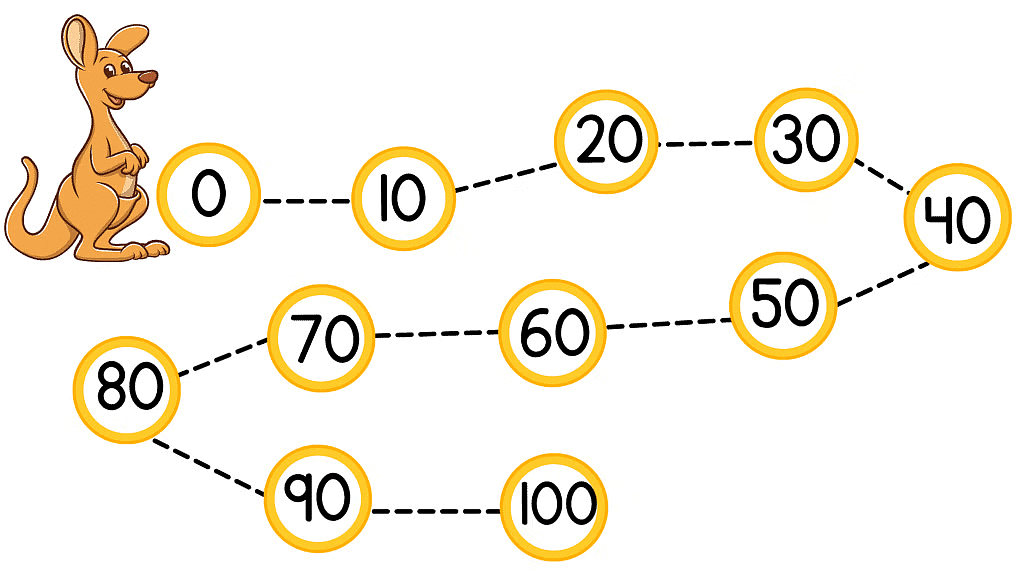
• The complete series is: 0, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100.

Backward Skip Counting

• What we have learned so far is called forward skip counting, which implies we are counting in the forward direction and adding a certain number to each previous number to obtain the next number in the series. 
• Now, we will discuss backward skip counting. 
• Backwards skip counting is a way of counting numbers in reverse order by skipping a certain amount each time. Instead of starting from a lower number and counting up, you start from a higher number and count down. For example, if you’re skip counting backward by 3s from 10, it would go like this: 10, 7, 4, 1. 

Backwards skip count by 3

• Start with a number and subtract 3 each time.
• Starting from 100:

100 – 3 = 97

97 – 3 = 94

94 – 3 = 91

91 – 3 = 88

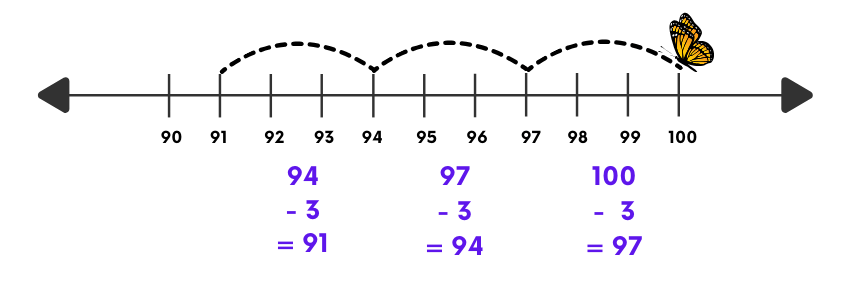
• The series is: 100, 97, 94, 91, 88, … These numbers are in descending order.

Backwards skip count by 20

• Let’s imagine we’re on a backwards adventure, counting by 20s. Instead of walking forward, we’re taking big jumps backwards.
• Start at 100 and subtract 20 each time:

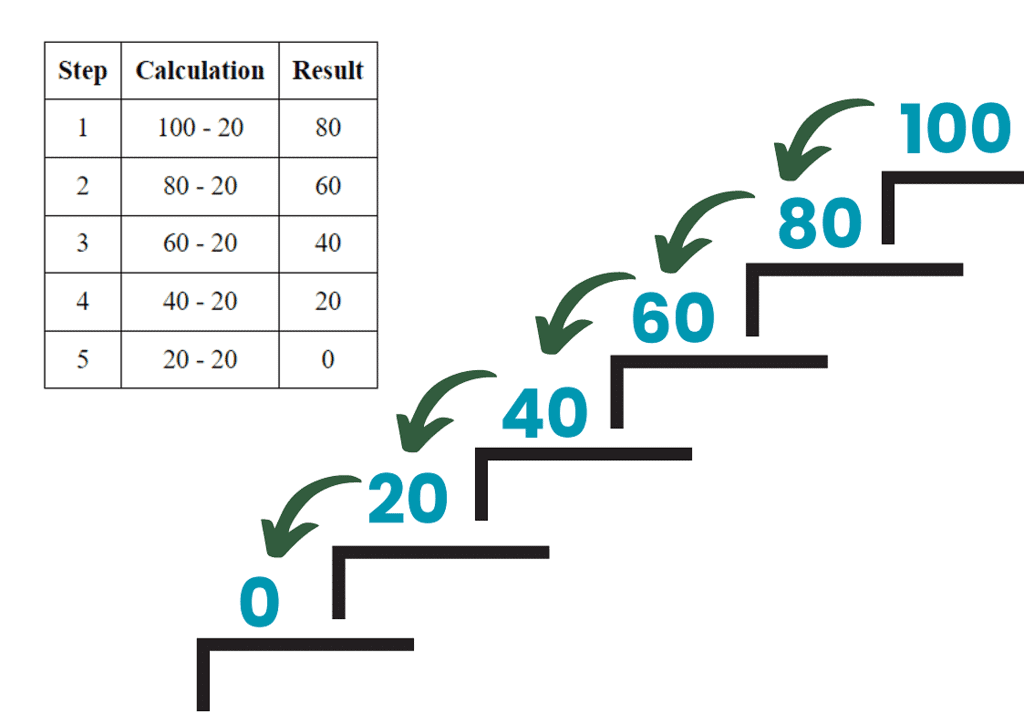
100 (start)

80 (100 – 20) – we took one step back, like a giant leap!

60 (80 – 20) – another big step backward

40 (60 – 20) – we’re really moving now!

20 (40 – 20) – almost there!

0 (20 – 20) – and we’ve reached the end of our backward journey!

Guess My Place

• Now, let us play a game in which we guess where the ants are sitting on a number line.

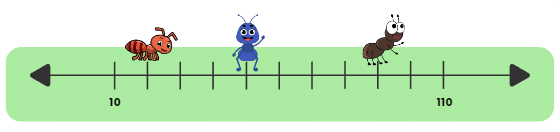
• Look at the number line, and answer the following questions:

(a) Which number is the red ant sitting on?
(b) Which number is the blue ant sitting on?
(c) Which number is Brown Ant sitting on?

• First fill the number line from 10 to 110 with equal gaps of 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110.

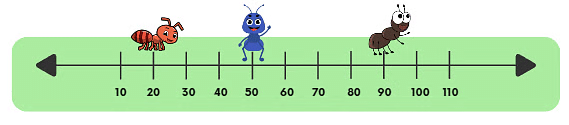
• Answers:
  (a) Red ant is sitting at number 20.
  (b) Blue ant is sitting at 50.
  (c) Brown ant is sitting on number 90.

Exploring Patterns

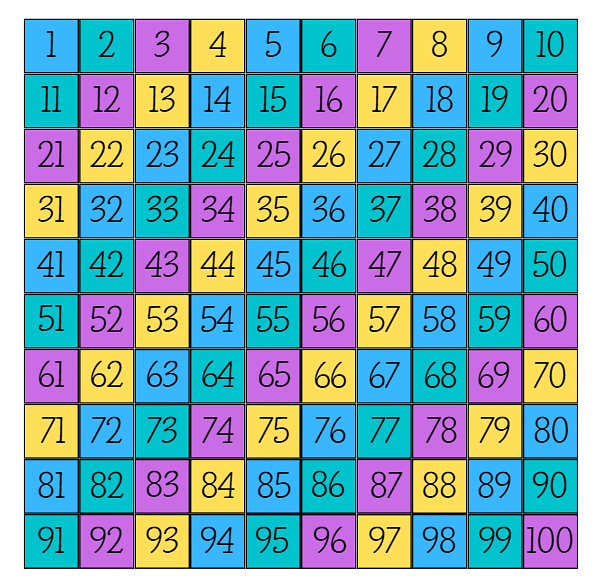
Q: Look at the number chart and write down the answers.

__9___ comes just before 10
__19___ comes just before 20
__29___ comes just before 30
__39___ comes just before 40

Q: What is the pattern here?

Ans: Let us subtract to see the difference.
19 – 9 = 10
29 – 19 = 10
39 – 29 = 10
We can clearly see that the difference is 10.
The pattern continues: 9, 19, 29, 39, 49, 59, …

Q: Now, look at the numbers coloured purple in the number chart. Write them.

7, 16, 25, ____, ____, ____, ____, ____, ____, ____

Ans: 7, 16, 25, 34, 43, 52, 61.

Q: What is the pattern?

Ans: The difference is 9. Nine has been added to each number.

Look at this fun number window

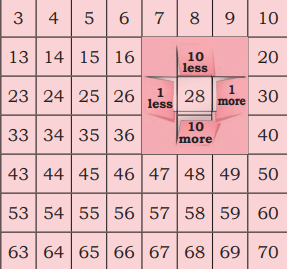
Using the number window, we can find numbers above, below, left and right of a given number by adding or subtracting 1 or 10.

Fill in the blocks given below:

Observe how blocks are placed and extend the pattern further.

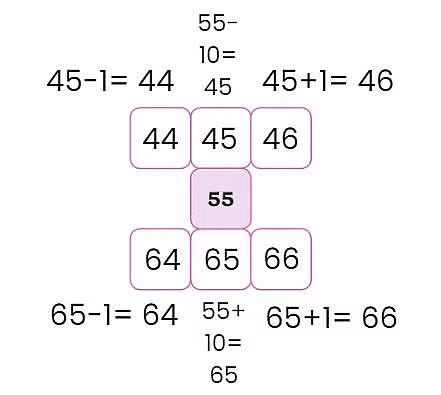
To find the block above 55, subtract 10: 55 – 10 = 45.

To find the block below 55, add 10: 55 + 10 = 65.

Now, moving on to the above row, we have found the middle block, which is 45. To find out the block on its left, we need to subtract 1 from it.
45-1 = 44
To find out the number on its right, we need to add 1 to 45 which gives us 46.
Similarly, we find out the numbers in the last row.

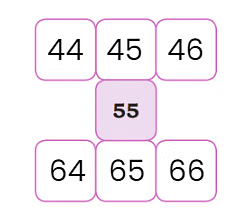
Let’s look at some more examples of number grids:

1.

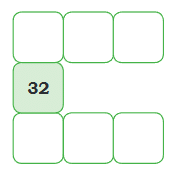
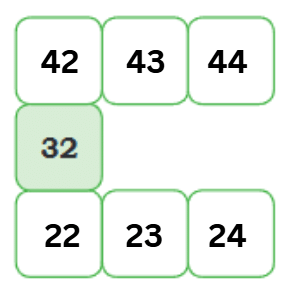
Using the same logic, add numbers to this grid:

2.

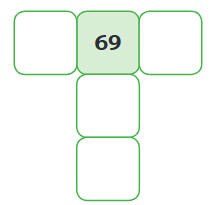
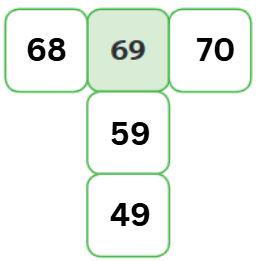
Let’s fill up this magic grid:

Hope you enjoyed playing with numbers and exploring different games. Keep practising and having fun!

Story Time: Kunal’s Bakery

Hey kids! Let’s learn why organising information is important?

• Once upon a time, in a town filled with sweet smells and delicious treats, there was a bakery owned by a kind man named Kunal. 
• He had so many different types of cakes and desserts in his shop, from chocolate cakes to strawberry tarts.

• One sunny day, a customer named Hardik visited Kunal’s bakery. 
• Hardik wanted to buy all the yummy desserts, but he needed to know how many of each type were available. 
• Kunal tried to count, but it was a bit tricky. 

• That’s when Kunal called his smart friend Navroop for help.
• Navroop had a clever idea. She took out a piece of paper and made a table with the names of all the desserts. 
• Then, together with Kunal, they counted how many of each dessert they had and filled in the table. 

• For example, if there were 1 strawberry cake, they wrote ‘1’ in the column next to ‘Strawberry Cake.’

• This table helped them organize all the data and also made it easy to create the final bill for Hardik. 
• And that’s how Kunal and Navroop learned the importance of organizing data, which is what data handling is all about!

Data handling is about organizing information systematically, like arranging books on a shelf by genre, making it easier to understand and use through tables, charts, and graphs.

What is Data?

• Data is like pieces of information, such as numbers, words, or observations, that we collect and use to learn things or make decisions. 
• It is very important and useful to organise data. there are several ways to organise data. 

Let’s now understand different ways of organising data.

Tables

• Tables are like organized lists with rows and columns where we can write down information neatly.
• They help us keep track of things and compare different pieces of information easily. 
• In the above story, Kunal and Navroop used a table to organise their data.

Table made by Kunal & Navroop

Let’s now Practice making a table with Shankar.

Learn by Practicing: Shankar’s Button Collection Adventure- 1

Once upon a time, there was a curious boy named Shankar who loved collecting buttons of different colors and sizes. 

• One fine day, as he sat admiring his collection, he decided it was time to organize them properly.

Step 1: Shankar took out a piece of paper and drew a table with columns for colors and rows for types of buttons.

Step 2: He carefully listed down all the colours of buttons he had, like blue, yellow, red, and green.

Table Made by Shankar

Step 3: Shankar then started counting each type of button. He counted:

• 4 blue buttons
• 3 yellow buttons
• 5 red buttons
• 2 green buttons
  Table filled by Shankar

Excitedly, he filled in the table with the number of buttons for each colour.

By organizing his button collection on a table, Shankar could easily see how many buttons he had of each colour, making it fun and simple to manage his treasured collection!

Now that we know how tables help us, Let’s move on to charts.

Charts

Charts are like colourful pictures that show information in a fun way, like how many friends like different colours. They help us see patterns and understand numbers easily, like counting how many red, blue, or green buttons we have in a collection.

Learn by Practicing: Shankar’s Button Collection Adventure- 2When Shankar showed his table to his friend Richa, she smiled and said, “Tables are great, but charts are even more fun! Let’s turn your button collection into a colourful chart!”

Richa & Shankar

• Excited by Richa’s idea, Shankar took out a big piece of paper and drew a beautiful chart with colourful columns for each type of button colour: blue, yellow, red, and green. 

• He counted the buttons again and placed colourful stickers on the chart to represent each colour.

• As Shankar stepped back to admire his button chart, he realized that Richa was right. 
• The chart made it so easy to see which colour had the most buttons and which had the least. 
• It was like turning his collection into a colourful work of art that also helped him understand his buttons better! 

Isn’t it amazing how organizing information can make things so much easier? Just like Kunal and Navroop organized their dessert data in a table and Shankar used both tables and charts to organize his button collection, we can also organize information to understand it better.

Remember, data can be like a puzzle, and tables and charts are like tools that help us solve that puzzle and see the bigger picture. So, the next time you have a lot of information to manage, think about how you can use tables and charts to make it simpler and more fun! Happy organizing!

Money 

• Hey kids! You have seen money, right? 
• We use money daily. you must have seen your parents giving money when you go to market to buy your favourite fruit, or toys. 
• Money is like special coins and colourful paper that we use to buy things we want, like toys, books, or ice cream. 
• It helps us trade for stuff we like! 

Now, let’s hear what Dadaji has to say about money!

Dadaji & money

Once upon a time, in a village, there lived a kind and wise grandfather called Dadaji. One sunny afternoon, Dadaji gathered all the children under a big, shady tree and began to share something fascinating—money!

“Children,” Dadaji said with a warm smile, “did you know that in our country, money comes in various forms? 

• We have special coins and colorful notes that we use to buy things.”
• He showed the children a shiny one-rupee coin, a slightly bigger two-rupee coin, and a round five-rupee coin.

Different coins

• “These are some of the coins we use,” Dadaji explained. 
• “They have different values, but they all help us buy things we need.”
  
• Dadaji then displayed a one-rupee note, a two-rupee note, and a five-rupee note.
•  “And these are our rupee notes,” he said. “We also have coins for 10 rupees, 20 rupees, and even a 50-rupee note!”

• Dadaji further told them that there are even bigger notes, means that notes that have higher value. For example 500 Rupee note.

500 Rupee note

• The children were fascinated as Dadaji talked about the different types of coins and notes in India. 
• They learned that coins and notes are like little helpers that we use every day to buy food, toys, books, and other things we need.
• Dadaji concluded the story by saying, “So, my dear children, next time you see a coin or a note, remember how special they are. They help us trade and buy things, making our lives easier and more colorful!”

Now that we know about different types of notes, let’s help Jaspreet.

Adding Money: Let’s help Jaspreet

Once upon a time, there was a girl named Jaspreet who had been saving up in her wallet to buy a beautiful doll she had her eyes on. The doll cost 200 rupees, and Jaspreet was excited to see if she had enough money in her wallet to buy it.

Jaspreet with her wallet

Jaspreet’s wallet was filled with a variety of notes and coins. She had:

• One 100-rupee note
• Two 50-rupee notes
• Three 20-rupee notes
• Four 10-rupee notes
• Five 5-rupee coins
• Six 1-rupee coins.

Let’s help Jaspreet by counting the money in her wallet to see if she has enough to buy the doll. We add up the values of each note and coin:

After carefully counting, we find that Jaspreet has:

• 100 rupees (from the 100-rupee note) + 100 rupees (from the two 50-rupee notes) + 60 rupees (from the three 20-rupee notes) + 40 rupees (from the four 10-rupee notes) + 25 rupees (from the five 5-rupee coins) + 6 rupees (from the six 1-rupee coins) = 331 rupees

That means Jaspreet has more than enough money to buy the doll she wants and even have some left over! Jaspreet is overjoyed !

We learn an important lesson about the value of money and how adding up the values of different notes and coins can help us determine if we have enough money to buy what we want.

Story Time: Adventure of different Seasons

Hey kids! Today we will learn about different seasons with Aashi & Rahul. Let’s begin the story!

• Once upon a time, there was a girl named Aashi who loved looking out of her window. 
• One day, she noticed something strange. 
• There was fluffy white snow covering everything outside! 

• She remembered that just a few months ago, on her birthday in August, it was sunny and very hot. Aashi felt confused and decided to go to her brother Rahul for an explanation.
• When Aashi asked Rahul about the sudden change in weather, Rahul smiled and said, “Aashi, there are five seasons in a year, and they keep changing to make our world interesting.”

Rahul explained each season to Aashi using simple words:

• Spring: This season begins with cheer! Flowers bloom everywhere, and birds sing happily in the trees.
  Spring
• Summer: It’s the season of heat and sunshine. People enjoy their vacations, and festivals like Gudi Padwa, Shivratri, and Baisakhi are celebrated with joy.

Summer

• Monsoon/Rainy Season: During this time, rainfalls bring joy to everyone. People celebrate festivals like Janmashtami and Raksha Bandhan, enjoying the coolness after the rain.

Monsoon

• Autumn/Fall: As autumn arrives, leaves start falling from trees, and the winds become pleasantly cool. Festivals like Dussehra and Sharad Purnima are celebrated with enthusiasm.

Autumn

• Winter: When winter comes, the air gets cold, and sometimes we even see snow! Festivals like Christmas and Lohri are celebrated during this cozy season.
  Winter

Aashi nodded, understanding that each season brings its own magic and beauty to the world. She learned that these seasons cycle through the months, making life interesting and full of surprises.

Calendar

A calendar is like a special chart that tells us the days, months, and helps us plan our time better. It looks like this: 

Days in Months

When we count days, we start at 1 and keep counting until we reach the end of the month.

• Months like January, March, May, July, August, October, and December, we count up to 31 because these months have 31 days. They’re like the longer months of the year.

• But for some other months, like February, April, June, September, and November, we count up to only 30 days because these months have 30 days. 

• February is a bit special because sometimes it has 28 days and sometimes 29 days, depending on the year. 
• That’s because every four years, we add an extra day to February to keep our calendar accurate. We call that year a leap year!

So, some months have 30 days and others have 31 days because of how the Earth moves around the sun, and February is special because it can have either 28 or 29 days.

How Long Does it Take?

Different things take different amout of time to occus. So there are different measurements of time. Let’s see Sagar’s adventure to understand better.

Story Time: Sagar’s Questions

• Once upon a time, there was a curious boy named Sagar. 
• He loved to ask questions about everything around him. 
• One day, while doing his homework, Sagar wondered, “How long does it take to finish my homework?“

• He asked his mom, who said, “It usually takes you about 1 hour to finish your homework.” 
• Sagar was amazed that time could be measured in hours.
• As days went by, Sagar noticed something interesting in his garden.
   
• He saw a tiny seed growing into a beautiful flower. He wondered, “How long does it take for a flower to grow?”
• He asked his grandma, who told him, “It takes a few days for the seed to sprout, then a few weeks for the plant to grow leaves and stems, and finally, after a few months, you’ll see a lovely flower bloom!” Sagar learned that growing a flower takes time, from days to months.
  
• One evening, while stargazing with his dad, Sagar asked, “How long does it take for the Earth to go around the sun?” 
• His dad smiled and said, “It takes about 365 days for the Earth to complete one orbit around the sun, and we call that one year.“
  
• Sagar was amazed at how we measure time in years.

As Sagar grew older, he learned more about time. He learned that:

• Hours are for short tasks
• Days are for events like birthdays and vacations
• Months are for changes like seasons
• Years are for big milestones like growing up and celebrating New Year.
  

Sagar realized that time helps us understand how long it takes to do things, from finishing homework to watching flowers grow and celebrating special moments in life.

Clock and Hours

Imagine a clock as a special tool that helps us see the hours in a day.

• A clock has numbers from 1 to 12 in a circle, and it also has two hands: a short hand and a long hand. 
• The short hand points to the hour, while the long hand points to the minutes.

Now, let’s talk about why there are 24 hours in a day. 

• A day is divided into two parts: daytime and nighttime.
  Day & Night
• During daytime, we have 12 hours from morning until evening, and during nighttime, we have another 12 hours from evening until morning. 
• When we add these two parts together, we get a total of 24 hours in a day.

How to see Time?

To see the time on a clock, you need to look at where the hands are pointing. The short hand tells us the hour, and the long hand tells us the minutes. 

• For example, if the short hand is pointing to the number 8 and the long hand is pointing to the number 12, it means it’s 8 o’clock.

Here’s a simple breakdown:

• When the short hand is on 1 and the long hand is on 12, it’s 1 o’clock.
  1 o’clock
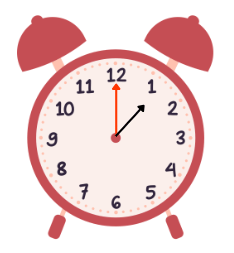• When the short hand is on 2 and the long hand is on 12, it’s 2 o’clock.
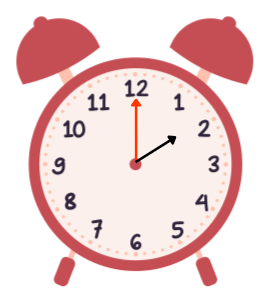  2 o’clock
• And so on, until we reach 12 o’clock when the short hand is on 12 and the long hand is on 12 again.

You can practice reading the time on a clock by looking at where the hands are pointing and understanding that each number on the clock represents an hour, making a full cycle of 12 hours before starting again.

Knowing Directions

Directions are like instructions that tell us which way to go or which way something is facing. We need them to find our way around places, like finding the way home or to school. There are four main directions: north, south, east, and west.
Directions

• North is where the North Pole is
• South is where the South Pole is
• East is where the sun rises
• West is where the sun sets. 

Knowing these directions helps us understand where things are and how to get to different places.

Story Time: Vanya’s Introduction to Directions

• Once upon a time, Vanya was on a car journey with her mom and dad. 
• They were going to visit her grandparents who lived in a nearby town. 
• As they drove along the road, Vanya noticed her mom saying things like “turn right” or “go left” to her dad.
  
• Vanya was curious and asked her mom, “Why do you keep saying ‘turn right’ and ‘go left’ to Dad?”
• Her mom smiled and explained, “These are called directions, Vanya. Directions help us know which way to go when we are driving or walking. There are four main directions: north, south, east, and west.”
• Vanya’s eyes widened with interest. “North, south, east, and west? How do we know which one is which?“
  
• “Well,” her mom continued, “imagine you are standing in the middle of a big circle. If you face the rising sun in the morning, that’s east. If you turn towards where the sun sets in the evening, that’s west. North is in front of you, and south is behind you.”
  
• Vanya nodded, trying to picture it in her mind. “So, when you say ‘turn right,’ Dad goes towards the east or the west?“
• “Exactly!” her mom replied. “When I say ‘turn right,’ Dad goes towards the right side of the road, which could be east or west, depending on which direction we are driving.”
• Her mom nodded, “Exactly! ‘Right’ means towards the houses, and ‘left’ means towards the trees.”
  Left & Right
• Vanya tried to remember. “So, if I want to go to the park, I should go left from our house?”
• “Yes, you got it!” her mom exclaimed. “And if you want to go to the store, you should turn right from our house.”

Vanya felt proud of herself for understanding. From then on, whenever they drove or walked, Vanya would confidently say, “Turn right here!” or “Let’s go left at the next corner!”  

Through these stories, we’ve unlocked the secrets of seasons, time, calendars, clocks, and directions. Isn’t it fascinating how much we can learn from the world around us? Keep exploring and asking questions, just like Aashi, Rahul, Sagar, and Vanya did, and you’ll discover even more wonders! Good Job!

Story Time: Grouping

Hey kids! Let’s learn a math trick from Rahul.

• One sunny day, Rahul and Disha were playing in the garden. 
• Disha spotted colorful butterflies fluttering near the flowers.
  
• She got excited and started counting, “1, 2, 3, 4…” Rahul, curious about what Disha was doing, asked her.
• Disha explained, “I’m counting the total number of wings all the butterflies have.”

• But as Disha counted, she realized it was tricky because the butterflies kept moving. 
• Seeing her struggle, Rahul came up with a clever idea. 
• He said, “Disha, I have a trick that will help you find the total number of wings quickly using math. Are you ready?”
• Disha nodded eagerly, curious to learn Rahul’s trick.

Step One: “First, tell me how many butterflies are there?” Rahul asked.

• Disha counted and replied, “There are 5 butterflies.“

Counting Butterflies

Step Two: Rahul observed that each butterfly has 2 wings. 

• He said, “Good! Now, remember that each butterfly has 2 wings.”

Step Three: Rahul explained to Disha, “If there are 5 butterflies and each butterfly has 2 wings, you can add 2, 5 times to know the total number of wings.

• “He showed her how to do it: 2 + 2 + 2 + 2 + 2 = 10 wings.
• Disha’s eyes lit up as she understood the trick. 

• “So, 5 times 2 is 10 wings!” she exclaimed happily.
• Rahul smiled and said, “Exactly! You can use this trick to quickly find the total number of wings when you know how many butterflies there are and how many wings each butterfly has.”

Just how Rahul and Disha solved the mistry of butterfly wings, we can use this tick to calculate so many other things. Let’s try to help Tanya using the same trick.

Learn by Practicing- 1

Tanya is a sweet girl and organising her things. She had different boxes of pencils and each box had multiple pencils. Let’s help Tanya in finding how many pencils she has. 

Step 1: Let’s count the number of boxes.

There are 6 boxes.
Counting Boxes

Step 2: Count the number of pencils in each box.

Each box has 8 pencils.

Counting pencils

Step 3: Now, let’s see how many pencils Tanya has in total:

• Total pencils = 8 + 8 + 8 + 8 + 8 + 8 = 48
• We are adding 8 for 6 times.
• So, 6 times 8 is also 48 or 6 groups of 8 give 48.
• Also, ‘times’ can be written as ‘x’. 
• So, 6 x 8 = 48.

MultiplicationAs you observed in our example, we used “times” and “x” above. In math, this concept is called multiplication. Let understand what this means:

• When we say “6 x 8,” we are using ‘x‘ as a way to show multiplication. It means we are taking 6 groups of 8 and adding them together to find the total.
• For example, imagine you have 6 groups of 8 pencils each. 
• To find out how many pencils you have in total, you can count them one by one, or you can use multiplication.

Sign of Multiplication

• So, when we write “6 x 8,” it’s like saying “6 groups of 8” or “8 pencils repeated 6 times.” We use ‘x’ to show this grouping or repetition.
• In simple terms, multiplication helps us quickly find out the total when we have the same number repeated several times. And in math, we write “times” as ‘x’ to represent this idea of groups or repetitions.
• So, “6 x 8” means you have 6 groups of 8 pencils each, which gives you a total of 48 pencils.

This is why we study tables. Let’s see what are Tables

Tables

They are sets of calculations that we study to make our calculations easy and quick. 

Let’s try to understand the table of 2.

Table of 2

The “table of 2” is a list of numbers that we get when we multiply 2 by other numbers, like 1, 2, 3, and so on, up to 10. It helps us quickly figure out the answers when we do multiplication with the number 2. 

When we say “2 ones are 2,” it means that if we have 2 groups, each with just 1 thing in it (like 2 groups of 1 cookie each), we have a total of 2 things. It’s like saying that when we count 1 thing twice (2 times), we get 2. 

We have a “table” for each number, just like we have a table of 2. This table helps us quickly find out the answers when we do multiplication with that number. Here are the tables for 3, 4, 5, and 10:

Table of 3

Just like Table of 2, we have table of 3, Let’s see how it looks like:

This table is read like : 

• 3 ones are 3
• 3 twos are 6
• 3 threes are 9
• 3 fours are 12
• 3 fives are 15
• 3 sixes are 18
• 3 sevens are 21
• 3 eights are 24
• 3 nines are 27
• 3 tens are 30

Table of 4

This table is read like :

• 4 ones are 4
• 4 twos are 8
• 4 threes are 12
• 4 fours are 16
• 4 fives are 20
• 4 sixes are 24
• 4 sevens are 28
• 4 eights are 32
• 4 nines are 36
• 4 tens are 40

Table of 5

This table is read like :

• 5 ones are 5
• 5 twos are 10
• 5 threes are 15
• 5 fours are 20
• 5 fives are 25
• 5 sixes are 30
• 5 sevens are 35
• 5 eights are 40
• 5 nines are 45
• 5 tens are 50

Table of 10

This table is read like :

• 10 ones are 10
• 10 twos are 20
• 10 threes are 30
• 10 fours are 40
• 10 fives are 50
• 10 sixes are 60
• 10 sevens are 70
• 10 eights are 80
• 10 nines are 90
• 10 tens are 100

Story Time: Magic of Multiplication

• Once upon a time, there were three friends named Sam, Lily, and Max. 
• They loved playing with marbles in their backyard. 

Sam, Lily & Max

• One sunny day, they decided to arrange their marbles in rows to count them easily.
• Sam put 4 marbles in each row, making 3 rows in total. 

3 rows of 4 marbels in each row

• Lily, being curious, asked Sam, “How many marbles are there in all three rows?” Sam replied, “Let’s count them together.” 
• They counted each marble in the rows and found out there were 12 marbles in total.

• Excited by this, Max wanted to try something different. 
• He arranged his marbles in columns instead of rows. 
• He put 3 marbles in each column and made 4 columns. 

• Lily asked Max, “How many marbles are there in all four columns?” Max smiled and said, “Let’s count them like we did before.” 
• They counted each marble in the columns and were surprised to find out that there were also 12 marbles in total!
• Sam, Lily, and Max were amazed and realized that no matter how they arranged the marbles, whether in rows or columns, the total number of marbles remained the same at 12. 

They learned that 3 times 4 is 12, just like 4 times 3 is also 12, because multiplication is about grouping things together in different ways but getting the same total amount in the end.

Making Table from Tables

Did you know that we can create new tables by adding the values from two existing multiplication tables? Let’s take an example with the tables of 2 and 3.

Table of 2:

• 2 ones are 2
• 2 twos are 4
• 2 threes are 6
• 2 fours are 8
• 2 fives are 10 …

Table of 3:

• 3 ones are 3
• 3 twos are 6
• 3 threes are 9
• 3 fours are 12
• 3 fives are 15 …

Now, let’s add these two tables together to create a new table. We’ll add the values of the same number from both tables.

Table of 2 + Table of 3:

• 2 ones (from Table of 2) + 3 ones (from Table of 3) = 5 ones
• 2 twos (from Table of 2) + 3 twos (from Table of 3) = 5 twos
• 2 threes (from Table of 2) + 3 threes (from Table of 3) = 5 threes
• 2 fours (from Table of 2) + 3 fours (from Table of 3) = 5 fours
• 2 fives (from Table of 2) + 3 fives (from Table of 3) = 5 fives …

By adding the values from the Table of 2 and the Table of 3, we created a new table where each number is the sum of the corresponding numbers from the original tables. This is how we can make tables from tables in mathematics!Story Time: Sharing

• Once upon a time, there was a girl named Jaya. 
• She had two younger twin brothers, Rohan and Aryan. 
• One day, Jaya’s mother baked yummy cookies and put them on a plate. 
• She asked Jaya to share the cookies equally with her brothers. 
• Let’s see how Jaya did it step by step in a very easy way.

Step 1: Jaya looked at the plate and counted cookies, there were nine cookies.

Step 2: She thought, “I have to give some cookies to Rohan and Aryan so that we all have the same.“

Step 3: Jaya took three cookies from the plate and gave one cookie to Rohan, one to Aryan, and kept one for herself. Now each of them had one cookie.

Dividing one cookie each

Step 4: Next, Jaya took two more cookies from the plate and gave one to Rohan and one to Aryan. She kept one cookie for herself again. Now each of them had two cookies.

Dividing 2 cookies each

Step 5: Finally, Jaya saw that there were four cookies left on the plate. She gave one cookie to Rohan, one to Aryan, and kept two cookies for herself. Now each of them had three cookies.

Everyone getting 3 cookies

Jaya smiled and said, “Look, Rohan, Aryan, and I each have three cookies. We all have the same number of cookies, and everyone is happy!”

• Jaya’s mother was very proud of her for sharing the cookies equally and making sure everyone got their fair share. 
• Jaya learned that sharing is caring, and dividing things equally makes everyone happy.

Hey kids! today we’re going to learn something exciting through a story! Get ready to discover how measurement works in a fun and engaging way!

Story Time: Raja and CarpenterRaja Jagdeep’s Request

• Raja Jagdeep wanted to make a beautiful carved bed for his queen.
• He asked his best carpenter to make the bed 10 handspans long.
• The carpenter made the bed 10 handspans long, but the queen was unable to fit in.
• When the king measured the bed, he found it was only 8 handspans long.
• The king was confused and asked someone else to measure the bed again.
• This time, the bed measured 14 handspans!

The Confusion

• Everyone is puzzled: Why do the measurements differ?
• The Mantri (minister) explains that the length of a “hand-span” varies with each person’s hand.
• To measure fairly, they decide to use the same hand-span (for example, the carpenter’s) every time.

Understanding Measurement: What is it?

Measurement is the process of finding out the size, length, weight, or capacity of something. We use measurements in our daily lives without even realizing it. Whether it’s figuring out how tall we are, how heavy a bag is, or how much water is needed to fill a pot, we use measurements all the time.

Measurement of Length, Weight and CapacityThis chapter focuses on three main types of measurement:

1. Length – how long or short something is.
2. Weight – how heavy or light something is.
3. Capacity – how much something can hold (usually liquids).

Let’s explore each of these in detail.

Distance- How far?

Measuring distance is like counting steps or jumps to find out how far things are from each other on a grid or map. We use units of distance, like meters or feet, to measure the length or distance between two points.

Let’s help Shinchan

Now Let’s help shinchan to reach masao’s home using shortest distance. 

• To find the shortest distance, we are using a grid. 
• Imagine a grid with horizontal and vertical lines.  Each line, whether going up and down (vertical) or left and right (horizontal), is like taking a single step or jump. 
• We call each of these lines a unit of distance. 
• So, if you want to measure how far something is from one point to another, you count how many of these lines you need to go across or up and down.
  Shinchan & Masao

For instance, if you start at one corner of the grid and move three lines to the right (horizontal) and two lines up (vertical), you’ve moved a total of five units of distance. It’s like counting steps or jumps, but instead, we’re counting the lines in the grid.

Imagine Shinchan wants to visit Masao’s house on a grid. If he starts moving diagonally upwards, he’ll eventually reach Masao’s house. However, there are many other paths he could take to get there.

That’s where the grid comes in handy. It helps us figure out how many units of distance each route to Masao’s house will take. We use the grid to compare and find the shortest distance possible.

• For example, let’s say there are two routes. 
• In route one, it takes 10 units of distance for Shinchan to reach Masao’s house. 

• But in route two, it only takes 6 units of distance.

Route 2

• Now, which route should Shinchan pick? The correct answer is route two, because 6 units of distance are lesser than 10 units. So, using the grid helps us make smart decisions and find the shortest route. Cool, right?

Height- How Tall?

“How Tall?” is about measuring how high or tall something or someone is, like a tree or a person. We use units of measurement, like meters or feet, to find out the height from the ground to the top of the object or person.

Story Time: How tall we are?

Once upon a time in a park, there were boxes of flowers piled up high, forming a huge tower. 

• All the kids gathered around to see how tall they were compared to the tower. 
• Rajat stood next to the tower and found out he was 4 boxes tall.
   Rajat is 4 boxes tall
• Richa then stood beside Rajat and discovered she was 5 boxes tall. 
  Richa is 5 boxes tall
• Finally, Disha joined them and realized she was 3 boxes tall.
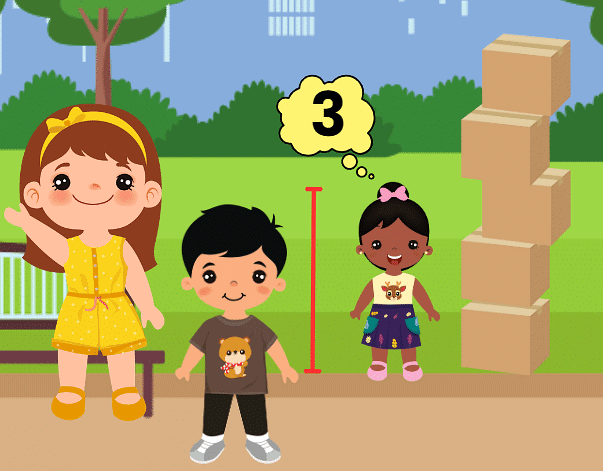  Disha is 3 boxes tall
• The kids were amazed to see how the tower helped them understand their heights in a fun way. 
• They learned that comparing our height to something else, like a tower or a tree, can show us how high or tall we are.

Weight- Heavier or lighter?

“Heavier or lighter?” is about comparing the weight of different objects to see which one is heavier (weighs more) or lighter (weighs less) than the other.

• When we say that one vegetable is heavier than another, it means that it weighs more. 
• For example, if a pumpkin weighs 5 kilograms and a cucumber weighs 1 kilogram, we can say that the pumpkin is heavier than the cucumber.

Pumpkin is heavier than cucumber

• On the other hand, when we say that one vegetable is lighter than another, it means that it weighs less. 
• For example, if a potato weighs 1 kilograms and a watermelon weighs 2 kilograms, we can say that the potato is lighter than the watermelon.

Potato is lighter than watermelon

Capacity – How much?

Capacity or “how much” refers to the amount of space something can hold or the amount of something it can contain. For example, a glass can hold 250 milliliters of water, showing its capacity, or a bucket can contain 5 liters of sand, indicating how much it can hold.

Capacity of glass & bucket

Story time: Tanya and the Bucket

• Once upon a time, there was a curious and helpful girl named Tanya. 
• One day, her mom asked her to fill a big bucket with water from a tap using a mug. 
• Tanya was excited to help and started filling the mug with water from the tap.

• As she poured the water from the mug into the bucket, she noticed that the mug could only hold a small amount of water each time. 
• After filling the bucket several times with the mug, Tanya realized that the bucket had a greater capacity than the mug. 
• This means the bucket could hold much more water compared to the mug.

• Tanya learned that capacity is about how much a container can hold. 
• The mug had a smaller capacity because it could only hold a little water, while the bucket had a larger capacity as it could hold a lot more water. 
• Tanya felt proud of herself for understanding the concept of capacity and helping her mom with the task.

Learning about measurement helps us compare things, guess how much there is, and solve problems, which makes our daily tasks easier and more accurate! Just like tanya,

Tens and Ones

Hello kids!

Let’s understand grouping and the mathematical concept of ones and tens with the help of Raj and Maya.

• Raj and Maya, two friends who love making beautiful bracelets.
  
• Each bracelet they make has 10 flowers on it, and sometimes they give some extra flowers along with the bracelet. 
• Let’s see how we can use grouping to understand addition with ones and tens.
• Raj and Maya made three bracelets together. 
• The first bracelet had 10 flowers, the second bracelet had 10 flowers plus 2 extra flowers, and the third bracelet had 10 flowers plus 5 extra flowers.

Understanding Ones and Tens:

• Ones: Ones refer to single units or individual items. For example, single (extra) flowers, like the extra flowers Raj and Maya gave with the bracelets.
• Tens: Tens are groups of ten items or objects. For example, groups of 10 flowers, like the 10 flowers on each bracelet.

For example: for the bracelet in which there 10 flowers in bracelet & 2 extra flowers,  there will be 1 tens and 2 ones. 

1 tens means 10 flowers and 2 ones means 2 flowers.

Counting the Flowers

First Bracelet: 10 flowers (10 in tens, 0 in ones).

Second Bracelet: 10 flowers (10 in tens, 0 in ones) + 2 extra flowers (0 in tens, 2 in ones) = 12 flowers (10 + 2).

Third Bracelet: 10 flowers (10 in tens, 0 in ones) + 5 extra flowers (0 in tens, 5 in ones) = 15 flowers (10 + 5).

Adding Ones and Tens

• Adding Ones: Raj and Maya gave 2 extra flowers with the second bracelet and 5 extra flowers with the third bracelet. So, 2 ones (from the second bracelet) + 5 ones (from the third bracelet) = 7 ones.
• Adding Tens: Raj and Maya made 3 bracelets, each with 10 flowers. So, 3 tens (10 + 10 + 10) = 30.

By grouping the flowers into tens and ones, we can easily add them together. In total, Raj and Maya gave 7 extra flowers (7 ones) and made 30 flowers in bracelets (3 tens). Grouping helps us understand addiction better and makes counting and adding more fun!

Let’s Learn about Numberline now! Imagine a number line as a magical road that helps us understand numbers better. It’s like a big ruler, but instead of measuring length, it shows us how numbers go from small to big or big to small.

What is a Number Line?

A number line is like a long path with numbers written on it. The numbers start from the smallest on the left and get bigger as we move to the right.

Number Line

Fruits on the Table 

Imagine you have a line of fruits on a table:

• At one end, there’s an apple (0).
• Next to it, there’s a banana (1).
• Then, an orange (2).
• Followed by a pear (3).

If you point your finger at apple and more 2 steps ahead, 

you will end up on orange. 

The fruit line helps us understand how numbers go in order. It’s like taking a tasty journey through math!

when we jumped from apple , with number 0, to orange, with number 2, we added numbers on our imaginary fruit number line. 0+2=2 and that’s where our finger was pointed when we jumped 2 steps ahead. 

If we take 1 step back from where we are now, let’s see where we land now.

When we took back a step, we ended up on banana, which is at number 1. we can also say 2-1 = 1. That’s how we subtract numbers on number line.

Adding and Subtracting Tens on the Number Line

Imagine you have a special number line with big steps, each step representing ten numbers:

• At the start of the number line, there’s a sign for 0 tens (0).
• One big step ahead, there’s a sign for 1 ten (10).
• Two big steps ahead, there’s a sign for 2 tens (20).
• And so on, with each big step representing ten more numbers.

• If you start at the sign for 0 tens (0) and take two big steps ahead, you’ll land on the sign for 2 tens (20).

Adding Tens

When we took two big steps from 0 tens to 2 tens, we added numbers on our big-step number line. 0 + 2 = 2 tens (20), and that’s where we landed after taking two big steps ahead.

Subtracting Tens

Now, let’s go back one big step from where we are, from 2 tens (20) to 1 ten (10).

• When we took one big step back, we ended up on the sign for 1 ten (10). 
• We can also say 20 – 10 = 10, which is 1 ten. 
• That’s how we subtract numbers on the big-step number line.

The big-step number line helps us see how numbers change when we add or subtract tens. It’s like taking big leaps in math and exploring numbers in a fun way!

Now that we understand how ones and tens work, let’s practice adding and subtracting them. 

Let’s Learn Addition by Practicing

Imagine Ram has 24 coins in his collection, with each coin worth 1 rupee. He receives an additional 32 coins.

Understanding Ones and Tens

• Ones: Ram starts with 24 coins, which means he has 2 tens (20 coins) and 4 ones (4 coins).

• Adding More Coins: Ram receives 32 additional coins, which means he’s adding 3 tens (30 coins) and 2 ones (2 coins) to his collection.

Calculating Total Coins

• Original coins: 2 tens (20 coins) + 4 ones (4 coins) = 24 coins
• Additional coins: 3 tens (30 coins) + 2 ones (2 coins) = 32 coins

He added additional 3 tens into 2 tens he had and similarly added additional 2 ones to 4 ones he had

After adding the new coins, Ram has 5 tens (50 coins) and 6 ones (6 coins) in his collection, having total of 56 Rs. This way, he learns how to count and add tens and ones when receiving additional coins!

Now, let’s explore Subtraction. 

Let’s Learn Subtraction by Practicing

Imagine Ram has a collection of coins. He has 37 coins in total, with each coin worth 1 rupee. Ram decides to buy himself a snack from the store, which costs 23 coins.

Understanding Ones and Tens

• Ones: Ram starts with 37 coins, which means he has 3 tens (30 coins) and 7 ones (7 coins).

• Buying the Snack: The snack costs him 23 coins. This means he’s spending 2 tens (20 coins) and 3 ones (3 coins) on the snack.

Calculating Remaining Coins

To find out how many coins Ram has left, he subtracts the coins spent on the snack from the coins he had originally:

• Original coins: 3 tens (30 coins) + 7 ones (7 coins) = 37 coins
• Coins spent on snack: 2 tens (20 coins) + 3 ones (3 coins) = 23 coins

He subtracted 2 tens from 3 tens and then subtracted 3 ones from 7 ones

• Remaining coins: 1 ten (10 coins) + 4 ones (4 coins) = 14 coins

After buying the snack, Rama has 1 ten (10 coins) and 4 ones (4 coins) left in his collection. This way, he understands how to count and subtract tens and ones when dealing with money!

Remaining coins

Addition Pyramid

Let’s Practice and learn addition with help of a pyramid. Observe the following pyramid:

Here, the 2 numbers at the base are getting added to form the number above them. 

• 5 and 3 are added to make 8.
• Similarly 6 and 8 are added to make 14. 

• To find the missing number above 3 and 6, we must follow the pattern we have observed and add 3 and 6.
• 3 + 6 make 9, so the missing number above 3 and 6 will be 9. 

• Now let’s guess next number.
• Number above 8 and 9 will be their sum, so 8 + 9 = 17, thus the number is 17.
  
• Similarly, number above 14 and 9 will be 14 + 9 = 23, thus the nuber is 23.

• Now its time to find the top of the pyramid. 
• To find it, we will again follow the pattern and add 17 and 23.

• 17 + 23 = 40, thus top of pyramid is 40. 

Great Job! kuddos we have completed the pyramid ✨

Subtraction Pyramid

Let’s Practice and learn subtraction with help of a pyramid like we practiced addition. Observe the following pyramid:

Here, number below the bigger number is being subtracted from the number above it.

To find the 1st missing number, we need to subtract 24 from 50. Thus the number is 26.

To find next missing number, we need to subtract 11 from 26. Thus 26 – 11 = 15. making the missing number 15.

To find next number we will repeat the same process , 24 – 11 = 13.

• Great job! we are almost there, let’s find last missing numbers.
• Subtract 9 from 15, so the missing number is 15 – 9 = 6.
  and to find last number, subtract 5 from 13, thus 13 – 5 = 8, so last missing number is 8. 

With all the Practice we have now learned how ones and tens work and how they make addition and subtraction easy. 

Exploring Lines

Hey there, little explorers! Today, let’s discover the fascinating world of lines.

Beach

Let’s understand lines with help of a story.

Story: The Seashell Hunt

Once upon a time, a group of friends decided to go on a seashell hunt at the beach. They walked along the shore, and as they looked down, they noticed something interesting.

“Look!” exclaimed Sarah, pointing at the sand. “What are these lines?“

Lines forming on the beach

“These are lines made by the waves,” explained Alex, the curious explorer of the group. “They come and go, leaving behind these beautiful lines in the sand.”

As they continued their adventure, they found different types of lines:

• Standing Lines: Like the beach umbrellas standing tall and straight against the wind.

Umbrella forming Standing line

• Sleeping Lines: Imagine the seashells resting peacefully on the shore, forming sleeping lines.

Shells forming Sleeping lines

• Slanting Lines: Picture the crabs’ trails as they move sideways, creating slanting lines in the sand.

Crab forming Slanting line

You already know about sleeping straight and slanting lines. Now, let’s discover more about four special types of lines ✨

Vertical Line

A vertical line goes straight up and down, just like a tall tower reaching for the sky. Standing lines are called vertical lines. 

Vertical line

Example: Imagine a standing stick or a towering tree. They are like vertical lines, standing tall and straight.

Vertical tree & tower

Horizontal Line

A horizontal line goes straight across from left to right, like a line drawn on the ground. Sleeping lines are called Horizontal lines.

Horizontal Line

Example: Think of the horizon where the sky meets the land or a flat table. They are like horizontal lines, stretching from side to side.

Horizontal table

Here, the table has both Horizontal as well as Vertical lines. Legs of the table is Vertical where as top is Horizontal. Similarly, objects can have multiple lines as well. 

Slanting Line

A slanting line goes diagonally from one side to another, like a ramp going up a hill.

Slanting Line

Example: Picture a ladder leaning against a wall or a slide sloping down. They are like slanting lines, leaning or tilting.

Slanting ladder

Curved Line

A curved line is not straight; it bends or curves. 

Curved Lines

Example: Imagine a smiley face with its curved mouth or a rainbow arching across the sky. They are like curved lines, flowing and bending in a gentle curve.

Learn by Practicing – 1

Let’s Try to Count Different Types of Lines!

Once upon a sunny day, Raju decided to explore his garden. 

• As he wandered among the trees and flowers, he stumbled upon a collection of sticks scattered on the ground. 
• Raju’s eyes sparkled with curiosity as he thought, “Hmm, I wonder how many different types of sticks I have here!”

Let’s see how Raju counted sticks;

Step 1: Identifying Straight Sticks

Raju began by picking up the sticks one by one. He noticed that some sticks were standing tall and straight, just like vertical lines. He gathered all these sticks and placed them in a neat pile.

Identify Straight sticks

Step 2: Identifying Curved Sticks

Next, Raju searched for sticks that were not straight but had gentle curves or bends, similar to curved lines. He carefully separated these curved sticks from the rest and arranged them beside the straight sticks.

Identifying Curved Sticks

Step 3: Counting the Sticks

With the straight sticks and curved sticks neatly arranged, Raju began counting. He counted each group of sticks one by one, starting with the straight sticks.

Counting straight sticks

• “1, 2, 3, 4… Wow, I have 6 straight sticks!” Raju exclaimed happily.
• Then, Raju moved on to count the curved sticks.

Counting curved sticks

• “1, 2, 3… Look, I have 3 curved sticks!” Raju exclaimed, delighted with his discovery.
• Raju learned that lines are not just in books or on paper but can be found in nature too, like in the sticks he found in his garden. 

Learn by Practicing – 2

Now Let’s Help Charu in counting different types of lines. Look closely and tell how many vertical, horizontal, slanting, and curved lines you can find!  

1. Let’s Start by finding & counting Vertical lines
   
   Look there are 1, 2 & 3 Vertical lines.
2. Now let’s try to count Slanting lines
   
   There are 2 Slanting lines.
3. Let’scount Horizontal lines next.
   
   See, there are 4 Horizontal lines.
4. Now let’s see how many Curved lines are there
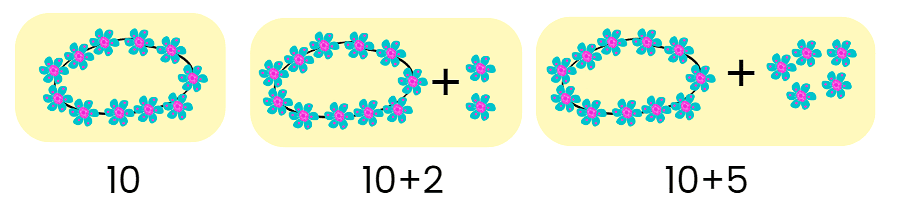
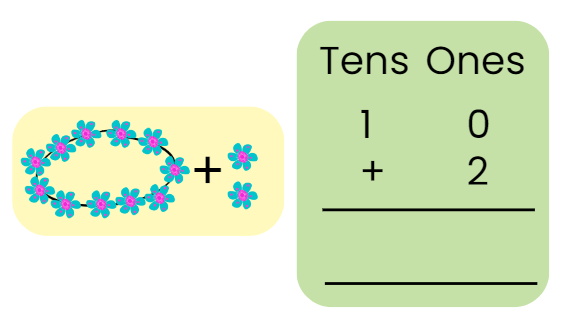
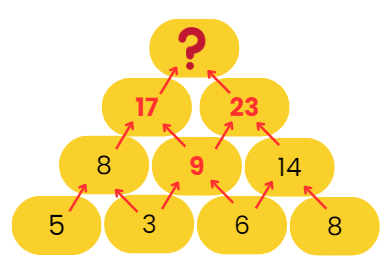
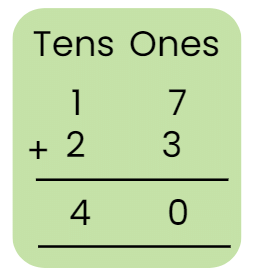
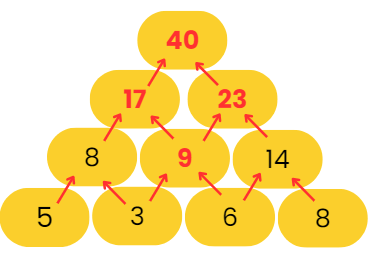
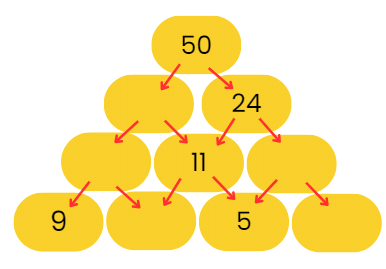
   There is only 1 Curved line.

Great job! In the picture, there are:

• 3 vertical lines
• 2 slanting lines
• 4 horizontal lines
• 1 curved line

You did an amazing job counting and exploring the lines in the image! 

Nakul and his friends saw a shadow play called Togalu Gombeyaata at a village fair. 
They were all fascinated by the moving shapes and stories told with only light and shadow. 

Let’s learn in this chapter about shadows, different shapes, and fun patterns!

Story Time: Sahil’s Shadow Adventure

Hey kids, today let’s go on a fun journey with Sahil into the world of shadows.

• Sahil was a curious boy. 
• One evening, when his mom lit a candle, Sahil saw something cool.
  
• When he walked past the candle, he saw shapes on the walls. 
• He asked his mom, “What are these shapes?”

• Mom said, “Those are shadows, Sahil. They come when something blocks the light.”
• Excited, Sahil tried making shapes with his hands in front of the candle. He made a bird, a heart, and a funny face. Each time, a shadow showed up on the wall.
  
• Then Sahil took his ball and put it between the candle and the wall. The ball made a circle shadow. Sahil said, “Look, a circle shadow from the ball!”
  Circle Shadow made by Ball
• Next, he got his birthday cap and put it near the candle. The cap’s shadow looked like a tall cone. Sahil laughed, “My cap’s shadow is like a Triangle!”
  Triangle Shadow made by Birthday cap
• Sahil also tried his geometry box. Its shadow was a rectangle. He said, “The box makes a straight shadow, just like its shape!”

Rectangle Shadow made by Geometry boxSahil had so much fun exploring shadows with different things. He learned that each thing makes a special shadow based on its shape. And that’s how Sahil’s shadow adventure taught him about different shapes as well.

From Sahil’s adventure, we have explored the amazing world of shapes. Let’s Learn more!

Shapes

Shapes are like the building blocks of everything around us. They can be round like a ball, have four sides like a square, three sides like a triangle, or even more sides like a rectangle. They help us understand and describe the world in a fun and interesting way!

There are different types of shapes, Let’s learn about them.

Different Shapes
There are many types of shapes. Some have straight sides like squares, rectangles, and triangles. Others, like circles and ovals, have curved sides. Each shape has its own special features!

1. Square: A square has four equal sides. Imagine a perfect square cookie with all sides the same length. It’s like a perfect box or a checkerboard tile.
Square

2. Rectangle: Similar to a square, a rectangle has four sides, but its opposite sides are equal in length. Imagine a door or a window—it’s taller or wider than a square, but it still has those right angles.
Rectangle

3. Triangle: Imagine a triangle like a slice of pizza or a big pointy hat. It has three sides and three corners. You can find triangles in Pizza slice, birthday cap , just like sahil. Triangle

4. Circle: Think of a circle as a perfectly round ball. It doesn’t have any corners or edges. When you draw a circle, it goes around and around, just like the wheels on a bicycle!

Circle5. Oval: An oval is like a stretched-out circle. It’s not perfectly round but still smooth and curved, like an egg or a rugby ball.

Oval

Now that we know about shapes, Let’s help Aanya to colour the rangoli.

Learn by Practicing- Aanya’s Rangoli

• Once upon a time, there was a girl named Aanya who loved coloring and creating beautiful artwork. 
• One day, she opened her coloring book to a page with a lovely rangoli design. 
  Aanya
• The design was filled with different shapes like circles, squares, and triangles, each waiting to be colored .
• Let’s see how Aanya coloured the rangoli.

Step 1: Aanya looked at the rangoli design and decided to start with the circles.

Rangoli

Step 2: Checking the instructions in her coloring book, Aanya found that circles were supposed to be blue.
Instructions

Step 3: With her blue crayon in hand, Aanya carefully identified the circle in the rangoli pattern and colored it beautifully in blue.

Step 4: Moving on to the squares, Aanya checked the instructions again. Squares were meant to be green.

Step 5: Aanya smiled and started coloring the squares with her bright green crayon, filling each square with cheerful green color.

Step 6: Lastly, Aanya looked for the triangles in the rangoli. According to the instructions, triangles were to be yellow.

Step 7: Taking her yellow crayon, Aanya added a touch of yellow to each triangle, completing the colorful and vibrant rangoli design.

As Aanya stepped back to admire her work, she felt a sense of pride and happiness. The rangoli looked stunning with its blue circles, yellow squares, and green triangles, creating a harmonious and delightful artwork.

With Aanya’s colouring activity we got to practice shapes. Let’s move on and learn about Patterns.

Patterns

Patterns are like beautiful designs that repeat in a special way. 

• Imagine you have a line of colorful blocks: red, blue, green, red, blue, green, and so on.
  
• This is a pattern because it keeps repeating in the same order: red, blue, green, red, blue, green.
• Patterns can be made of shapes, colors, or even with numbers.
• They can be found in nature, like the stripes on a zebra or the petals on a flower.
  

Learning about patterns helps us understand how things repeat in a predictable way, which is super fun and interesting!

Now that we know what patterns are, Let’s go on an adventure with Kunal.

Learn by Practicing- Kunal’s fruity pattern

• Once upon a time, there was a boy named Kunal who loved organizing things. 
• One sunny day, he decided to arrange his favorite fruits on the kitchen table. He had some juicy mangoes, shiny apples, and sweet pears.
  
• Instead of putting them all in one group, Kunal wanted to create something special. 
• He thought for a moment and then arranged them in a pattern. First, he placed an apple, then a mango, and after that, a pear.
  
• But when he tried to continue the pattern, he got a bit confused. Kunal wanted the arrangement to look beautiful and repeat in a special way, but he wasn’t sure how to do it.
• Just then, his older brother Raj walked into the kitchen. Raj was good at solving puzzles and figuring out patterns. Kunal asked for his help, “Raj bhaiya, can you help me make a pattern with these fruits?“
  
• Raj smiled and said, “Of course, Kunal! Let’s see what you’ve done so far.” He looked at the fruits on the table and noticed the arrangement: apple, mango, pear.
• Raj said, “You’ve already started a pattern! You just need to repeat what you’ve created.” He picked up another apple and placed it next to the pear. “Look, now it’s apple, mango, pear, apple. That’s a pattern!”
  
• Kunal’s eyes lit up with excitement. He understood now. With Raj’s guidance, they continued the pattern: apple, mango, pear, apple, mango, pear, and so on.
  

By creating this fruity pattern, Kunal learned how repeating a sequence can make things look organized and interesting. 

Number Patterns

Patterns can be anywhere, even in numbers. 

• Imagine you can block of different numbers from 1 to 6 arranged in a line.
  
• If you keep 1 and remove 2, then keep 3 and remove 4 and continue the pattern,  keep 5 and remove 6, then you will end up with a pattern of numbers where 1 number is being skipped. 
  
• There are many ways to form number patterns.

Keep looking for different patterns around you and see how you can continue them.

Look at the picture and observe different musical instruments:

• Everything we see in the world around us has a shape. 
• ​If we look at musical instruments, we can see how they all are similar to a shape.
• Students, let us help Maria match the musical instruments in the music room of her school to the shapes they match. 

• The clarinet resembles a cone.
• Harmonium matches the shapes of a cuboid.
• Dholak resembles the shape of a cylinder.
• The tambourine matches the shape of a circle. 

Musical instruments are tools we use to make music. Just like tools in a toolbox, each instrument has its own job and sound.
For example, a guitar has strings that we strum to make music, while a drum lets us tap out beats with sticks.
There are different types of instruments. Some you blow into, like a flute or a trumpet, and they make sound when air passes through them. Others you hit or shake, like drums or maracas, to make different sounds.
Each instrument has its own unique shape, size, and sound. Some are big and loud, like a piano, while others are small and delicate, like a violin.

Let us now revise the concept of 2D Shapes 

2D Shapes

2D shapes can be defined as plane figures that can be drawn on a flat (or plane) surface or a piece of paper.

1. Circle: A circle is a round shape on a flat surface. It’s like a big loop that goes around and around. Imagine there’s a special point right in the middle of the circle, called the “center.” Every point on the circle is the same distance away from this center point. 
2. Triangle: A triangle is a three-sided polygon (2D Shape) which has three edges and three vertices. The sum of all the three angles of a triangle is equal to 180°. 
3. Square: A square is a four-sided polygon (2D Shape), whose four sides are equal in length and all the angles are equal to 90°.
4. Rectangle: A rectangle is a 2D shape which has four sides, where the opposite sides are equal and parallel to each other. 
5. Pentagon: A pentagon is a shape with five sides, like a house on paper. It can look the same on all sides (regular) or different (irregular). When it’s regular, each corner inside the shape is 108 degrees, and each corner outside the shape is 72 degrees. 
6. Octagon: An octagon is an eight-sided polygon which can be either regular or irregular. It is a 2d shape which has eight angles. The sum of all the interior angles of an octagon is 1080°. 

What are 3D shapes?

• Imagine you have special shapes that aren’t flat like paper. 
• These shapes take up space all around, and we call them 3D shapes because they have three dimensions: length, height, and width.
   
• It’s similar to holding a toy or a block that you can touch and feel from all sides. 
• Now, you might know about 2D shapes, such as squares and circles, which are flat, like drawings on paper. 
• Well, 3D shapes are different because they’re not flat. Instead, they’re real objects that you can hold because they occupy space in three different ways.

• Some examples of 3D shapes include cubes (similar to dice), pyramids (like the top of a triangle tower), spheres (like a ball), and cones (like an ice cream cone). You can find these shapes all around you—in toys, buildings, and even in your snacks, such as cookies and fruits!
• Look at the shapes given below and see how they match the shapes.
  

What are some Different 3D shapes?

Here are some common examples of different 3D shapes that you should know about. Take a look at the image below to see what they look like:

• Sphere (3D circle)
• Cube (3D square)
• Square Pyramid (3D triangle with a square base)
• Cuboid (3D Rectangle)
• Cylinder (3D shape with a circular base)
• Triangular Prism (3D shape with identical triangle bases)
• Cone (3D triangle with a circular base)

Odd One OutLet us play a game.
Given below are images of a few objects. Can you identify which is the odd one out?

“Odd one out” means finding the one thing that is different or doesn’t belong in a group. It’s like playing a game of “spot the difference” where you look at a group of things and find the one that doesn’t fit with the others.

First is the sun, then a globe, a building and a ball.
Now, we can see that the sun, globe and ball, all match the shape of a circle. The building is not circular in shape.
Hence, building is the odd one out.
Well done students!

What are the Properties of Different 3D shapes?

All three-dimensional shapes are different but have three primary properties in common. These main 3D shape properties include:

• Faces: Faces are flat surfaces on the shape.
  A face is a flat or curved surface on a 3D shape.
  For example, a cube has six faces, a cylinder has three and a sphere has just one.
• Edges: Edges are straight lines that define the sides of the polygons that make up each face of the shape.
  An edge is where two faces meet. For example, a cube has 12 edges, a cylinder has two and a sphere has none.
• Vertices: Vertices (or corners) are points where at least three edges meet.
  A vertex is a corner where edges meet. The plural is vertices. For example, a cube has eight vertices, a cone has one vertex and a sphere has none.

Have a look at the picture below, which shows these key parts of 3D shapes. A cube is taken as an example, but we can apply this knowledge to other three-dimensional shapes, too.

This is also an example of a net. A net shows what 3D shapes would look like if it was taken apart and flattened.
When a cardboard box is constructed, it is a 3D shape – a cuboid or a cube. When it is flattened, it becomes a 2D net, which is like an irregular 2D shape.
Now, let’s talk about the properties of 3D shapes! These are the special things about each shape that make them unique. For example:

• Properties of a Sphere (2D – Circle)
  
• Properties of a Cube (2D – Square)
  
• Properties of a Square Pyramid (2D – Triangle and Square)
  
• Properties of a Cuboid (2D – Rectangle)
  
• Properties of a Cylinder (2D – Circle)
  
• Properties of a Triangular Prism (2D – Triangle)
  
• Properties of a Cone
  

You can pick everyday objects, which you are familiar with or would have seen in comics or cartoons:

• a ball– a great example of a sphere;
• a Rubik’s cube or a die– examples of a cube;
• a party hat– an example of a cone;
• the Egyptian pyramids – an example of square-based pyramids.

Can you now notice the difference between a ball for example and a circle drawn on a piece of paper?

Yes, you are right, now you are able to tell that the ball on the right is real and 3D in shape. And What’s the shape? Yes, you are right again, it’s a Sphere; while the one on the right is a 2D shape of circle drawn on a paper.

Students, look around your surroundings and look at different objects. Try matching them to shapes and count how many faces, edges and vertices they have.
Look at the table below, we have taken a few of the objects that you see in your daily life and have mentioned the number of faces, edges and vertices.

Corners

Let’s go on a fun adventure to find objects with different numbers of corners!

No Corners:
Let’s think about things that are super round and don’t have any corners at all.

A. Balloon

B. Cloud

C. Soap Bubble

One Corner:
Now, let’s search for something with just one little corner. Hmm, what could it be?
A. Pyramid
B. Mountain
C. Icecream

Three Corners:
Okay, last but not least, let’s find something with three corners. Hmm, where could we find that?

A. Triangle road sign

B. Pizza slice

C. Flag

Hope you’ll continue to look around your surroundings with curious eyes. You’ll be amazed at how many fascinating shapes and objects you can find! Whether it’s a round ball, a triangular slice of pizza, or a rectangular door, shapes are everywhere, waiting to be discovered. So, keep exploring and noticing the world around you. Who knows what interesting shapes you’ll find next!