Mathematics for Class 3 ( Maths Mela ) Chapter Notes

Have you ever noticed the door in your classroom, a slice of pizza, or your school clock?

• All of these are shapes—the building blocks of everything around us!
• Today we will look, draw, and play with four shapes:
  1. Rectangle
  2. Square
  3. Triangle
  4. Circle

Let’s begin our shape adventure!

Rectangle

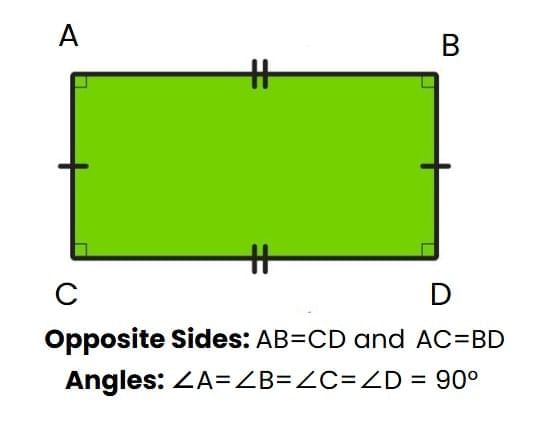
A rectangle is a shape with four sides where opposite sides are the same length, and all the angles are right angles.

Try yourself:

Which of the following objects is most likely to be in the shape of a rectangle?

• A.Soccer Ball
• B.Book
• C.Clock
• D.Pizza

View Solution

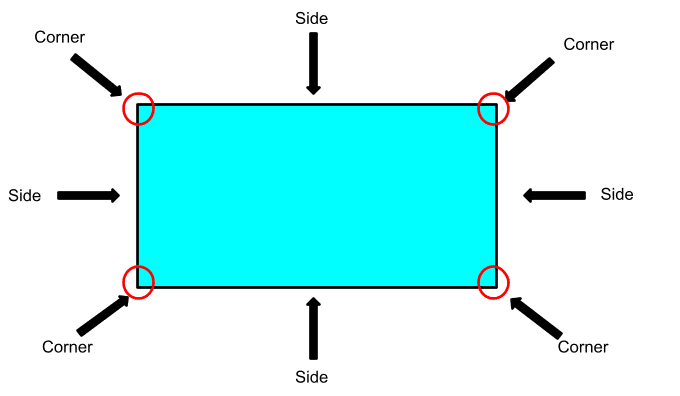
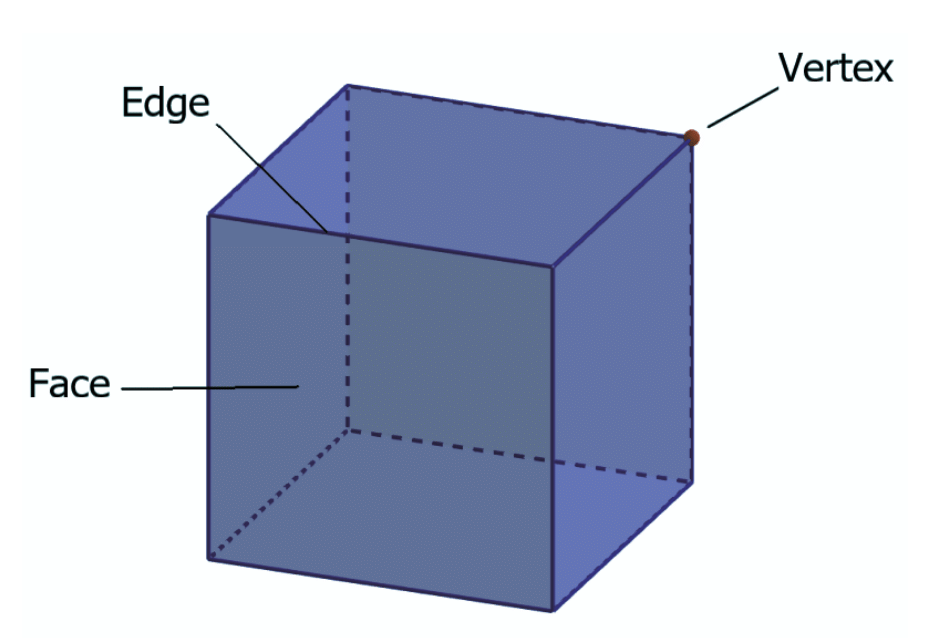
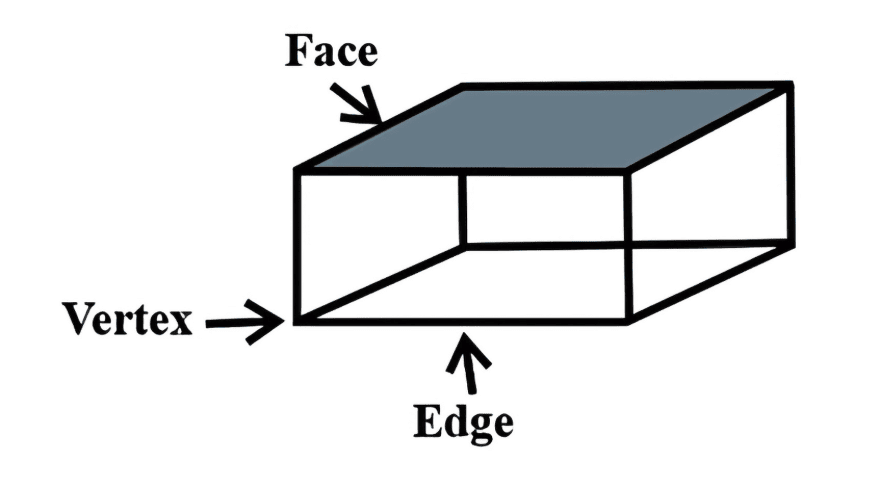
Parts of a Rectangle:

• Sides: Rectangles have four sides. The longer sides are called the length, and the shorter sides are called the breadth.
• Corners & Angles: Rectangles have four corners where two sides meet at right angles, giving the shape a sharp and clear look.

Common objects that are rectangles include a blackboard, a TV screen, and a ruler. These items are often found in our daily lives and have specific uses.

Rectangles Around Us

Square

A square is a unique kind of rectangle and also a four-sided shape where all four sides are the same length.

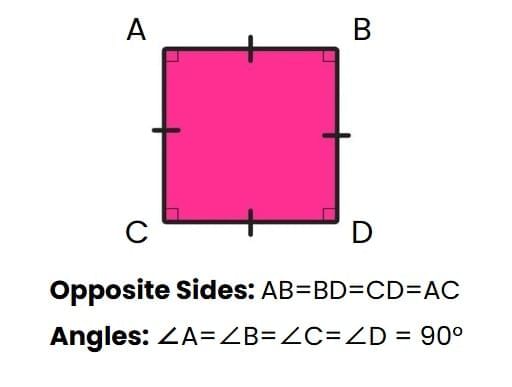
Parts of a Square:

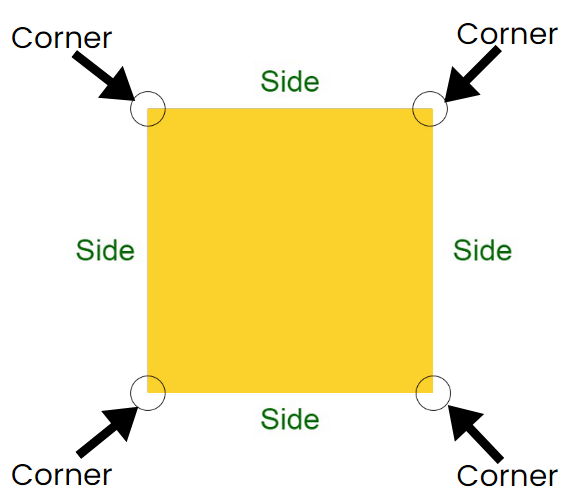
• Sides: Squares have four equal sides, meaning each side is the same length.
• Corners: The corners of a square form right angles (90 degrees).

For Example– Chess Board, Carrom Board , Clock

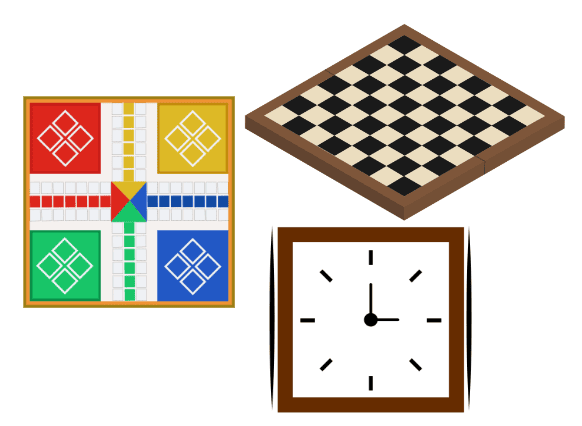
Squares around us

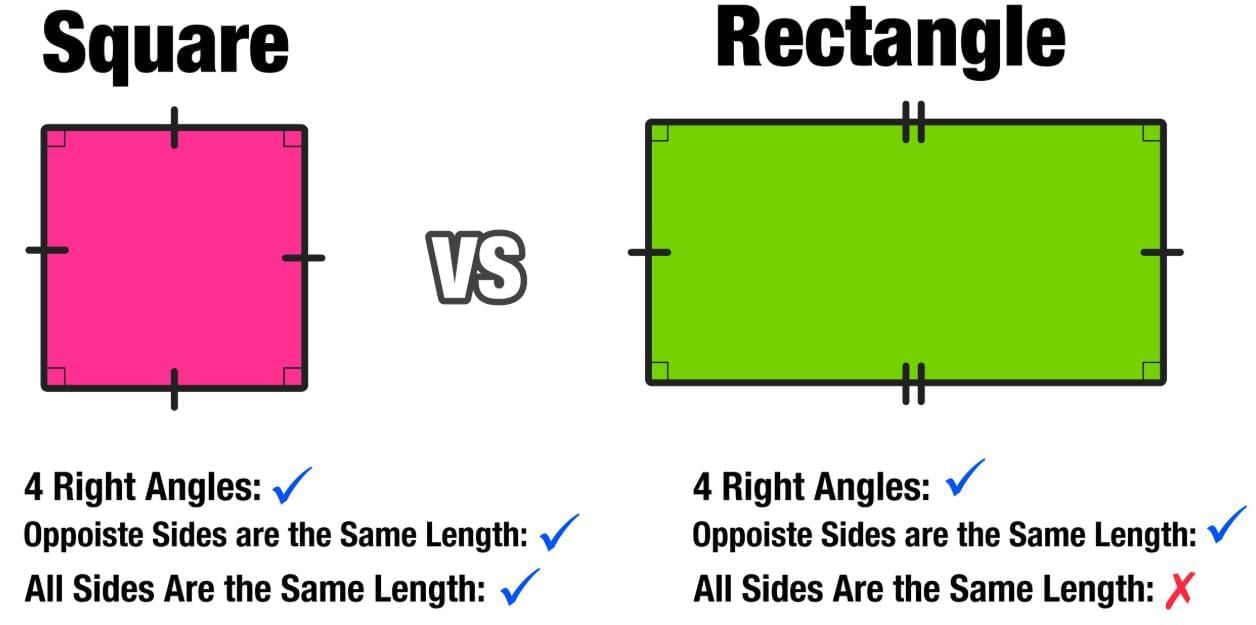
Similarities and Differences in Rectangle and SquareA rectangle and a square are both flat shapes with four straight sides and four corners. In fact, a square is just a rectangle that has all its sides the same length! Here’s what they share:

• Four sides
  Both shapes have exactly four straight sides.
• Opposite sides the same length
  In each shape, the top and bottom sides match in length, and the left and right sides match too.
• Four right-angle corners
  Every corner in a rectangle or a square is a “right angle” (just like the corner of a book).
• Remember:
  Every square is a rectangle because it follows all these rules.
  But not every rectangle is a square, since rectangles only need their opposite sides to be equal—not all four.

Triangle

A triangle is a shape with three sides and three corners. It looks like a slice of pizza or a traffic sign.

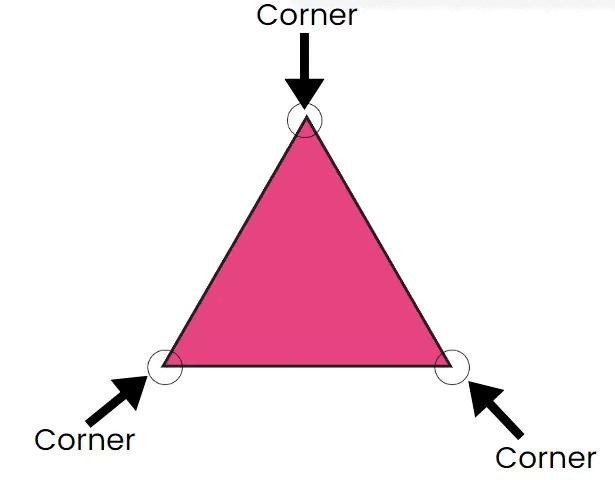
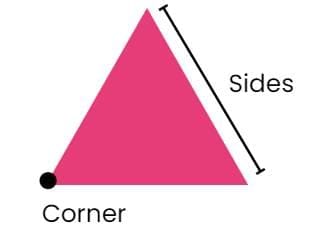
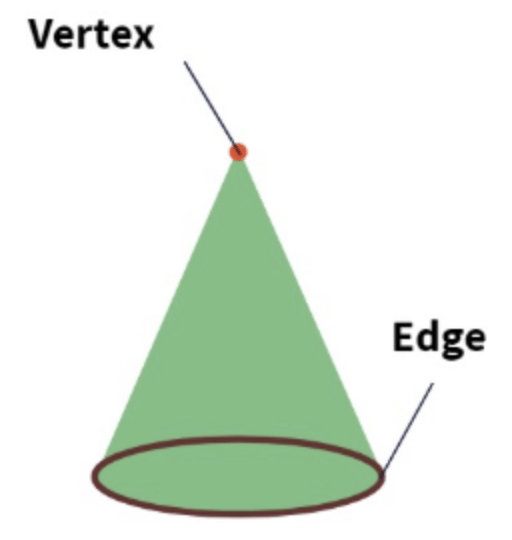
Parts of a Triangle:

• Sides: Triangles have three sides. Each side is a straight line that connects two corners.
• Corners (Vertices): Triangles have three corners where the sides meet. These corners are called vertices. Each vertex is where two sides come together.
  
  
• For Example: Slice of Pizza, Pyramid, Slice of watermelon

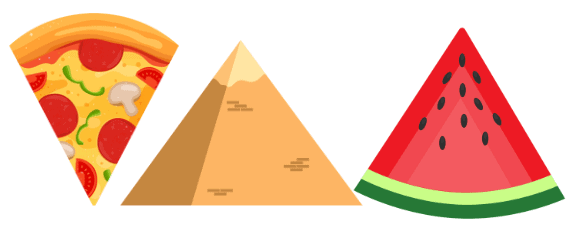
Triangles around us

Circle

Think of a circle as a round cookie. It’s a shape with no corners, and when you draw it, you start at one point and go all the way around until you return to the start.

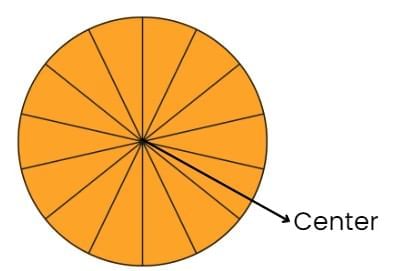
• Centre of a circle: The centre of a circle is the dot in the middle that is the same distance from every point on the edge of the circle.

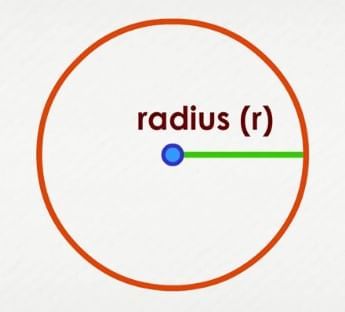
• Radius of Circle: If you draw lines from the centre to the edge, they will all be equal in length. This distance is known as the radius.
  
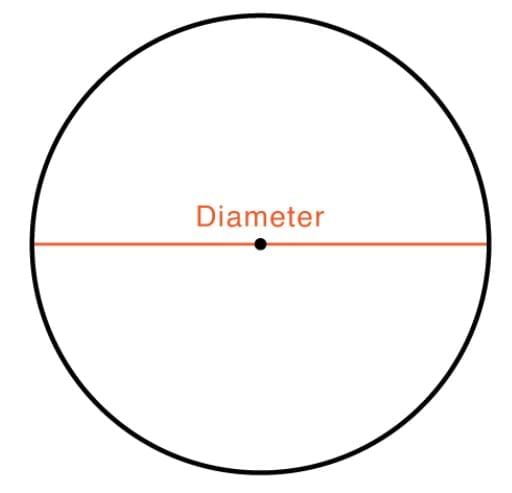
• The diameter is two times the radius and is the longest line that passes through the centre. 
  
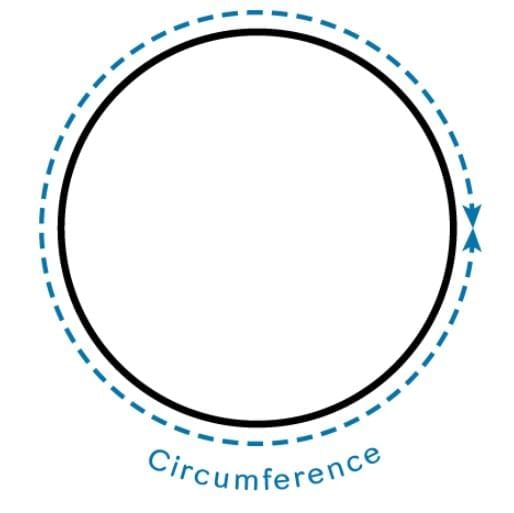
• The total distance around the circle is called the circumference.
  

Try yourself:

What is a shape with three sides and three corners called?

• A.Rectangle
• B.Circle
• C.Square
• D.Triangle

View Solution

Combination of Shapes

We can make all sorts of things by combining different shapes creatively. Here are a few examples:

1. House: A house can be made using rectangles for the walls, a triangle for the roof, squares or rectangles for windows, and circles for doorknobs or windows.

2. Car: A car might have rectangles for the body, circles for wheels, and triangles for headlights or the hood.

3. Tree: A tree can be made using a rectangle for the trunk, circles for leaves, and triangles for branches.

4. Robot: A robot could have rectangles for the body and limbs, circles for eyes or buttons, and triangles for decorations or parts of its design

5. Rocket: A rocket might use cylinders for the body, cones for the top or nose, rectangles for fins, and circles for windows or portholes.

By combining shapes in different ways, we can create all sorts of objects, from everyday things like houses and cars to imaginative creations like robots and rockets! It’s like putting together pieces of a puzzle to build something new and exciting.

How Do We Draw Shapes?

Take a pencil and paper—let’s make some shapes! There are two kinds of lines you can draw:

Two Main Types of Lines

• Straight lines are like the edges of a square or a rectangle. They don’t bend or curve; they just go straight from one point to another.
• Curved lines are like the edges of a circle or an oval. They bend and are not straight. They can be round or stretched out like an oval.

Try yourself:

What type of lines are like the edges of a circle or an oval?

• A.Straight lines
• B.Curved lines
• C.Dotted lines
• D.Wavy lines

View Solution

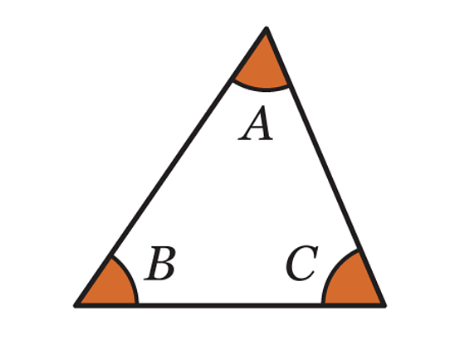
Shapes can also have different angles, which are important for classifying them. For example:

• A triangle has three angles.
• A rectangle has four right angles.

When you combine straight and curved lines in various ways, you can create all sorts of shapes like triangles, circles, squares, and rectangles. It’s like using building blocks to create different structures!

Introduction

Today, let’s explore how we add and take away numbers, and why these are super useful.

Addition is like putting things together. Imagine you have a pile of marbles. If you add more marbles to that pile, you end up with a bigger pile. For example, if you have 3 marbles and you add 2 more marbles, you will have 3 + 2 = 5 marbles in total.

Subtraction is like taking things away. Let’s go back to our marbles. If you have 5 marbles and you take away 2 marbles, you will have 5 – 2 = 3 marbles left.

So, addition makes things bigger by adding more, and subtraction makes things smaller by taking away. They’re like the opposite of each other!

Try yourself:

What does addition do to a number?

• A.Makes it smaller
• B.Makes it bigger
• C.Keeps it the same
• D.None of the above

View Solution

Learn with Story- Addition & Subtraction

Once upon a time, there were two kids named Suman and Aditya. They had six plant seeds that they wanted to plant in their garden. So, they decided to ask their grandpa for help. 

• Grandpa was very happy to see the kids doing something good, so he gave them four more seeds. 
• This is like adding because now they had 6 + 4 = 10 seeds in total.
• Excitedly, Suman and Aditya went to their garden. 
• They first planted two seeds next to the mango tree. 
• Now, they had 10 – 2 = 8 seeds left. 
• Then, they planted four seeds near the flowers. 
• Subtracting these, they had 8 – 4 = 4 seeds left. 
• Finally, they planted the remaining four seeds near the lemon tree. 
• This left them with 4 – 4 = 0 seeds, which meant they had used up all their seeds.

The kids were so happy to see their garden full of newly planted seeds, all thanks to their teamwork and Grandpa’s help!

Try yourself:What is the result of adding 7 and 5?

• A.12
• B.11
• C.13
• D.14

View Solution

Tens Frame

A tens frame is a simple math tool used to understand numbers in groups of ten. It consists of a rectangular frame with ten boxes or squares arranged in rows of five. Each box can hold one object, like a counter or a dot.

Addition using Tens Frame

Let’s say you have a tens frame with 6 counters placed in it. 

• This means that 6 out of the 10 boxes are filled, and there are 4 empty boxes.
• Now, if you add 4 more counters to the tens frame, you’ll fill up the remaining 4 empty boxes. 
• Counting all the counters, you’ll find that there are now 6 + 4 = 10 counters in total, filling the entire tens frame.

Subtraction using Tens Frame

Starting with a full tens frame of 10 counters, each box containing one counter, if you take away 2 counters, you’ll remove them from the filled boxes. 

• Now, you’ll have 8 counters remaining, filling 8 out of the 10 boxes on the tens frame.
• Continuing with subtraction, if you take away 4 more counters, you’ll remove them from the filled boxes. Now, you’ll have 4 counters remaining, filling only 4 out of the 10 boxes on the tens frame.
• Finally, if you take away the last 4 counters, you’ll remove them from the filled boxes, leaving the tens frame completely empty with 0 counters.
• Using the tens frame helps us see how adding fills up spaces, and subtracting takes away from those filled spaces, making it easier to understand addition and subtraction with numbers.

Try yourself:

In a tens frame with 8 counters placed, how many more counters are needed to fill it completely?

• A.2 counters
• B.10 counters
• C.5 counters
• D.3 counters

View Solution

Learn with Story- Using Number Line

Once upon a time, two kids named Maya and Arjun were sitting together, trying to solve a math problem that involved adding numbers bigger than 10. 

• They had a tens frame in front of them, which they were using to understand smaller numbers easily. 
• However, when it came to bigger numbers like 24 + 32, they started feeling confused.
• Just then, their elder brother Rahul walked into the room. 
• Seeing their puzzled faces, Rahul asked what they were working on. 
• Maya and Arjun explained that they were trying to add 24 and 32 using the tens frame but were finding it difficult.
• Rahul smiled and said, “Let me show you an easier way to do this using a number line.” 
• He drew a long line on a piece of paper and marked 24 on it. 
• “First, we start with 24,” Rahul explained. “Now, to make it easier, let’s add 6 steps to reach 30.” He marked 30 on the number line.
• “Next,” Rahul continued, “we add 10 more steps to reach 40.” 
• He marked 40 on the number line. “Then, another 10 steps to reach 50,” he added, marking 50 on the line. 
• “Finally, we add the remaining 8 steps to reach 58, which is our answer.”
• Maya and Arjun looked amazed. 

They could visually see each step of adding, making the process less confusing and more enjoyable.

Using number lines makes calculations easy because it breaks down the process into smaller, manageable steps that are visually represented. This helps in understanding the concept of addition or subtraction by visually seeing the progression of numbers, making it less daunting and more intuitive for learners.

Now, let’s help Arjun and Maya in subtracting 22 from 54 using the same method of the number line:

1. Start with 54 on the number line.
2. Subtract 10 to reach 44.
3. Subtract 10 more to reach 34.
4. Subtract 2 more to reach 32.

So, 54 – 22 = 32.

From that day on, Maya, Arjun, and Rahul always used the number line for bigger calculations, finding it to be a helpful and fun way to solve math problems.

Try yourself:

What is the missing number in the grid below?

Grid:
1 4 ?
2 5 8
3 6 9

• A.7
• B.10
• C.11
• D.12

View Solution

Number Grid

A number grid is like a map of numbers arranged in rows and columns. It’s similar to the grid used in games like Snake and Ladders, where each square in the grid contains a number. 

For example, a number grid from 1 to 100 would have 10 rows and 10 columns, with numbers ranging from 1 to 100 distributed across the grid.

• Using a number grid can help us visualize and understand mathematical operations like addition, subtraction, and movement in a structured way. Let’s take the example you mentioned:
• If we start at 8 on the number grid and move 2 steps up, we land on 28. This is because each step up in the grid adds 10 to the number. So, from 8, going up 2 steps means adding 10 twice (8 + 10 + 10 = 28).
• Similarly, if we start at 28 and move 2 steps to the right, we land on 30. This is because each step to the right adds 1 to the number. So, from 28, moving right 2 steps means adding 1 twice (28 + 1 + 1 = 30).
• Conversely, if we move to the left, each step subtracts 1 from the number. For example, if we start at 30 and move 2 steps to the left, we land on 28 (30 – 1 – 1 = 28).

In this way, a number grid helps us visualize and perform calculations by understanding the patterns of addition and subtraction associated with movement in different directions on the grid. It’s a useful tool for learning and practicing mathematical operations in a structured and interactive manner.

Solving Puzzle- Magic Sum

Imagine you have a 3×3 grid, like a small square divided into 3 rows and 3 columns. Each box in the grid has a number in it, but some boxes are blank. You also know the total sum for each row and column.

Let’s solve it step by step:

Horizontal Sum

1. First row: The given sum is 15, and you have 2 and 8 already. Adding them gives 10, so the blank box should be 15 – 10 = 5.
2. Second row: The given sum is 10, and you have 3 already. Subtracting 3 from 10 gives 7 for the first blank box. Then, the second blank box must be 0 to make the sum correct.
3. Third row: The given sum is 20, and you have 4 already. Subtracting 4 from 20 gives 16 for the first blank box. Then, the second blank box must be 0.

Vertical Sum

1. First column: The given sum is 17, and you have 3 already. Subtracting 3 from 17 gives 14 for the first blank box. Then, the second blank box must be 0.
2. Second column: The given sum is 7, and you have 2 already. Subtracting 2 from 7 gives 5 for the blank box.
3. Third column: The given sum is 21, and you have 7 already. Subtracting 7 from 21 gives 14 for the first blank box. Then, the second blank box must be 0.

So, the completed grid looks like this:

Now that we’ve learned how to add, subtract, and solve grid puzzles with bigger numbers, let’s keep practicing getting even better at math!

Try yourself:

What is the result of 37 – 15?

• A.22
• B.20
• C.18
• D.14

View Solution

Bundle

• A bundle is a group or collection of items put together.
• In mathematics, we often make bundles to count more easily.
• A common example is bundling 10 sticks.
• Together to form one group or bundle of 10.

Why Do We Use Bundles?

• Helps in counting large numbers.
• Easy to count when we group things in bundles, especially in tens.
• It helps in understanding place value(tens and ones).

Example:

Suppose you have 14 pencils.

• First, make a bundle of 10 pencils.
• Then, you will have 1 bundle of 10 pencils and 4 loose pencils left.
• So, 14 pencils = 1 bundle of 10 + 4 pencils.

Counting in 10s:
10, 20, 30, 40, 50, 60, 70, 80, 90, 100. 

Example: You have 10 apples in a basket. If Nani Maa adds 10 more apples each time, how many apples will you have after counting by 10s?

• Start with 10 apples.
• Add 10 more to get 20 apples.
• Add 10 more to get 30 apples.

Let’s do Addition to find total number of sticks:

                                                                                                           85 sticks + 67 sticks =  Total 152 sticks

Nisha and Nandni both collected sticks. Who collected more Nisha or Nandni? How much more?

Total no of Nisha’s stick = 85
Total no of Nandni’s stick = 67    

       85 sticks – 67 sticks =  18 sticks

       Nisha collected 18 sticks more than Nandni.

Try yourself:Raju sold 45 books on Monday and 68 books on Tuesday. How many books did he sell in two days?

• A.103 books
• B.113 books
• C.120 books
• D.23 books

View Solution

We practiced our math skills while playing games and enjoyed every moment with our family. Nani’s house was a special place where numbers and fun came together, making each day an exciting new lesson.

Until next time, keep counting, keep learning, and remember that every day can be an exciting new math adventure!

Chapter notes

A long time ago, people did not have number symbols like we do today. Instead, they made little marks on cave walls and tree bark to count things. Now, we use just ten digits—0, 1, 2, 3, 4, 5, 6, 7, 8, and 9—to write any number, big or small. Let’s see how this amazing system works!Ancient Methods of Counting

Counting with Groups

• Long ago, people counted things by grouping them into 5s, 10s, 20s, or even 60s. This made it easier to keep track of their things and trade with others.
• Thousands of years ago, ancient Indians created a special system using just ten digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. This was one of the greatest inventions in history!
  
• Thanks to this number system, we now have TVs, computers, mobile phones, and many other technologies!

The Importance of Zero

• A long time ago, people had no way to write “nothing.” Then, they invented zero (0)!
• This small number made a big difference! It helped make counting and math easier. Because of zero, we can do big calculations and solve tricky problems.

Now, this number system is used all over the world!

Sachin’s 99→100 SurpriseOne day, Sachin’s homework was to add 1 to every number:

• 1 + 1 = 2
• 2 + 1 = 3
• 23 + 1 =24
• 56 + 1 = 57
• … he kept going until he saw 99 + 1 = ?

Sachin scratched his head.
Just then his brother Vivek popped in.

Vivek: “What’s up, Sachin?”
Sachin: “I’m stuck at 99—what comes next?”
Vivek: “Easy—100!”

Sachin’s eyes lit up: “Oh—I get it now! 99 + 1 is 100!”

Vivek (smiling): “Numbers keep going forever. There’s always more to learn!”

Making 100

In math, we can make 100 in different ways by adding two numbers together. Let’s look at some examples:

• 90 + 10 = 100
• 80 + 20 = 100
• 70 + 30 = 100
• 60 + 40 = 100
• 50 + 50 = 100

This means there are many ways to make 100.

Using Matchsticks to Make 100

We can also use matchsticks to understand numbers.

If we take 10 bundles of matchsticks, with 10 sticks in each bundle, we get 100 matchsticks in total.

Try this:

• Count 10 matchsticks and make a bundle.
• Keep making bundles until you have 100 matchsticks.
• How many bundles do you need? (Answer: 10)

You can also try this with seeds, beads, or buttons to practice counting and making 100 in different ways.

Try yourself:

What is the result of 75 + 25?

• A.95
• B.100
• C.110
• D.120

View Solution

Let’s Learn by Practicing

Tanya and Reema, two friends who loved math, found a fun game one day. Tanya had learned in class how to make 100 by adding different numbers together. She was excited to share it with Reema.  

Tanya & Reema

• Tanya excitedly explained, “We can write down any five numbers between 1 and 99. Then, I’ll add another number to yours to make it 100!”
• Reema smiled and wrote down her five numbers: 20, 35, 42, 68, and 75.
• Tanya smiled and said, “Let’s begin!” She took Reema’s first number, 20, and added 80 to it, making it 100. “20 + 80 = 100!”
• Next, she looked at 35, added 65, and said, “35 + 65 = 100!”
• They kept playing, mixing numbers in fun ways. Tanya added 58 to 42, 32 to 68, and 25 to 75, making each one equal 100.

Exploring Other Ways to Make 100

• Besides the combinations Tanya made, we can use matchstick bundles and a number line to visualise making 100 in various ways. For example, using 10 matchsticks for tens and 1 for units can help us understand reaching 100.
• We can also estimate the number of objects, like oranges or bangles, to see how they can be grouped to make 100. This estimation improves our understanding of quantities.
• Another fun game involves using claps, snaps, and pats to represent numbers. For example, one clap could mean 100, one snap could mean 10, and one pat could mean 1. This interactive game aids in visualising numbers and their combinations.
• Just like the combinations Tanya made, many other ways exist to make 100 using different numbers. Let’s keep exploring creative number combinations!

Counting After 100

After reaching 100, counting continues in a similar way. Here’s how it works:

1. Using Hundreds:

• 100 + 1 = 101 (One Hundred One)
• 100 + 2 = 102 (One Hundred Two)
• 100 + 3 = 103 (One Hundred Three)

2. Hundreds and Tens:

• 100 + 10 = 110 (One Hundred Ten)
• 100 + 20 = 120 (One Hundred Twenty)
• 100 + 30 = 130 (One Hundred Thirty)

3. Hundreds and Ones:

• 100 + 5 = 105 (One Hundred Five)
• 100 + 8 = 108 (One Hundred Eight)
• 100 + 15 = 115 (One Hundred Fifteen)

To express numbers beyond 100, we use ten symbols (0-9) which help us write all numbers, where each place value (hundreds, tens, ones) is important in forming these numbers.

Try yourself:

What comes after 99 when counting?

• A.98
• B.100
• C.97
• D.101

View Solution

Number NamesUnderstanding Numbers Beyond 100

• Just as numbers below 100 have names, numbers above 100 do too.
• We will look at how these number names are structured.

Understanding 100

• Are these 100? 
  Yes, 10 bundles of 10 sticks make one bundle of 100.

Let’s Learn Names!

Once upon a time, there was a boy named Rahul who loved to learn new things. One day, he wanted to learn the names of numbers above 100, but he found it a bit difficult. He struggled to say numbers like 101, 105, or 110.

Names of Numbers Above 100

Rahul & Anju

• Rahul felt a bit frustrated, but then his older sister Anju noticed his confusion. Anju was great at explaining things simply.
• Anju sat down with Rahul and said, “Let me show you how to name numbers above 100, Rahul. It’s easy!”
• She started with 100 and explained, “When we have 100 and add 1, it becomes One Hundred One. We just say ‘One Hundred’ and then add the next number.”
• Rahul’s eyes lit up with understanding. “Oh, so 100 and 2 is One Hundred Two, right?”
• Anju nodded, “Exactly! You’re getting it.”
• Next, she showed him 100 and 5, saying, “When we have 100 and add 5, it’s One Hundred Five.
• Then she explained, “100 and 9 make One Hundred Nine. “
• Finally, she said, “And 100 and 10 makes One Hundred Ten.”

Examples

• 109 – One Hundred Nine
• 123 – One Hundred Twenty Three
• 150 – One Hundred Fifty
• 157 – One Hundred Fifty Seven
• 159 – One Hundred Fifty Nine

Explanation

• 109 – Here we have a Hundred and a Nine, so its name will be One Hundred Nine.
• 123 – One Hundred + Twenty Three = One Hundred Twenty Three
• 150 – One Hundred + Fifty = One Hundred Fifty
• 157 – One Hundred + Fifty Seven = One Hundred Fifty Seven
• 159 – One Hundred + Fifty Nine = One Hundred Fifty Nine

From that day on, Rahul was confident in naming numbers above 100, thanks to his sister’s clear explanations and patient teaching.

Try yourself:

What is the number name for 145?

• A.One Hundred Forty Five
• B.One Hundred Fifty Four
• C.One Hundred Forty Six
• D.One Hundred Forty Seven

View Solution

Let’s Learn Combinations!

Once upon a time, there was a clever little dog named Bingo. Bingo loved playing with numbers. One day, he decided to help his friends learn how to add numbers to reach a target by inviting them to a fun game.

Bingo said, “Just like Bingo and his friends, you can also try more examples to understand how numbers work. Our first goal is to make 100.”

Bingo pointed to the number line and asked, “If we start with 50, what can we add to make 100?” His friends thought for a moment and shouted, “50! Because 50 + 50 equals 100!” Bingo wagged his tail happily.

Bingo continued, “How about making 200?” One friend replied, “We can add 140 and 60 because 140 + 60 equals 200!” Bingo smiled and explained, “You could also add 150 and 50 or 120 and 80. See how many ways we can reach our goal?”

Exploring Combinations

• 60 and 40 make 100
• 45 and 55 make 100

Bingo clapped his paws and said, “Great job, everyone! You’ve learned to add numbers to make bigger numbers!”

Now, let us play a game called “Clap, Snap, and Pat.” One clap represents 100, one snap represents 10, and one pat represents 1. You can play this game in teams where one team shows a number using claps, snaps, and pats, and the other team guesses it.

And so, Bingo and his friends kept playing with numbers, learning new ways to add and reaching their target goals. They had so much fun learning together!

Just like Bingo and his friends, you can also try some more examples and understand how numbers work.

Let’s Practice!

Question 1: 
Write numbers in the blank spaces inside the flower petals so that the numbers in each petal add up to 100.   View Answer

Question 2: 
Look at the picture. Estimate and write the number of each of the following objects.

a. Oranges: …………..

b. Bangles: ………….

c. Laddoos: …………

d. Barfi :……………

e. Bindis: ……………

f. Bananas: …………………


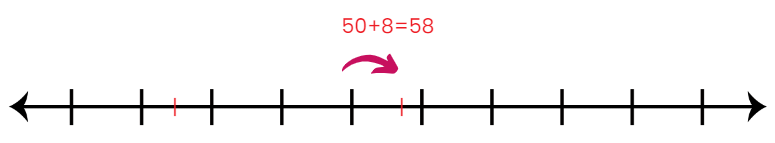
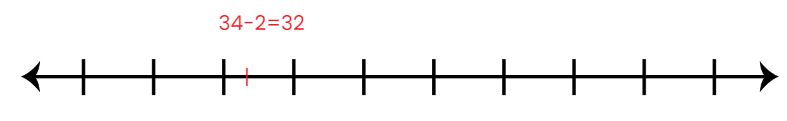
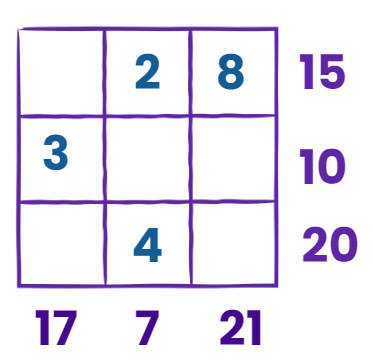
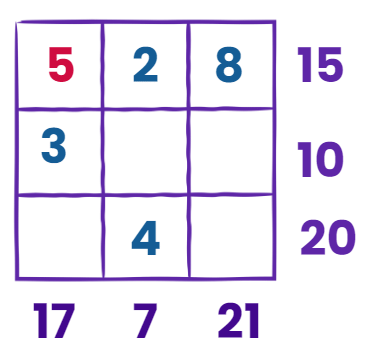
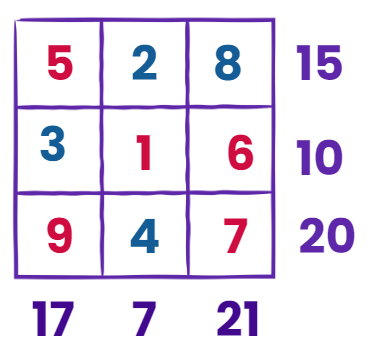
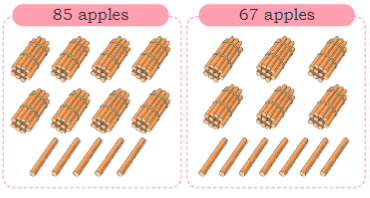
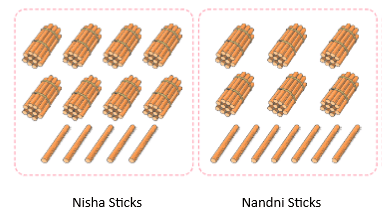
  View Answer

Introduction

Have you ever looked at your toys, snacks, or even the things around your house and wondered, “What shape is that?“

 Shapes are not just fun to look at—they are all around us, and some shapes are even 3D, meaning we can touch and hold them!

In this lesson, we’ll explore exciting shapes like cubes, cones, spheres, and cylinders. Let’s dive into the magical world of 3D shapes!
We will take a look at how they are identified and what are the common shapes present around us.

What are 3D Shapes?

These are shapes you can feel and hold; they are not just flat like a drawing on paper. Here are some examples:

• Cube: Think of a dice or a Rubik’s Cube. It’s a unique type of cuboid, like a solid box with six square sides.
• Sphere: Imagine a ball or an orange. It is entirely round, similar to a basketball.
• Cylinder: Picture a can of soda or a torch. It’s shaped like a tube with two circular ends.
• Cone: Think of an ice cream cone or a party hat. It resembles a triangle that narrows to a point.

Let’s take a look at some 3D shapes: 

Try yourself:

Which 3D shape can be compared to an ice cream cone or a party hat?

• A.Cube
• B.Sphere
• C.Cylinder
• D.Cone

View Solution

Now that we recognise the different 3D shapes, let’s explore more.Let’s Understand with a Story

Once upon a time, there lived a curious boy named Kunaal. He had just learned all about different 3D shapes in his school, and he was excited to share the new things he learnt with his little sister, Ayushi. Kunaal knew that learning about shapes could be so much fun, especially when you can see them all around you.

• One sunny afternoon, Kunaal called out to Ayushi, “Hey Ayushi, come with me! I want to show you something really cool.” Ayushi, always happy to learn from her big brother, quickly joined him.
• Kunaal took Ayushi on a tour around their house. “Look, Ayushi,” Kunaal said with a smile, “see that box of building blocks? It’s shaped like a cube!” 
• Next, they went to the kitchen, where Kunaal pointed at a cereal box. “This is a cuboid,” he explained. “It’s like a stretched-out cube with rectangular faces. See how it’s longer than it is wide?”  
• As they moved to the living room, Kunaal spotted a party hat from Ayushi’s recent birthday celebration. “Look at this cone,” he exclaimed. “It’s like a triangle that’s getting narrower as it goes up. Remember the ice cream cones we love?” 
• In the garden, Kunaal picked up a ball. “This is a sphere,” he said, rolling it in his hands. “It’s completely round, just like a basketball.” 
• Finally, they went to the garage, where Kunaal showed Ayushi a flashlight. “See this cylinder! It’s like a can of soda or a tube. It has two circular faces and a curved surface.” 
• Ayushi was amazed at how many shapes they could find right in their own home. “Thank you, Kunaal Bhaiya,” she said happily. “Now I understand 3D shapes, all thanks to you!” 

Kunaal was happy and proud to have shared his knowledge with his sister. From that day on, whenever they played or explored, Ayushi would point out different shapes.

More About 3D Shapes

Shapes have different parts. Let’s explore them:

• Face: In geometry, a face is a flat surface on a 3D shape. Think of it like the side of a box or a piece of paper. Faces are what you see when you look at a shape from different angles. For example, if you look at at a cuboid, each of its six sides is a face. Here we can take a look at face of a cuboid. 
• Edge: An edge is like a line where lines of two shapes meet. Imagine the edges of a cuboid—it’s the lines where the faces come together. Here we can take a look at edges of a cuboid (black line is the edge)
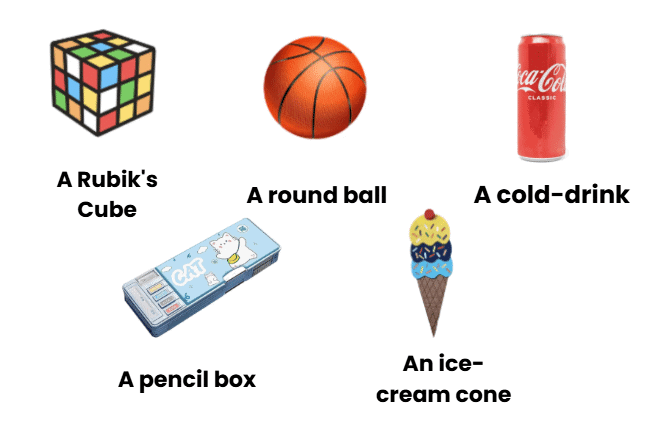
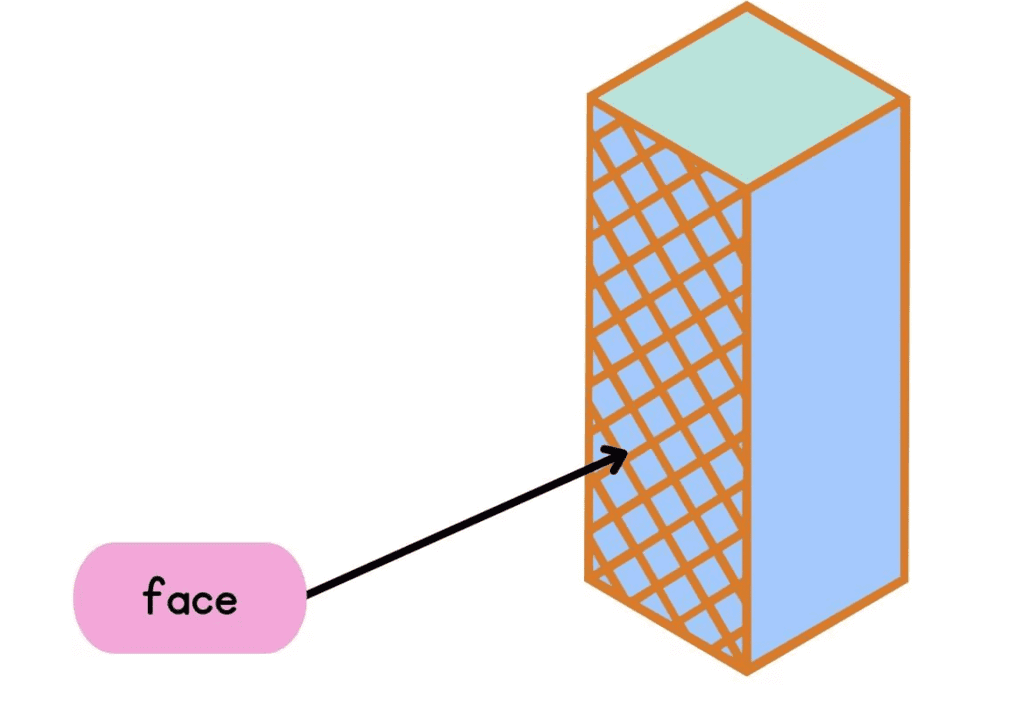
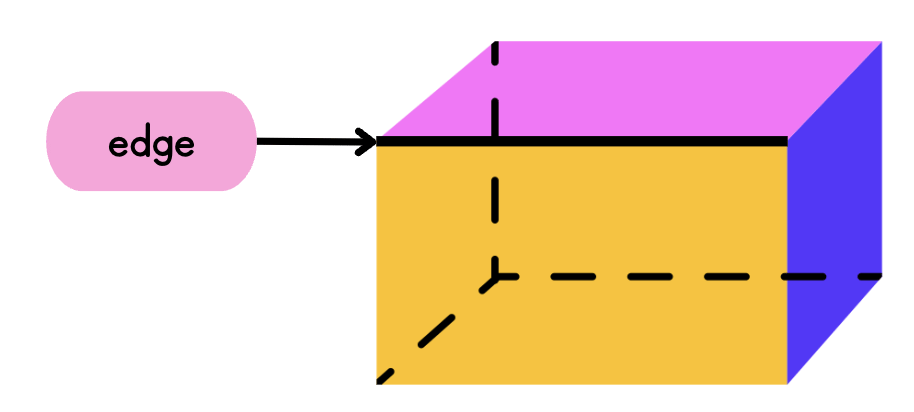
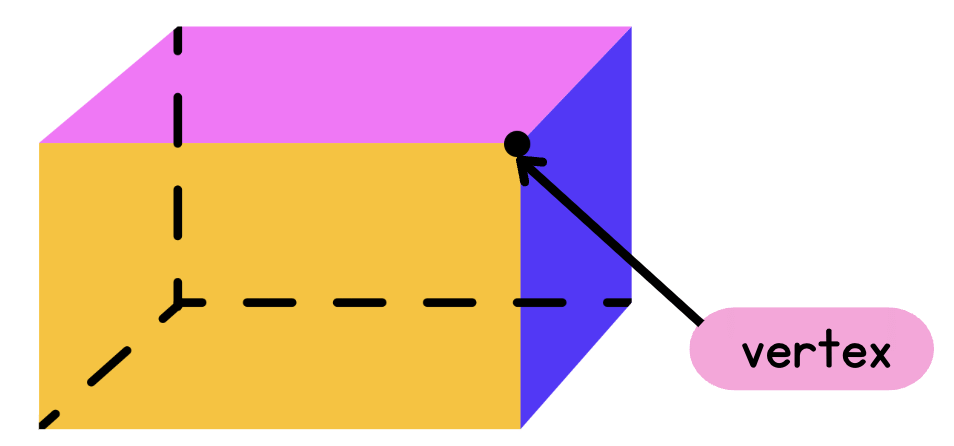• Corner (Vertex): A corner, also called a vertex, is a point where edges meet. It’s like the tip of a pyramid or the corner of a room. In a cube, each of its eight corners is where three edges meet. A vertex can also be defined as a point in space where two or more edges meet.Now we will study how shapes differ from each other.

Cube

• Faces: A cube has 6 square faces.
• Edges: A cube has 12 edges where two faces meet.
• Corners (Vertices): A cube has 8 corners where three edges join.
• Example: Dice (die) used in board games, rubik’s cube, sugar cubes, etc. 

Cuboid

• Faces: A cuboid has 6 faces, all of which are rectangles. If all sides are equal, it is specifically a cube, which is a special type of cuboid.
• Edges: A cuboid has 12 edges, similar to a cube.
• Corners (Vertices): A cuboid has 8 corners where three edges meet.
• Examples: Pencil Box, match-stick box, etc. 

Try yourself:

Which 3D shape has 6 square faces, 12 edges, and 8 corners?

• A.Sphere
• B.Cone
• C.Cube
• D.Cylinder

View SolutionCone

• Faces: A cone has two faces—a circular base and a curved surface that comes to a point at the top.
• Edges: It features one curved edge and one straight edge along the base.
• Corners (Vertices): There is one vertex at the top of the cone.
• Examples: Party hats, Ice-cream cones, etc.

Sphere

• Definition: A sphere is a perfectly round three-dimensional shape where every point on its surface is the same distance from its centre.
• Faces: A sphere has no flat faces.
• Edges: There are no edges on a sphere as it is smooth all around.
• Corners (Vertices): A sphere has no corners or vertices since it has no flat faces.
• Examples: Balls, bubbles, etc. 

Cylinder

• Faces: A cylinder has 2 circular faces and 1 curved surface.
• Edges: A cylinder has 2 edges—one around the circular top and one around the circular bottom, plus 1 curved edge along the side.
• Corners (Vertices): A cylinder has no corners (vertices).
• Examples: Rollers, cans, gas cylinders,etc. 

Let’s Practice!

Ques: Milin went to a shop and bought a toy engine.
Here’s his toy engine, count the shapes which are present in this toy-engine.

(i) Cylinder(s) ………………………………………..
(ii) Cone(s): …………………………………………..
(iii) Cuboid(s) ……………………………………….
(iv) Cube(s) ………………………………………….

Answer:
(i) Cylinder(s) : 1
(ii) Cone(s):2
(iii) Cuboid(s):1
(iv) Cube(s): 1

Introduction

Imagine you have a big jar of candies and you really want to know exactly how many are inside. What would you do?

That’s where counting comes in—a superpower that helps you keep track of everything!

Now, let’s meet two brothers who used counting in a very smart way.

A Cow Story: Deba and Deep Learn to Count

Long ago, in a village, two brothers named Deba and Deep looked after cows. Every day, they took the cows out for grazing and brought them back in the evening.

• One day, Deba asked, “How do we know if all cows have come back?”
• Their friend suggested, “Make a mark on the wall for each cow when it leaves. When it returns, strike the mark. If all marks are gone, all cows are back!”

• Next day, they tried it. And it worked! From that day, they always used counting marks to keep their cows safe.

Try yourself:What did Deba and Deep do to keep track of the cows?

• A.Follow them everywhere
• B.Make marks on the wall
• C.Use a bell
• D.Count them every hour

View Solution

What Happened Later?

• As years passed, Deba and Deep had more cows. One day, before leaving, they made marks on the wall for each cow. When they came back, they started striking out the marks as each cow entered the gate.

Marks on the wall that represent the number of cows

• But two marks were still left! And no cows were outside!
• Why were they worried? Because this meant two cows were missing!
• They quickly went to search and found the missing cows nearby. Thanks to their counting trick, they saved their cows.
• Counting saved the day!

Why Counting Is Important

• To Know How Many: Counting tells us how many toys, sweets, or books we have.
• To Share Fairly: You can count your candies to share them equally with your friends.
• To Solve Problems: Lost something? Count what you have to know what’s missing.
• To Make Plans: If your birthday is in 5 days, you can plan something for each day!

Let’s Count Letters in Names!Let’s take the name “Samantha”.

• Write it out: S-A-M-A-N-T-H-A
• Count each letter: That’s 8 letters!

Now try your own name. How many letters?

You can also:

• Find names that start with the same letter.
• Check which letter is used the most.
• Find the shortest and longest names in your class!

Try yourself:How many letters are there in the word “MATHEMATICS”?

• A.11
• B.5
• C.3
• D.4

View SolutionWho Has the Longer Name?

• Richa and Ayushi were sisters. One day, they argued.
  
• “My name is bigger!” said Richa. “No! Mine is!” replied Ayushi.
• Their brother Rahul said, “Let’s count the letters.”
  
  
• Richa: R-I-C-H-A = 5 letters
  
  Ayushi: A-Y-U-S-H-I = 6 letters
  
  
• Ayushi’s name was longer! They laughed and made up. Counting helped them solve the argument.

So, counting isn’t just about numbers. It’s a way to explore, learn, and solve problems, just like Richa and Ayushi did!

Counting in Number Names

Let’s try the number “Seven”.

• S-E-V-E-N = 5 letters
  Try with other numbers:

• Three = 5 letters
• Eleven = 6 letters
• Twenty = 6 letters

Number names are words for numbers. Instead of 1, we say “One”. 
Below are the number names for the first few natural numbers:

Let’s Practice with Number Friends!

In the land of Numerica, friends Eighty-Nine, Ninety, and Ninety-One wanted to see who had the longest name.
Let’s count the letters in their names to see who has the biggest name!

• “Eighty-Nine” = 10 letters
  
• “Ninety” = 6 letters
  
  
• “Ninety-One” = 9 letters
  

Eighty-Nine had the longest name! But they all learned counting and had fun together.

The friends celebrated their newfound knowledge and friendship, knowing that each of their names was special in its own way.

Just like this, we can count the letters in all the numbers’ names and other words as well. Keep practicing, and you’ll become a pro at counting letters in no time!