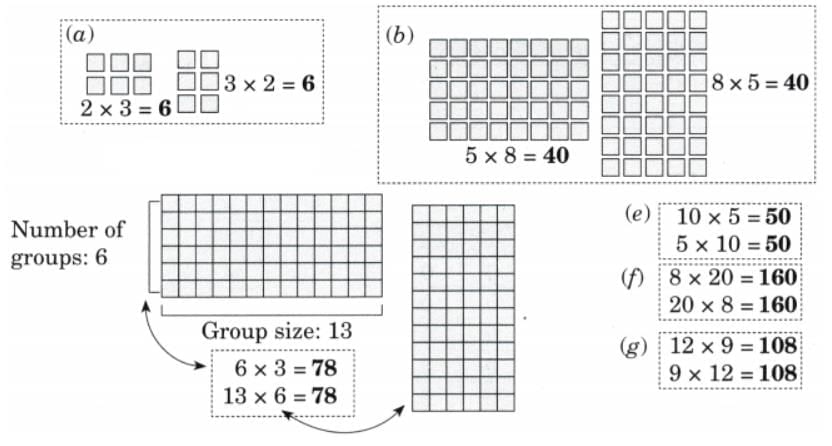
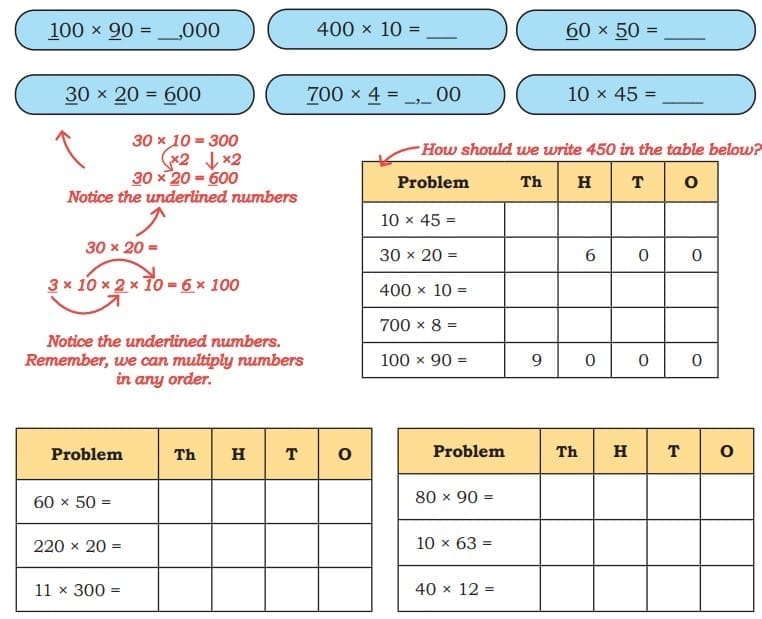
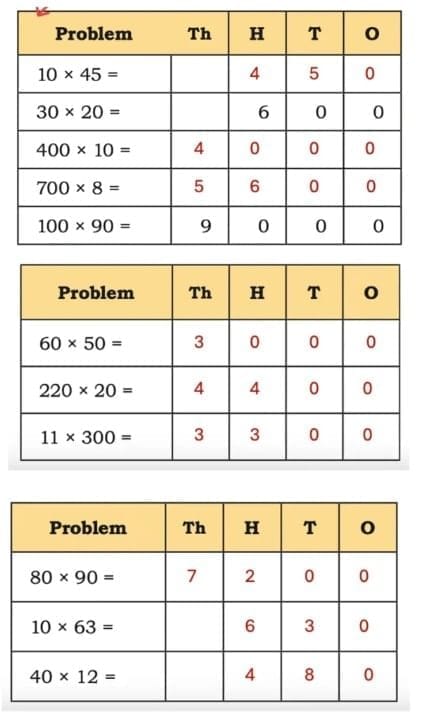
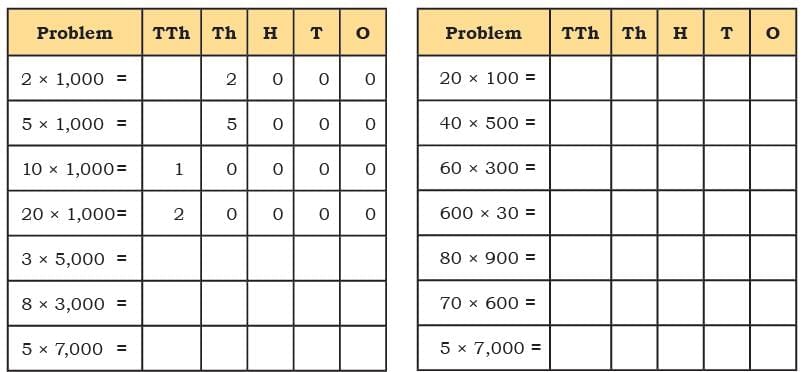
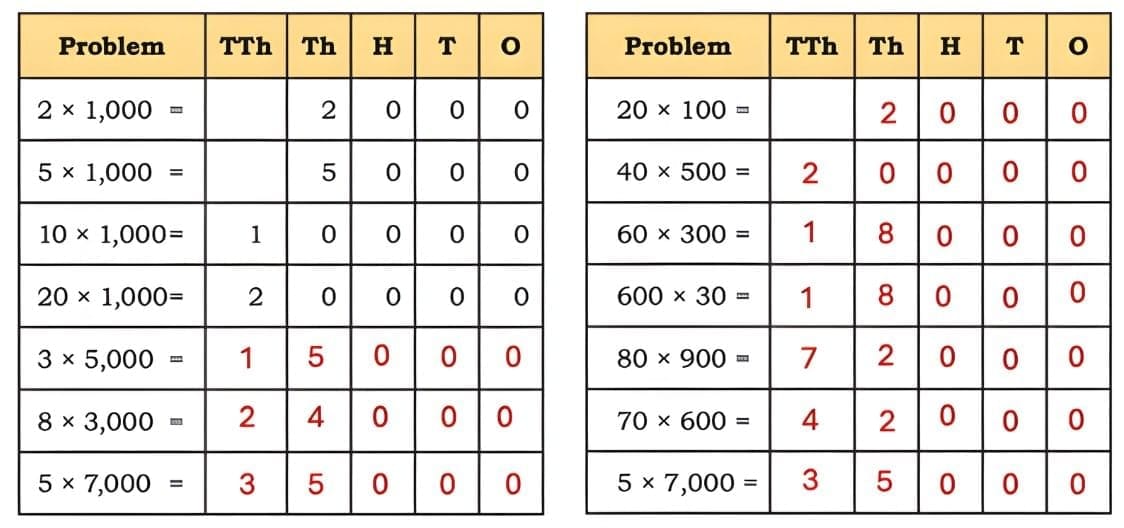
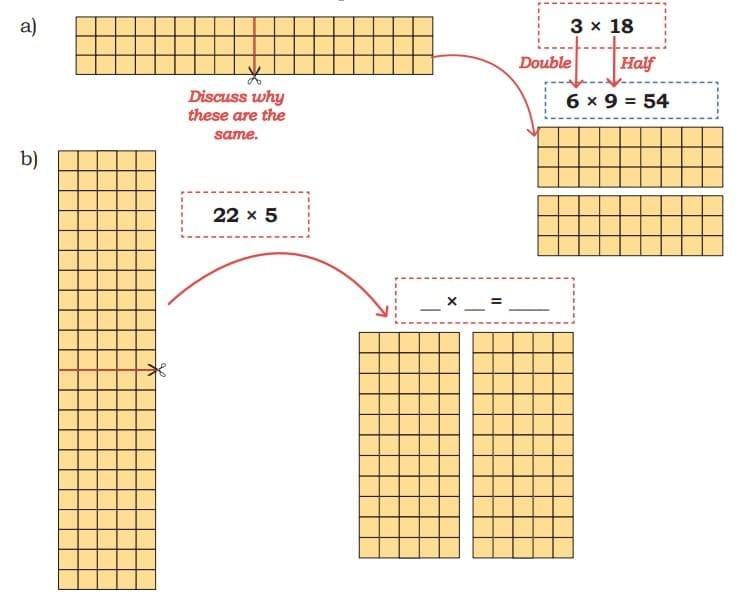
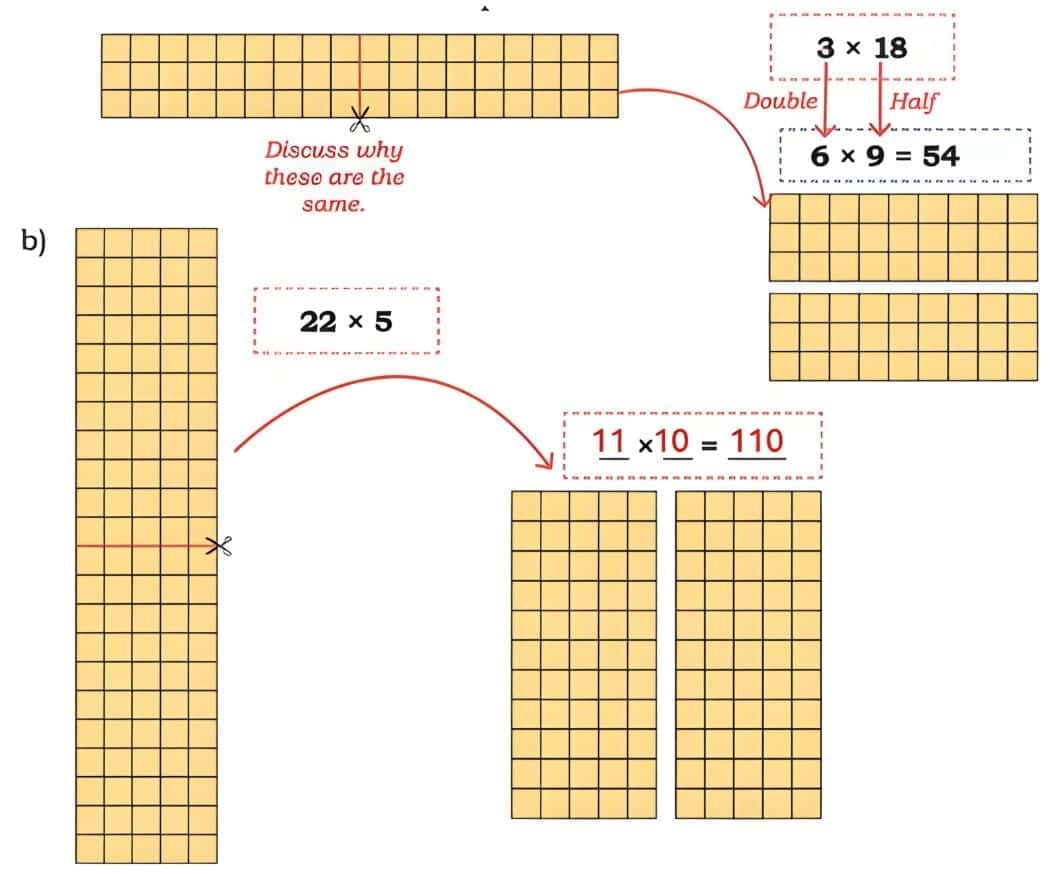
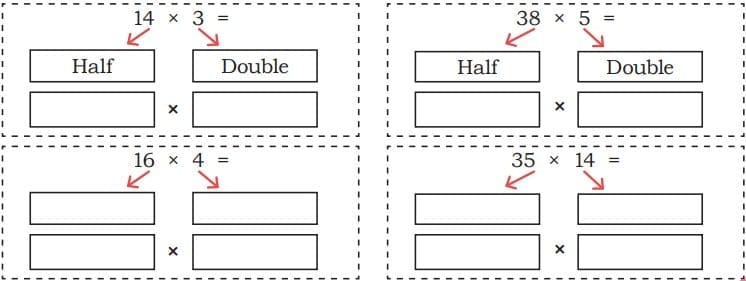
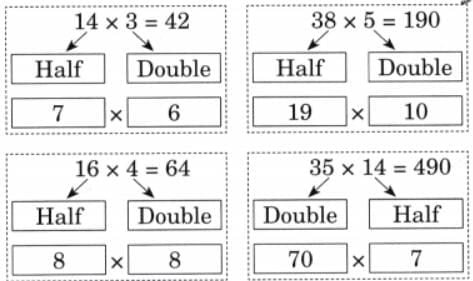
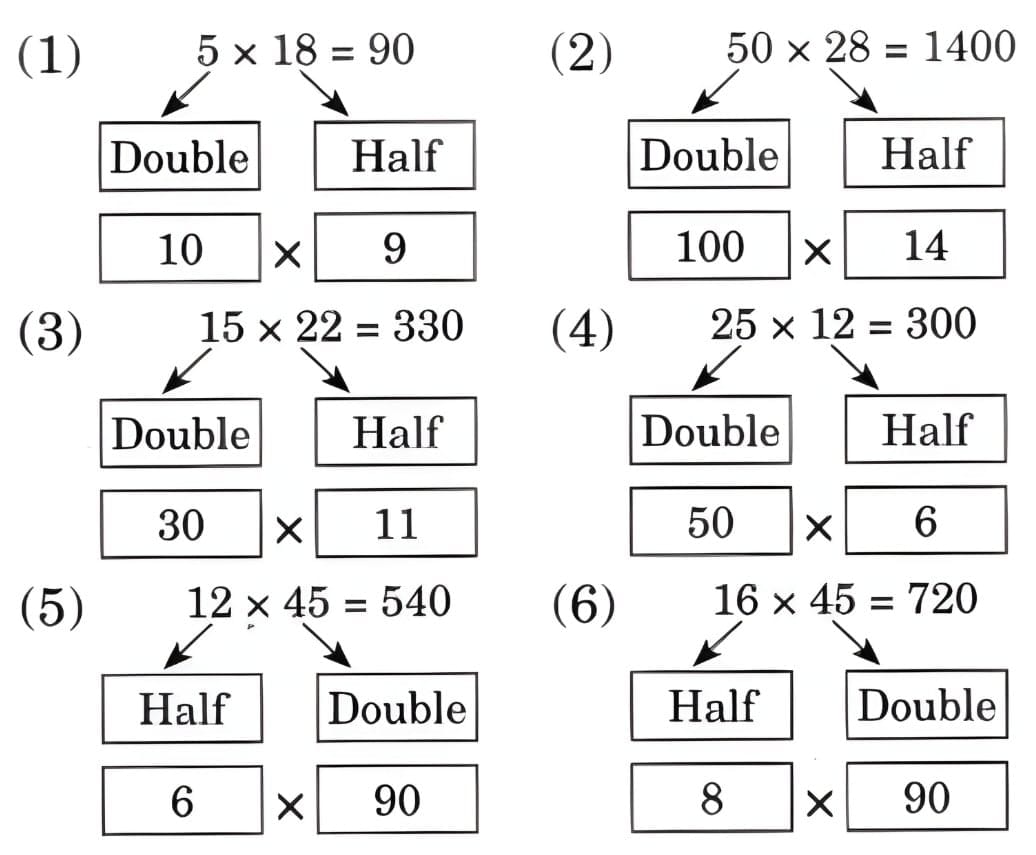
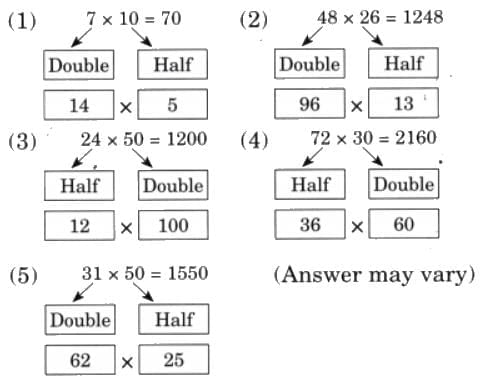
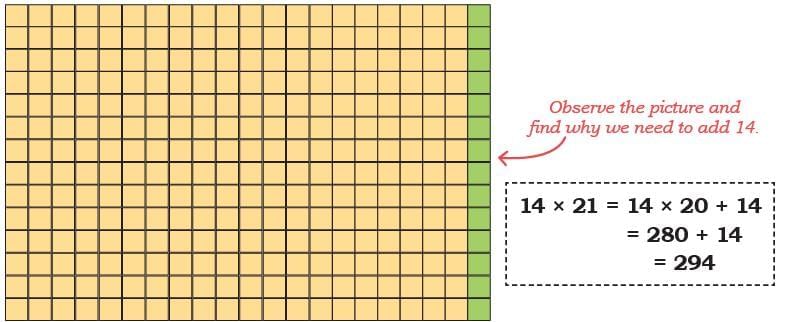
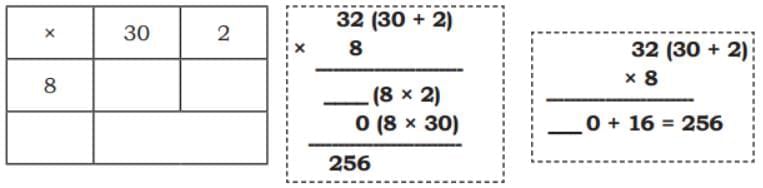
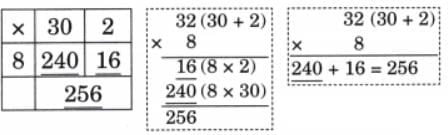
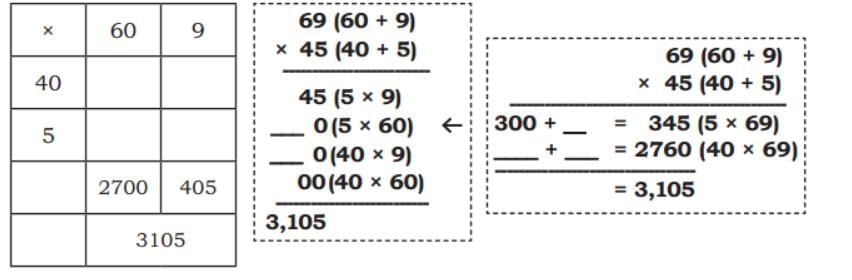
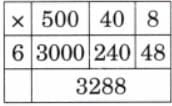
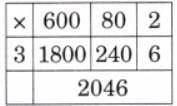
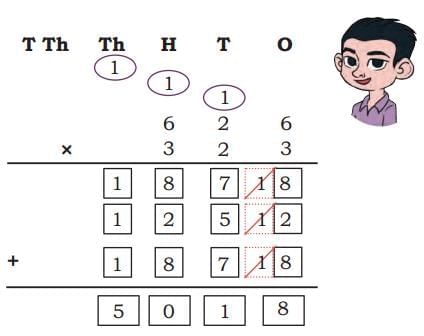
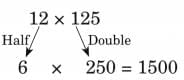
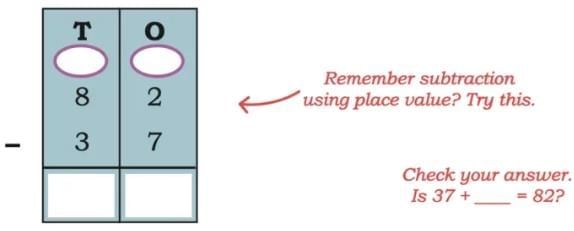
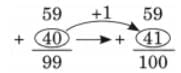
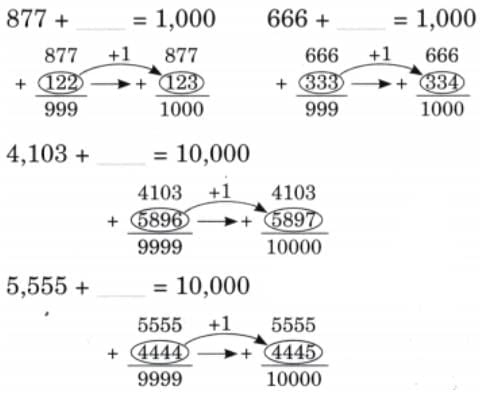
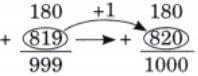
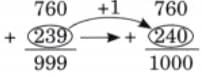
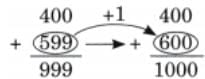
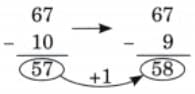
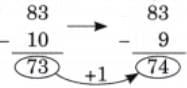
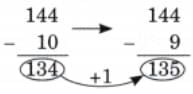
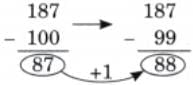
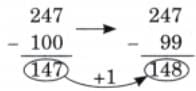
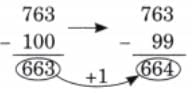
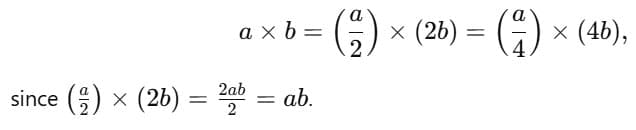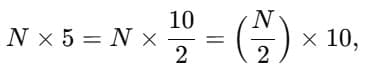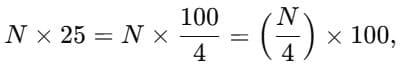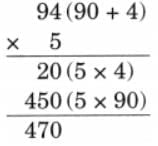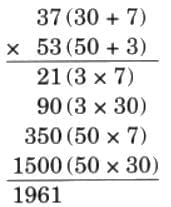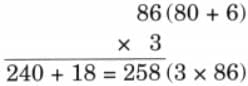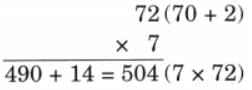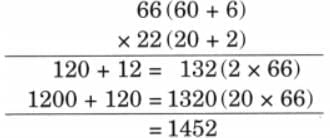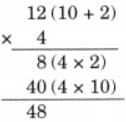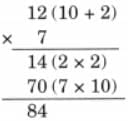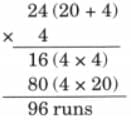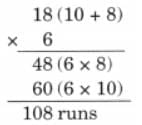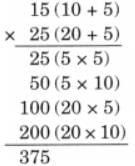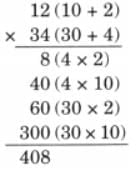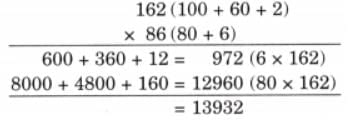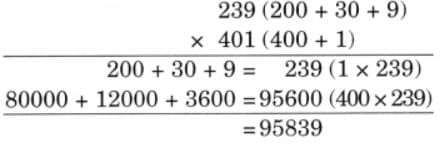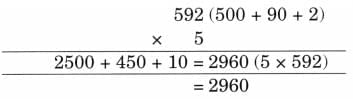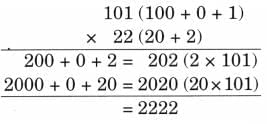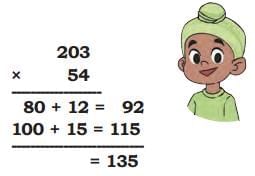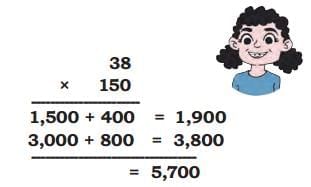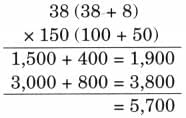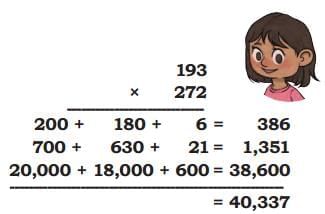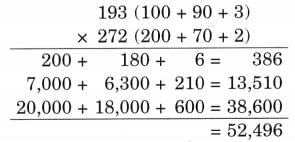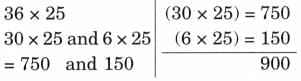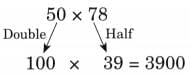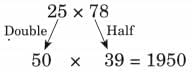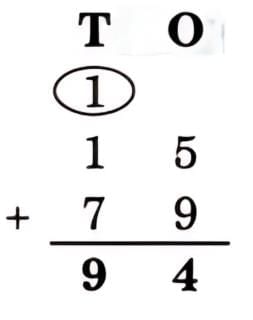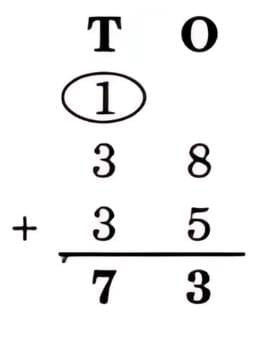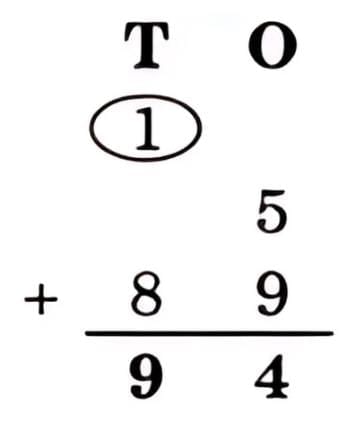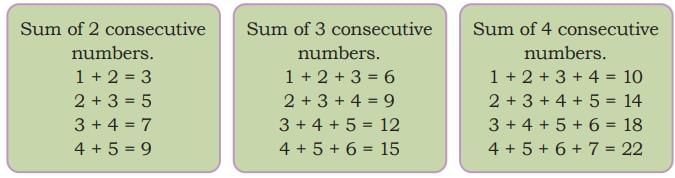Child TV Reporter
Samaira and Kabir decided to act like reporters and collect information from their friends.
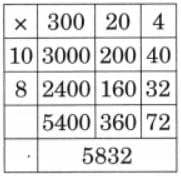
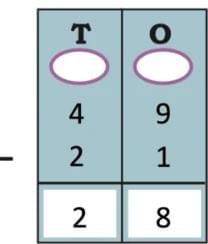
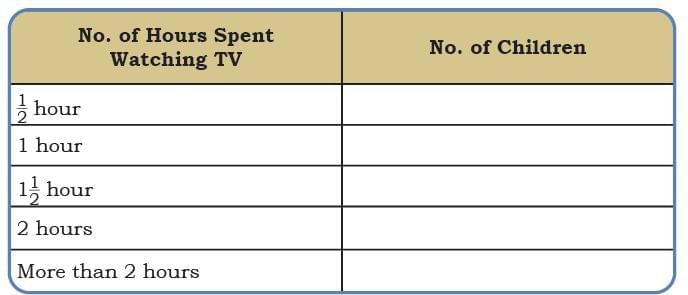
They collected data from 35 friends and recorded it in a notebook as shown below.
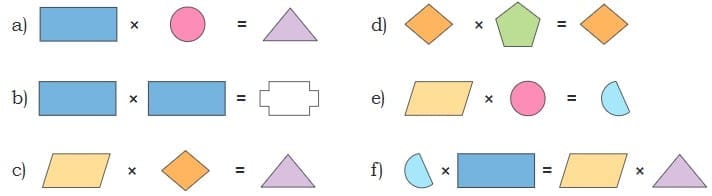
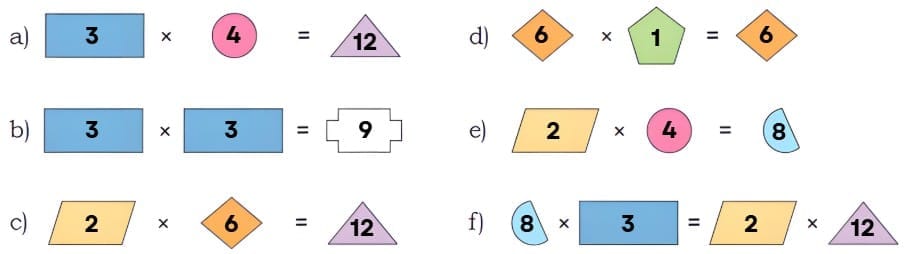
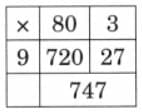
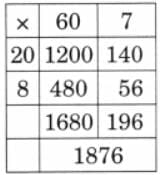
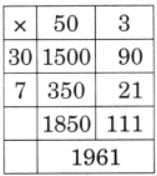
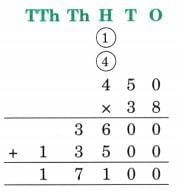
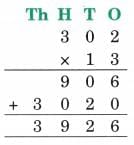
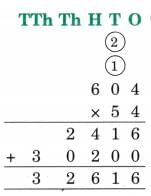
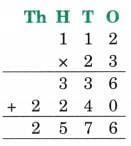
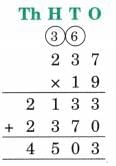
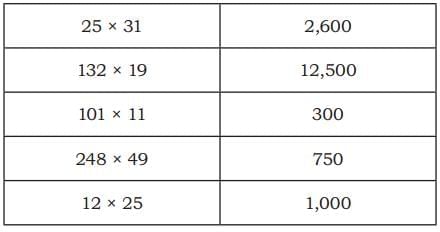
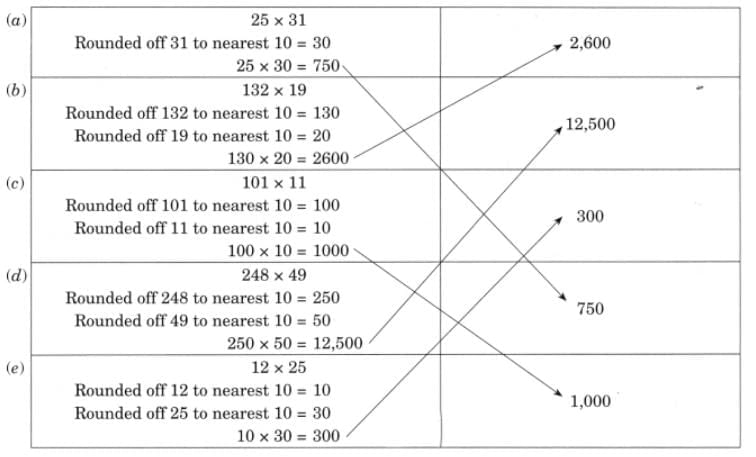
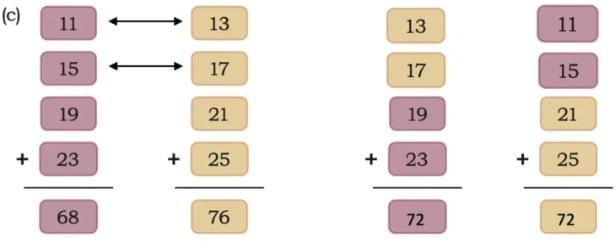
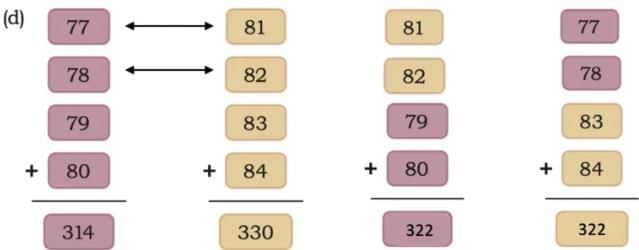
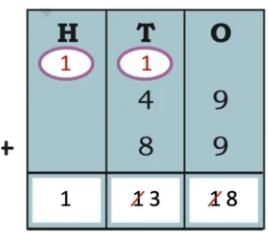
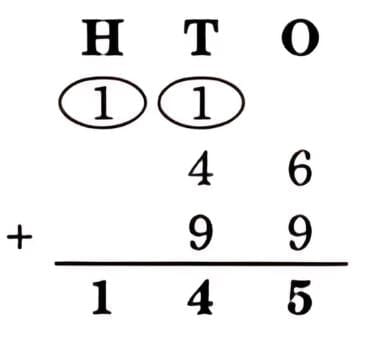
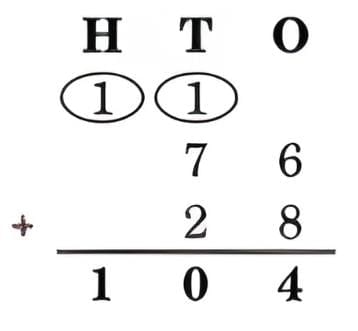
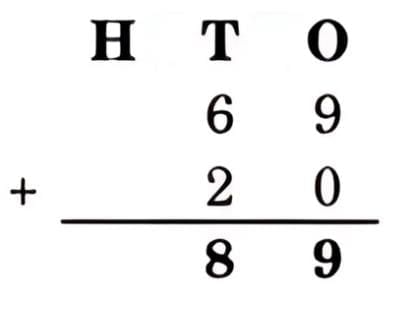
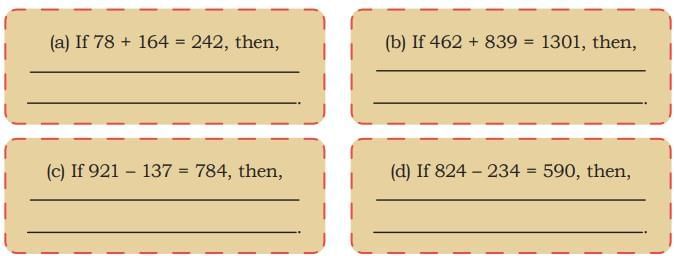
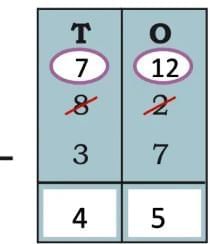
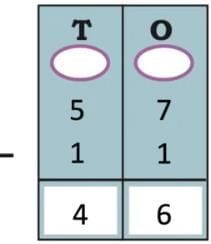
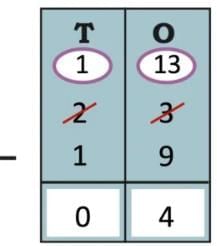
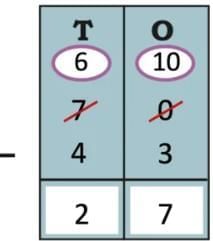
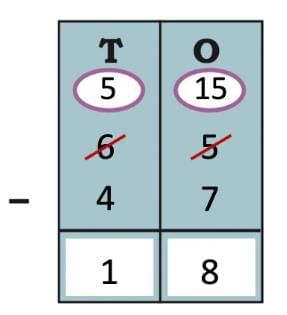
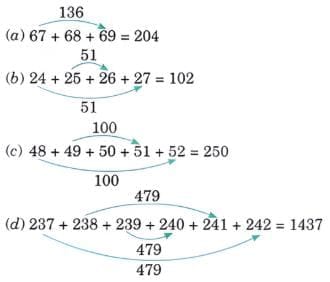
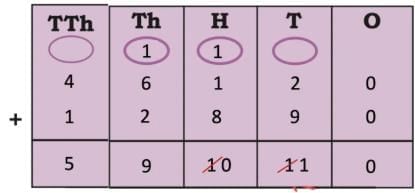
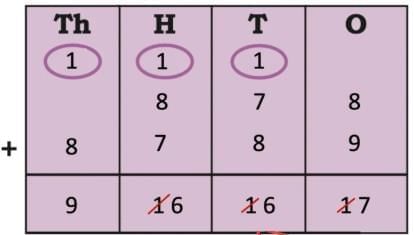
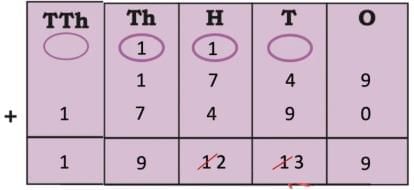
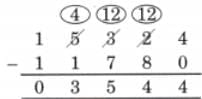
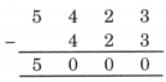
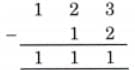
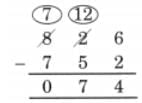
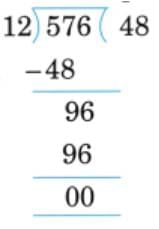
Ans:
Look at the table and answer the following questions.
Q1: How many children watch TV for more than half an hour?
Ans: Number of children who watch TV for more than half an hour =13 + 7 + 3 + 3 = 26 children.
Q2: How many children watch TV for less than two hours?
Ans: Number of children who watch TV for less than two hours = 9 + 13 + 7 = 29 children.
Q3: The number of children who watch TV for more than two hours is _________.
Ans: Number of children who watch TV for more than two hours is 3.
Q4: More children watch TV for two hours than half an hour. (True/False)
Ans: Given statement is false, since only 3 children watch TV for two hours, but 9 children watch TV for half an hour.
Yes, watching TV for too long can cause eye strain and tiredness.
Stock-Taking in a Shop
Joseph Uncle takes stock of the play items (toys, board games, and sports items) in his store a week before the summer break. He tries to record the items in his shop using a pictograph. He notices that there are too many items of each kind in his shop and it is not easy to make a picture for every item Dipesh, one of his helpers, suggested using one picture (icon) for every 5 items of each kind.
Dipesh, one of his helpers, suggested using one picture (icon) for every 5 items of each kind.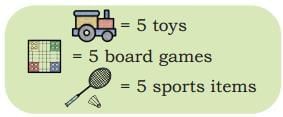 His pictograph is shown below.
His pictograph is shown below.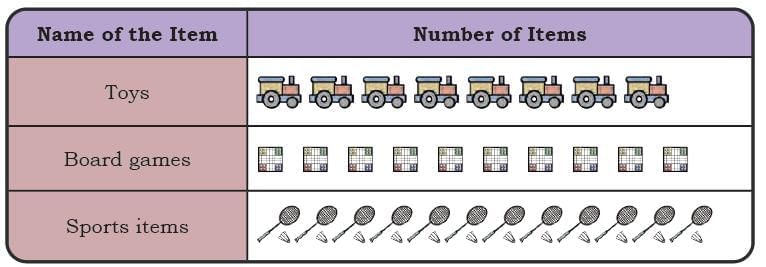 Dipesh used a scale while recording the items in the pictograph. A scale helps record a large number of things using fewer icons.
Dipesh used a scale while recording the items in the pictograph. A scale helps record a large number of things using fewer icons.
Now, answer the following questions based on the above pictograph.
Q1: How many toys does Joseph Uncle have?
Ans: Joseph Uncle has 8 × 5 = 40 toys
Q2: How many board games does Joseph Uncle have?
Ans: Joseph Uncle has 10 × 5 = 50 board games.
Q3: How many total play items does Joseph Uncle have?
Ans: Joseph Uncle has 12 × 5 = 60 sports items.
Thus, total play items Joseph Uncle has = 40 + 50 + 60 = 150.
Q: Is there any other scale that you can use to make the pictograph?
Ans: Yes, we can use another scale to make the pictograph simpler.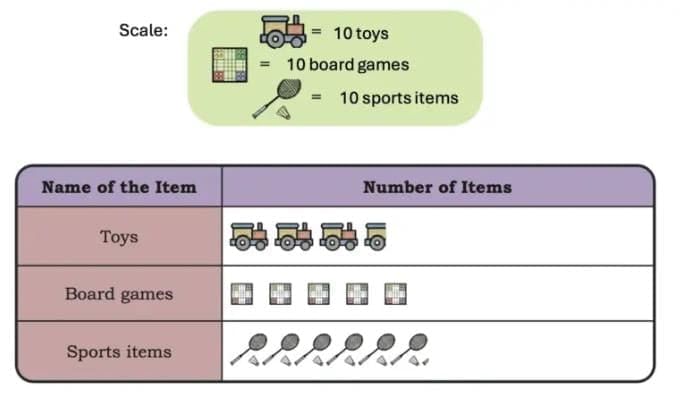
Two-wheelers on the Road
Deepti noted down the number of two-wheelers passing her house in one hour on three different days.
She used one icon to show 3 two-wheelers.
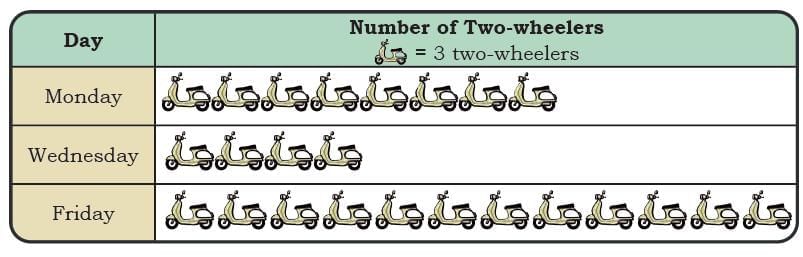
Observe the pictograph and answer the following questions.
Q1: Which day had the most two-wheelers passing her house?
Ans: Friday
Q2: How many total two-wheelers did she record over three days?
Ans: Two-wheeler recorded on Monday
= 8 × 3 = 24 two-wheelers
Two-wheeler recorded on Wednesday
= 4 × 3 = 12 two-wheelers
Two-wheeler recorded on Friday
= 12 × 3 = 36 two-wheelers
Total two-wheelers Deepti recorded over three days = 24 + 12 + 36 = 72 two-wheelers
Q3: How many fewer two-wheelers were seen on Wednesday than on Monday?
Ans: On Monday, Deepti saw 24 two-wheelers
On Wednesday, Deepti saw 12 two-wheelers
Difference = 24 – 12 = 12 two-wheelers
∴ 12 fewer two-wheelers were seen on Wednesday than on Monday.
Q4: How many more two-wheelers were seen on Friday than on Wednesday?
Ans:
On Wednesday, Deepti saw 12 two-wheelers.
On Friday, Deepti saw 36 two-wheelers.
Difference = 36 – 12 = 24 two-wheelers.
24 more two-wheelers were seen on Friday than on Wednesday.
Q5: Choose any other scale and represent the same data using a pictograph in your notebook.
Ans: Here 1 = 4 two-wheelers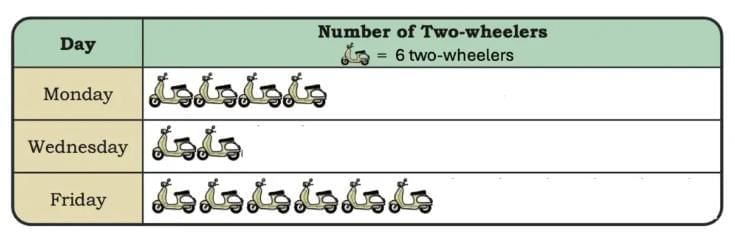
Recording a Day
One day Raman and Sheela decided to record how they spent their day.
Raman recorded his daily routine in the table below.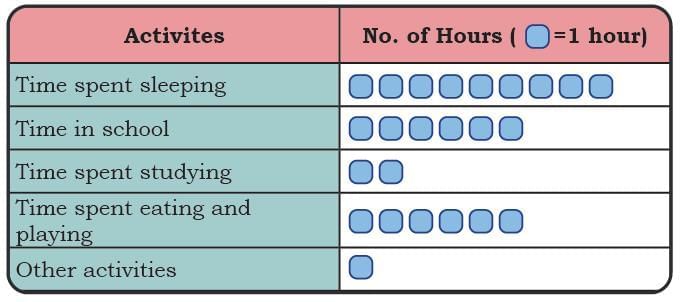 Sheela recorded her routine in the following manner.
Sheela recorded her routine in the following manner.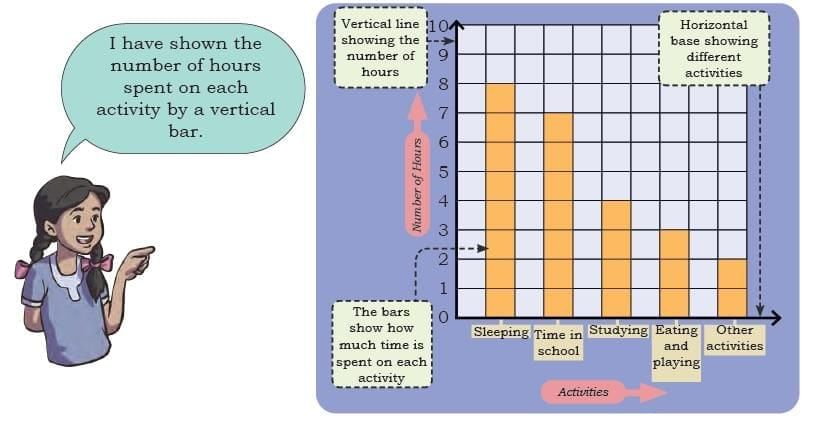 Observe Raman’s and Sheela’s routines and answer the following questions.
Observe Raman’s and Sheela’s routines and answer the following questions.
Q1: Whose daily routine shows more time spent on sleeping?
Ans: Raman spent 9 hours on sleeping and Sheela spent 8 hours on sleeping.
So, Raman’s daily routine shows more time spent on sleeping.
Q2: Who spends more hours in the school?
Ans: Raman spends 6 hours at school and Sheela spends 7 hours at school.
So, Sheela spends more hours in school.
Q3: How many more hours does Sheela spend studying compared to Raman?
Ans: Sheela spends 4 hours and Raman spends 2 hours in studying.
Difference = 4 – 2 = 2 hours
Sheela spends 2 more hours studying compared to Raman.
Q4: Is there any activity on which they spend the same amount of time? If yes, name the activity.
Ans: No, there is no activity on which they spend the same amount of time.
Q5: Based on their data, whose routine do you think is more balanced? Why?
Ans: Sheela’s routine appears to be more balanced with a good allocation for sleep, studying, and other activities.
Day in My Life
Q: Record your daily routine (24 hours) in hours and minutes, as necessary. Note the time spent on activities like sleeping, studying, playing, eating, and others.
Make a bar graph of the time you spend on different activities in the space given below.
Ans:
Whose Index Finger is Longer?
Cut long paper strips from waste paper. Give one strip (each of the same width) to each of your friends. Now, put the paper strip on your index finger and tear off the extra strip extending above your fingers.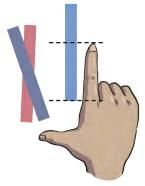 Paste these paper strips along the horizontal line in the given bar graph.
Paste these paper strips along the horizontal line in the given bar graph.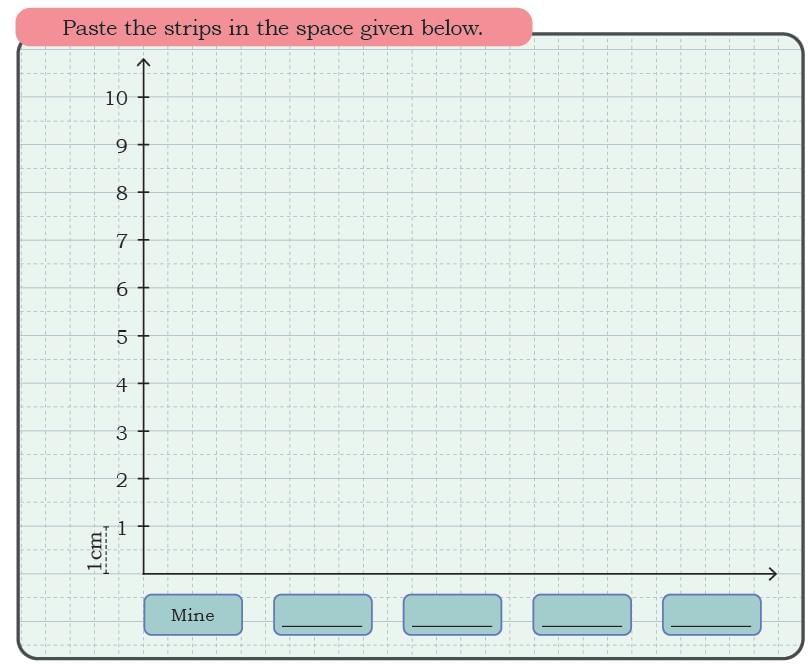
Write the answers to the following questions based on your graph.
1. Whose index finger is the longest?
2. The length of the longest index finger is _________ cm.
3. The smallest index finger is _________
4. It belongs to _________.
Ans: Do it yourself.
Food Wastage in the School Canteen
Rani stays in a residential school. Her school’s dining hall displays the amount of food wasted and the number of children the food could have fed. Given below is the data collected over the weekdays for different food items.
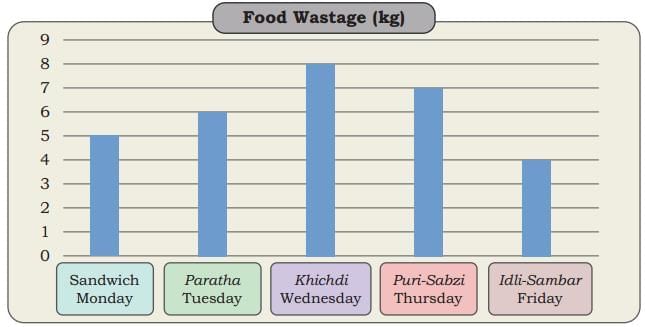
Q: Rani was shocked to see the data. What do you think about food wastage? How can we reduce the wastage of food? What can we do with the leftover food?
Ans: The food wastage is not only a waste of resources and money, but also disrespectful to the efforts of farmers and cooks.
The wastage of food can be reduced by:
(i) Preparing food according to the number of people eating.
(ii) Serving food in smaller portions.
(iii) Storing leftover food properly in the refrigerator.
(iv) Teaching children and adults the value of food.
The leftover food can be:
(i) Shared with neighbours, relatives, and friends.
(ii) Donated to NGOs for distribution to the needy.
(iii) Used creatively to make new dishes.
Observe the above graph and answer the following questions.
Q1: Which food item had the highest amount of wastage? _____________
Ans: Khichdi had the highest amount of wastage i.e., of 8 kg.
Q2: Which food item had the least amount of wastage? _______________
Ans: Idli-Sambhar had the least amount of wastage i.e., of 4 kg.
Q3: How much total food wastage was recorded in these days? _________
Ans: Total food wastage recorded in Monday to Friday = 5 + 6 + 8 + 7 + 4 = 30 kg
Q4: If 1 kg of food waste can feed 3 children, how many children could have been fed with the total food wasted?
Ans: 1 kg of food waste can feed 3 children.
30 kg of food waste can feed 3 × 30
= 90 children.
Q5: ________ day had less food wastage than day.
Ans: Friday had less food wastage than Wednesday.
Q6: If the same food items are to be repeated next week, can you predict which food item is likely to be wasted the most?
Ans: Khichdi had the highest wastage of 8 kg this week. So, Khichdi is most likely to be wasted the most again next week.
Page No. 187
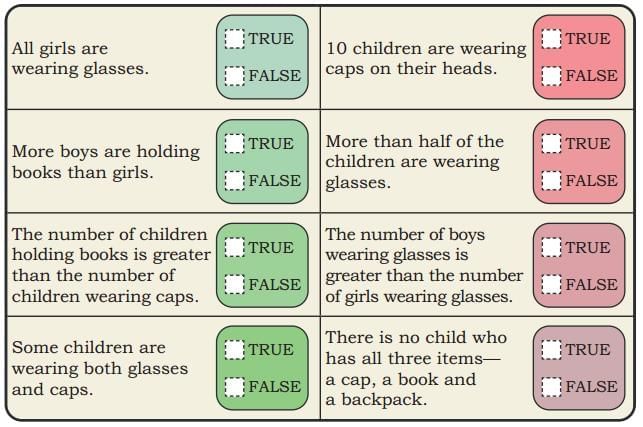
True or False
 Q: Observe the above picture carefully. Based on your observation, find out which of the following statements are true or false.
Q: Observe the above picture carefully. Based on your observation, find out which of the following statements are true or false.
 Ans:
Ans: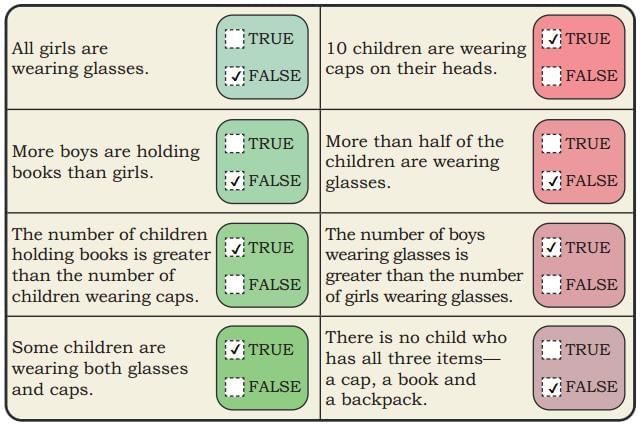


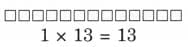

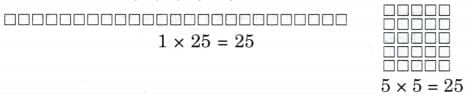


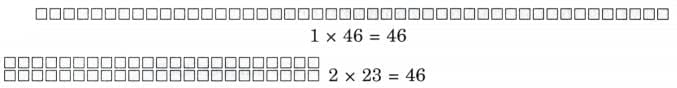
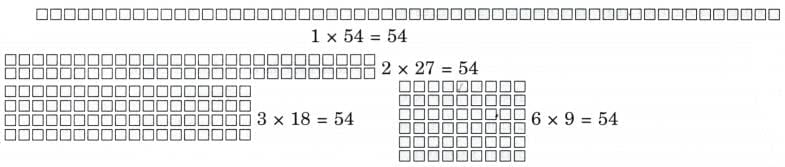
 Ans:
Ans: 4 divides 16, 36 and 48 exactly.
4 divides 16, 36 and 48 exactly. Ans:
Ans:





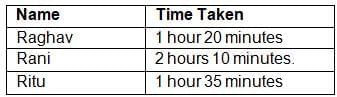
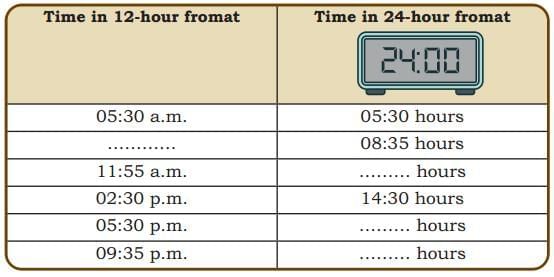 Ans:
Ans: 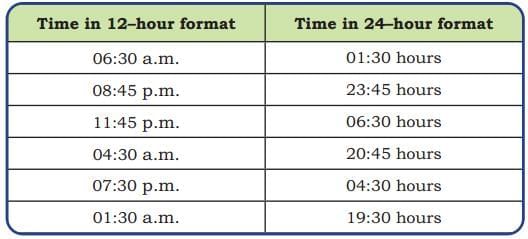 Ans:
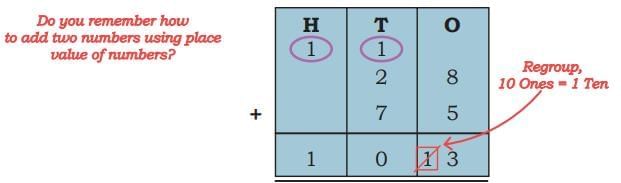
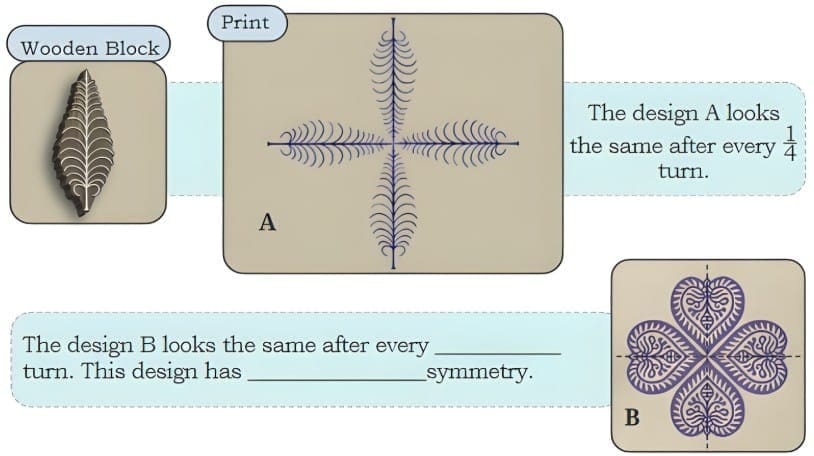
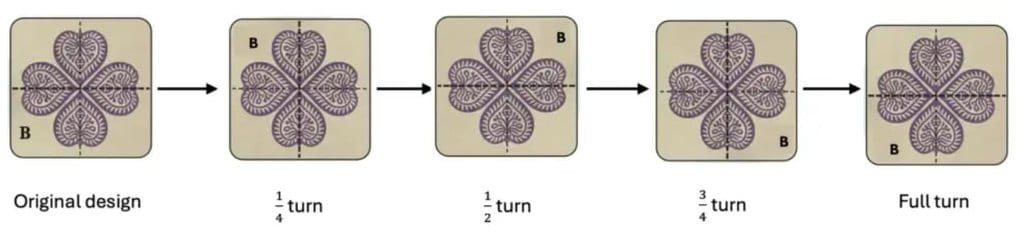
Ans:  Q: Do you notice the use of a new unit, ‘seconds’ in the picture?
Q: Do you notice the use of a new unit, ‘seconds’ in the picture?
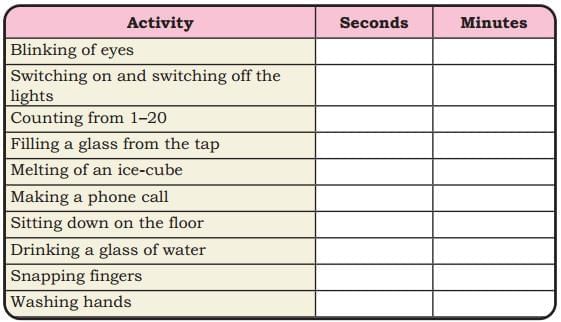 Ans:
Ans: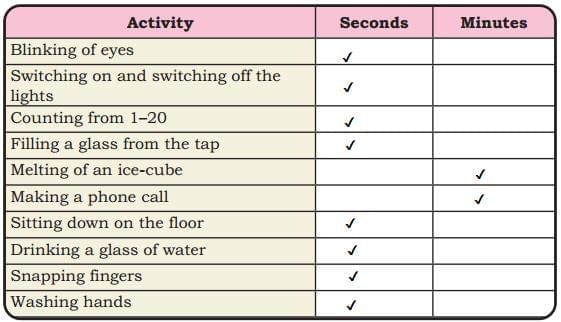
 Ans:
Ans:
 Ans:
Ans: Ans:
Ans: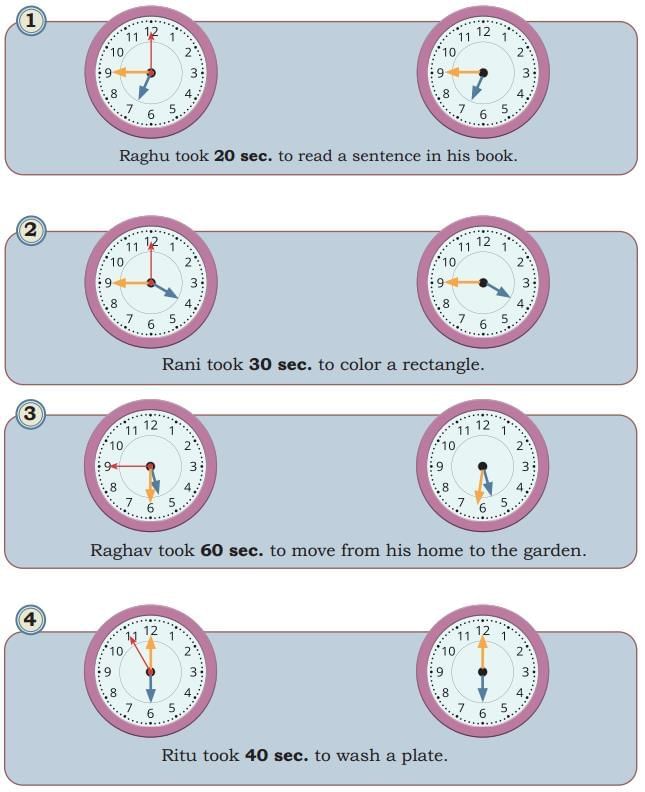 Ans:
Ans:  Ans:
Ans: 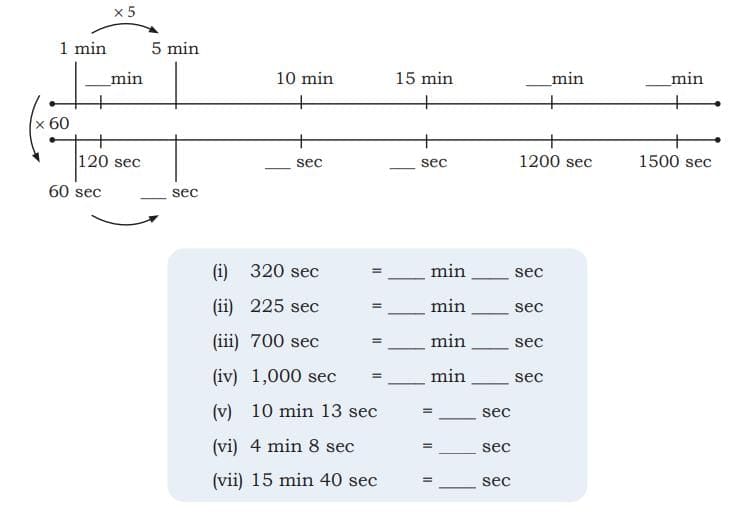



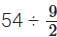
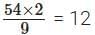



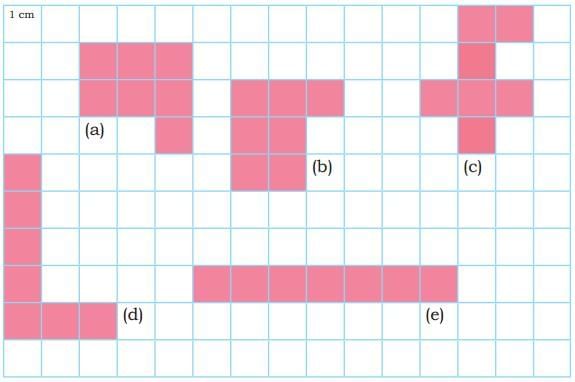

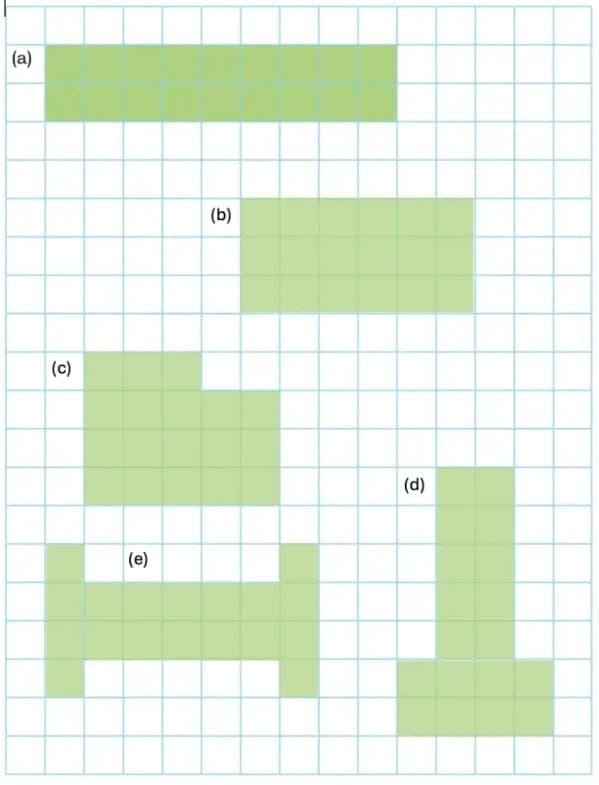
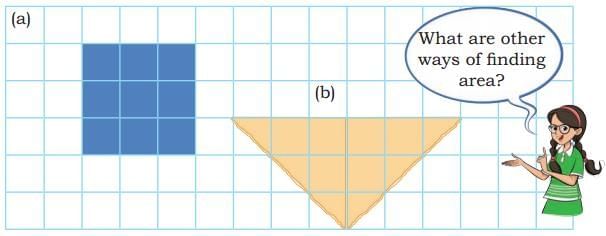
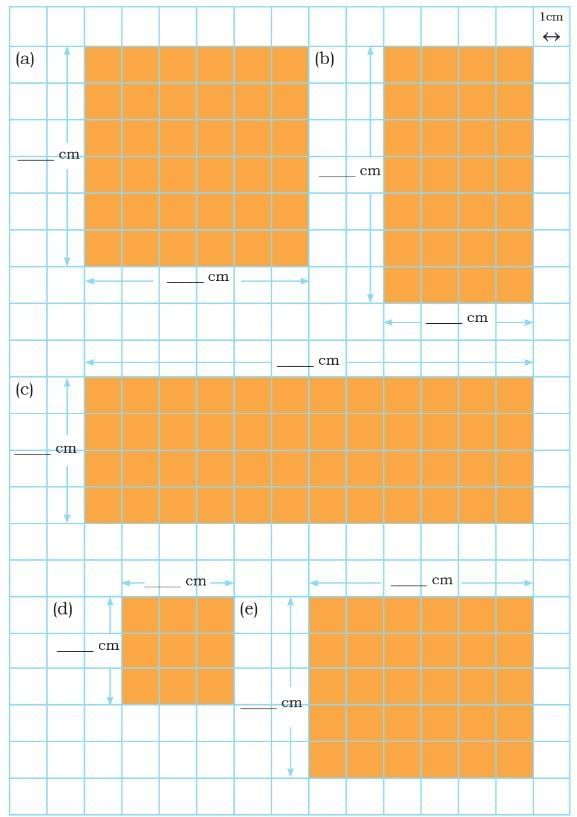

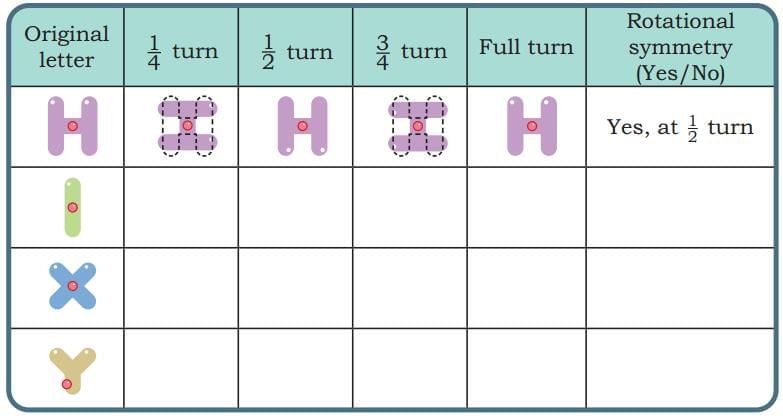
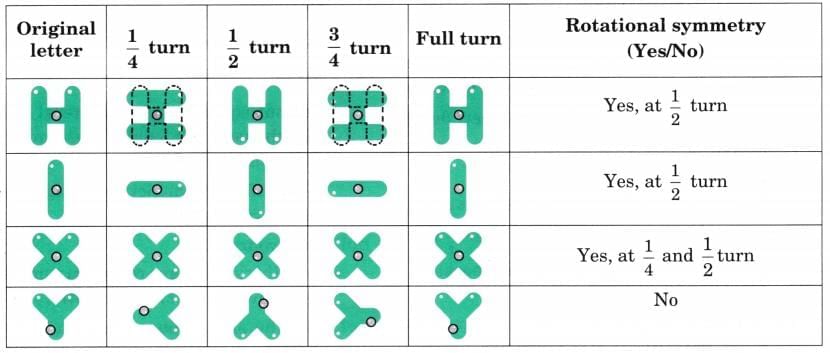










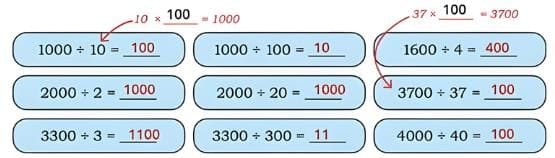
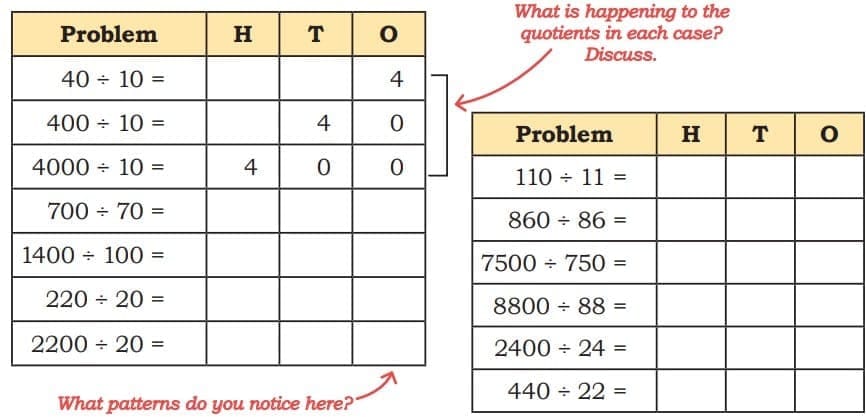
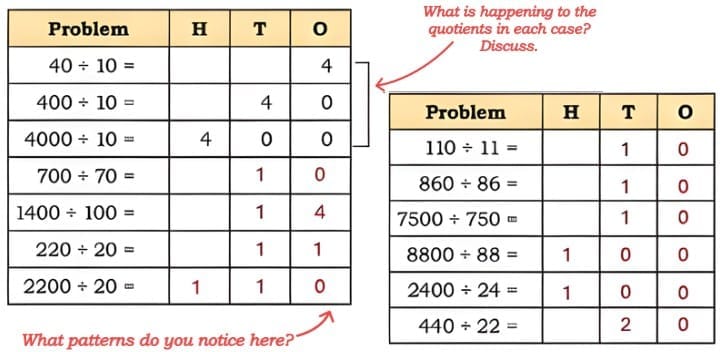
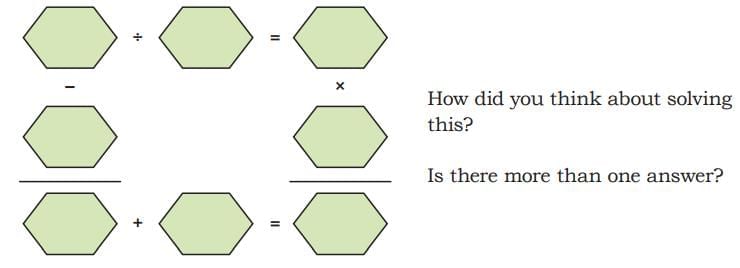
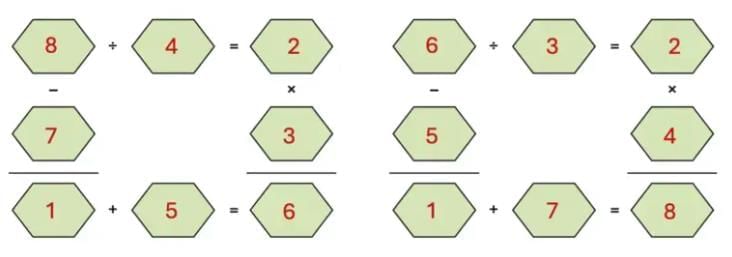
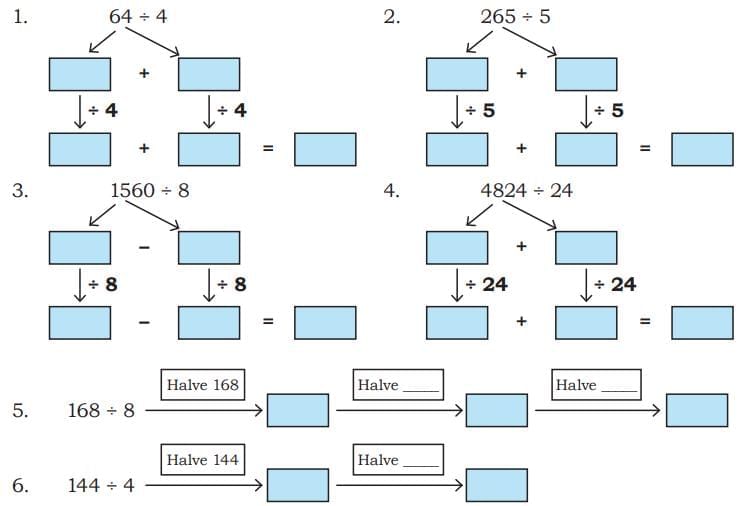
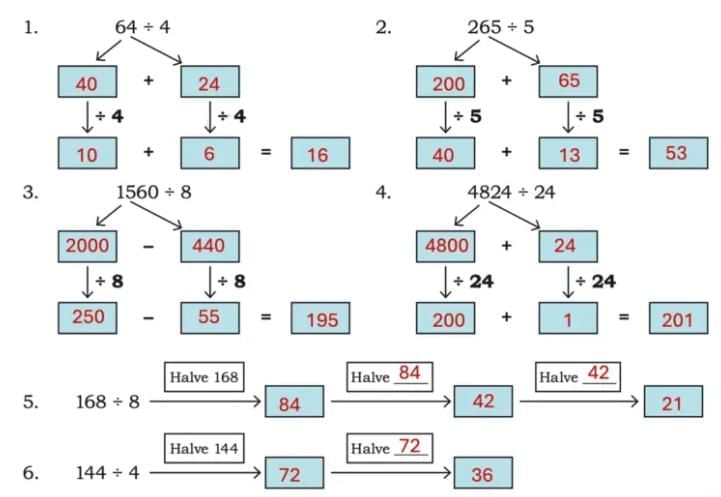
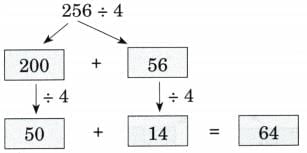
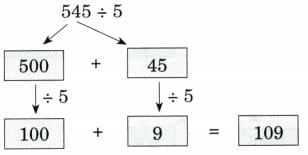
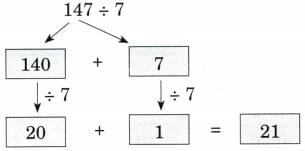
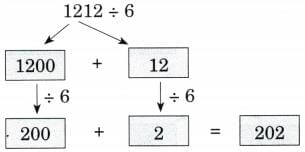
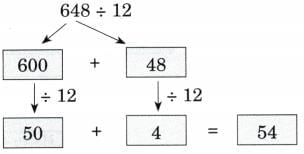
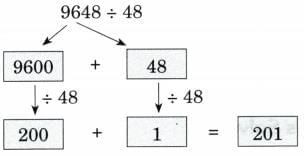
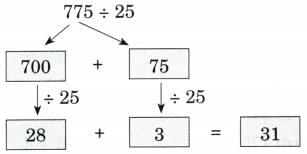
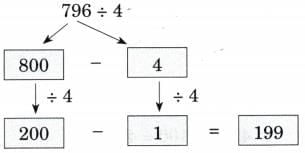

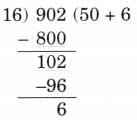
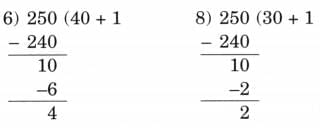
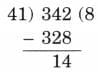
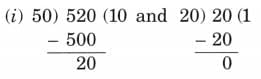
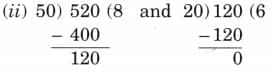

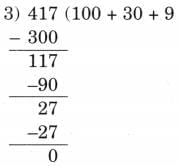

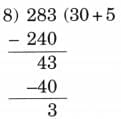


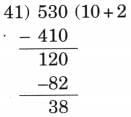
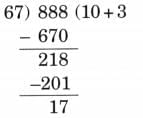

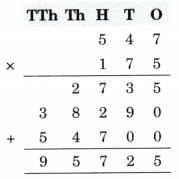

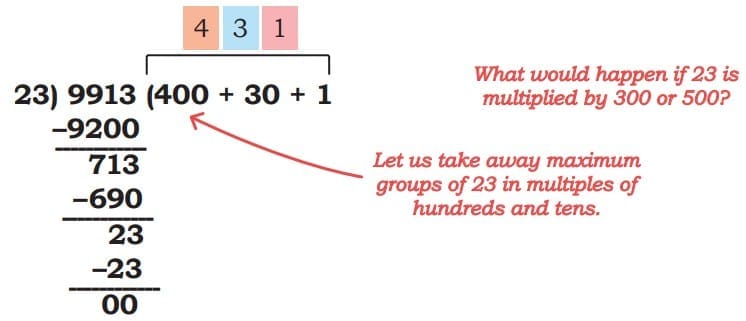
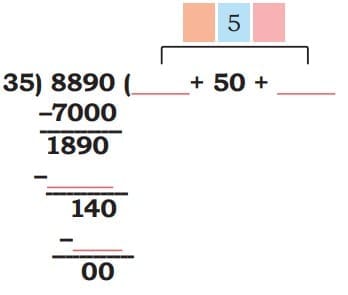

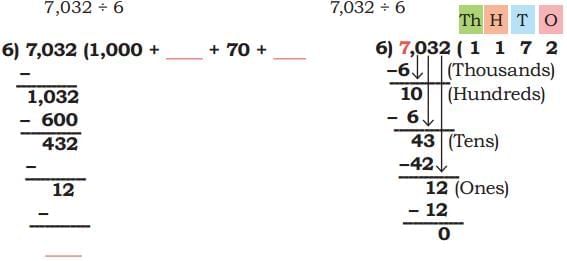


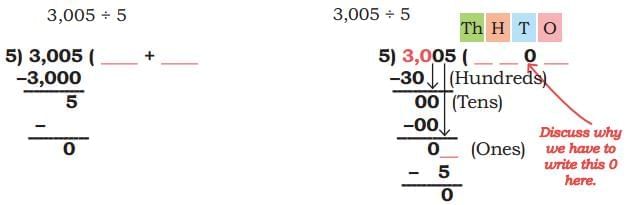
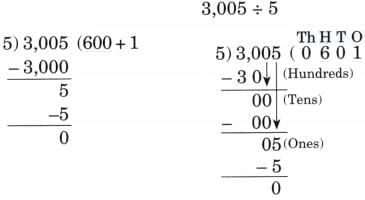
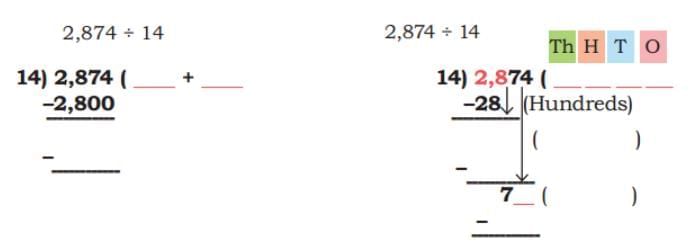

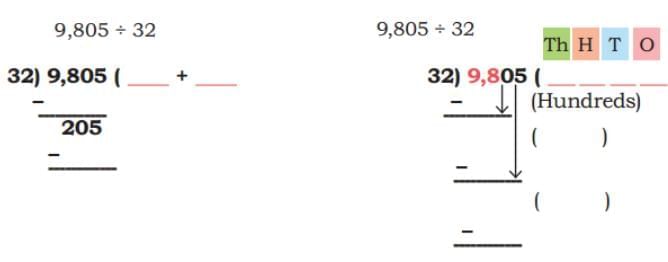

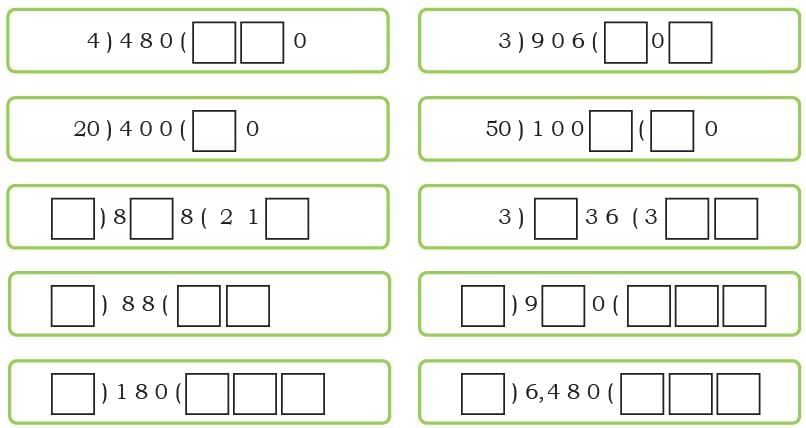
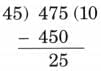




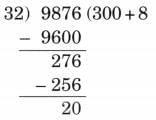




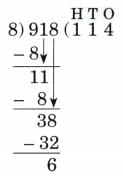
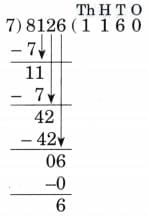
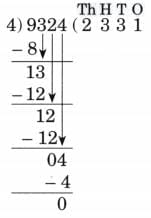
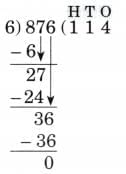
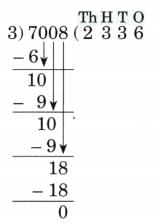
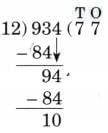

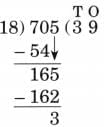

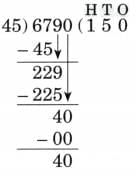
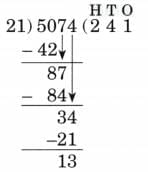
 Ans:
Ans: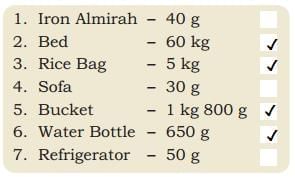
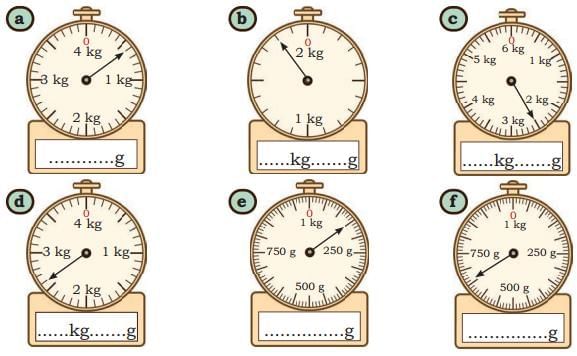 Ans:
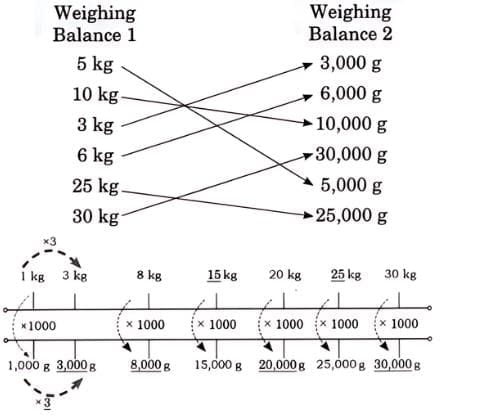
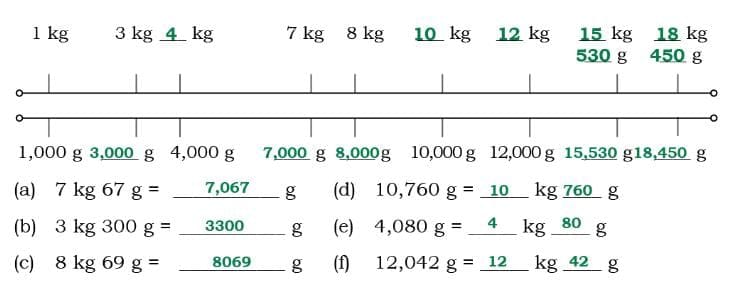
Ans: From parts (a) to (d), each small division on the scale represents 100 g, and in parts (e) and (f), each small division on the scale represents 10 g.
From parts (a) to (d), each small division on the scale represents 100 g, and in parts (e) and (f), each small division on the scale represents 10 g.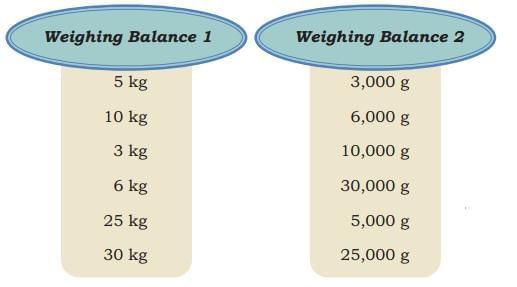
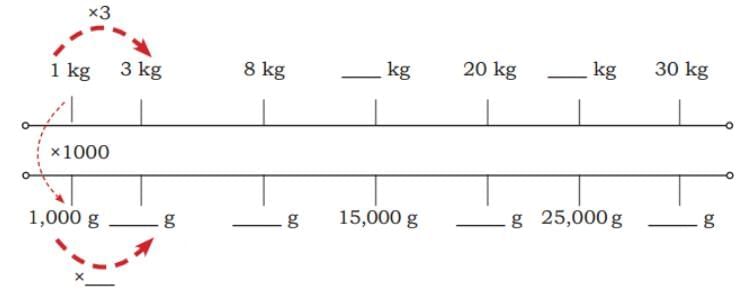
 Ans:
Ans:
 Ans:
Ans:
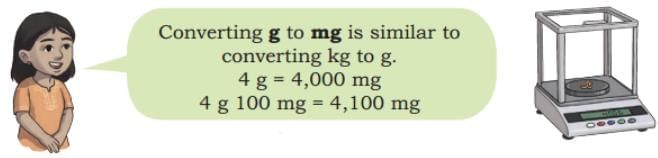
 Ans:
Ans: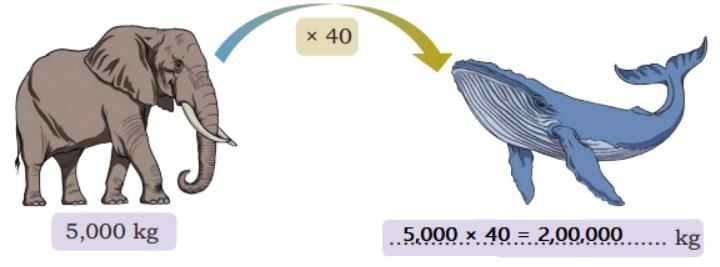
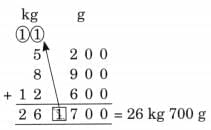
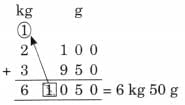


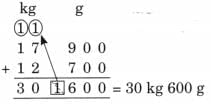
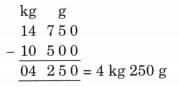
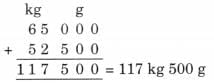
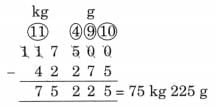
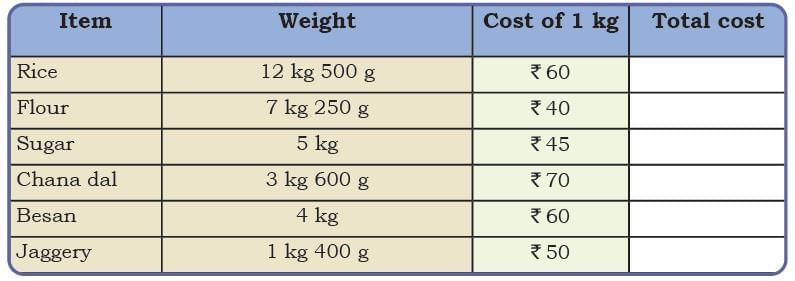 Ans:
Ans:
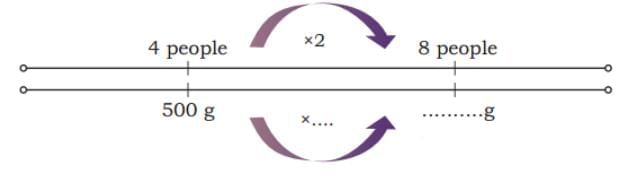 Ans:
Ans: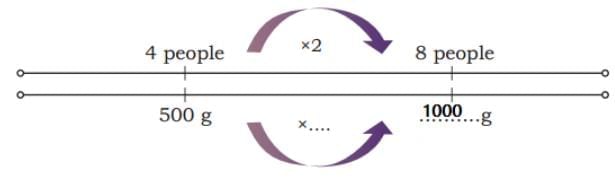
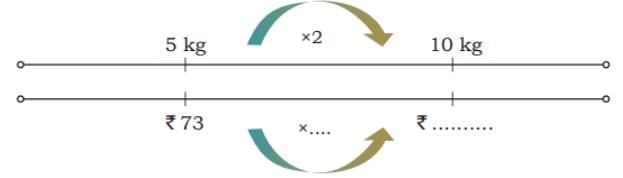 Ans:
Ans: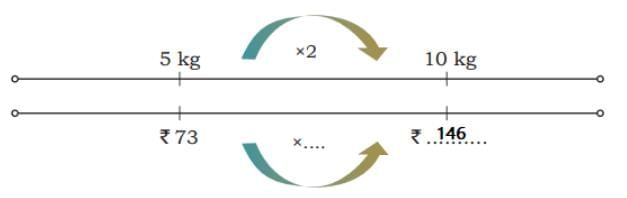
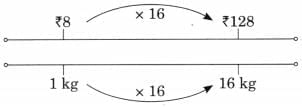
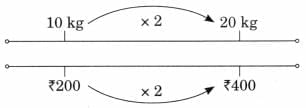
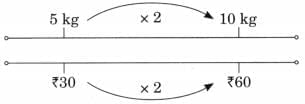
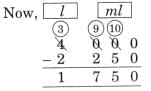
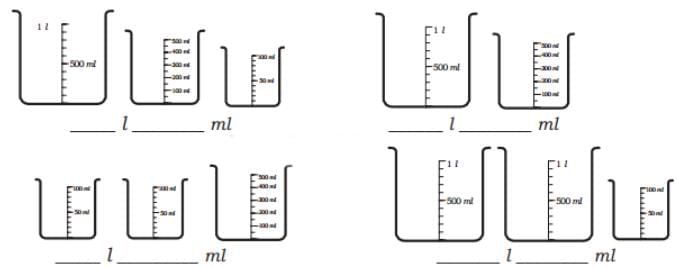 Ans: First Jug: 1 litre + 500 mL + 100 mL = 1 litre 600 mL
Ans: First Jug: 1 litre + 500 mL + 100 mL = 1 litre 600 mL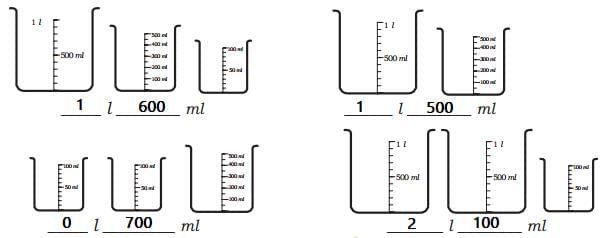

 Ans:
Ans:
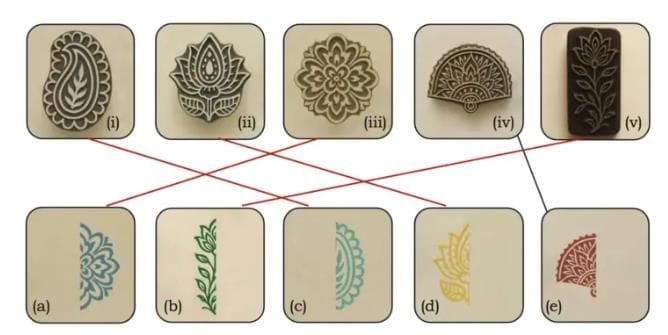
 Who do you think is correct and why?
Who do you think is correct and why?
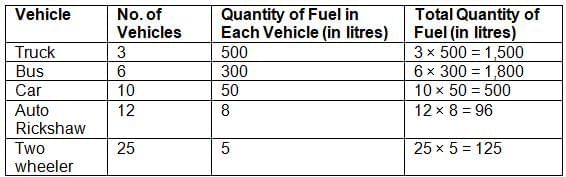
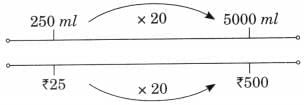
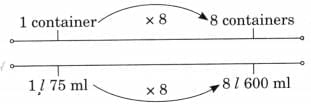
 Ans:
Ans: Ans:
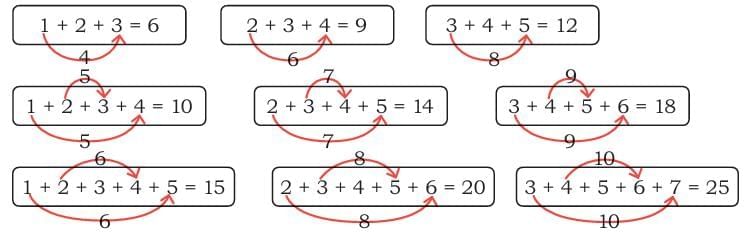
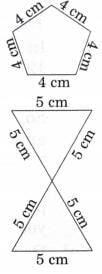
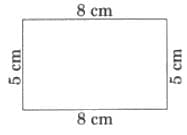
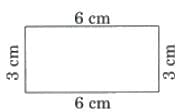
Ans: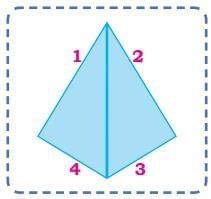 Here are three possible shapes.
Here are three possible shapes.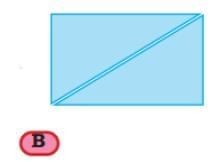
 Ans:
Ans: Ans:
Ans: 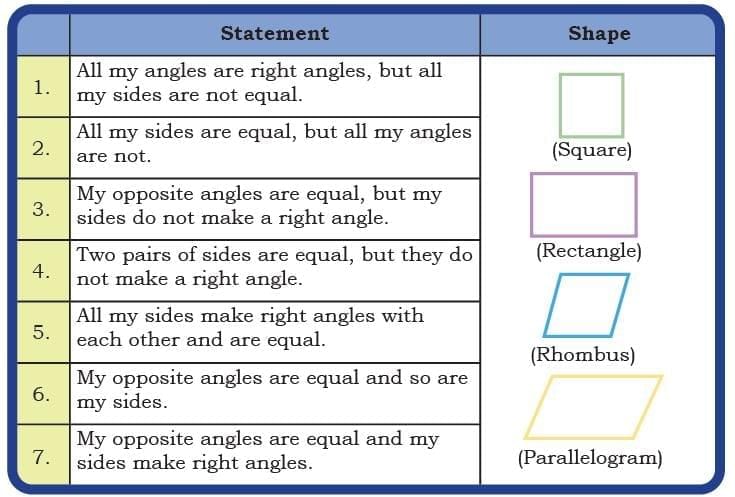 Ans:
Ans: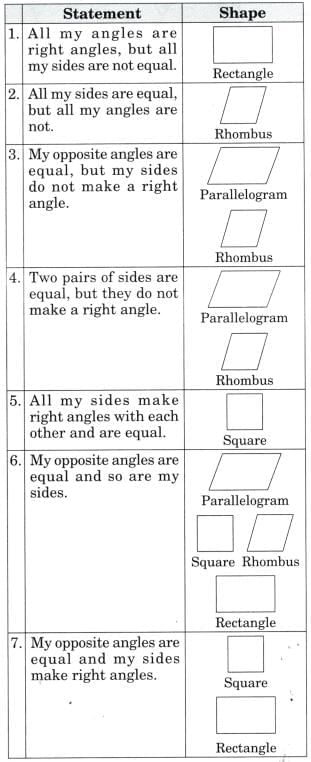
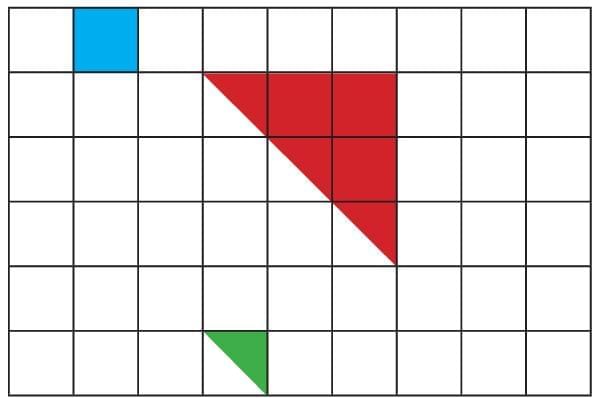
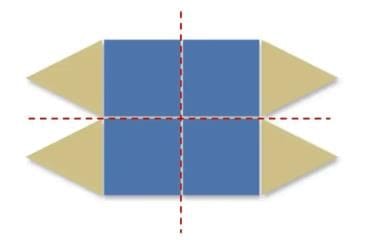
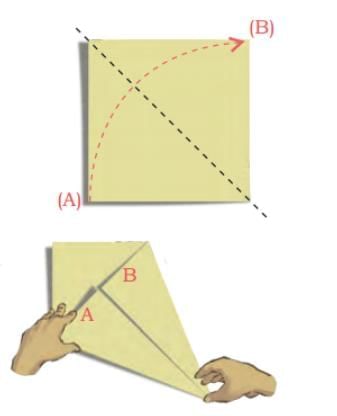 Q: What shapes do you see in the kite?
Q: What shapes do you see in the kite? Ans:
Ans: