Q1: A quadrilateral has three acute angles, each measure 80°. What is the measure of the fourth angle?
Solution:
Let x be the measure of the fourth angle of a quadrilateral.
Sum of the four angles of a quadrilateral = 360°
80° + 80° + 80° + x = 360°
x = 360° – (80° + 80° + 80°)
x = 360° – 240°
x = 120°
Hence, the fourth angle is 120°.
Q2: In a quadrilateral ABCD, the measure of the three angles A, B and C of the quadrilateral is 110°, 70° and 80°, respectively. Find the measure of the fourth angle.
Solution: Let,
∠A = 110°
∠B = 70°
∠C = 80°
∠D = x
We know that the sum of all internal angles of quadrilateral ABCD is 360°.
∠A + ∠B+ ∠C+∠D = 360°
110° + 70° + 80° + x = 360°
260° + x = 360°
x = 360° – 260°
x = 100°
Therefore, the fourth angle is 100°.
Q3: The opposite angles of a parallelogram are (3x + 5)° and (61 – x)°. Find the measure of four angles.
Solution:
Given,
(3x + 5)° and (61 – x)° are the opposite angles of a parallelogram.
We know that the opposite angles of a parallelogram are equal.
Therefore,
(3x + 5)° = (61 – x)°
3x + x = 61° – 5°
4x = 56°
x = 56°/4
x = 14°
⇒ 3x + 5 = 3(14) + 5 = 42 + 5 = 47
61 – x = 61 – 14 = 47
The measure of angles adjacent to the given angles = 180° – 47° = 133°
Hence, the measure of four angles of the parallelogram are 47°, 133°, 47°, and 133°.
Q4: A diagonal and a side of a rhombus are of equal length. Find the measure of the angles of the rhombus.
Solution:
Let ABCD be the rhombus.
Thus, AB = BC = CD = DA
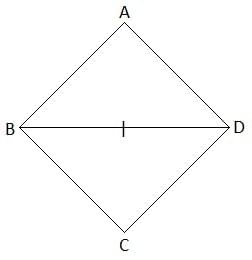
Given that a side and diagonal are equal.
AB = BD (say)
Therefore, AB = BC = CD = DA = BD
Now, all the sides of a triangle ABD are equal.
Therefore, ΔABD is an equilateral triangle.
Similarly,
ΔBCD is also an equilateral triangle.
Thus, ∠A = ∠ABD = ∠ADB = ∠DBC = ∠C = ∠CDB = 60°
∠B = ∠ABD + ∠DBC = 60° + 60° = 120°
And
∠D = ∠ADB + ∠CDB = 60° + 60° = 120°
Hence, the angles of the rhombus are 60°, 120°, 60° and 120°.
Q5: In a trapezium PQRS, PQ || RS, ∠P : ∠S = 3 : 2 and ∠Q : ∠R = 4 : 5. Find the angles of the trapezium.
Solution:
Given,
∠P : ∠S = 3 : 2
∠Q : ∠R = 4 : 5
Let 3x and 2x be the measures of angles P and S.
And let 4x and 5x be the measures of angle Q and R.
As we know, the sum of adjacent angles at the corners of non-parallel sides of a trapezium = 360°
∠P + ∠S = 180°
3x + 2x = 360°
5x = 180°
x = 180°/5 = 36°
So, 3x = 3(36°) = 108°
2x = 2(36°) = 72°
Similarly,
4x + 5x = 180°
9x = 180°
x = 180°/9 = 20°
So, 4x = 4(20°) = 80°
5x = 5(20°) = 100°
Therefore, the angles of the trapezium are ∠P = 108°, ∠Q = 80, ∠R = 100 and ∠S = 72.
Q6: The diagonals of a rhombus are 12 cm and 7.5 cm. Find the area of a rhombus.
Solution:
Given: Length of diagonal 1 = 12 cm
Length of diagonal 2 = 7.5 cm
We know that,
Area of a rhombus = (1/2) × Diagonal 1× Diagonal 2 square units
A = (½)×12×7.5
A = 6×7.5
A = 45 cm2
Hence, the area of a rhombus is 45 cm2.
Q7: ABCD is a quadrilateral, whose angles are ∠A = 5(a+2)°, ∠B = 2(2a+7)°, ∠C = 64°, ∠D = ∠C-8°. Determine the value of ∠A.
Solution:
Given that, ∠A = 5(a+2)°, ∠B = 2(2a+7)°, ∠C = 64°, ∠D = ∠C-8°
Hence, ∠D = 64° – 8°
∠D = 56°
As we know,
∠A+∠B+∠C+∠D = 360°
Now, substitute the values, we get
5(a+2)° + 2(2a+7)° + 64°+56° = 360°
5a°+10°+4a°+14° +64° +56° = 360°
9a° + 144° = 360°
9a° = 360° – 144°
9a° = 216°
a° = 216°/9
a° = 24°
Hence, the value of ∠A is:
∠A = 5(a+2)° = 5(24°+2°) = 5 (26°) = 130°
Therefore, ∠A = 130°.
Q8: The three angles of a quadrilateral are 60°, 90°, 110°. Determine the fourth angle.
Solution:
We know that the sum of interior angles of a quadrilateral is 360°.
Given three angles are 60°, 90° and 110°.
Let the unknown angle be “x”.
By using the property of quadrilateral,
60° + 90° + 110° + x = 360°
260° + x = 360°
x = 360° – 260°
x = 100°.
Hence, the fourth angle of a quadrilateral is 100°.
Q9: If the diagonals of a rhombus are 12 cm and 7.5 cm, what is the area of the rhombus?
Solution:
Given: Length of diagonal 1 = 12 cm
Length of diagonal 2 = 7.5 cm
We know that,
Area of a rhombus = (1/2) × Diagonal 1× Diagonal 2 square units
A = (½)×12×7.5
A = 6×7.5
A = 45 cm 2
Hence, the area of a rhombus is 45 cm 2 .
Q10: If two angles of a quadrilateral are 76° and 68°, and the other two angles are in the ratio of 5: 7, what are the measures of these two angles?
Solution:
Given that two angles are 76° and 68°.
Let’s denote the other two angles as 5x and 7x.
As we know, the sum of interior angles of a quadrilateral is 360°.
Therefore, 76°+68°+5x + 7x = 360°
144° + 12x = 360°
12x = 360° – 144°
12x = 216°
x = 216°/12
x = 18°
Hence, the other two angles are:
5x = 5(18)° = 90°
7x = 7(18°) = 126°.
 Example: 5 cows → 5 sticks.
Example: 5 cows → 5 sticks.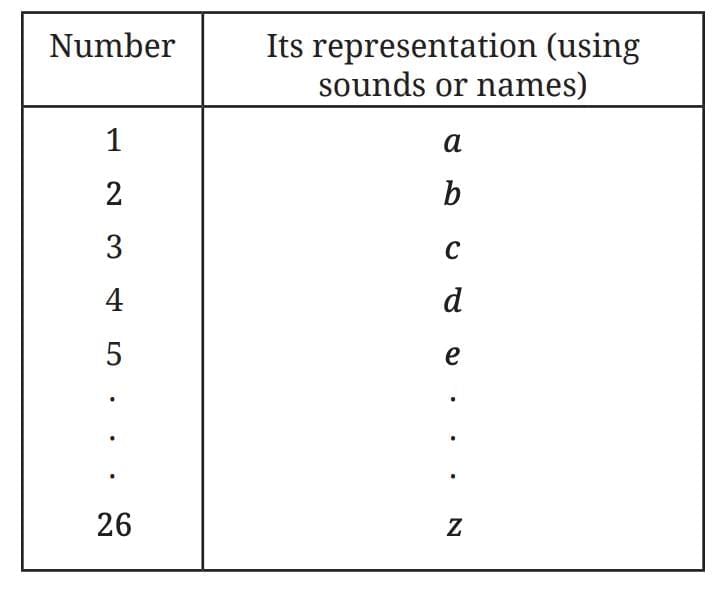 Example: “a, b, c…”
Example: “a, b, c…” This is an early form of written numbers.
This is an early form of written numbers.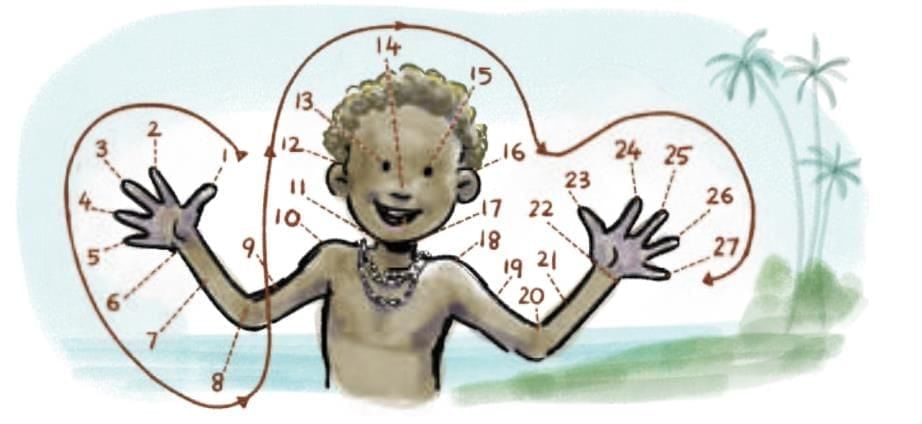 Hands, fingers, body parts used to count (e.g., Papua New Guinea).
Hands, fingers, body parts used to count (e.g., Papua New Guinea). Marks on bones/walls (e.g., Ishango bone, 20,000–35,000 years ago; Lebombo bone, 44,000 years ago).
Marks on bones/walls (e.g., Ishango bone, 20,000–35,000 years ago; Lebombo bone, 44,000 years ago). 1 = urapon, 2 = ukasar, 3 = ukasar-urapon, 4 = ukasar-ukasar, …
1 = urapon, 2 = ukasar, 3 = ukasar-urapon, 4 = ukasar-ukasar, …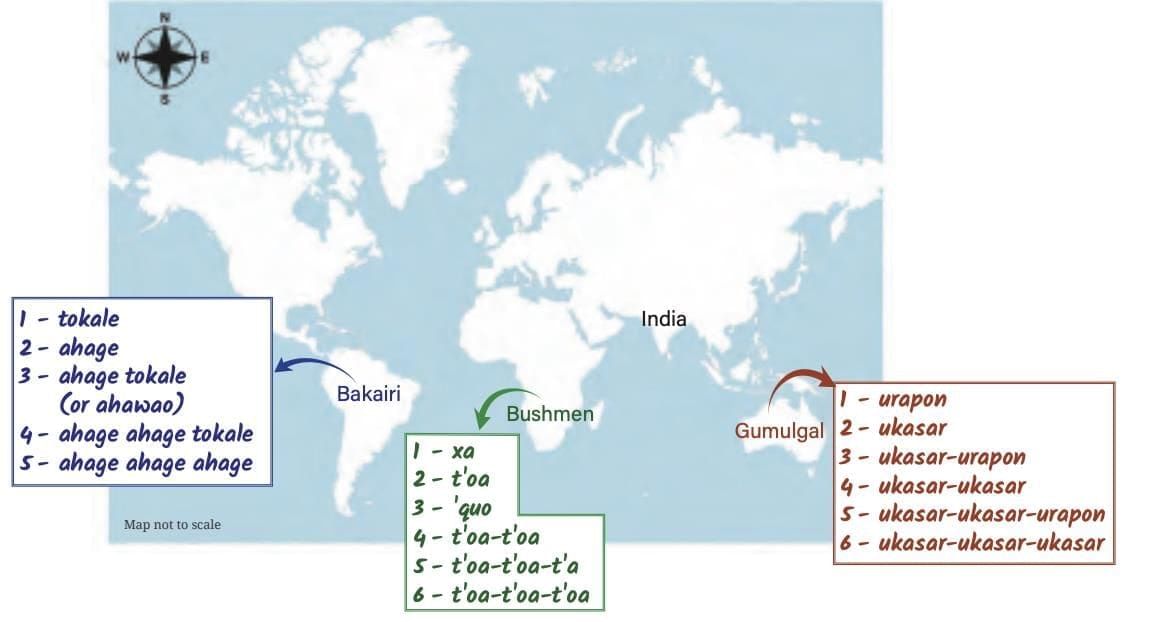 Similar systems in South America & South Africa.
Similar systems in South America & South Africa.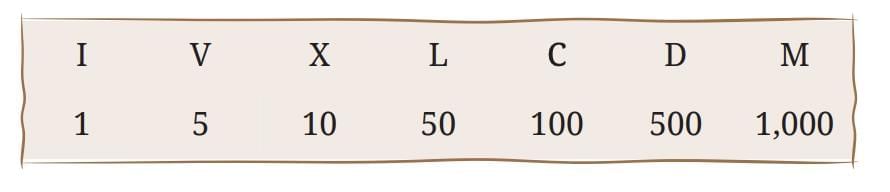 Symbols: I (1), V (5), X (10), L (50), C (100), D (500), M (1000).
Symbols: I (1), V (5), X (10), L (50), C (100), D (500), M (1000).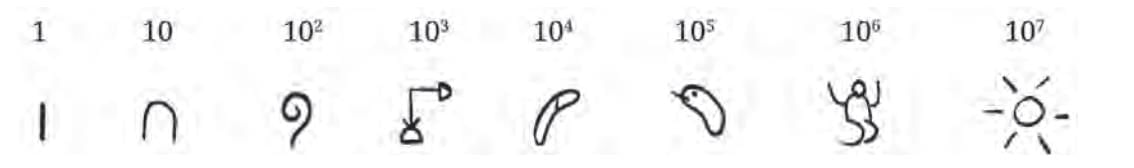 Landmark numbers: 1, 10, 100, … (powers of 10, base-10 system).
Landmark numbers: 1, 10, 100, … (powers of 10, base-10 system).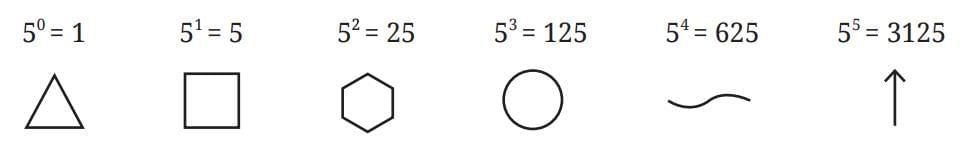 Example: Base-5 system → 1, 5, 25, 125, …
Example: Base-5 system → 1, 5, 25, 125, …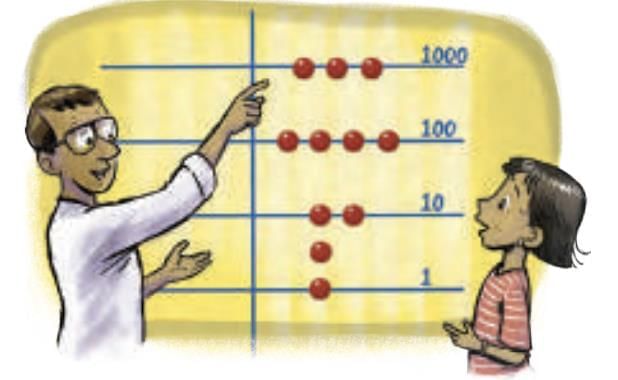 Counters on lines representing powers of 10.
Counters on lines representing powers of 10. Developed base-60 (sexagesimal) system.
Developed base-60 (sexagesimal) system.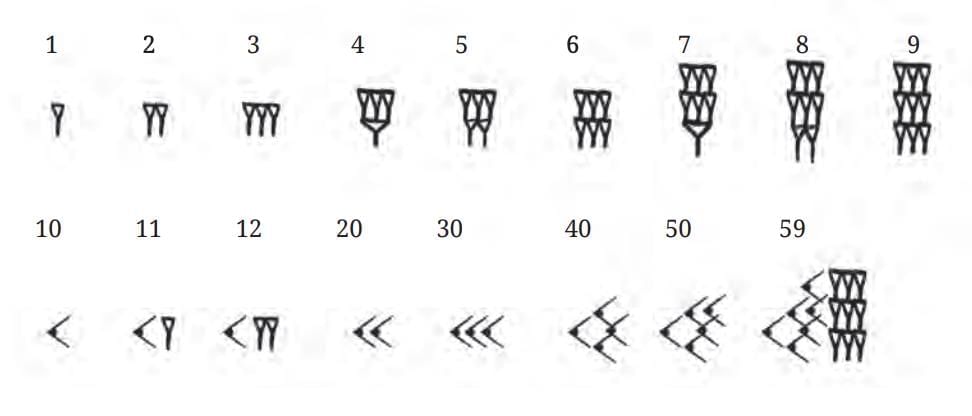 Symbols: 1 and 10.
Symbols: 1 and 10.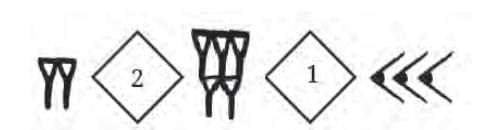 Numbers grouped by powers of 60 (e.g., 7530 = 2×3600 + 5×60 + 30).
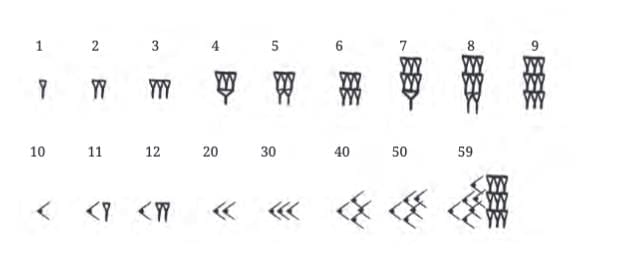
Numbers grouped by powers of 60 (e.g., 7530 = 2×3600 + 5×60 + 30). Dots = 1, Bars = 5; numbers written vertically.
Dots = 1, Bars = 5; numbers written vertically. Vertical position of the symbol indicates powers of 10.
Vertical position of the symbol indicates powers of 10. Uses place value to represent numbers.
Uses place value to represent numbers.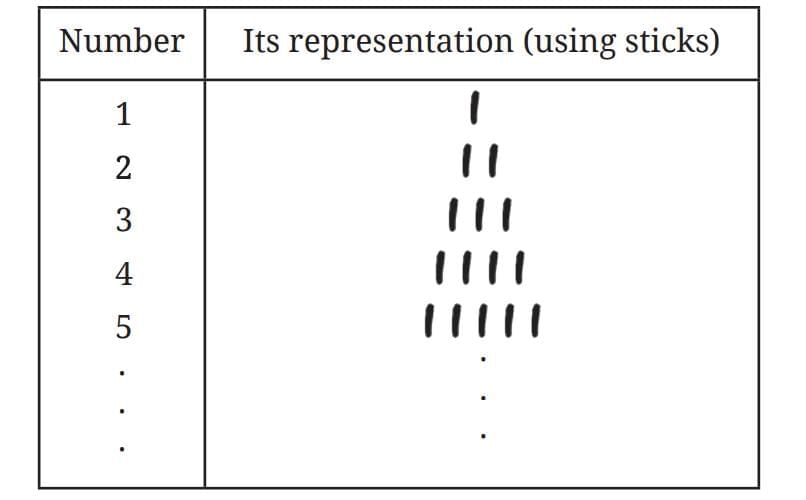 Sticks/Pebbles/Seeds (Method 1)
Sticks/Pebbles/Seeds (Method 1)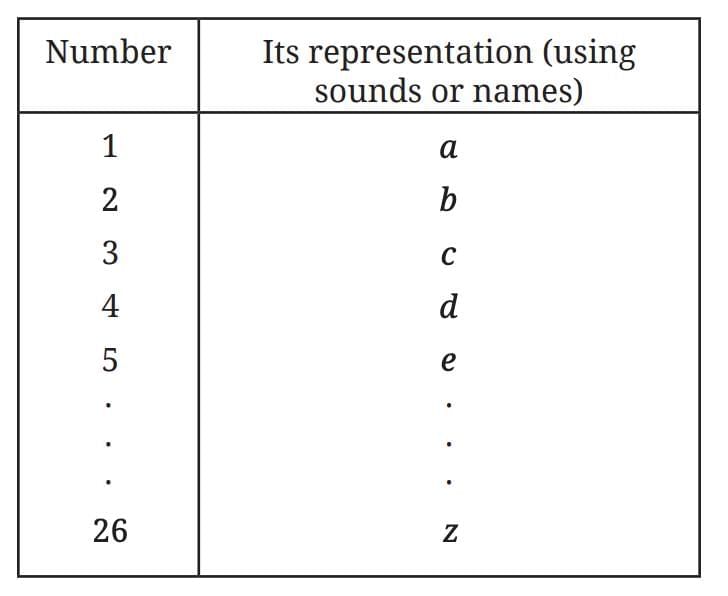 Sounds/Names (Method 2) → Limited by available sounds/letters.
Sounds/Names (Method 2) → Limited by available sounds/letters.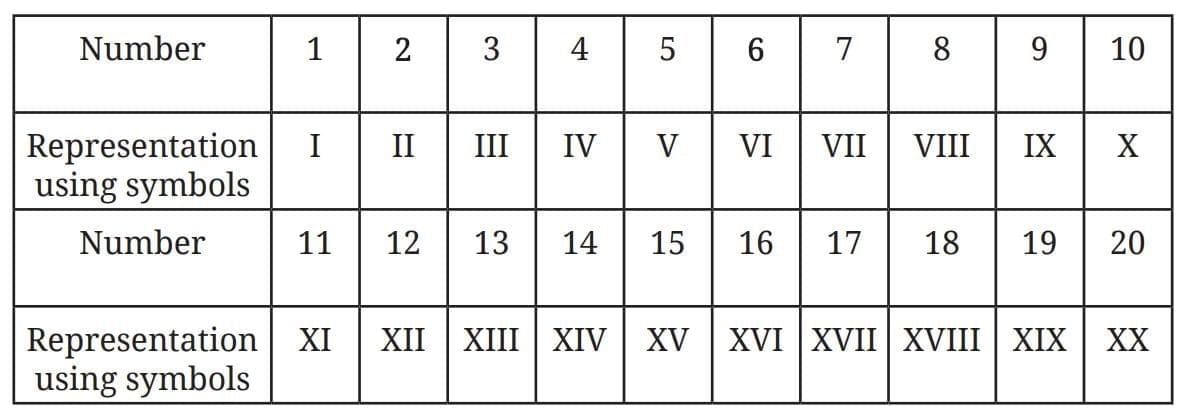 Written symbols (Method 3) → e.g., Roman numerals.
Written symbols (Method 3) → e.g., Roman numerals. Lebombo Bone (44k yrs old) – lunar calendar.
Lebombo Bone (44k yrs old) – lunar calendar. Gumulgal (Australia): Count in 2’s → Numbers = combinations of 2’s & 1’s.
Gumulgal (Australia): Count in 2’s → Numbers = combinations of 2’s & 1’s.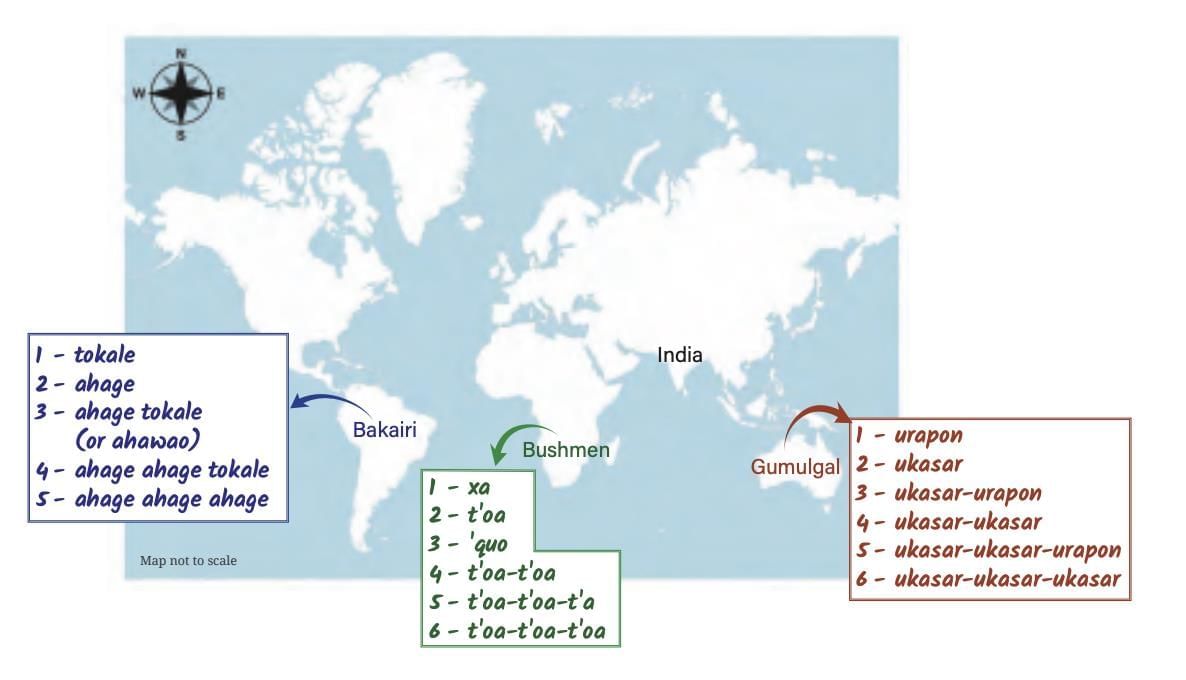 Common groups in history: 2, 5, 10, 20.
Common groups in history: 2, 5, 10, 20.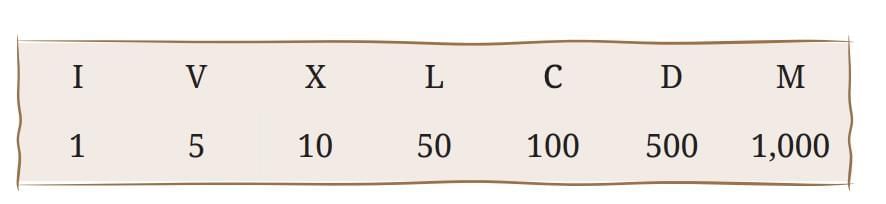
 Base-n system: Landmark numbers = powers of n
Base-n system: Landmark numbers = powers of n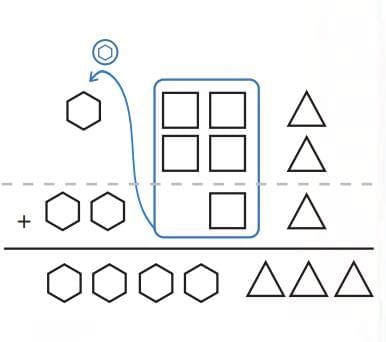 Advantages: Consistent grouping, easier addition & multiplication.
Advantages: Consistent grouping, easier addition & multiplication.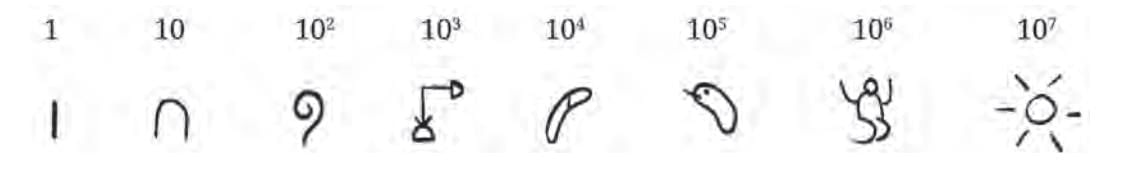 Base-10, symbols for 1, 10, 100, 1000, 10,000…
Base-10, symbols for 1, 10, 100, 1000, 10,000… Build numbers by repeating symbols. For example 324 which equals 100 + 100 + 100 + 10 + 10 + 4 is written as
Build numbers by repeating symbols. For example 324 which equals 100 + 100 + 100 + 10 + 10 + 4 is written as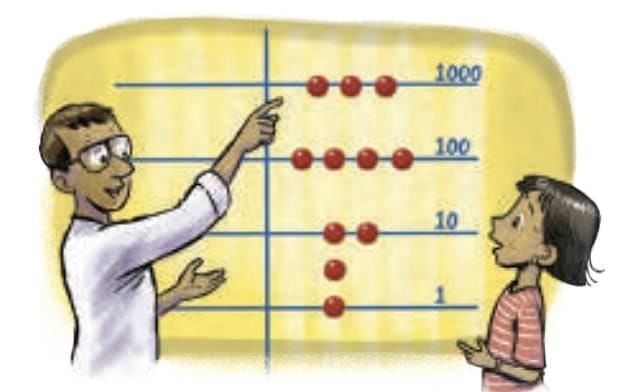 Decimal-based calculating tool.
Decimal-based calculating tool.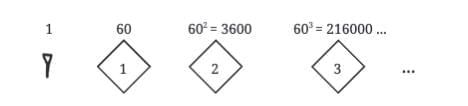
 Two main wedge-shaped symbols (cuneiform writing) for numbers.
Two main wedge-shaped symbols (cuneiform writing) for numbers.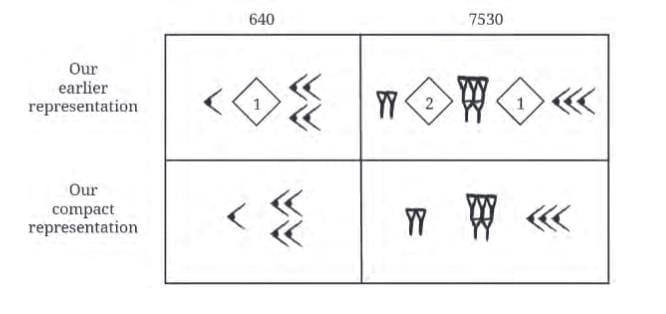 Numbers formed by repeating and combining these symbols.
Numbers formed by repeating and combining these symbols. Numbers are written vertically, lowest value at bottom.
Numbers are written vertically, lowest value at bottom.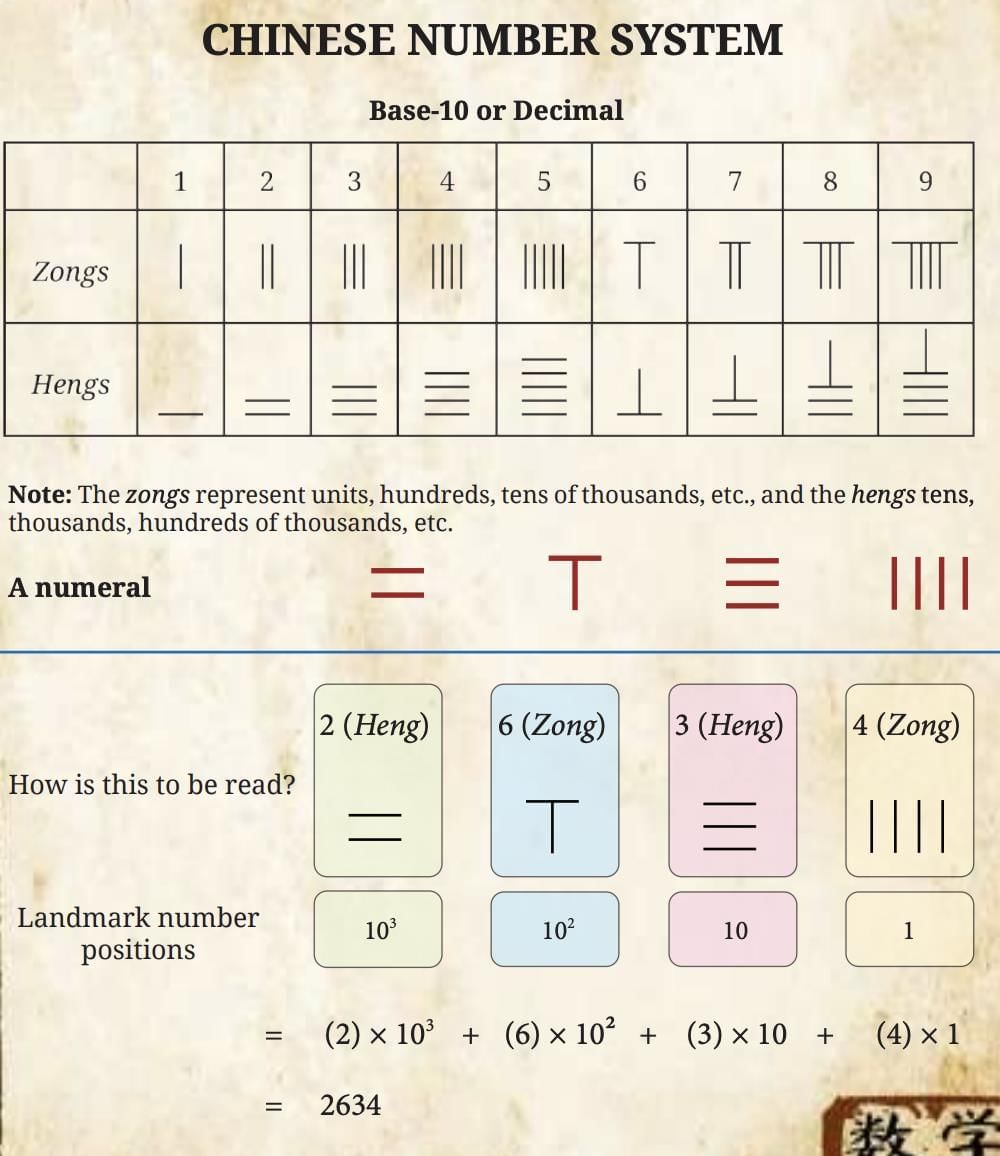

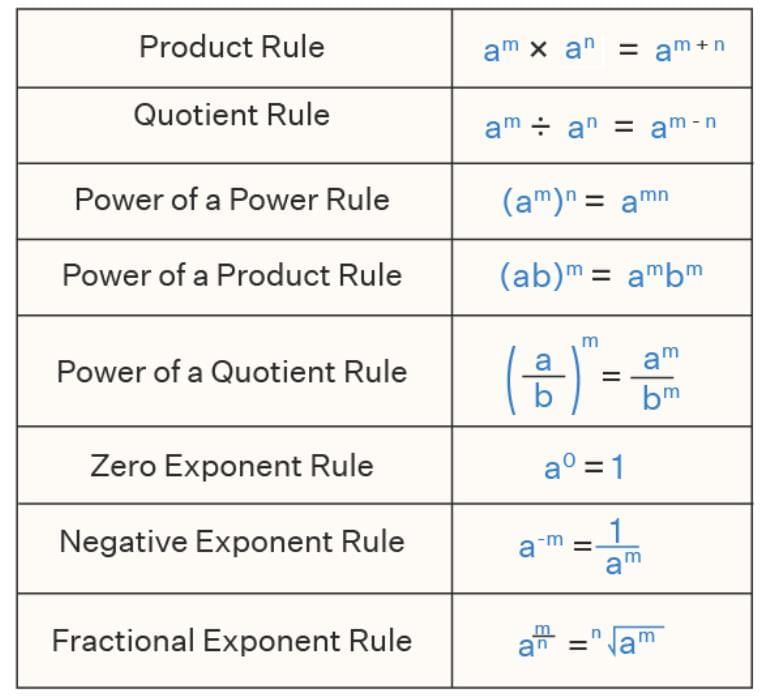
 Example: 8² ÷ 2² = (8 ÷ 2)² = 4²
Example: 8² ÷ 2² = (8 ÷ 2)² = 4²

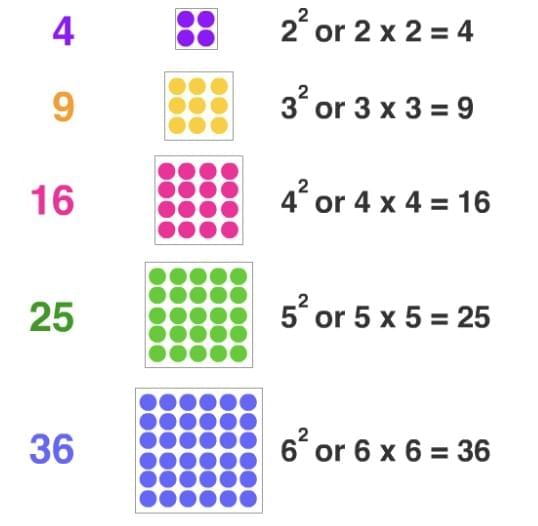 Squares of natural numbers = perfect squares.
Squares of natural numbers = perfect squares.
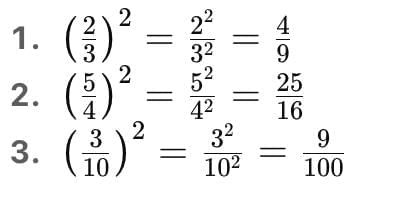
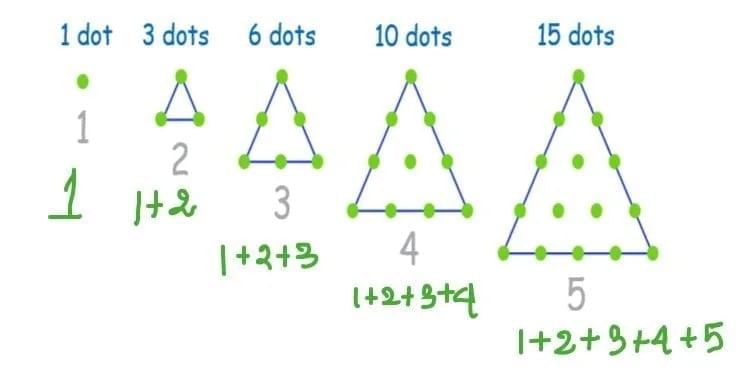 Sum of two consecutive triangular numbers = perfect square.
Sum of two consecutive triangular numbers = perfect square.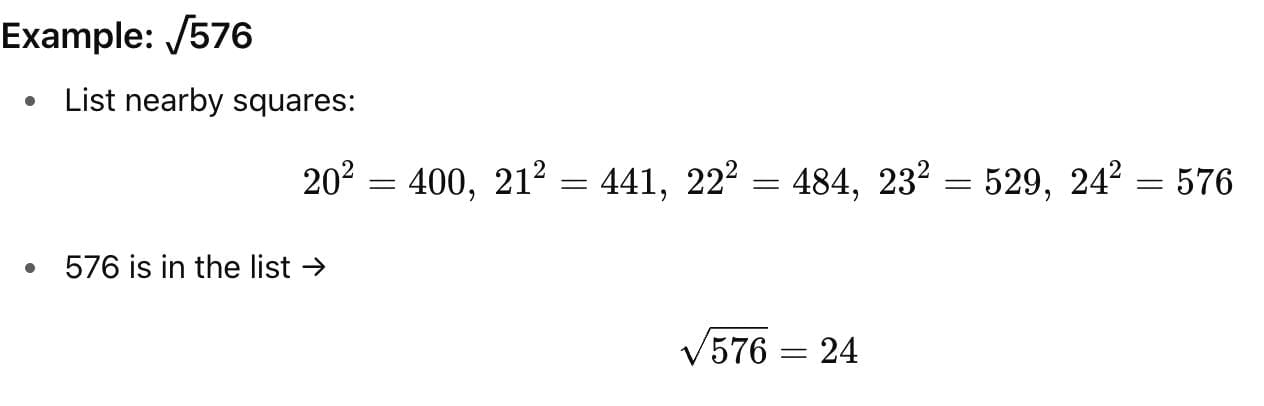 Listing Squares → compare with nearby perfect squares.
Listing Squares → compare with nearby perfect squares. Successive Subtraction of Odd Numbers → subtract until 0.
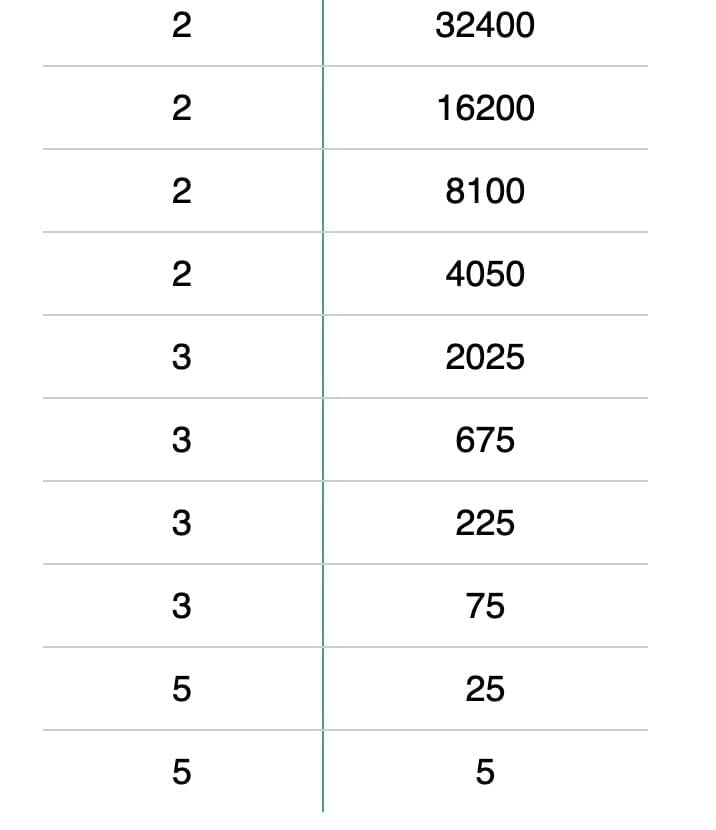
Successive Subtraction of Odd Numbers → subtract until 0.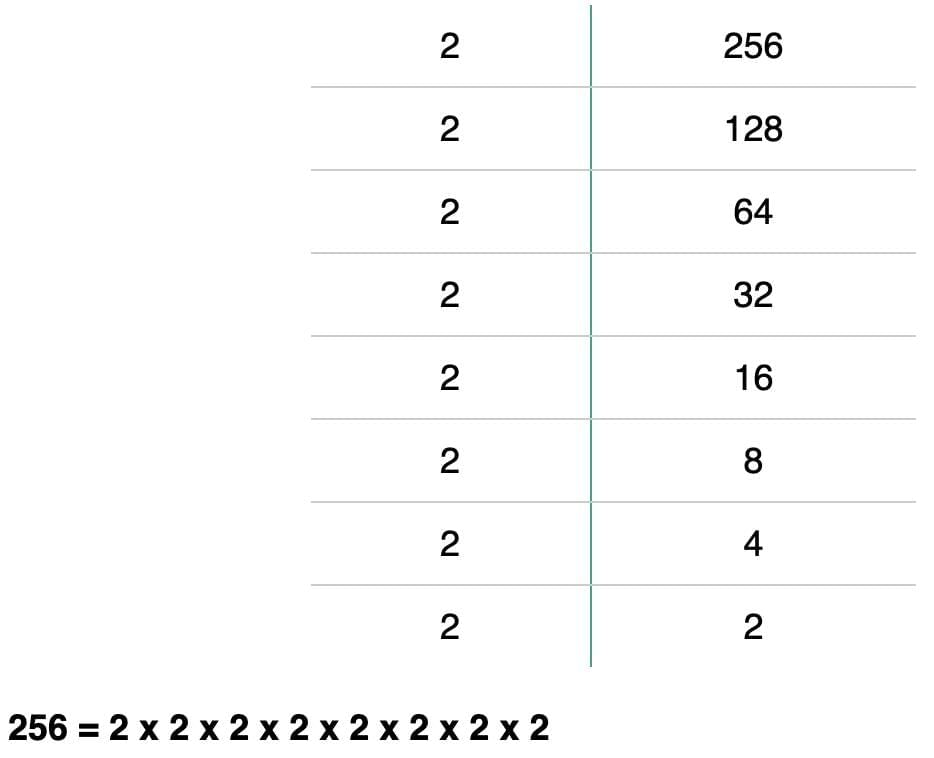 Example: 256 = 2⁸
Example: 256 = 2⁸  Estimation → use nearby perfect squares.
Estimation → use nearby perfect squares.
 Cubes grow faster than squares.
Cubes grow faster than squares. Other examples: 4104, 13832.
Other examples: 4104, 13832.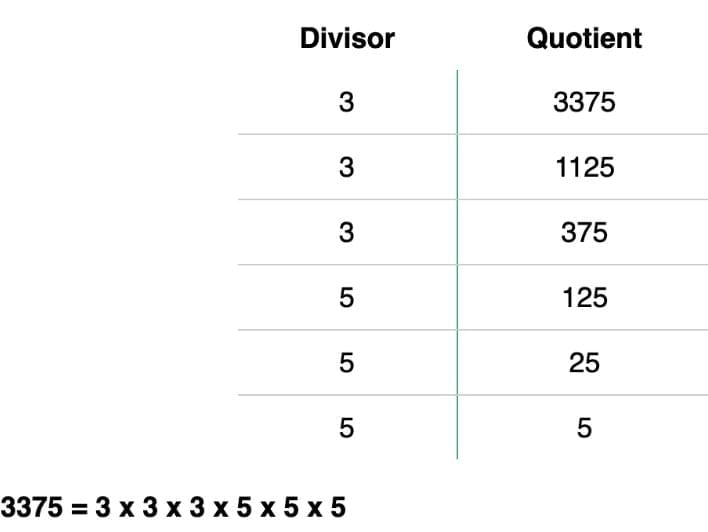 Example: 3375 = (3×3×3)(5×5×5) → ³√3375 = 15.
Example: 3375 = (3×3×3)(5×5×5) → ³√3375 = 15.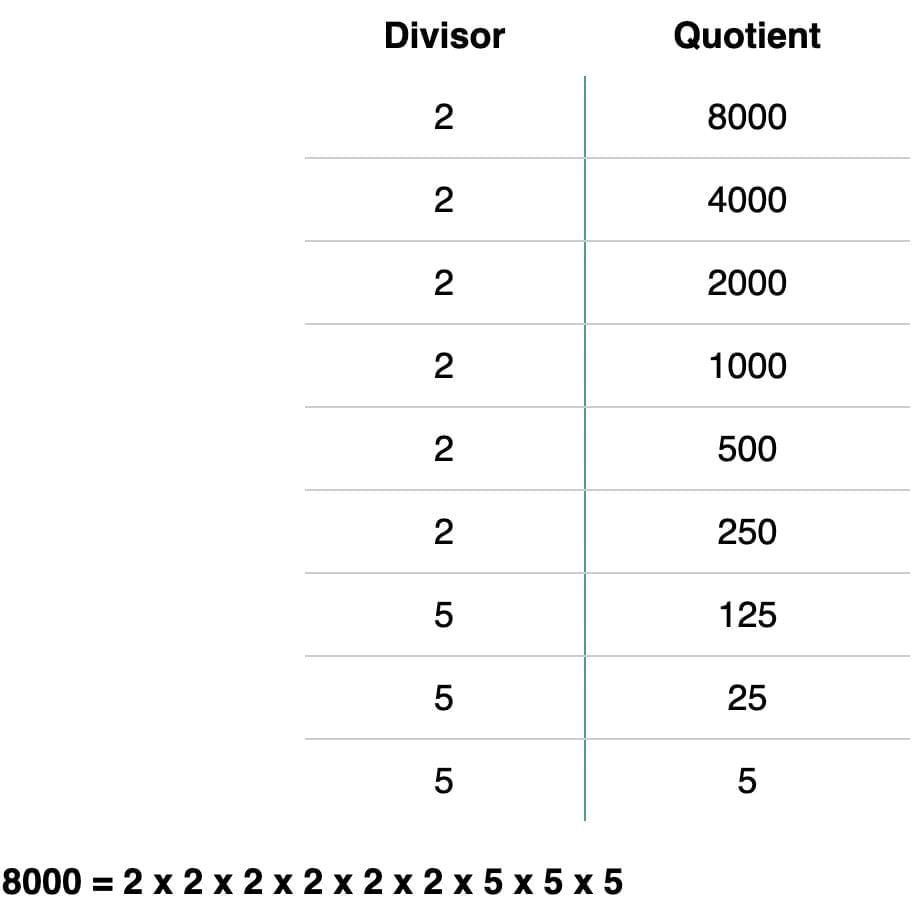 Example: ³√8000 = 20.8000 = (2×2×2) (2×2×2) (5×5×5)= 2×2×2 = 20.
Example: ³√8000 = 20.8000 = (2×2×2) (2×2×2) (5×5×5)= 2×2×2 = 20.