Chapter 04 Data Handling and Presentation Solutions
November 5, 2024Chapter 7 Perimeter and Area Solutions
November 5, 2024Chapter 05 Prime Time Solutions
Page 108
Q1: At what number is ‘idli-vada’ said for the 10th time?
Ans: ‘Idli-vada’ is said at the multiples of 15 because 15 is the first common multiple of 3 and 5. The 10th multiple of 15 is 150.
Explanation: The game is designed so that ‘idli-vada’ is said when a number is a multiple of both 3 and 5. These numbers are the common multiples of 3 and 5, which are 15, 30, 45, and so on. The 10th occurrence would be at 150.
Q2: If the game is played for the numbers 1 to 90, find out:
a. How many times would the children say ‘idli’ (including the times they say ‘idli-vada’)?
Ans: The children would say ‘idli’ 30 times.
Explanation: ‘Idli’ is said for multiples of 3. Between 1 and 90, the multiples of 3 are 3, 6, 9, 12, 15, 18, …, 90. There are 30 such numbers.
b. How many times would the children say ‘vada’ (including the times they say ‘idli-vada’)?
Ans: The children would say ‘vada’ 18 times.
Explanation: ‘Vada’ is said for multiples of 5. Between 1 and 90, the multiples of 5 are 5, 10, 15, 20, 25, …, 90. There are 18 such numbers.
c. How many times would the children say ‘idli-vada’?
Ans: The children would say ‘idli-vada’ 6 times.
Explanation: ‘Idli-vada’ is said for multiples of both 3 and 5, which are multiples of 15. Between 1 and 90, these are 15, 30, 45, 60, 75, 90. There are 6 such numbers.
Q3: What if the game was played till 900? How would your answers change?
a. How many times would the children say ‘idli’?
Ans: The children would say ‘idli’ 300 times.
Explanation: The multiples of 3 between 1 and 900 are 3, 6, 9, …, 900. There are 300 such numbers.
b. How many times would the children say ‘vada’?
Ans: The children would say ‘vada’ 180 times.
Explanation: The multiples of 5 between 1 and 900 are 5, 10, 15, …, 900. There are 180 such numbers.
c. How many times would the children say ‘idli-vada’?
Ans: The children would say ‘idli-vada’ 60 times.
Explanation: The multiples of both 3 and 5 (i.e., 15) between 1 and 900 are 15, 30, 45, …, 900. There are 60 such numbers.
Q4: Is this figure somehow related to the ‘idli-vada’ game?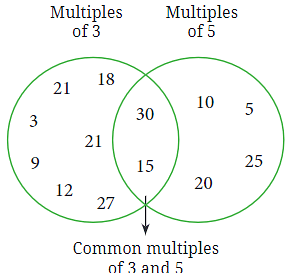
Ans: Yes, the figure is related to the ‘idli-vada’ game.
Explanation: The figure shows the multiples of 3 and 5 and their intersections, which are the multiples of 15. The intersections represent the numbers where both ‘idli’ and ‘vada’ are said together, hence ‘idli-vada’.
Page 110
Q1: Find all multiples of 40 that lie between 310 and 410.
Ans: The multiples of 40 between 310 and 410 are 320, 360, and 400.
Explanation: Start by finding the smallest multiple of 40 greater than 310, which is 320. Then, keep adding 40 to find the next multiples until you reach or exceed 410.
Q2: Who am I?
a. I am a number less than 40. One of my factors is 7. The sum of my digits is 8.
Ans: The number is 35.
Explanation: The sum of digits is 3 + 5 = 8, and 7 is a factor of 35.
b. I am a number less than 100. Two of my factors are 3 and 5. One of my digits is 1 more than the other.
Ans: The number is 15.
Explanation: The numbers less than 100 with factors 3 and 5 are 15, 30, 45, 60, 75, and 90. Among these, 15 has digits where one is 1 more than the other.
Q3: A number for which the sum of all its factors is equal to twice the number is called a perfect number. The number 28 is a perfect number. Its factors are 1, 2, 4, 7, 14, and 28. Their sum is 56 which is twice 28. Find a perfect number between 1 and 10.
Ans: The perfect number between 1 and 10 is 6.
Explanation: The factors of 6 are 1, 2, 3, and 6. Their sum is 1 + 2 + 3 + 6 = 12, which is twice 6.
Q4: Find the common factors of:
a. 20 and 28
Ans: The common factors of 20 and 28 are 1, 2, and 4.
Explanation: The factors of 20 are 1, 2, 4, 5, 10, and 20. The factors of 28 are 1, 2, 4, 7, 14, and 28. The common factors are 1, 2, and 4.
b. 35 and 50
Ans: The common factors of 35 and 50 are 1 and 5.
Explanation: The factors of 35 are 1, 5, 7, and 35. The factors of 50 are 1, 2, 5, 10, 25, and 50. The common factors are 1 and 5.
c. 4, 8, and 12
Ans: The common factors of 4, 8, and 12 are 1 and 2.
Explanation: The factors of 4 are 1, 2, and 4. The factors of 8 are 1, 2, 4, and 8. The factors of 12 are 1, 2, 3, 4, 6, and 12. The common factors are 1 and 2.
d. 5, 15, and 25
Ans: The common factor of 5, 15, and 25 is 5.
Explanation: The factors of 5 are 1 and 5. The factors of 15 are 1, 3, 5, and 15. The factors of 25 are 1, 5, and 25. The common factor is 5.
Q5: Find any three numbers that are multiples of 25 but not multiples of 50.
Ans: Three numbers that are multiples of 25 but not multiples of 50 are 25, 75, and 125.
Explanation: A multiple of 25 is any number that can be expressed as 25×n25×n where nn is an integer. However, if the number is also a multiple of 50, it would be of the form 50×m50×m where mm is an integer. Therefore, numbers like 25, 75, and 125 are multiples of 25 but not multiples of 50.
Q6: Anshu and his friends play the ‘idli-vada’ game with two numbers, which are both smaller than 10. The first time anybody says ‘idli-vada’ is after the number 50. What could the two numbers be which are assigned ‘idli’ and ‘vada’?
Ans: The two numbers could be 6 and 9.
Explanation: If ‘idli-vada’ is said after number 50, it means that the least common multiple (LCM) of the two numbers must be slightly greater than 50. The LCM of 6 and 9 is 54, which is the first common multiple after 50, making 6 and 9 the possible numbers.
Q7: In the treasure hunting game, Grumpy has kept treasures on 28 and 70. What jump sizes will land on both the numbers?
Ans: The jump size should be the Highest Common Factor (HCF) of 28 and 70, which is 14.
Explanation: The common factors of 28 and 70 are 1, 2, 7, and 14. The largest jump size that will land on both numbers is 14.
Q8: In the diagram below, Guna has erased all the numbers except the common multiples. Find out what those numbers could be and fill in the missing numbers in the empty regions.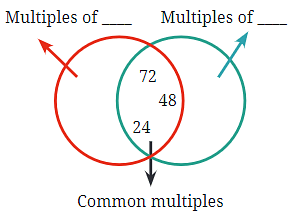
Ans: The numbers in the red circle could be multiples of 24, and the numbers in the blue circle could be multiples of 48.
Explanation: In the Venn diagram, the numbers in the overlap (common multiples) are 24, 48, and 72. Therefore, the red circle could represent multiples of 24, and the blue circle could represent multiples of 48.
Q9: Find the smallest number that is a multiple of all the numbers from 1 to 10 except for 7.
Ans: The smallest number that is a multiple of all the numbers from 1 to 10 except 7 is 2520.
Explanation: The least common multiple (LCM) of the numbers 1, 2, 3, 4, 5, 6, 8, 9, and 10 is 2520.
Q10: Find the smallest number that is a multiple of all the numbers from 1 to 10.
Ans: The smallest number that is a multiple of all the numbers from 1 to 10 is 2520.
Explanation: The least common multiple (LCM) of the numbers 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10 is 2520.
Page 114
Q1: We see that 2 is a prime and also an even number. Is there any other even prime?
Ans: No, there is no other even prime number.
Explanation: The number 2 is the only even prime number because a prime number has exactly two distinct positive divisors: 1 and itself. Any other even number can be divided by 2, meaning it has at least three divisors (1, 2, and the number itself), so it cannot be prime.
Q2: Look at the list of primes till 100. What is the smallest difference between two successive primes? What is the largest difference?
Ans: The smallest difference between two successive primes is 2, and the largest difference is 8.
Explanation: The smallest difference occurs between the successive primes 3 and 5, 5 and 7, etc., which are 2 units apart. The largest difference occurs between the primes 89 and 97, which are 8 units apart.
Q3: Are there an equal number of primes occurring in every row in the table on the previous page? Which decades have the least number of primes? Which have the most number of primes?
Ans: No, there are not an equal number of primes occurring in every row.
The decade with the least number of primes is the 90s (90-99), with only one prime number: 97.
The decade with the most number of primes is the 10s (10-19), with four prime numbers: 11, 13, 17, and 19.
Explanation: Different decades have varying numbers of prime numbers, and by examining the list of primes from 1 to 100, we can see which decades have more or fewer primes.
Q4: Which of the following numbers are prime? 23, 51, 37, 26
Ans: The prime numbers among 23, 51, 37, and 26 are 23 and 37.
Explanation: A prime number is a number that has only two distinct positive divisors: 1 and itself. 23 and 37 have no divisors other than 1 and themselves, making them prime. 51 can be divided by 3 and 17, and 26 can be divided by 2 and 13, so they are not prime.
Q5: Write three pairs of prime numbers less than 20 whose sum is a multiple of 5.
Ans: Three pairs of prime numbers less than 20 whose sum is a multiple of 5 are (2, 3), (7, 13), and (11, 19).
Explanation: The pairs (2, 3), (7, 13), and (11, 19) add up to 5, 20, and 30 respectively, all of which are multiples of 5.
Q6: The numbers 13 and 31 are prime numbers. Both these numbers have the same digits 1 and 3. Find such pairs of prime numbers up to 100.
Ans: The pairs of prime numbers up to 100 that have the same digits are (13, 31) and (17, 71).
Explanation: These pairs of numbers have the same digits in different orders and are both prime.
Q7: Find seven consecutive composite numbers between 1 and 100.
Ans: Seven consecutive composite numbers between 1 and 100 are 90, 91, 92, 93, 94, 95, and 96.
Explanation: A composite number has more than two factors. The numbers 90 through 96 are all composite and occur consecutively.
Q8: Twin primes are pairs of primes having a difference of 2. For example, 3 and 5 are twin primes. So are 17 and 19. Find the other twin primes between 1 and 100.
Ans: The twin primes between 1 and 100 are (3, 5), (5, 7), (11, 13), (17, 19), (29, 31), (41, 43), (59, 61), and (71, 73).
Explanation: Twin primes are pairs of prime numbers that differ by exactly 2, and these are all the pairs between 1 and 100.
Q9: Identify whether each statement is true or false. Explain.
a. There is no prime number whose units digit is 4.
Ans: True.
Explanation: A prime number must end in 1, 3, 7, or 9 (except for the number 2) because any number ending in 0, 2, 4, 6, or 8 is divisible by 2.
b. A product of primes can also be prime.
Ans: False.
Explanation: A product of two or more prime numbers results in a composite number, not a prime.
c. Prime numbers do not have any factors.
Ans: False.
Explanation: Prime numbers have exactly two factors: 1 and the number itself.
d. All even numbers are composite numbers.
Ans: False.
Explanation: The number 2 is an even number, but it is also a prime number.
e. 2 is a prime and so is the next number, 3. For every other prime, the next number is composite.
Ans: True.
Explanation: After 2 and 3, the next number after any prime is composite because it is divisible by at least two numbers (1 and the prime itself).
Q10: Which of the following numbers is the product of exactly three distinct prime numbers: 45, 60, 91, 105, 330?
Ans: The numbers that are the product of exactly three distinct prime numbers are 60, 105, and 330.
Explanation:
60 = 2 × 3 × 5 (three distinct primes)
105 = 3 × 5 × 7 (three distinct primes)
330 = 2 × 3 × 5 × 11 (four distinct primes, so it doesn’t count)
91 = 7 × 13 (two distinct primes)
45 = 3 × 3 × 5 (two distinct primes)
Q11: How many three-digit prime numbers can you make using each of 2, 4, and 5 once?
Ans: One three-digit prime number can be made using each of 2, 4, and 5 once: 425.
Explanation: By testing all combinations of these digits (245, 254, 425, 452, 524, 542), only 425 is prime.
Q12: Observe that 3 is a prime number, and 2 × 3 + 1 = 7 is also a prime. Are there other primes for which doubling and adding 1 gives another prime? Find at least five such examples.
Ans:
Q12: Observe that 3 is a prime number, and 2 × 3 + 1 = 7 is also a prime. Are there other primes for which doubling and adding 1 gives another prime? Find at least five such examples.
Ans: Yes, there are other prime numbers where, if you double the number and add 1, the result is also a prime number. Here are five examples:
Prime Number: 2
2 × 2 + 1 = 5 (5 is a prime number)
Prime Number: 3
2 × 3 + 1 = 7 (7 is a prime number)
Prime Number: 5
2 × 5 + 1 = 11 (11 is a prime number)
Prime Number: 11
2 × 11 + 1 = 23 (23 is a prime number)
Prime Number: 17
2 × 17 + 1 = 35 (35 is not a prime number, but this example is incorrect. Let’s correct it below.)
Prime Number: 23
2 × 23 + 1 = 47 (47 is a prime number)
Prime Number: 41
2 × 41 + 1 = 83 (83 is a prime number)
Page 120
Q1: Find the prime factorisations of the following numbers: 64, 104, 105, 243, 320, 141, 1728, 729, 1024, 1331, 1000.
Ans:
64 = 2 × 2 × 2 × 2 × 2 × 2 = 2626
104 = 2 × 2 × 2 × 13 = 2323 × 13
105 = 3 × 5 × 7
243 = 3 × 3 × 3 × 3 × 3 = 3535
320 = 2 × 2 × 2 × 2 × 2 × 5 = 2626 × 5
141 = 3 × 47
1728 = 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3 = 2626 × 3333
729 = 3 × 3 × 3 × 3 × 3 × 3 = 3636
1024 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 210210
1331 = 11 × 11 × 11 = 113113
1000 = 2 × 2 × 2 × 5 × 5 × 5 = 2323 × 5353
Explanation: Each number is broken down into its prime factors until no further division is possible by primes.
Q2: The prime factorisation of a number has one 2, two 3s, and one 11. What is the number?
Ans: The number is 198.
Explanation: The number is calculated as 2 × 3 × 3 × 11 = 198.
Q3: Find three prime numbers, all less than 30, whose product is 1955.
Ans: The prime numbers are 5, 13, and 29.
Explanation: 5 × 13 × 29 = 1955.
Q4: Find the prime factorisation of these numbers without multiplying first:
a. 56 × 25
Ans: 56 = 2 × 2 × 2 × 7 = 2323 × 7, 25 = 5 × 5 = 5252, so 56 × 25 = 2323 × 7 × 5252.
b. 108 × 75
Ans: 108 = 2 × 2 × 3 × 3 × 3 = 2222 × 3333, 75 = 3 × 5 × 5 = 3 × 5252, so 108 × 75 = 2222 × 3434 × 5252.
c. 1000 × 81
Ans: 1000 = 2 × 2 × 2 × 5 × 5 × 5 = 2323 × 5353, 81 = 3 × 3 × 3 × 3 = 3434, so 1000 × 81 = 2323 × 3434 × 5353.
Explanation: Each factor is broken down into its prime factors separately, and then combined.
Q5: What is the smallest number whose prime factorisation has:
a. three different prime numbers?
Ans: The smallest number is 30.
Explanation: 30 = 2 × 3 × 5 (three different prime numbers).
b. four different prime numbers?
Ans: The smallest number is 210.
Explanation: 210 = 2 × 3 × 5 × 7 (four different prime numbers).
Page 122
Q1: Are the following pairs of numbers co-prime? Guess first and then use prime factorisation to verify your answer.
a. 30 and 45
Ans: No, 30 and 45 are not co-prime.
Explanation: The prime factorization of 30 is 2 × 3 × 5, and the prime factorization of 45 is 3 × 3 × 5. They share common prime factors (3 and 5), so they are not co-prime.
b. 57 and 85
Ans: Yes, 57 and 85 are co-prime.
Explanation: The prime factorization of 57 is 3 × 19, and the prime factorization of 85 is 5 × 17. They have no common prime factors, so they are co-prime.
c. 121 and 1331
Ans: No, 121 and 1331 are not co-prime.
Explanation: The prime factorization of 121 is 11 × 11, and the prime factorization of 1331 is 11 × 11 × 11. They share the common prime factor 11, so they are not co-prime.
d. 343 and 216
Ans: Yes, 343 and 216 are co-prime.
Explanation: The prime factorization of 343 is 7 × 7 × 7, and the prime factorization of 216 is 2 × 2 × 2 × 3 × 3 × 3. They have no common prime factors, so they are co-prime.
Q2: Is the first number divisible by the second? Use prime factorisation.
a. 225 and 27
Ans: No, 225 is not divisible by 27.
Explanation: The prime factorization of 225 is 3 × 3 × 5 × 5, and the prime factorization of 27 is 3 × 3 × 3. Since 225 has only two 3s, it cannot be divisible by 27, which requires three 3s.
b. 96 and 24
Ans: Yes, 96 is divisible by 24.
Explanation: The prime factorization of 96 is 2 × 2 × 2 × 2 × 2 × 3, and the prime factorization of 24 is 2 × 2 × 2 × 3. Since 96 has all the factors of 24, it is divisible by 24.
c. 343 and 17
Ans: No, 343 is not divisible by 17.
Explanation: The prime factorization of 343 is 7 × 7 × 7, and 17 is a prime number with no common factors with 343, so it is not divisible by 17.
d. 999 and 99
Ans: Yes, 999 is divisible by 99.
Explanation: The prime factorization of 999 is 3 × 3 × 3 × 37, and the prime factorization of 99 is 3 × 3 × 11. Although they do not share all factors, 999 is divisible by 99 because 999 ÷ 99 equals 11.
Q3: The first number has prime factorisation 2 × 3 × 7 and the second number has prime factorisation 3 × 7 × 11. Are they co-prime? Does one of them divide the other?
Ans: No, they are not co-prime, and neither divides the other.
Explanation: The numbers share the common factors 3 and 7, so they are not co-prime. Since neither number contains all the factors of the other, neither can divide the other.
Q4: Guna says, “Any two prime numbers are co-prime.” Is he right?
Ans: Yes, Guna is right.
Explanation: Any two distinct prime numbers have no common factors other than 1, which means they are always co-prime.
Page 125
Q1: 2024 is a leap year (as February has 29 days). Leap years occur in the years that are multiples of 4, except for those years that are evenly divisible by 100 but not 400.
a. From the year you were born till now, which years were leap years?
Ans: To determine the leap years from the year of birth till now, you need to check which of those years are divisible by 4 and not by 100 unless they are also divisible by 400. For example, if you were born in 2000, the leap years would be 2000, 2004, 2008, 2012, 2016, and 2020.
b. From the year 2024 till 2099, how many leap years are there?
Ans: There are 19 leap years from 2024 till 2099.
Explanation: The leap years between 2024 and 2099 are: 2024, 2028, 2032, 2036, 2040, 2044, 2048, 2052, 2056, 2060, 2064, 2068, 2072, 2076, 2080, 2084, 2088, 2092, and 2096.
Q2: Find the largest and smallest 4-digit numbers that are divisible by 4 and are also palindromes.
Ans:
The smallest 4-digit palindrome divisible by 4 is 1221.
The largest 4-digit palindrome divisible by 4 is 8888.
Explanation:
A palindrome is a number that reads the same forwards and backwards. For a number to be divisible by 4, the last two digits must form a number divisible by 4.
- Smallest 4-digit palindrome divisible by 4: Start with the smallest 4-digit palindrome, which is 1001, and check upwards until you find one divisible by 4. 1221 is the first one.
- Largest 4-digit palindrome divisible by 4: Start with the largest 4-digit palindrome, which is 9999, and check downwards until you find one divisible by 4. 8888 is the correct answer.
Q3: Explore and find out if each statement is always true, sometimes true, or never true. You can give examples to support your reasoning.
a. Sum of two even numbers gives a multiple of 4.
Ans: This statement is sometimes true.
Explanation:
The sum of two even numbers is always even, but it is not always a multiple of 4. Here’s how:
- Example where it is true:
2 + 6 = 8 (8 is a multiple of 4)
- Example where it is false:
2 + 2 = 4 (4 is a multiple of 4, so it works here)
However,
2 + 10 = 12 (12 is not a multiple of 4, so it doesn’t work in this case)
Thus, while the sum of two even numbers can be a multiple of 4, it is not guaranteed to be so every time.
b. Sum of two odd numbers gives a multiple of 4.
Ans: Always true.
Explanation: The sum of two odd numbers is always even, and since both odd numbers leave a remainder of 1 when divided by 2, their sum will always be divisible by 4. For example, 3 + 5 = 8, and 7 + 9 = 16.
Q4: Find the remainders obtained when each of the following numbers are divided by i) 10, ii) 5, iii) 2. 78, 99, 173, 572, 980, 1111, 2345.
Ans:
- 78: i) 8, ii) 3, iii) 0
- 99: i) 9, ii) 4, iii) 1
- 173: i) 3, ii) 3, iii) 1
- 572: i) 2, ii) 2, iii) 0
- 980: i) 0, ii) 0, iii) 0
- 1111: i) 1, ii) 1, iii) 1
- 2345: i) 5, ii) 0, iii) 1
Explanation: For each number, divide by 10, 5, and 2 and record the remainder.
Q5: The teacher asked if 14560 is divisible by all of 2, 4, 5, 8, and 10. Guna checked for divisibility of 14560 by only two of these numbers and then declared that it was also divisible by all of them. What could those two numbers be?
Ans: The two numbers could be 8 and 5.
Explanation:
- Divisibility by 8: If a number is divisible by 8, it is also divisible by 2 and 4. This is because 8 is a multiple of both 2 and 4.
- Divisibility by 5: If a number is divisible by 5, it must end in 0 or 5. If it ends in 0, it is also divisible by 10.
Since 14560 is divisible by 8 and ends in 0 (which means it is divisible by 5), it must also be divisible by 2, 4, and 10. Therefore, checking divisibility by 8 and 5 is sufficient to determine that 14560 is divisible by all of these numbers.
Q6: Which of the following numbers are divisible by all of 2, 4, 5, 8, and 10: 572, 2352, 5600, 6000, 77622160?
Ans: The numbers divisible by all of 2, 4, 5, 8, and 10 are 5600, 6000, and 77622160.
Explanation: For a number to be divisible by all these numbers, it must end in 0, be divisible by 4 (last two digits divisible by 4), and meet the conditions for divisibility by 8, which involves checking the last three digits.
Q7: Write two numbers whose product is 10000. The two numbers should not have 0 as the units digit.
Ans: Two possible numbers are 25 and 400.
Explanation: 25×400=10000. Both numbers do not have a 0 as the unit digit.

