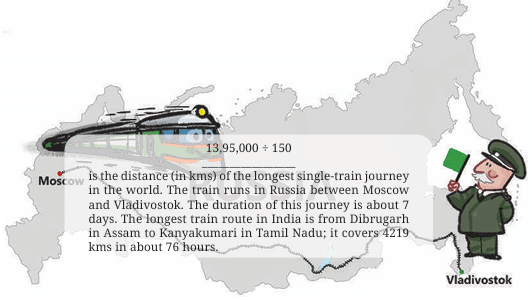
Multiplication of Fractions
Multiplication involving fractions can arise in various scenarios, such as finding a part of a whole or scaling quantities.
We begin by examining the multiplication of a fraction by a whole number.
Consider a situation where we need to find the total distance covered if someone walks a certain fractional distance multiple times.

For instance, if Aaron walks 3 kilometres in 1 hour, how far can he walk in 5 hours?
This is a simple multiplication of whole numbers: 5 hours × 3 km/hour = 15 km. The calculation involves repeated addition: 3 + 3 + 3 + 3 + 3 = 15 km.
Now, let’s adapt this to fractions.
Suppose Aaron’s pet tortoise walks only 1/4 kilometre in 1 hour. How far can it walk in 3 hours?
The distance covered is a fraction, but the principle remains the same: multiplication.
We need to calculate 3 × (1/4) km.
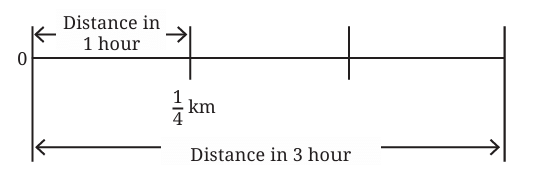
Visually, we can represent this as adding 1/4 three times: 1/4 + 1/4 + 1/4.
Since the denominators are the same, we add the numerators: (1+1+1)/4 = 3/4.
Therefore, the tortoise walks 3/4 kilometre in 3 hours.
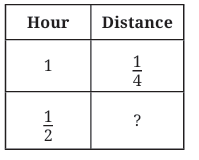
Now, we need to figure out how far Aaron can walk in a fraction of an hour, for example, in 1/5 of an hour and 2/5 of an hour.
How Do We Calculate Distance in Fractional Time?
When the time is a fraction of an hour, like 1/5 or 2/5 of an hour, we calculate the distance by multiplying the fraction by the distance Aaron covers in 1 full hour.
1. How Far Can Aaron Walk in 1/5 of an Hour?
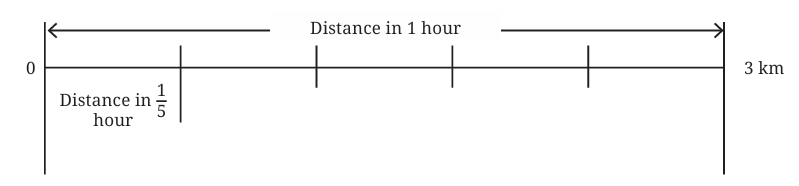
We know that in 1 hour, Aaron walks 3 kilometers.
To find out how far Aaron can walk in 1/5 hour, we multiply:
=15×3km
This means we need to divide 3 kilometers into 5 equal parts because the time is 1/5 of an hour.
Step-by-Step:
- Divide 3 kilometers by 5 to get the distance Aaron walks in 1/5 of an hour.
35=0.653 = 0.6 km
So, Aaron can walk 0.6 kilometers in 1/5 of an hour.
2. How Far Can Aaron Walk in 2/5 of an Hour?
Now, let’s figure out how far Aaron can walk in 2/5 of an hour.
We know that in 1 hour, Aaron walks 3 kilometers.
To find out how far Aaron can walk in 2/5 of an hour, we multiply:
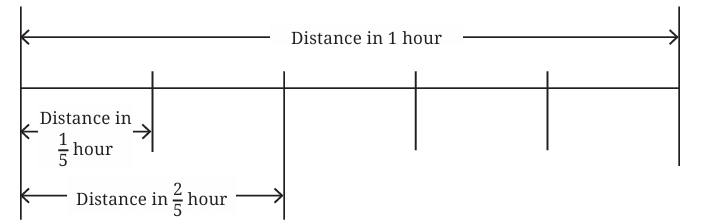
=25×3km
This means we need to find the distance covered in 1/5 of an hour first, and then multiply that by 2 (since 2/5 is double 1/5).
Step-by-Step:
- First, calculate the distance Aaron covers in 1/5 of an hour. We already know from the previous part that in 1/5 of an hour, Aaron covers 0.6 kilometers.
- Now, multiply the result by 2 (since we need to find the distance in 2/5 of an hour):
2×0.6=1.2 km
So, Aaron can walk 1.2 kilometers in 2/5 of an hour.
Discussion
We did this multiplication as follows:
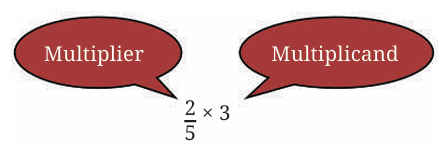
First, we divided the multiplicand, 3 , by the denominator of the multiplier, 5, to get 3/5.
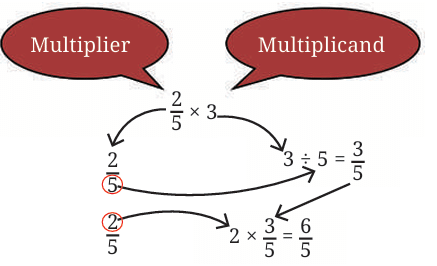
We then multiplied the result by the numerator of the multiplier, that is 2, to get 6 /5 . Thus, whenever we need to multiply a fraction and a whole number, we follow the steps above.
Multiplying Two Fractions
We know, that Aaron’s pet tortoise can walk only 1/4 km in 1 hour. How far can it walk in half an hour?
Following our approach of using multiplication to solve such problems, we have, Distance covered in 1/2 hour = 1/2 × 1/4 km.
Finding the product:
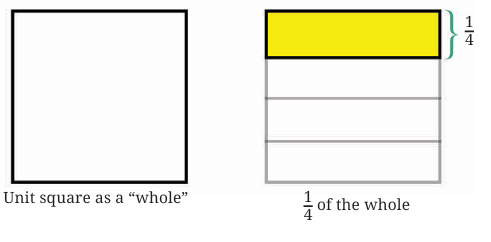
Imagine a whole unit, say a square. First, divide it into four equal vertical strips; one strip represents 1/4.
Now, we need to find half of this shaded 1/4. We can do this by dividing the entire square horizontally into two equal parts.
The portion that is both shaded (part of the original 1/4) and falls within the bottom half represents (1/2) × (1/4).
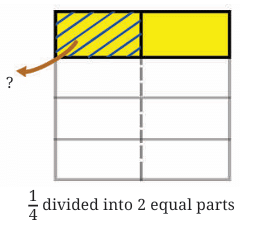
Since the whole is divided into 8 equal parts and one of the parts is shaded, we can say that 1/ 8 of the whole is shaded. So, the distance covered by the tortoise in half an hour is 1/ 8 km.
This tells us that 1/2 × 1/4 = 1/8 .
Example: If the tortoise walks faster and it can cover 2/ 5 km in 1 hour, how far will it walk in 3/ 4 of an hour?
Sol: We want to calculate the distance covered in 3/4 of an hour, which can be written as:
=34×25
Now, let’s break this problem into two smaller parts to make it easier to understand:
Since the tortoise covers 2/5 km in 1 hour, we first need to find out how much it walks in 1/4 of an hour (since 3/4 of an hour is 3 times 1/4 of an hour).
To find the distance in 1/4 of an hour, we need to divide 2/5 km into 4 equal parts (because we are looking for the distance in just 1/4 of an hour).
How to divide 2/5 into 4 equal parts:
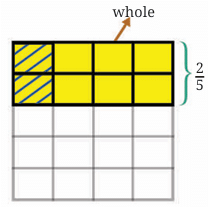 Start with the distance the tortoise covers in 1 hour: 2/5 km.
Start with the distance the tortoise covers in 1 hour: 2/5 km.- How much of the whole is it?
The whole is divided into 5 rows and 4 columns, creating 5 × 4 = 20 equal parts. Number of these parts shaded = 2.
So, the distance covered in 1/ 4 of an hour = 2/ 20 .

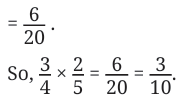
Now, we need to multiply 2/ 20 by 3. Distance covered in 3/ 4 of an hour =
Try yourself:If Aaron walks at a speed of 3 kilometers per hour, how far can he walk in 1/5 of an hour?
- A.0.6 kilometers
- B.1.2 kilometers
- C.1.0 kilometers
- D.0.8 kilometers
View Solution
Connection between the Area of a Rectangle and Fraction Multiplication
We are given a unit square with side length 1 unit. A rectangle is drawn inside the unit square. The length and breadth of the rectangle are both fractions:
- Length = 1/2 unit
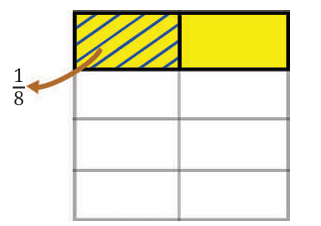 Breadth = 1/4 unit
Breadth = 1/4 unit
We need to calculate the area of this rectangle, and also understand the relationship between the product of the length and breadth and the area of the rectangle.
The area of any rectangle can be found by multiplying its length by its breadth.
So, the area of the rectangle is:
=12×14
To multiply fractions, we multiply the numerators together and the denominators together:
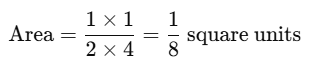
So, the area of the rectangle is 1/8 square units.
This means that the area of the rectangle is the product of the length and breadth of the rectangle, even when they are fractions.
Let us find the product by observing what we did in the above cases.
In each case, the whole is divided into rows and columns. The number of rows is the denominator of the multiplicand, which is 18 in this case. The number of columns is the denominator of the multiplier, which is 12 in this case.
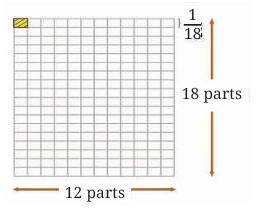
Thus, the whole is divided into 18 × 12 equal parts.
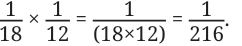
So,
Thus, when two fractional units are multiplied, their product is
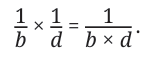
We express this as:
Multiplying Numerators and Denominators
When you multiply two fractions, you multiply the numerators (the top numbers) together, and the denominators (the bottom numbers) together.
In the example below:
- We are multiplying 5/12 by 7/18.
- First, you multiply the numerators:
5×7=35. 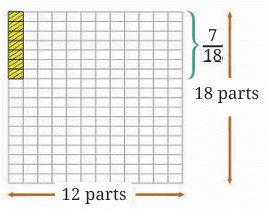 Then, you multiply the denominators:
Then, you multiply the denominators:
12×18=216.
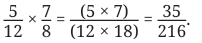
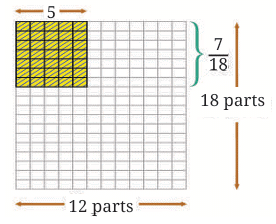
So, the result of multiplying these fractions is:
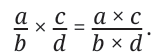
The rule you are learning here is that when you multiply fractions, the product is:
This formula was first stated in this general form by Brahmagupta in his Brāhmasphuṭasiddhānta in 628 CE.
Whole Numbers as Fractions
If you are multiplying a fraction by a whole number, you can turn the whole number into a fraction by giving it a denominator of 1.
For example:
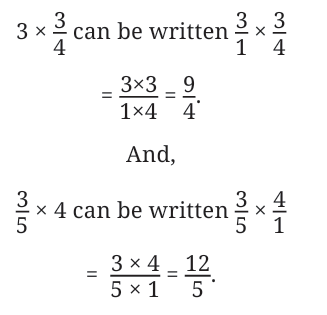
Multiplication of Fractions — Simplifying to Lowest Form
- Multiply the following fractions and express the product in its lowest form:
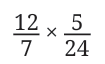
- Instead of multiplying the numerators (12 and 5) and denominators (7 and 24) first and then simplifying, we could do the following:
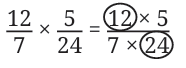
We see that both the circled numbers have a common factor of 12. We know that a fraction remains the same when the numerator and denominator are divided by the common factor. In this case, we can divide them by 12.
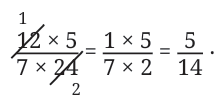
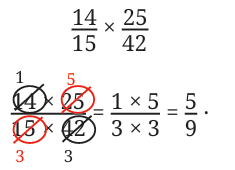
Let us use the same technique to do one more multiplication.

When multiplying fractions, we can first divide the numerator and denominator by their common factors before multiplying the numerators and denominators. This is called cancelling the common factors.
Is the Product Always Greater than the Numbers Multiplied?
Since, we know that when a number is multiplied by 1, the product remains unchanged, we will look at multiplying pairs of numbers where neither of them is 1. When we multiply two counting numbers greater than 1, say 3 and 5, the product is greater than both the numbers being multiplied.
3 × 5 = 15
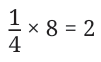
The product, 15, is more than both 3 and 5. But what happens when we multiply 1 /4 and 8?
In the above multiplication the product, 2, is greater than 1/4 , but less than 8.
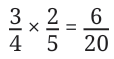
What happens when we multiply 3/4 and 2/5 ?
Let us compare this product 6/20 with the numbers 3/4 and 2/5 . For this,
let us express 3 /4 as 15/ 20 and 2 /5 as 8/ 20 . From this we can see that the product is less than both the numbers.
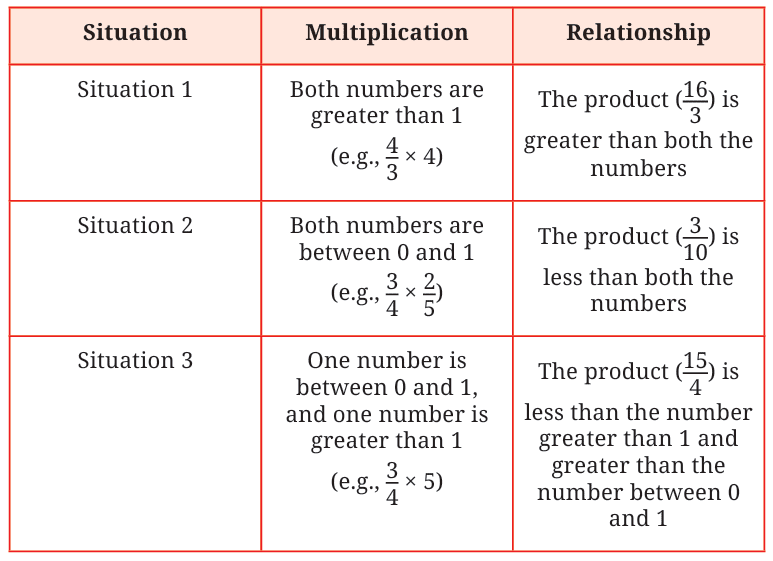
Order of Multiplication
Just like with whole numbers, the order in which we multiply fractions does not affect the result (commutative property).
(a/b) × (c/d) = (c/d) × (a/b).
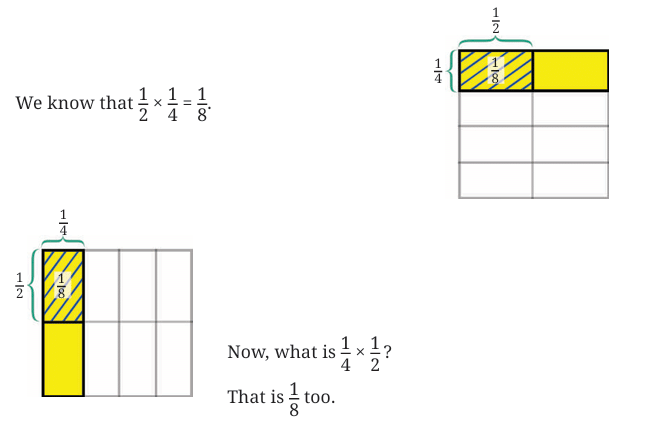
For example,
Division of Fractions
When you’re dividing fractions, it might look tricky at first, but we can turn it into a multiplication problem, which is easier to handle. Here’s how you do it.
The Idea Behind Division:
First, think about regular division. For example:
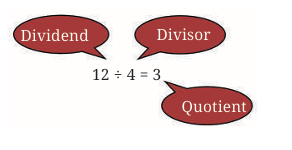
12÷4=3
You can also think about it this way:
What number times 4 equals 12?
4×3=12
This is how we can think of division as multiplication: you find out what number you need to multiply by the divisor to get the dividend.
Now, Let’s Do the Same with Fractions:
When we divide fractions, we’ll use the same idea. Instead of dividing directly, we turn it into a multiplication problem by using the reciprocal of the second fraction.
Example 1:
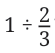
Let’s try this:
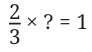
Let us rewrite this as a multiplication problem
What should be multiplied by 2/3 to get the product 1?
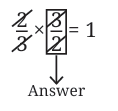
If we somehow cancel out the 2 and the 3, we are left with 1.
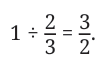
So,

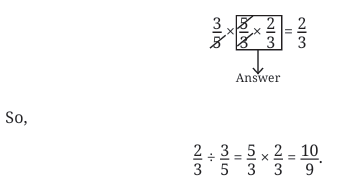
Let us try another problem:
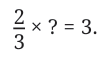
This is the same as
Can you find the answer?
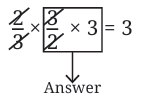
We know what to multiply 2/3 by to get 1. We just need to multiply that by 3 to get 3. So,
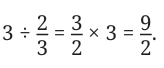
So,
What is 1/5 ÷ 1/2 ?
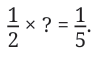
Rewriting it as a multiplication problem, we have
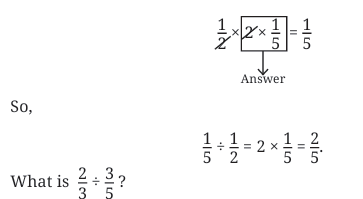
How do we solve this?

Rearranging this as multiplication, we have
How will we solve this?
Try yourself:
What is the area of a rectangle with length 1/2 unit and breadth 1/4 unit?
- A.1 square unit
- B.1/4 square units
- C.1/2 square units
- D.1/8 square units
View Solution
Discussion
The process of dividing by a fraction is equivalent to multiplying by its reciprocal. This rule applies whether you are dividing a whole number by a fraction, a fraction by a whole number, or a fraction by another fraction.
Rule: a ÷ (c/d) = a × (d/c)
Rule: (a/b) ÷ c = (a/b) ÷ (c/1) = (a/b) × (1/c) = a / (b × c)
Rule: (a/b) ÷ (c/d) = (a/b) × (d/c) = (a × d) / (b × c)
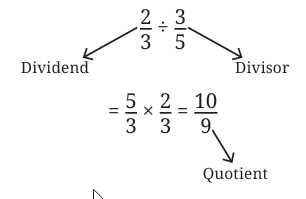
Dividend, Divisor and the Quotient
When dividing positive numbers:
- If the divisor is a proper fraction (between 0 and 1), the quotient will be greater than the dividend. Example: 5 ÷ (1/2) = 5 × 2 = 10. Here, 10 > 5.
- If the divisor is an improper fraction (greater than 1), the quotient will be less than the dividend. Example: 5 ÷ (3/2) = 5 × (2/3) = 10/3 (approx 3.33). Here, 10/3 < 5.
This makes sense because dividing by a number less than 1 means finding out how many times that small piece fits into the dividend, resulting in a larger number.
Dividing by a number greater than 1 means splitting the dividend into larger chunks, resulting in a smaller number of chunks.
Some Problems Involving Fractions
This section applies the concepts of fraction multiplication and division to solve practical word problems.
Example: Leena made 5 cups of tea and used a total of 1/4 litre of milk. How much milk is there in each cup of tea, assuming it was distributed equally?
Sol: To find the amount of milk per cup, we need to divide the total amount of milk (1/4 litre) by the number of cups (5). Calculation: (1/4) ÷ 5
Using the rule for division (multiply by the reciprocal): (1/4) ÷ 5 = (1/4) ÷ (5/1) = (1/4) × (1/5) Multiply numerators and denominators: (1 × 1) / (4 × 5) = 1/20.
So, each cup of tea has 1/20 litre of milk.

Example: Some of the oldest examples of working with non-unit fractions occur in humanity’s oldest geometry texts, the Śhulbasūtra. Here is an example from Baudhāyana’s Śhulbasūtra (c. 800 BCE).
Cover an area of 7 ½ square units with square bricks, each having sides of 1/5 units. How many such square bricks are needed?
Sol: First, find the area of one square brick: Area = side × side = (1/5) × (1/5) = 1/25 square units.
Next, convert the total area to an improper fraction: 7 ½ = (7 × 2 + 1) / 2 = 15/2 square units.
To find the number of bricks, divide the total area by the area of one brick: Number of bricks = (Total Area) ÷ (Area of one brick) Number of bricks = (15/2) ÷ (1/25)
Using the rule for division (multiply by the reciprocal):
Number of bricks = (15/2) × (25/1)
Multiply numerators and denominators:
(15 × 25) / (2 × 1) = 375 / 2.
Example: This problem is from Chaturveda Prithudakasvami’s commentary (c. 860 CE) on Brahmagupta’s work.
Four fountains fill a cistern. The first fills it in a day (rate = 1 cistern/day). The second fills it in half a day (rate = 1 ÷ (1/2) = 2 cisterns/day). The third fills it in a quarter of a day (rate = 1 ÷ (1/4) = 4 cisterns/day). The fourth fills it in one-fifth of a day (rate = 1 ÷ (1/5) = 5 cisterns/day).
If they all flow together, how much time will they take to fill the cistern?
Sol: First, find the combined rate by adding the individual rates: Combined Rate = Rate1 + Rate2 + Rate3 + Rate4 Combined Rate = 1 + 2 + 4 + 5 = 12 cisterns/day.
This means together, the fountains fill 12 cisterns in one day. To find the time to fill one cistern, we take the reciprocal of the combined rate: Time = 1 / (Combined Rate) Time = 1 / 12 days.
So, together, the four fountains will fill the cistern in 1/12 of a day.
Fractional Relations
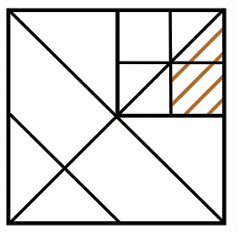
In the image, we have a square with lines drawn inside it, and part of the square is shaded. The problem asks, “What fraction of the whole square does the shaded region occupy?”
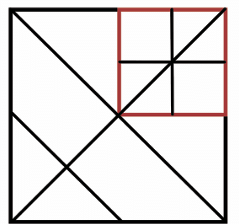
To solve this, the idea is to divide the whole square into smaller, manageable parts and use these smaller parts to calculate the fraction of the area taken by the shaded region.
Now, the top right square is colored red. It occupies 1/4 of the area of the whole square. This is because the entire square is divided into four equal smaller squares, and the red square is one of them. So, if the whole square is considered to have an area of 1 square unit, the area of the red square is 1/4 of that.

Now, A yellow triangle inside the red square. We are told that the yellow triangle occupies half of the red square’s area. So, the area of the yellow triangle is:
12×14=18 of the whole square.
Now, the yellow triangle is shaded. The shaded region inside the yellow triangle occupies 3/4 of the area of the triangle. So, the shaded area in the triangle is:
34×18=332 of the whole square.
A Dramma-tic Donation
A Dramma-tic Donation (from Līlāvatī): “O wise one! A miser gave to a beggar 1/5 of 1/16 of 1/4 of 1/2 of 2/3 of 3/4 of a dramma. If you know the mathematics of fractions well, tell me O child, how many cowrie shells were given by the miser to the beggar?”
A dramma was a silver coin. 1 dramma = 1280 cowrie shells (the lowest value coin).
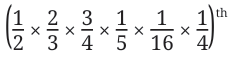
Fraction given = part of a dramma.
Evaluating it gives 6 / 7680.
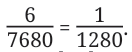
Upon simplifying to its lowest form, we get
So, one cowrie shell was given to the beggar.
You can see in the answer Bhāskarāchārya’s humour! The miser had given the beggar only one coin of the least value (cowrie).
Around the 12th century, several types of coins were in use in different kingdoms of the Indian subcontinent. Most commonly used were gold coins (called dinars/gadyanas and hunas), silver coins (called drammas/tankas), copper coins (called kasus/panas and mashakas), and cowrie shells. The exact conversion rates between these coins varied depending on the region, time period, economic conditions, weights of coins and their purity.
Gold coins had high value and were used in large transactions and to store wealth. Silver coins were more commonly used in everyday transactions. Copper coins had low value and were used in smaller transactions. Cowrie shells were the lowest denomination and were used in very small transactions and as change.
If we assume:
1 gold dinar = 12 silver drammas
1 silver dramma = 4 copper panas
1 copper pana = 30 cowrie shells
Then:
1 cowrie shell = 1/30 copper pana
1 copper pana = 1/(12 × 4) = 1/48 gold dinar
Therefore,
1 cowrie shell = 1/30 × 1/48 = 1/1440 gold dinar
A Pinch of History
Fractions have played a crucial role throughout history, particularly in problems involving sharing and dividing quantities. The general concept of non-unit fractions and their arithmetic operations (addition, subtraction, multiplication, division) developed significantly in India.
- Ancient Texts (Shulbasutra, c. 800 BCE): These texts, concerned with constructing fire altars for rituals, used general non-unit fractions extensively, including performing division as seen in Example 4.
- Early Commonplace Use (c. 150 BCE): Evidence suggests fractions became common in popular culture, indicated by references to reducing fractions to lowest terms (apavartana) in the philosophical work of the Jain scholar Umasvati.
- Codification by Brahmagupta (c. 628 CE): General rules for arithmetic operations on fractions, similar to modern methods, were first codified by Brahmagupta in his work Brahmasphutasiddhanta.
- Multiplication: “Multiplication of two or more fractions is obtained by taking the product of the numerators divided by the product of the denominators.” (Verse 12.1.3).
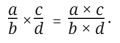
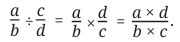 Division: “The division of fractions is performed by interchanging the numerator and denominator of the divisor; the numerator of the dividend is then multiplied by the (new) numerator, and the denominator by the (new) denominator.”
Division: “The division of fractions is performed by interchanging the numerator and denominator of the divisor; the numerator of the dividend is then multiplied by the (new) numerator, and the denominator by the (new) denominator.”
- Clarification by Bhaskara II (Līlāvatī, c. 1150 CE): Bhaskara II further clarified Brahmagupta’s statement on division using the explicit notion of the reciprocal: “Division of one fraction by another is equivalent to multiplication of the first fraction by the reciprocal of the second.” (Verse 2.3.40).
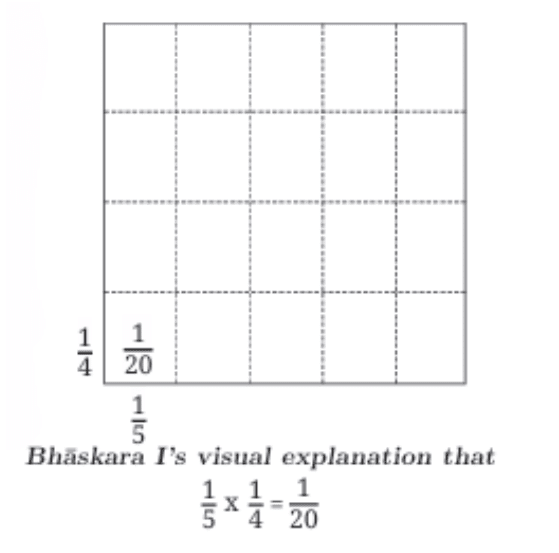
- Geometric Interpretations (Bhaskara I, c. 629 CE): In his commentary on Aryabhata’s work, Bhaskara I described geometric interpretations of fraction multiplication and division using the division of a square into rectangles (similar to the area model discussed earlier).
 Other Indian Mathematicians: Many others like Shridharacharya (c. 750 CE), Mahaviracharya (c. 850 CE), Caturveda Prithudakasvami (c. 860 CE), and Bhaskara II further developed the use of arithmetic fractions.
Other Indian Mathematicians: Many others like Shridharacharya (c. 750 CE), Mahaviracharya (c. 850 CE), Caturveda Prithudakasvami (c. 860 CE), and Bhaskara II further developed the use of arithmetic fractions.- Transmission: The Indian theory of fractions and arithmetic operations was transmitted to and developed further by Arab and African mathematicians (like al-Hassar, c. 1192 CE, Morocco). It was then transmitted to Europe via the Arabs over subsequent centuries, coming into general use around the 17th century and becoming indispensable in modern mathematics.

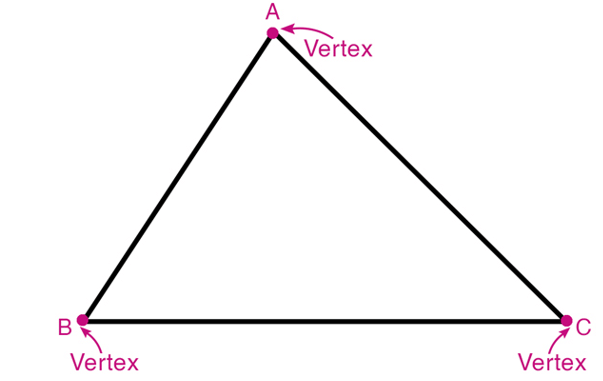 Three Vertices: These are the corner points where the sides intersect. Think of them as the ‘tips’ of the triangle.
Three Vertices: These are the corner points where the sides intersect. Think of them as the ‘tips’ of the triangle.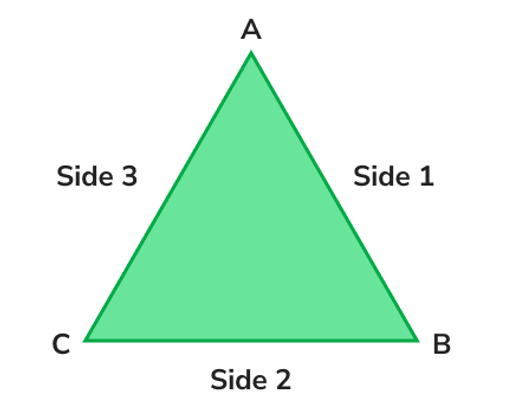 Three Sides: These are the straight line segments connecting each pair of vertices. They form the boundary of the triangle.
Three Sides: These are the straight line segments connecting each pair of vertices. They form the boundary of the triangle.

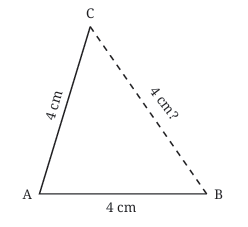
 Draw the Base: Use your ruler to draw a line segment AB that is 4 cm long.
Draw the Base: Use your ruler to draw a line segment AB that is 4 cm long.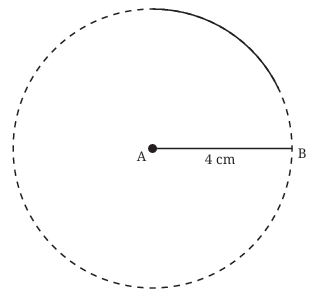 Draw the First Arc: Place the compass point on vertex A. Adjust the compass width to 4 cm (the desired side length). Draw a long arc above the base line. The third vertex, C, must lie somewhere on this arc because every point on this arc is exactly 4 cm away from A
Draw the First Arc: Place the compass point on vertex A. Adjust the compass width to 4 cm (the desired side length). Draw a long arc above the base line. The third vertex, C, must lie somewhere on this arc because every point on this arc is exactly 4 cm away from A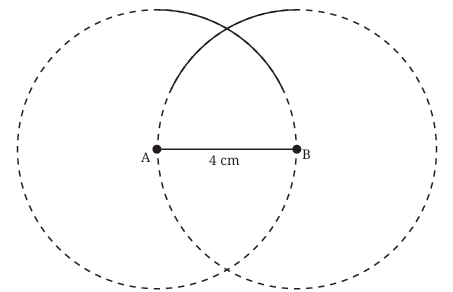 Draw the Second Arc: Now, without changing the compass width (keep it at 4 cm), place the compass point on vertex B. Draw another arc that intersects the first arc. Let the point where the arcs intersect be C.
Draw the Second Arc: Now, without changing the compass width (keep it at 4 cm), place the compass point on vertex B. Draw another arc that intersects the first arc. Let the point where the arcs intersect be C.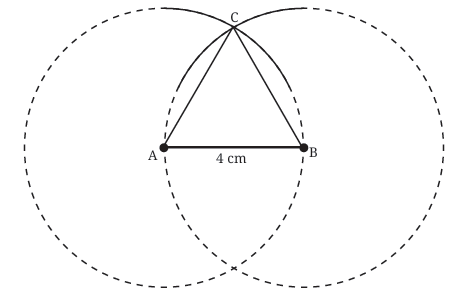 Join the Vertices: Use your ruler to draw straight lines connecting A to C and B to C.
Join the Vertices: Use your ruler to draw straight lines connecting A to C and B to C. Label the ends as A and B.
Label the ends as A and B.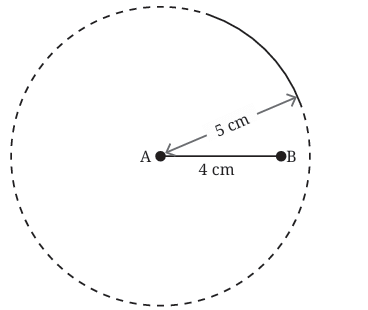 From point A, draw an arc with radius 5 cm. This arc shows all the places where point C (the third corner of the triangle) could be, if it’s 5 cm from A.
From point A, draw an arc with radius 5 cm. This arc shows all the places where point C (the third corner of the triangle) could be, if it’s 5 cm from A.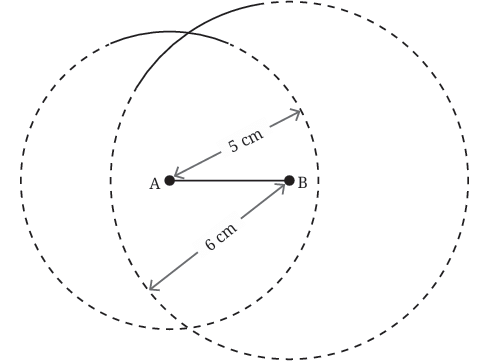 From point B, draw another arc with radius 6 cm. This arc shows where C could be if it’s 6 cm from B.
From point B, draw another arc with radius 6 cm. This arc shows where C could be if it’s 6 cm from B. The place where the two arcs cross is the point C. This point is exactly 5 cm from A and 6 cm from B — just like we need.
The place where the two arcs cross is the point C. This point is exactly 5 cm from A and 6 cm from B — just like we need.
 For example: 3 + 4 = 7 < 8 → Not possible
For example: 3 + 4 = 7 < 8 → Not possible Or walking from the tent to a pole, then from the pole to the tree (longer path).Triangle Inequality Example
Or walking from the tent to a pole, then from the pole to the tree (longer path).Triangle Inequality Example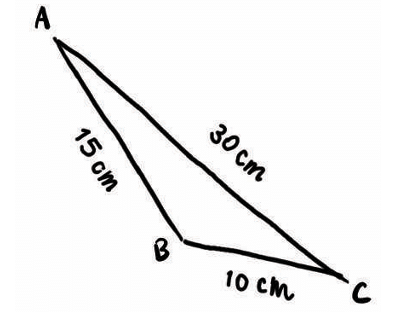 10 + 15 = 25 < 30 → ❌ Not valid
10 + 15 = 25 < 30 → ❌ Not valid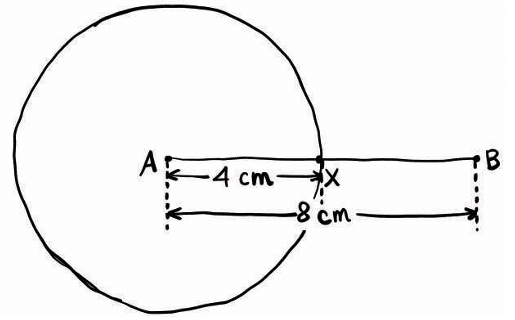 Every point on this circle is 4 cm away from A. This circle shows all the places where point X could be, such that AX = 4 cm.
Every point on this circle is 4 cm away from A. This circle shows all the places where point X could be, such that AX = 4 cm.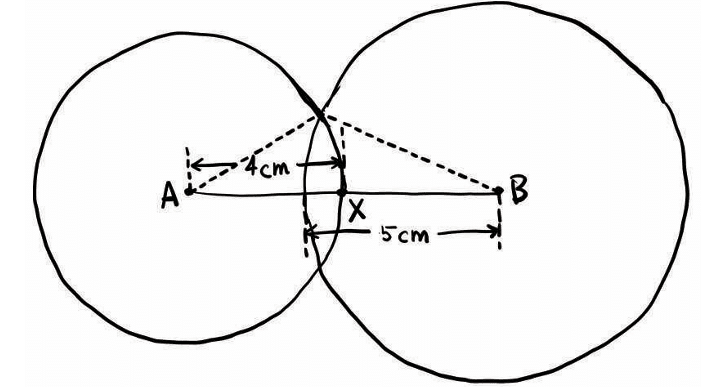
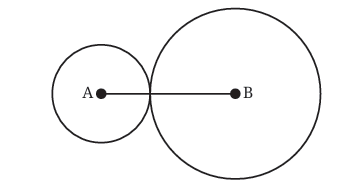
 Case 2: Circles do not intersect
Case 2: Circles do not intersect
 ∠A = 45°
∠A = 45° Join point B to point C – Now you have triangle ABC.
Join point B to point C – Now you have triangle ABC.
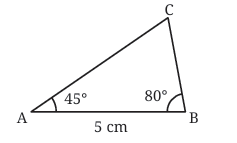 ∠B = 80°
∠B = 80°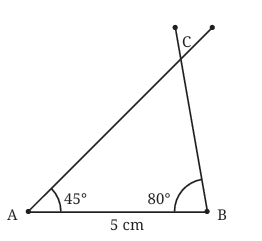 Now, join AC and BC — you have your triangle ABC!
Now, join AC and BC — you have your triangle ABC!
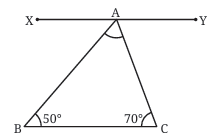 ∠ACB=70°
∠ACB=70°
 Folding the Angles: Next, you fold the triangle along its edges. The key idea is to fold each corner (or vertex) of the triangle so that each angle aligns with one another. When you do this, all three angles of the triangle will meet at a single point.
Folding the Angles: Next, you fold the triangle along its edges. The key idea is to fold each corner (or vertex) of the triangle so that each angle aligns with one another. When you do this, all three angles of the triangle will meet at a single point.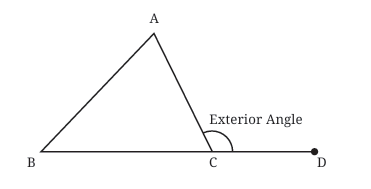
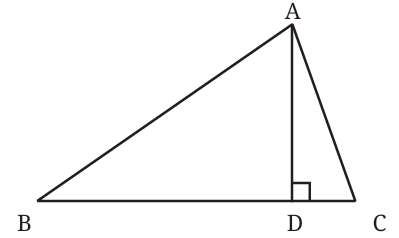 The length of this line, AD, is the altitude of vertex A from the side BC.
The length of this line, AD, is the altitude of vertex A from the side BC.
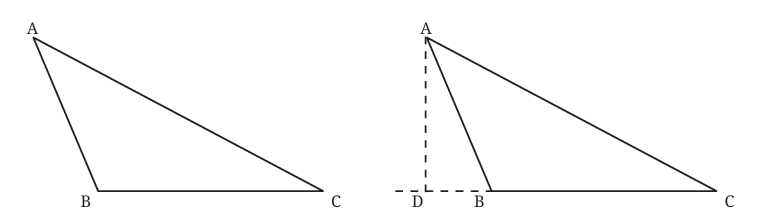 In obtuse triangles (one angle greater than 90°), altitudes might need to be extended outside the triangle, as seen in the figure given below. This is shown by extending the side BC and drawing a perpendicular from A to this extended line.
In obtuse triangles (one angle greater than 90°), altitudes might need to be extended outside the triangle, as seen in the figure given below. This is shown by extending the side BC and drawing a perpendicular from A to this extended line.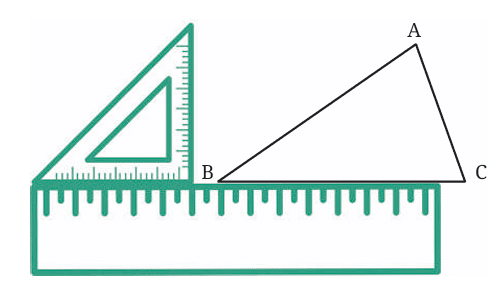
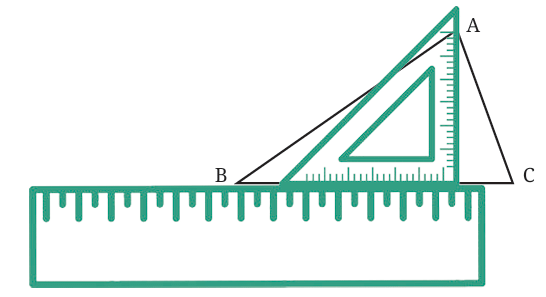 Put the set square on the ruler so that one of its right-angle edges is touching the ruler. This way, we’re guaranteed that one side of the set square forms a perfect 90° angle.
Put the set square on the ruler so that one of its right-angle edges is touching the ruler. This way, we’re guaranteed that one side of the set square forms a perfect 90° angle.
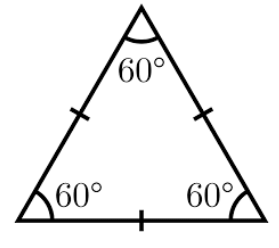
 All three angles are also equal, and each angle measures 60°.
All three angles are also equal, and each angle measures 60°. The two angles opposite these equal sides are also equal.
The two angles opposite these equal sides are also equal. All three angles are different from each other.
All three angles are different from each other.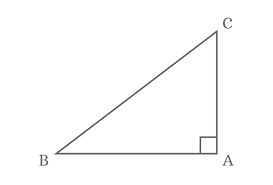 The other two angles are acute (less than 90°).Right-angled Triangle
The other two angles are acute (less than 90°).Right-angled Triangle The other two angles will be acute because the total sum of angles in any triangle must always be 180°.
The other two angles will be acute because the total sum of angles in any triangle must always be 180°.


 Even numbers: Can be grouped in pairs with no leftovers. Example: 2, 4, 6, 8, 10…No pair is left
Even numbers: Can be grouped in pairs with no leftovers. Example: 2, 4, 6, 8, 10…No pair is left Odd numbers: Always leave one unpaired object. Example: 1, 3, 5, 7, 9…One unpaired leftWhat happens when you add two odd numbers?
Odd numbers: Always leave one unpaired object. Example: 1, 3, 5, 7, 9…One unpaired leftWhat happens when you add two odd numbers?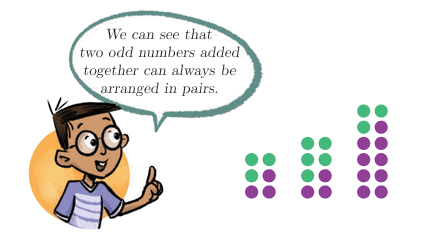 The sum of two odd numbers can always be arranged in pairs, meaning the sum is even.
The sum of two odd numbers can always be arranged in pairs, meaning the sum is even. A 3 × 4 grid has 12 squares (even).
A 3 × 4 grid has 12 squares (even). If n is even, 3n is even, 3n + 4 (even + even) is even.
If n is even, 3n is even, 3n + 4 (even + even) is even.
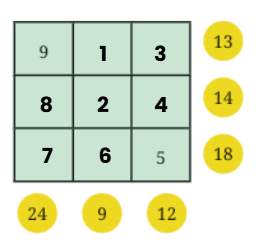
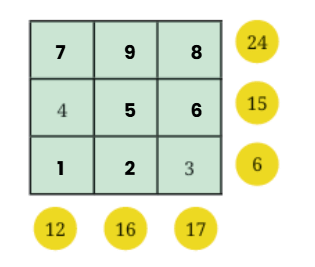


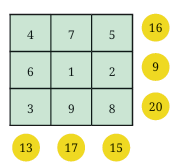

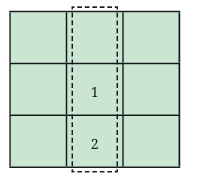
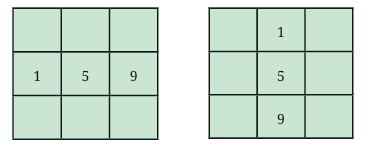
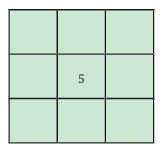 The number 5 must be at the center of the magic square.
The number 5 must be at the center of the magic square.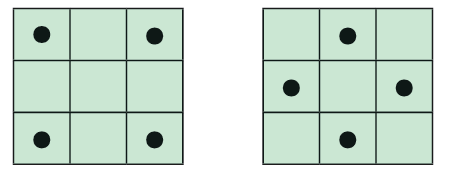

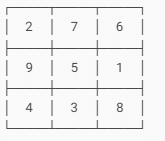

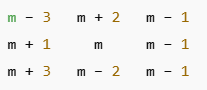
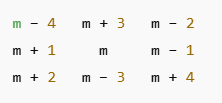



 One such 3 × 3 magic square is found on a pillar in a temple in Palani, Tamil Nadu, dating back to the 8th century CE.
One such 3 × 3 magic square is found on a pillar in a temple in Palani, Tamil Nadu, dating back to the 8th century CE. Magic squares are also found in homes and shops, especially in the Navagraha Yantra, which connects magic squares with planets like:
Magic squares are also found in homes and shops, especially in the Navagraha Yantra, which connects magic squares with planets like: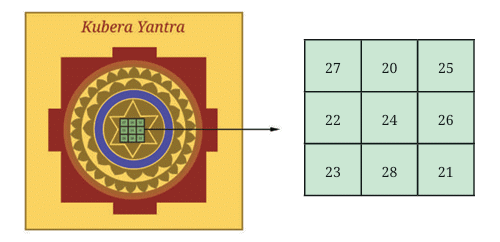






 First Fold: Fold the sheet horizontally exactly in half. You’ve created a new line (crease) in the middle.
First Fold: Fold the sheet horizontally exactly in half. You’ve created a new line (crease) in the middle.
 More Folds: Make another horizontal fold in the already folded sheet.
More Folds: Make another horizontal fold in the already folded sheet.  Vertical Fold: Now, unfold the paper back to the original square. Make a vertical fold down the middle. How does this new vertical line relate to the horizontal lines you made earlier?
Vertical Fold: Now, unfold the paper back to the original square. Make a vertical fold down the middle. How does this new vertical line relate to the horizontal lines you made earlier? 
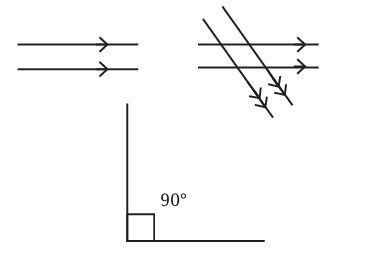 Perpendicular Lines: We draw a small square symbol at the point of intersection where the right angle (90°) is formed.Representation of Parallel and Perpendicular Lines
Perpendicular Lines: We draw a small square symbol at the point of intersection where the right angle (90°) is formed.Representation of Parallel and Perpendicular Lines
 Call this new crease m.
Call this new crease m.






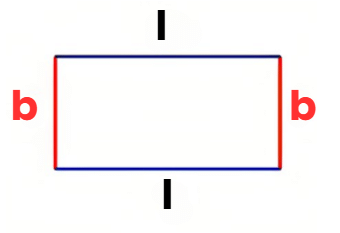 Perimeter formula: Add all sides of the rectangle
Perimeter formula: Add all sides of the rectangle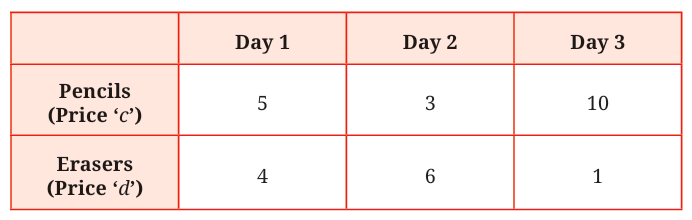 A table gives the number of pencils and erasers sold over 3 days:
A table gives the number of pencils and erasers sold over 3 days:

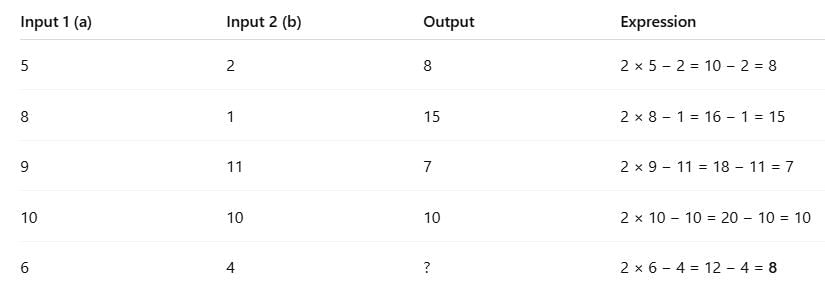

 Look at the remainder
Look at the remainder
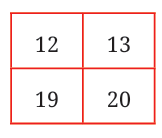

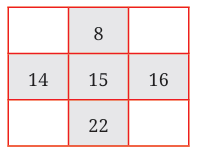



 Yes, one screw was bit longer than the other
Yes, one screw was bit longer than the other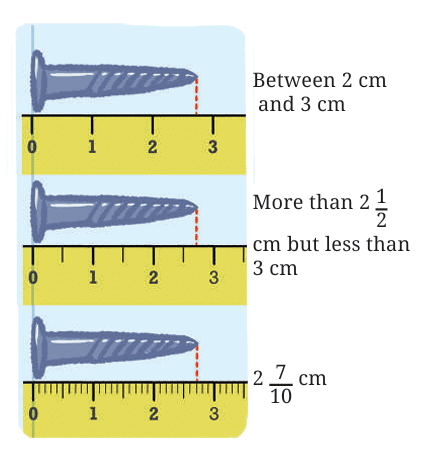
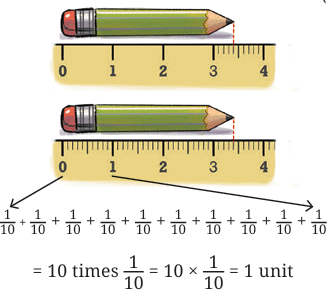
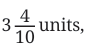
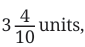
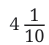 is read as “four and one-tenth”
is read as “four and one-tenth”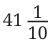 is read as “forty-one and one-tenth”
is read as “forty-one and one-tenth”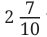
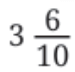
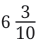
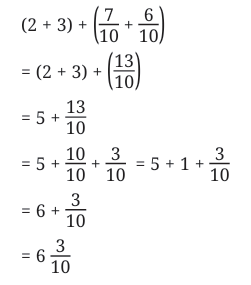
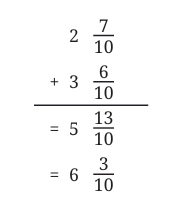
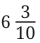
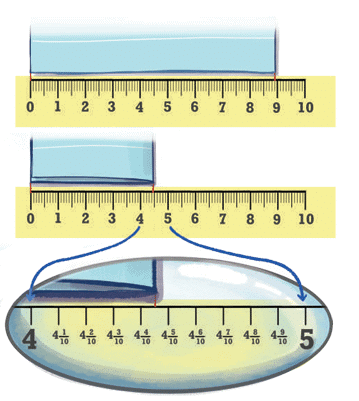
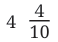
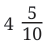

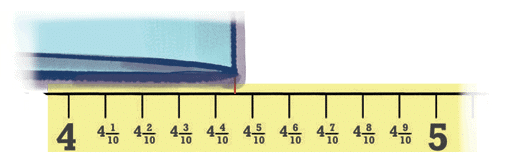

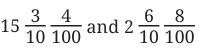
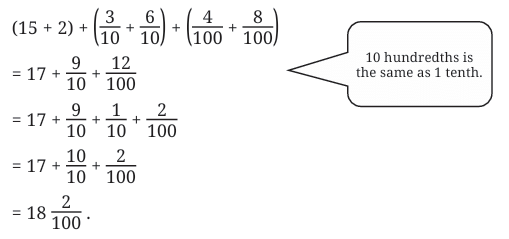
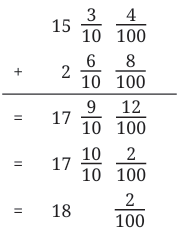
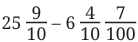
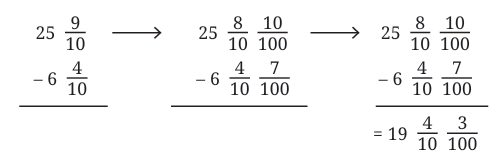
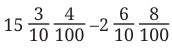
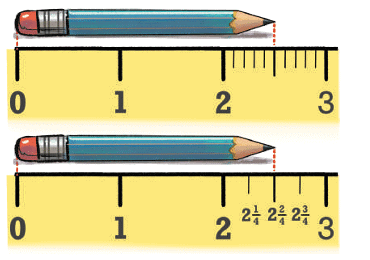 The other is marked in quarters (¼, ½, ¾…)
The other is marked in quarters (¼, ½, ¾…)
 Dividing one-tenth (1/10) by 10 gives one-hundredth (1/100).
Dividing one-tenth (1/10) by 10 gives one-hundredth (1/100). …and so on!
…and so on!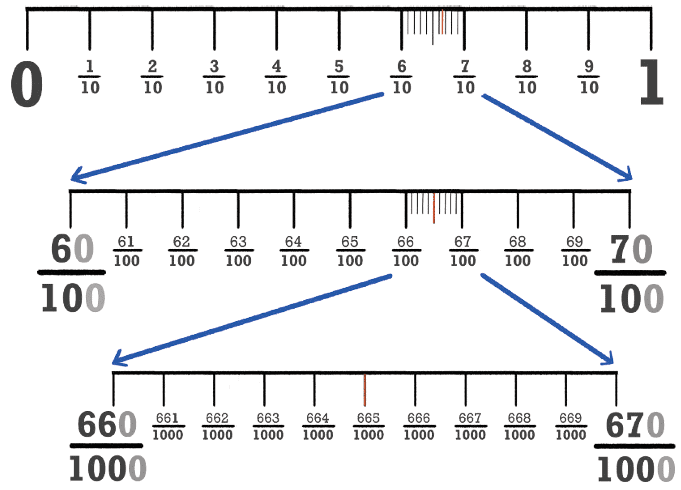

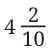
 Fractional Parts (tenths, hundredths, etc.) are to the right of the decimal point.
Fractional Parts (tenths, hundredths, etc.) are to the right of the decimal point.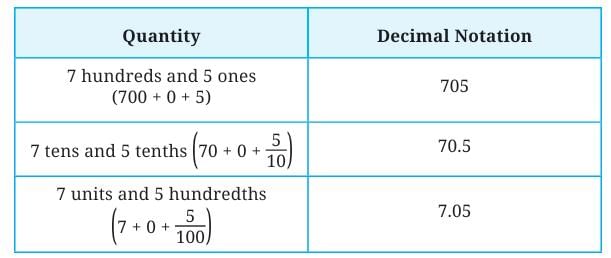


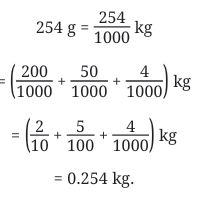

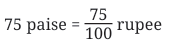
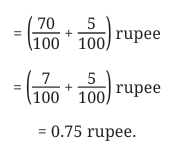
 The 4th division after 1 is 1.4.
The 4th division after 1 is 1.4.

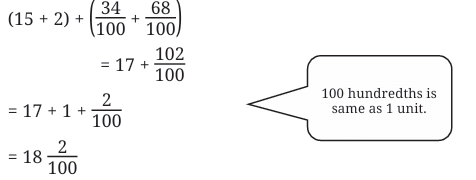
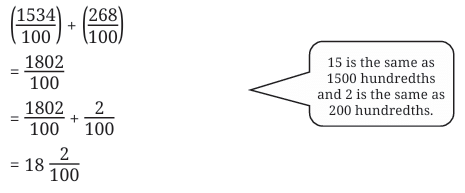
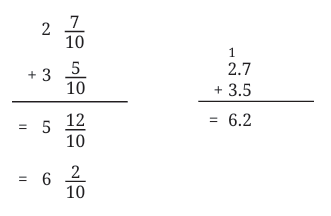 Total = 6 + 2/10 = 6.2 m
Total = 6 + 2/10 = 6.2 m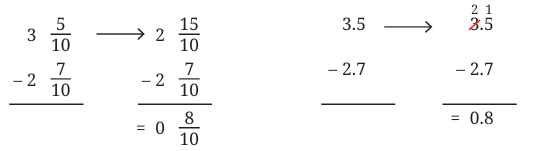 2.7 = 2 + 7/10So, difference = 8/10 = 0.8
2.7 = 2 + 7/10So, difference = 8/10 = 0.8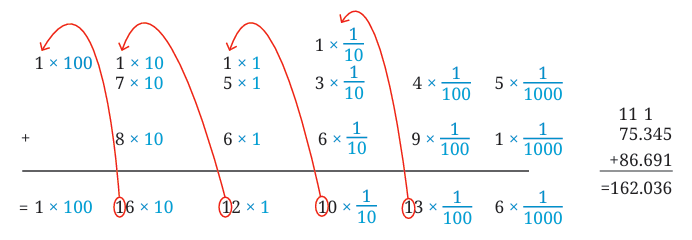
 This could be dangerous when giving medicine.
This could be dangerous when giving medicine. This shows why it’s important to know what decimals mean in real measurements.
This shows why it’s important to know what decimals mean in real measurements. Some countries today use comma instead of a dot (e.g., 1,000.5 becomes 1.000,5).
Some countries today use comma instead of a dot (e.g., 1,000.5 becomes 1.000,5).







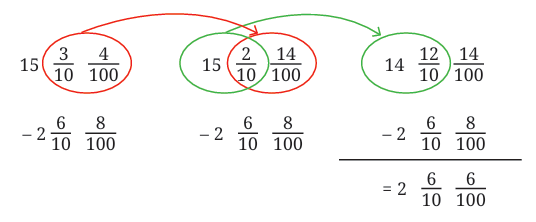
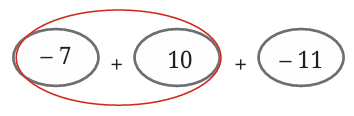 Group the first two terms:
Group the first two terms: Group the last two terms:
Group the last two terms:
 Wear her hat first, then her shoes, or
Wear her hat first, then her shoes, or Wear her shoes first, then her hat.
Wear her shoes first, then her hat.
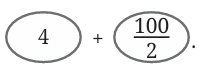
 This Image is correct
This Image is correct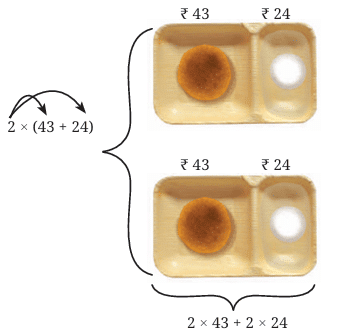
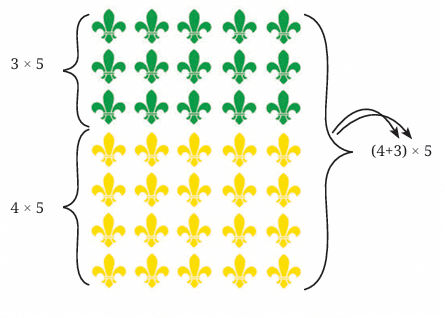
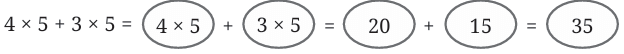



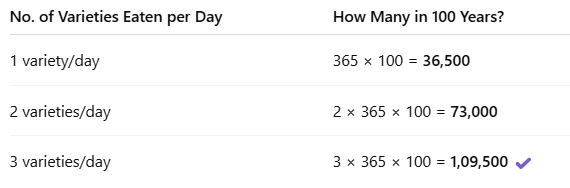

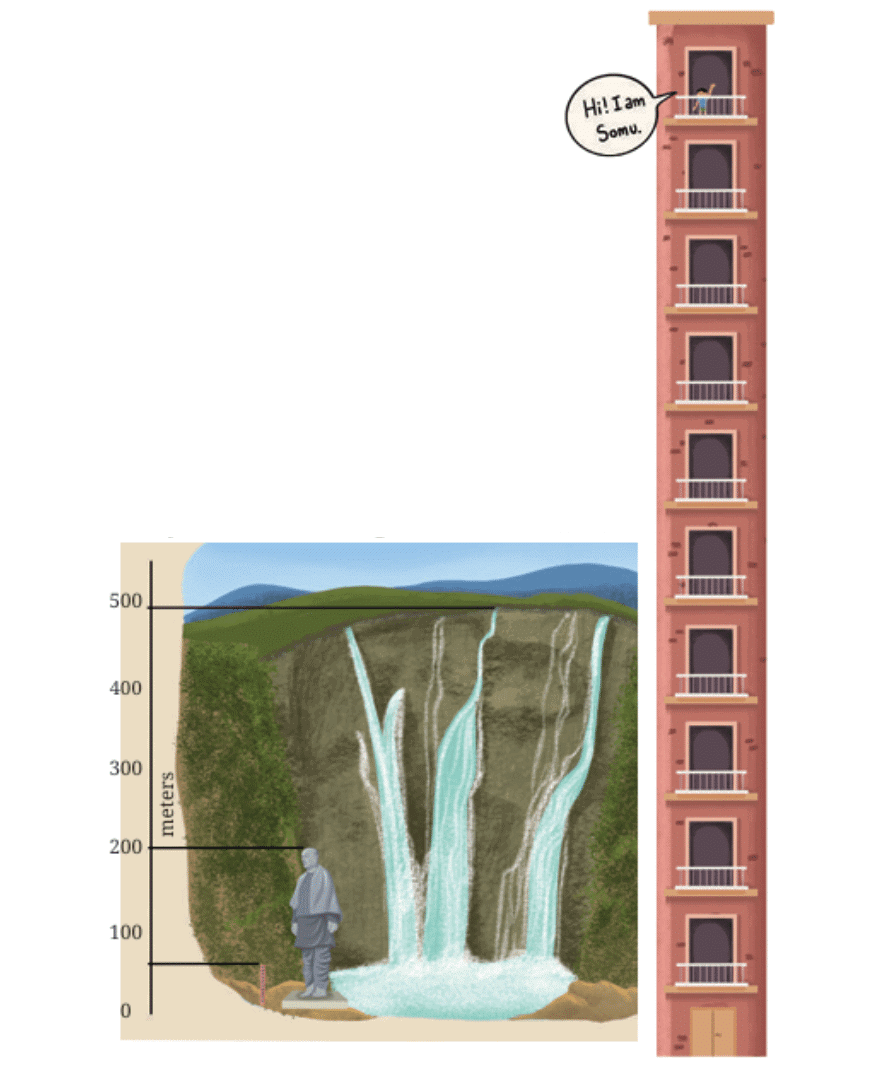 Each floor is about 4 times his height.
Each floor is about 4 times his height. 1 Lakh Varieties of Rice
1 Lakh Varieties of Rice

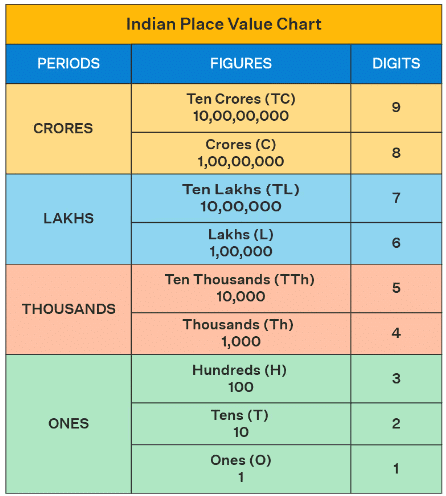













 But saying “about 75,000 people live there” gives a quick idea without needing to know the exact count.
But saying “about 75,000 people live there” gives a quick idea without needing to know the exact count.
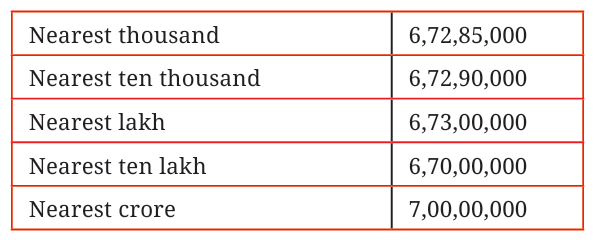

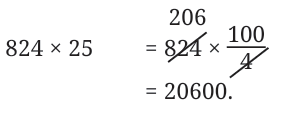 Then, 206 × 100 = 20600
Then, 206 × 100 = 20600