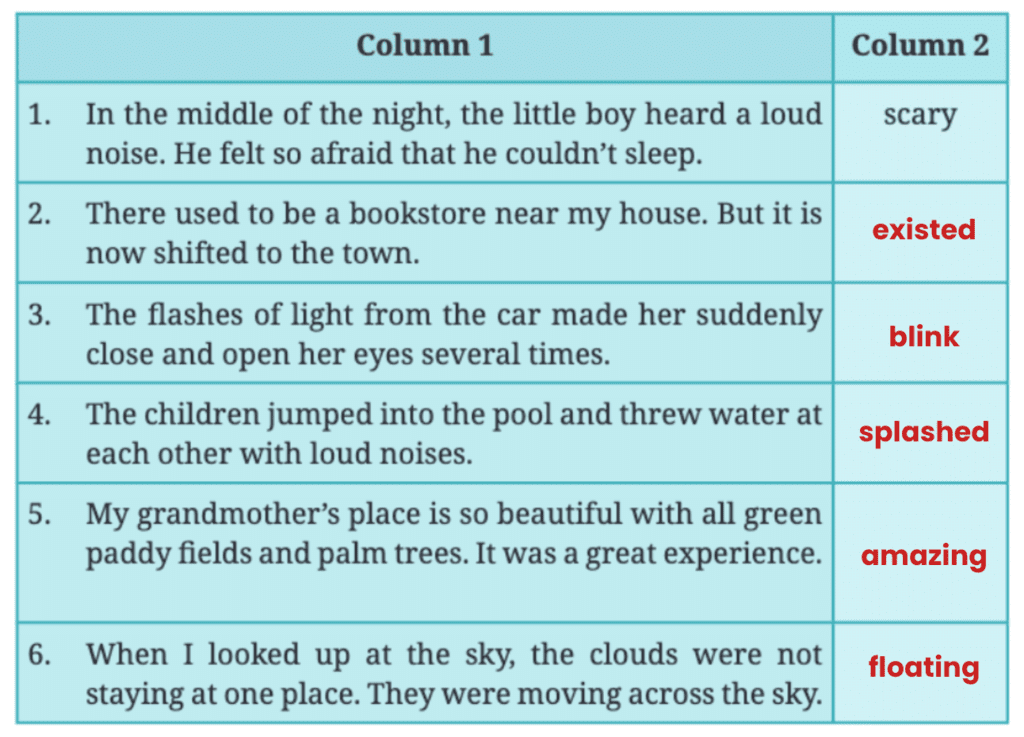
Page No. 24
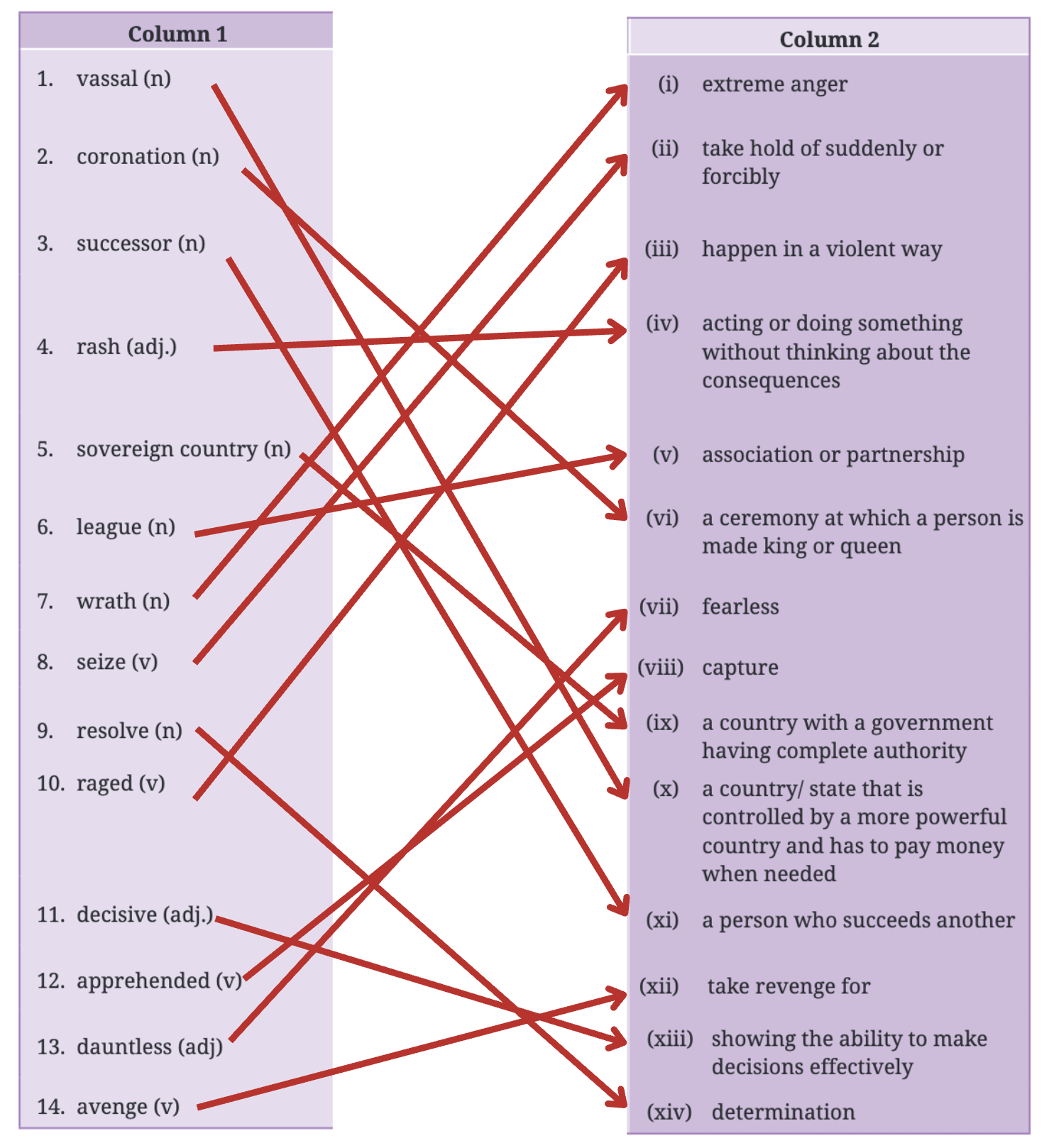
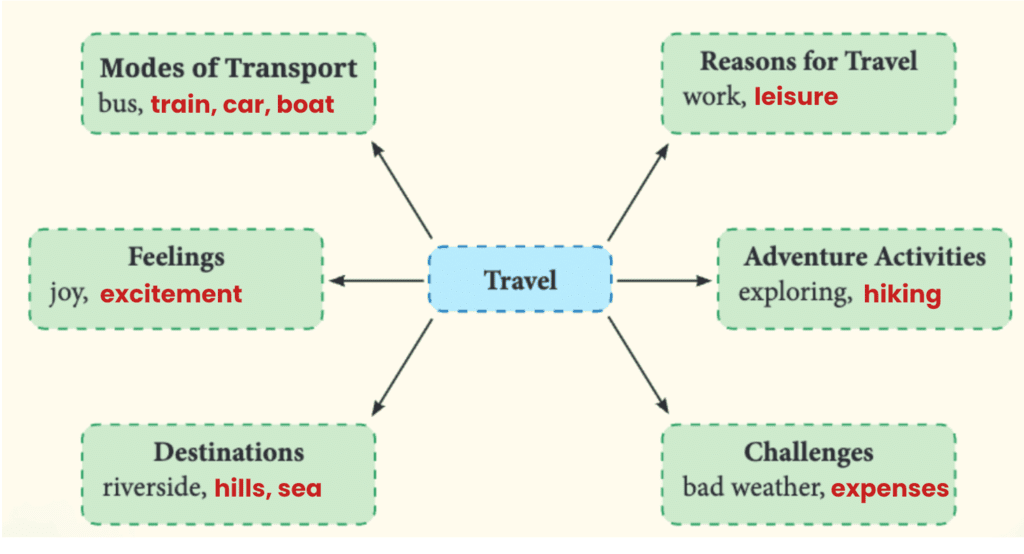
Simple Expressions
Q: Choose your favourite number and write as many expressions as you can having that value.
Ans: Let’s choose the number 12. Expressions with the value 12 are:
- 10 + 2
- 15 – 3
- 3 × 4
- 24 ÷ 2
Page No. 25
Figure it Out
Q1: Fill in the blanks to make the expressions equal on both sides of the = sign:
(a) 13 + 4 = ______ + 6
Ans: 13 + 4 = 17, so 11 + 6 = 17. The blank is 11.
(b) 22 + ______ = 6 × 5
Ans: 6 × 5 = 30, so 22 + 8 = 30. The blank is 8.
(c) 8 × ______ = 64 ÷ 2
Ans: 64 ÷ 2 = 32, so 8 × 4 = 32. The blank is 4.
(d) 34 – ______ = 25
Ans: 34 – 9 = 25. The blank is 9.
Q2: Arrange the following expressions in ascending (increasing) order of their values.
(a) 67 – 19
(b) 67 – 20
(c) 35 + 25
(d) 5 × 11
(e) 120 ÷ 3
Ans: Calculate each expression:
- 67 – 19 = 48
- 67 – 20 = 47
- 35 + 25 = 60
- 5 × 11 = 55
- 120 ÷ 3 = 40
Ascending order: 40 < 47 < 48 < 55 < 60
So, the order is: 120 ÷ 3 < 67 – 20 < 67 – 19 < 5 × 11 < 35 + 25.
Q3: Which is greater? 1023 + 125 or 1022 + 128?
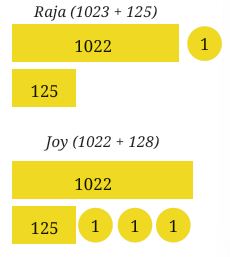
Imagining a situation could help us answer this without finding the values. Raja had 1023 marbles and got 125 more today. Now he has 1023 + 125 marbles. Joy had 1022 marbles and got 128 more today. Now he has 1022 + 128 marbles. Who has more?
Ans: Raja had 1023 marbles and got 125 more (1023 + 125). Joy had 1022 marbles and got 128 more (1022 + 128).
Raja started with 1 more marble than Joy, but Joy got 3 more marbles than Raja today.
So, Joy has 2 more marbles. Therefore, 1023 + 125 < 1022 + 128.
Q4: Which is greater? 113 – 25 or 112 – 24?
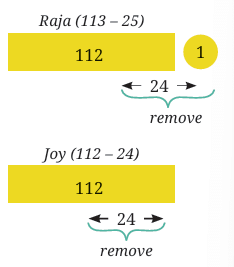
Imagine a situation, Raja had 113 marbles and lost 25 of them. He has 113 – 25 marbles. Joy had 112 marbles and lost 24 today. He has 112 – 24 marbles. Who has more marbles left with them? Raja had 1 marble more than Joy. But he also lost 1 marble more than Joy did. Therefore, they have an equal number of marbles now. That is,
Ans: Raja had 113 marbles and lost 25 (113 – 25). Joy had 112 marbles and lost 24 (112 – 24).
Raja started with 1 more marble but lost 1 more than Joy.
So, they have the same number of marbles now. Therefore, 113 – 25 = 112 – 24.
Page No. 26
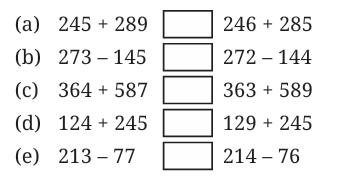
Q1: Use ‘>’ or ‘<’ or ‘=’ in each of the following expressions to compare them. Can you do it without complicated calculations? Explain your thinking in each case.
Ans:
(a) 245 + 289 > 246 + 285
(b) 273 − 144 = 272 − 144
(c) 364 + 587 < 363 + 589
(d) 124 + 245 < 129 + 245
(e) 213 − 77 < 214 − 76
Page No. 28
Terms in Expressions

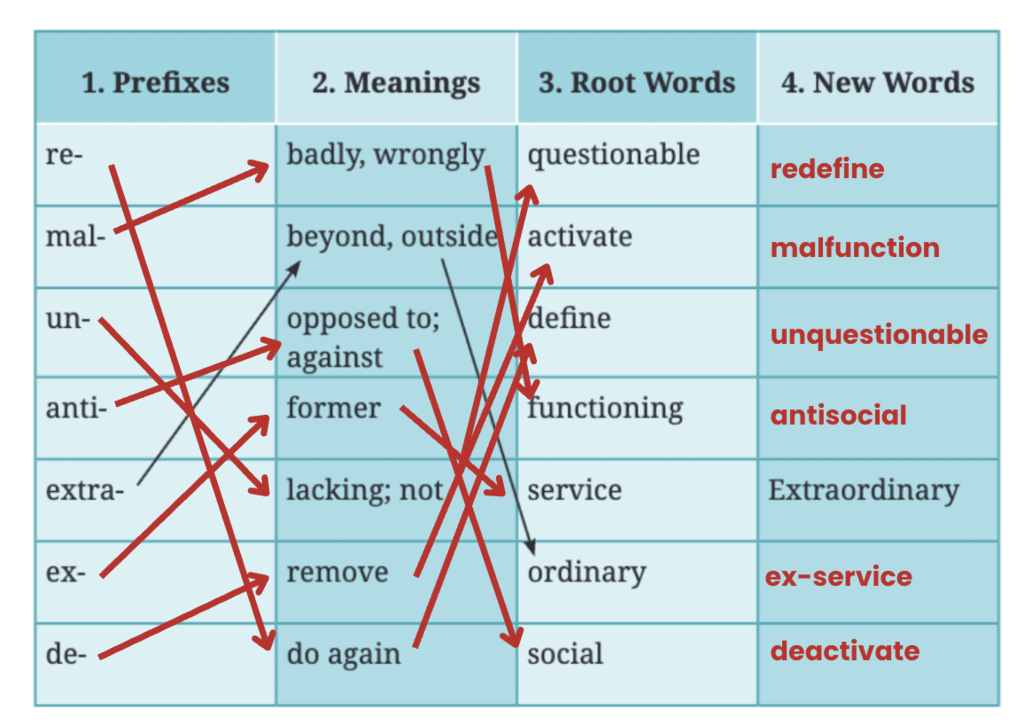
Suppose we have the expression 30 + 5 × 4 without any brackets. Does it have no meaning? When there are expressions having multiple operations, and the order of operations is not specified by the brackets, we use the notion of terms to determine the order. Terms are the parts of an expression separated by a ‘+’ sign. For example, in 12+7, the terms are 12 and 7, as marked below.

We will keep marking each term of an expression as above. Note that this way of marking the terms is not a usual practice. This will be done until you become familiar with this concept. Now, what are the terms in 83 – 14? We know that subtracting a number is the same as adding the inverse of the number. Recall that the inverse of a given number has the sign opposite to it. For example, the inverse of 14 is –14, and the inverse of –14 is 14. Thus, subtracting 14 from 83 is the same as adding –14 to 83. That is,
Thus, the terms of the expression 83 – 14 are 83 and –14.
Q1: Check if replacing subtraction by addition in this way does not change the value of the expression, by taking different examples.
Ans: Subtraction can be written as adding the inverse. For example:
- 83 – 14 = 83 + (-14). Calculate: 83 – 14 = 69, and 83 + (-14) = 69.
- 20 – 5 = 20 + (-5). Calculate: 20 – 5 = 15, and 20 + (-5) = 15.
In both cases, the value remains the same.
Q2: Can you explain why subtracting a number is the same as adding its inverse, using the Token Model of integers that we saw in the Class 6 textbook of mathematics?
Ans: In the Token Model of integers:
- A positive token represents +1
- A negative token represents -1
When we subtract a number, it means we are removing that many positive tokens.
But removing positive tokens is the same as adding negative tokens of the same value.
Example:
Let’s take the expression: 5 – 3
- Start with 5 positive tokens: +1 +1 +1 +1 +1
- Subtract 3 means removing 3 positive tokens:
Remove +1 +1 +1 - We are left with: +1 +1 → which is 2
Now, look at the expression: 5 + (-3)
- Start with 5 positive tokens: +1 +1 +1 +1 +1
- Add 3 negative tokens: -1 -1 -1
- Combine them: (+1 and -1 cancel each other)
So 3 positive and 3 negative tokens cancel out - Left with: +1 +1 → which is 2
Conclusion:
Subtracting a number is the same as adding its inverse (opposite).
That’s why:
5 – 3 = 5 + (-3) → both give the same result.
Page No. 29 & 30
Swapping and GroupingQ1: In the following table, some expressions are given. Complete the table.

Ans:
Q2: Does changing the order in which the terms are added give different values?
Ans: No, changing the order of addition does not change the value. For example, 6 + (-4) = 2, and (-4) + 6 = 2.
This is due to the commutative property of addition.
Q3: Will this also hold when there are terms having negative numbers as well? Take some more expressions and check.
Ans: Yes, it holds. For example:
- (-5) + 7 = 2, and 7 + (-5) = 2.
- (-3) + (-2) = -5, and (-2) + (-3) = -5.
Swapping terms does not change the value.
Q4: Can you explain why this is happening using the Token Model of integers that we saw in the Class 6 textbook of mathematics?
Ans: In the Token Model of integers:
- A positive token means +1
- A negative token means –1
- When a positive token and a negative token are put together, they cancel each other (because +1 and -1 = 0)
Let’s understand this with an example:
Suppose you start with 0 tokens.
Now if you add 5 negative tokens (–5) and 5 positive tokens (+5):
- You now have:
+1 +1 +1 +1 +1
-1 -1 -1 -1 -1 - Pair each positive token with a negative token:
(+1, -1), (+1, -1), (+1, -1), (+1, -1), (+1, -1) - Each pair cancels out to 0.
So, in the end, you are left with 0 again.
Why this is important:
This shows how positive and negative numbers balance each other.
Whenever you add or subtract, the total depends on how many positive or negative tokens you finally have.
For example:
- 3 – 5
= 3 positive tokens and 5 negative tokens
= (+1 +1 +1) and (–1 –1 –1 –1 –1)
Cancel 3 pairs → Left with (–1 –1)
So, 3 – 5 = -2
This is why subtraction with integers can give negative answers, and the Token Model helps us see this clearly.
Page No. 31 & 32
Q5: Does adding the terms of an expression in any order give the same value? Take some more expressions and check. Consider expressions with more than 3 terms also.
Ans: Yes, adding the terms of an expression in any order gives the same value. This is because addition is commutative and associative, which means:
- Commutative: Changing the order of numbers doesn’t change the sum.
(Example: 4 + 5 = 5 + 4 = 9) - Associative: Grouping numbers differently doesn’t change the sum.
(Example: (2 + 3) + 4 = 2 + (3 + 4) = 9)
Let’s check with more terms:
Example 1:
7 + (-2) + 5 + (-3)
Try adding in different orders:
- (7 + 5) + (-2) + (-3) = 12 – 2 – 3 = 7
- 7 + (-2) + (-3) + 5 = 7 – 2 – 3 + 5 = 7
- (-2 + 5) + (-3 + 7) = 3 + 4 = 7
All give the same result.
Q6: Can you explain why this is happening using the Token Model of integers that we saw in the Class 6 textbook of mathematics?
Ans: In the Token Model:
- Positive numbers are shown as positive tokens (+1 each)
- Negative numbers are shown as negative tokens (–1 each)
- A positive token and a negative token together cancel out (because +1 + (–1) = 0)
When adding integers:
- You’re simply collecting tokens from all terms
- You can collect them in any order — the total number of positive and negative tokens stays the same
- So the final result remains the same, no matter how you arrange the terms.
Therefore, the addition of terms in any order gives the same value.
Q7: Manasa is adding a long list of numbers. It took her five minutes to add them all and she got the answer 11749. Then she realised that she had forgotten to include the fourth number 9055. Does she have to start all over again?
Ans: No, she doesn’t need to start over.
She can add 9055 to 11749: 11749 + 9055 = 20804.
This is because addition is commutative and associative.
Page no. 32
Example 7: Amu, Charan, Madhu, and John went to a hotel and ordered four dosas. Each dosa cost ₹23, and they wish to thank the waiter by tipping ₹5. Write an expression describing the total cost.
Ans: Cost of 4 dosas = 4 × 23
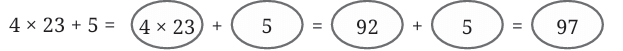
Can the total amount with tip be written as 4 × 23 + 5? Evaluating it, we get
Thus, 4 × 23 + 5 is a correct way of writing the expression.
Q: If the total number of friends goes up to 7 and the tip remains the same, how much will they have to pay? Write an expression for this situation and identify its terms.
Ans: Cost of 7 dosas = 7 × 23. Total cost with tip = 7 × 23 + 5.
Terms: 7 × 23, 5.
Evaluate: 7 × 23 = 161, 161 + 5 = 166. They pay ₹166.
The terms in the expression 7 × 23 + 5 are 7 × 23, 5.
Example 8: Children in a class are playing “Fire in the mountain, run, run, run!”. Whenever the teacher calls out a number, students are supposed to arrange themselves in groups of that number. Whoever is not part of the announced group size, is out. Ruby wanted to rest and sat on one side. The other 33 students were playing the game in the class. The teacher called out ‘5’. Once children settled,
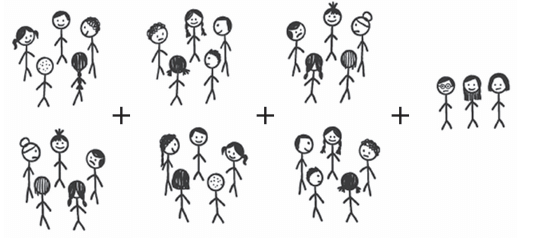
Ruby wrote 6 × 5 + 3 (understood as 3 more than 6 × 5)
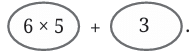
Q: Think and discuss why she wrote this. The expression written as a sum of terms is—
Ans: Ruby observed what happened in the game:
- The children had to form groups of 5.
- She noticed that there were 6 full groups of 5 students each.
- That makes 6 × 5 = 30 students.
- But the total number of children playing was 33.
- So, 3 children were left out who could not fit into a full group of 5.
Therefore, Ruby wrote:
6 × 5 + 3,
which means:
- 30 students are in complete groups (6 groups of 5),
- and 3 students are left out.
Final Expression:
6 × 5 + 3 — written as a sum of terms:
(6 × 5) + 3
Page No. 33
Q1: For each of the cases below, write the expression and identify its terms:
If the teacher had called out ‘4’, Ruby would write ____________
If the teacher had called out ‘7’, Ruby would write ____________
Write expressions like the above for your class size.
Ans:
- For 4: 33 ÷ 4 = 8 groups of 4 with 1 left (33 – 32 = 1).
If the teacher had called out ‘4’, Ruby would write
Expression: 8 × 4 + 1.
Terms: 8 × 4, 1. - For 7: 33 ÷ 7 = 4 groups of 7 with 5 left (33 – 28 = 5).
If the teacher had called out ‘4’, Ruby would write
Expression: 4 × 7 + 5.
Terms: 4 × 7, 5. - For a class of 30: For 5, 30 ÷ 5 = 6 groups.
If the teacher had called out ‘4’, Ruby would write
Expression: 6 × 5.
Terms: 6 × 5.
Q2: Identify the terms in the two expressions for ₹432.
Ans:
- 432 = 4 × 100 + 1 × 20 + 1 × 10 + 2 × 1. Terms: 4 × 100, 1 × 20, 1 × 10, 2 × 1.
- 432 = 8 × 50 + 1 × 10 + 4 × 5 + 2 × 1. Terms: 8 × 50, 1 × 10, 4 × 5, 2 × 1.
Q3: Can you think of some more ways of giving ₹432 to someone?
Ans: Some more ways to gave ₹432 to someone are as follows:
- 4 × 100 + 3 × 10 + 2 × 1 = 400 + 30 + 2 = 432.
Terms: 4 × 100, 3 × 10, 2 × 1. - 2 × 100 + 4 × 50 + 3 × 10 + 2 × 1 = 200 + 200 + 30 + 2 = 432.
Terms: 2 × 100, 4 × 50, 3 × 10, 2 × 1.
Page No. 34
Q1: What is the expression for the arrangement in the right making use of the number of yellow and blue squares?
Ans: The right arrangement has 2 groups of (5 yellow + 3 blue). Expression: 2 × (5 + 3).
Other forms: 5 + 3 + 5 + 3 or 5 × 2 + 3 × 2.
Figure it Out
Q1: Find the values of the following expressions by writing the terms in each case.
(a) 28 – 7 + 8
Ans: Terms: 28, -7, 8.
Expression: 28 + (-7) + 8 = 21 + 8 = 29.
(b) 39 – 2 × 6 + 11
Ans: Terms: 39, -2 × 6, 11.
Expression: 39 + (-2 × 6) + 11 = 39 – 12 + 11 = 38.
(c) 40 – 10 + 10 + 10
Ans: Terms: 40, -10, 10, 10.
Expression: 40 + (-10) + 10 + 10 = 30 + 10 + 10 = 50.
(d) 48 – 10 × 2 + 16 ÷ 2
Ans: Terms: 48, -10 × 2, 16 ÷ 2.
Expression: 48 + (-10 × 2) + (16 ÷ 2) = 48 – 20 + 8 = 36.
(e) 6 × 3 – 4 × 8 × 5
Ans: Terms: 6 × 3, -4 × 8 × 5.
Expression: 6 × 3 + (-4 × 8 × 5) = 18 – 160 = -142.
Q2: Write a story/situation for each of the following expressions and find their values.
(a) 89 + 21 – 10
Ans: Story: Ria had 89 candies, got 21 more, and gave 10 to her friend. How many candies does she have now?
Value: 89 + 21 – 10 = 100.
(b) 5 × 12 – 6
Ans: Story: A shop sells 5 packs of 12 pencils each but removes 6 defective ones. How many pencils are left?
Value: 5 × 12 – 6 = 60 – 6 = 54.
(c) 4 × 9 + 2 × 6
Ans: Story: A family buys 4 pizzas costing ₹9 each and 2 drinks costing ₹6 each. What is the total cost?
Value: 4 × 9 + 2 × 6 = 36 + 12 = 48.
Q3: For each of the following situations, write the expression describing the situation, identify its terms and find the value of the expression.
(a) Queen Alia gave 100 gold coins to Princess Elsa and 100 gold coins to Princess Anna last year. Princess Elsa used the coins to start a business and doubled her coins. Princess Anna bought jewellery and has only half of the coins left. Write an expression describing how many gold coins Princess Elsa and Princess Anna together have.
Ans: Elsa’s coins: 2 × 100. Anna’s coins: 100 ÷ 2.
Expression: 2 × 100 + 100 ÷ 2.
Terms: 2 × 100, 100 ÷ 2.
Value: 2 × 100 + 100 ÷ 2 = 200 + 50 = 250 coins.
(b) A metro train ticket between two stations is ₹40 for an adult and ₹20 for a child. What is the total cost of tickets:
(i) for four adults and three children?
Ans: Expression: 4 × 40 + 3 × 20. Terms: 4 × 40, 3 × 20.
Value: 4 × 40 + 3 × 20 = 160 + 60 = 220. Total cost is ₹220.
(ii) for two groups having three adults each?
Ans: Expression: 2 × (3 × 40). Terms: 2 × (3 × 40).
Value: 2 × (3 × 40) = 2 × 120 = 240. Total cost is ₹240.
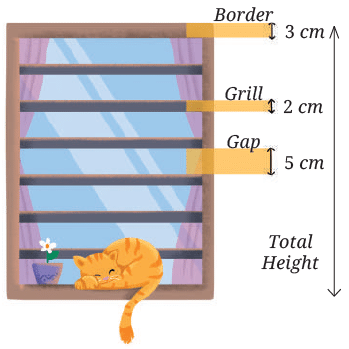
(c) Find the total height of the window by writing an expression describing the relationship among the measurements shown in the picture.
Ans: Total height of the window is as follows:
Expression: 5 X 7 + 2 X 6 + 3 X 2
Terms: 5 X 7, 2 X 6, 3 X 2
Value: 35 + 12 + 6 = 53 cm.
Calculation: 5 X 7 + 2 X 6 + 3 X 2 = 35 + 12 + 6 = 53 cm
Page No. 37, 38 & 39
Tinker the Terms I
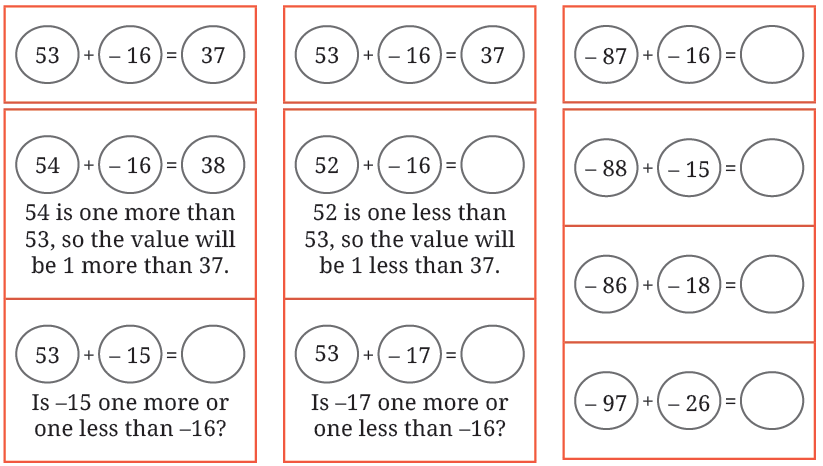
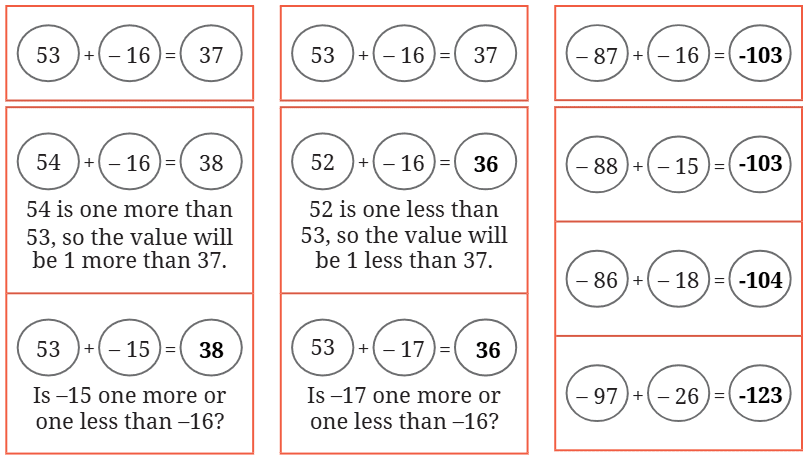
What happens to the value of an expression if we increase or decrease the value of one of its terms? Some expressions are given in following three columns. In each column, one or more terms are changed from the first expression. Go through the example (in the first column) and fill the blanks, doing as little computation as possible.
Ans:
Is −15 one more or one less than −16?
Ans: Yes, –15 is one more than
–16, so the value will be 1
more than 37.
Is −17 one more or one less than −16?
Ans: Yes, –17 is one less than
–16, so the value will be 1
less than 37.
Figure it Out

Q1: Fill in the blanks with numbers, and boxes with operation signs such that the expressions on both sides are equal.
(a) 24 + (6 – 4) = 24 + 6____
Ans: 24 + (6 – 4) = 24 + 6 – 4 = 26

(b) 38 + (_____ _____) = 38 + 9 – 4
Ans: 38 + (9 – 4) = 38 + 9 – 4 = 43

(c) 24 – (6 +4) = 246 – 4
Ans: 24 – (6 + 4) = 24 – 6 – 4 = 14

(d) 24 – 6 – 4 = 24 – 6_____
Ans: 24 – 6 – 4 = 24 – 6 – 4 = 14


(e) 27 – (8 + 3) = 278 3
Ans: 27 – (8 + 3) = 27 – 8 – 3 = 16

(f ) 27– (__________) = 27 – 8 + 3
Ans: 27 – (8 – 3) = 27 – 8 + 3 = 22
Q2: Remove the brackets and write the expression having the same value.
(a) 14 + (12 + 10)
Ans: 14 + (12 + 10) = 14 + 12 + 10.
(b) 14 – (12 + 10)
Ans: 14 – (12 + 10) = 14 – 12 – 10.
(c) 14 + (12 – 10)
Ans: 14 + (12 – 10) = 14 + 12 – 10.
(d) 14 – (12 – 10)
Ans: 14 – (12 – 10) = 14 – 12 + 10.
(e) -14 + 12 – 10
Ans: No brackets to remove. Expression: -14 + 12 – 10.
(f) 14 – (-12 – 10)
Ans: 14 – (-12 – 10) = 14 + 12 + 10.
Q3: Find the values of the following expressions. For each pair, first try to guess whether they have the same value. When are the two expressions equal?
(a) (6 + 10) – 2 and 6 + (10 – 2)
Ans: Initial Guess: Different, due to bracket placement.
Values: (6 + 10) – 2 = 16 – 2 = 14,
6 + (10 – 2) = 6 + 8 = 14.
Conclusion: They are equal because (a + b) – c = a + (b – c).
(b) 16 – (8 – 3) and (16 – 8) – 3
Ans: Initial Guess: Different.
Values: 16 – (8 – 3) = 16 – 5 = 11,
(16 – 8) – 3 = 8 – 3 = 5.
Conclusion: They are not equal.
(c) 27 – (18 + 4) and 27 + (-18 – 4)
Ans: Initial Guess: Same, as – (a + b) = -a – b.
Values: 27 – (18 + 4) = 27 – 22 = 5,
27 + (-18 – 4) = 27 – 18 – 4 = 5.
Conclusion: They are equal.
Q4: In each of the sets of expressions below, identify those that have the same value. Do not evaluate them, but rather use your understanding of terms.
(a) 319 + 537, 319 – 537, – 537 + 319, 537 – 319
Ans: Identifications as follows:
- 319 – 537 and –537 + 319 are the same, because changing the order in addition of a negative number results in subtraction.
- 319 + 537 and 537 – 319 are not the same, but they are both positive.
- 319 – 537 and –537 + 319 are negative and equal to each other.
The expressions that have the same value are:
- 319 – 537
- –537 + 319
(b) 87 + 46 – 109, 87 + 46 – 109, 87 + 46 – 109, 87 – 46 + 109, 87 – (46 + 109), (87 – 46) + 109
Ans: The first three are identical: 87 + 46 – 109.
87 – 46 + 109 = (87 – 46) + 109 (associative).
87 – (46 + 109) = 87 – 46 – 109 (different).
Equal: 87 + 46 – 109 (three times)
Also, 87 – 46 + 109 and (87 – 46) + 109 have the same value.
Q5: Add brackets at appropriate places in the expressions such that they lead to the values indicated.
(a) 34 – 9 + 12 = 13
Ans: To get 13, we need to first subtract 9 from 34, then add 12.
So, (34 – 9) + 12 = 25 + 12 = 37 (not correct).
Instead, try 34 – (9 + 12):
34 – (9 + 12) = 34 – 21 = 13.
So, the expression is 34 – (9 + 12) = 13.
(b) 56 – 14 – 8 = 34
Ans: To get 34, we need to subtract 14 and 8 from 56 in the correct order.
(56 – 14) – 8 = 42 – 8 = 34.
So, the expression is (56 – 14) – 8 = 34.
(c) –22 – 12 + 10 + 22 = – 22
Ans: To get –22, we need to group the terms carefully.
–22 – (12 + 10) + 22 = –22 – 22 + 22 = –22.
So, the expression is –22 – (12 + 10) + 22 = –22.
Q6: Using only reasoning of how terms change their values, fill the blanks to make the expressions on either side of the equality (=) equal.
(a) 423 + ______= 419 + ______
Ans: We need to make both sides equal.
423 + ___ = 419 + ___.
423 is 4 more than 419 (423 – 419 = 4).
So, the number on the right side should be 4 more than the number on the left side.
If we put 0 on the left, then 0 + 4 = 4 on the right.
423 + 0 = 419 + 4.
So, the blanks are 0 and 4.
(b) 207 – 68 = 210 – ______
Ans: We need to make both sides equal.
207 – 68 = 210 – ___.
First, calculate 207 – 68 = 139.
So, 210 – ___ = 139.
210 – 139 = 71.
So, the blank is 71.
Q7: Using the numbers 2, 3 and 5, and the operators ‘+’ and ‘–’, and brackets, as necessary, generate expressions to give as many different values as possible. For example, 2 – 3 + 5 = 4 and 3 – (5 – 2) = 0.
Ans: Let’s use 2, 3, and 5 with + and – to get different values:
- 2 + 3 + 5 = 10
- 2 + 3 – 5 = 0
- 2 – 3 + 5 = 4
- 2 – (3 + 5) = –6
- (2 + 3) – 5 = 0
- 3 – (5 – 2) = 0
- 5 – (2 + 3) = 0
- 5 + 3 – 2 = 6
So, the different values are –6, 0, 4, 6, 10.
Q8: Whenever Jasoda has to subtract 9 from a number, she subtracts 10 and adds 1 to it. For example, 36 – 9 = 26 + 1.
(a) Do you think she always gets the correct answer? Why?
Ans: Yes, Jasoda always gets the correct answer.
Subtracting 10 and adding 1 is the same as subtracting 9 because 10 – 1 = 9.
For example, 36 – 9 = 27.
Jasoda does 36 – 10 + 1 = 26 + 1 = 27, which is correct.
(b) Can you think of other similar strategies? Give some examples.
Ans: Yes, we can use other strategies:
Instead of subtracting 9, subtract 8 and subtract 1 more: 36 – 9 = 36 – 8 – 1 = 28 – 1 = 27.
Or, subtract 5 and subtract 4 more: 36 – 9 = 36 – 5 – 4 = 31 – 4 = 27.
Both give the correct answer.
Q9: Consider the two expressions: a) 73 – 14 + 1, b) 73 – 14 – 1. For each of these expressions, identify the expressions from the following collection that are equal to it.
(a) 73 – (14 + 1)
Ans: 73 – (14 + 1) = 73 – 15 = 58.
Expression a) 73 – 14 + 1 = 59 + 1 = 60 (not equal).
Expression b) 73 – 14 – 1 = 59 – 1 = 58 (equal).
So, it matches expression b).
(b) 73 – (14 – 1)
Ans: 73 – (14 – 1) = 73 – 13 = 60.
Expression a) 73 – 14 + 1 = 60 (equal).
Expression b) 73 – 14 – 1 = 58 (not equal).
So, it matches expression a).
(c) 73 + (–14 + 1)
Ans: 73 + (–14 + 1) = 73 + (–13) = 73 – 13 = 60.
Expression a) 73 – 14 + 1 = 60 (equal).
Expression b) 73 – 14 – 1 = 58 (not equal).
So, it matches expression a).
(d) 73 + (–14 – 1)
Ans: 73 + (–14 – 1) = 73 + (–15) = 73 – 15 = 58.
Expression a) 73 – 14 + 1 = 60 (not equal).
Expression b) 73 – 14 – 1 = 58 (equal).
So, it matches expression b).
Removing Brackets—II
Example 15: Lhamo and Norbu went to a hotel. Each of them ordered a vegetable cutlet and a rasgulla. A vegetable cutlet costs ₹43 and a rasgulla costs ₹24. Write an expression for the amount they will have to pay.
Ans: As each of them had one vegetable cutlet and one rasagulla, each of their shares can be represented by 43 + 24.
Q: What about the total amount they have to pay? Can it be described by the expression: 2 × 43 + 24?
Ans: Each person had 1 vegetable cutlet and 1 rasgulla.
Cost of one vegetable cutlet = ₹43
Cost of one rasgulla = ₹24
So, cost for one person = 43 + 24 = ₹67
There are 2 people, so total cost = 2 × (43 + 24) = 2 × 67 = ₹134
The expression 2 × 43 + 24 is not correct because it only adds the cost of two cutlets and only one rasgulla.
But there are two rasgullas, so we must multiply the total cost of one person’s food by 2.
Correct expression is: 2 × (43 + 24)
Q: If another friend, Sangmu, joins them and orders the same items, what will be the expression for the total amount to be paid?
Ans: Cost of one vegetable cutlet = ₹43
Cost of one rasgulla = ₹24
Total cost for one person = 43 + 24 = ₹67
Now, there are 3 people (Lhamo, Norbu, and Sangmu).
So, the total amount to be paid = 3 × (43 + 24)
= 3 × 67 = ₹201
Expression: 3 × (43 + 24)
Page No. 41 & 42
Tinker the Terms II
Example 17: Given 53 × 18 = 954. Find out 63 × 18.
Ans: As 63 × 18 means 63 times 18,
63 × 18 = (53 + 10) × 18
= 53 ×18 + 10×18
= 954 + 180
= 1134.
Q1: Use this method to find the following products:
(a) 95 × 8
Ans: Write 95 as (100 – 5): 100 × 8 = 800
5 × 8 = 40
800 – 40 = 760
So, 95 × 8 = 760.
(b) 104 × 15
Ans: Write 104 as (100 + 4): 100 × 15 = 1500
4 × 15 = 60
1500 + 60 = 1560
So, 104 × 15 = 1560.
(c) 49 × 50
Ans: Write 49 as (50 – 1): 50 × 50 = 2500
1 × 50 = 50
2500 – 50 = 2450
So, 49 × 50 = 2450.
Q2: Is this quicker than the multiplication procedure you use generally?
Ans: Yes, this method can be quicker because it uses easier numbers like 100 or 50 and then adjusts with simple subtraction or addition, instead of doing long multiplication step by step.
Q4: Which other products might be quicker to find like the ones above?
Ans: Products like 98 × 25, 99 × 10, 103 × 15, or 51 × 50 might be quicker because they can be written as (100 – 2) × 25, (100 – 1) × 10, (100 + 3) × 15, or (50 + 1) × 50, and solved using the same easy method.
Figure it Out
Q1: Fill in the blanks with numbers, and boxes by signs, so that the expressions on both sides are equal.

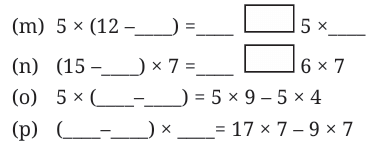
Ans: (a) 3 × (6 + 7) = 3 × 6 + 3 × 7
(b) (8 + 3) × 4 = 8 × 4 + 3 × 4
(c) 3 × (5 + 8) = 3 × 5 + 3 × 8
(d) (9 + 2) × 4 = 9 × 4 + 2 × 4
(e) 3 × (10 + 4) = 30 + 12
(f) (13 + 6) × 4 = 13 × 4 + 24
(g) 3 × (5 + 2) = 3 × 5 + 3 × 2
(h) (2 + 3) × 4 = 2 × 4 + 3 × 4
(i) 5 × (9 – 2) = 5 × 9 – 5 × 2
(j) (5 – 2) × 7 = 5 × 7 – 2 × 7
(k) 5 × (8 – 3) = 5 × 8 – 5 × 3
(l) (8 – 3) × 7 = 8 × 7 – 3 × 7
(m) 5 × (12 – 3) = 60 – 5 × 3
(n) (15 – 6) × 7 = 105 – 6 × 7
(o) 5 × (9 – 4) = 5 × 9 – 5 × 4
(p) (17 – 9) × 7 = 17 × 7 – 9 × 7
Q2: In the boxes below, fill ‘<’, ‘>’ or ‘=’ after analysing the expressions on the LHS and RHS. Use reasoning and understanding of terms and brackets to figure this out and not by evaluating the expressions.
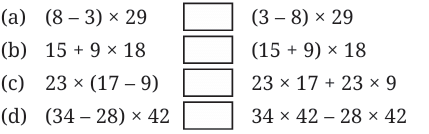
(a) (8 – 3) × 29 ___ (3 – 8) × 29
Ans: >
Explanation:
- (8 – 3) = 5, so left side is 5 × 29 = 145
- (3 – 8) = –5, so right side is –5 × 29 = –145
Since 145 is greater than –145,
145 > –145 ⇒ So, the answer is: >
(b) 15 + 9 × 18 ___ (15 + 9) × 18
Ans: <
Explanation:
- Follow BODMAS:
Left side → 9 × 18 = 162 → 15 + 162 = 177
Right side → (15 + 9) × 18 = 24 × 18 = 432
Since 177 < 432,
So, the answer is: <
(c) 23 × (17 – 9) ___ 23 × 17 + 23 × 9
Ans: =
Explanation:
This shows the distributive property:
23 × (17 – 9) = 23 × 8 = 184
Right side: 23 × 17 = 391, 23 × 9 = 207
391 + 207 = 598
Answer: = So, the answer is: <
(d) (34 – 28) × 42 ___ 34 × 42 – 28 × 42
Ans: =
Explanation:
Left side: (34 – 28) × 42 = 6 × 42 = 252
Right side: 34 × 42 = 1428, 28 × 42 = 1176 → 1428 – 1176 = 252
Both sides are equal.
Answer: =
Q3: Here is one way to make 14: _2_ × ( _1_ + _6_ ) = 14. Are there other ways of getting 14? Fill them out below:
(a) ___ × (___ + ___ ) = 14
Ans: 7 × (1 + 1) = 14
(b) ___ × (___ + ___ ) = 14
Ans: 2 × (5 + 2) = 14
(c) ___ × (___ + ___ ) = 14
Ans: 1 × (10 + 4) = 14
(d) ___ × (___ + ___ ) = 14
Ans: 14 × (1 + 0) = 14
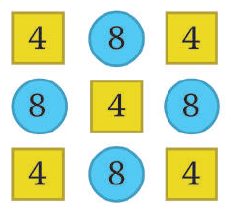
Q4: Find out the sum of the numbers given in each picture below in at least two different ways. Describe how you solved it through expressions.
Ans: Numbers: 4, 8, 4, 8, 4, 8, 4, 8, 4 (in a 3 × 3 grid)
First Way: Add all numbers one by one:
4 + 8 + 4 + 8 + 4 + 8 + 4 + 8 + 4 = 52
Second Way: Count how many 4s and 8s:
- There are 5 fours: 5 × 4 = 20
- There are 4 eights: 4 × 8 = 32
Add them: 20 + 32 = 52
So, the sum is 52.

Ans: Numbers: 5, 6, 6, 5, 6, 5, 5, 6, 6, 5, 5, 6, 5, 6, 6, 5 (in a 4 × 4 grid)
First Way: Add all numbers one by one:
5 + 6 + 6 + 5 + 6 + 5 + 5 + 6 + 6 + 5 + 5 + 6 + 5 + 6 + 6 + 5 = 88
Second Way: Count how many 5s and 6s:
- There are 8 fives: 8 × 5 = 40
- There are 8 sixes: 8 × 6 = 48
Add them: 40 + 48 = 88
Figure it Out
Q1: Read the situations given below. Write appropriate expressions for each of them and find their values.
(a) The district market in Begur operates on all seven days of a week. Rahim supplies 9 kg of mangoes each day from his orchard and Shyam supplies 11 kg of mangoes each day from his orchard to this market. Find the amount of mangoes supplied by them in a week to the local district market.
Ans:
- Expression for Rahim: 9 kg × 7 days
- Value for Rahim: 9 × 7 = 63 kg
- Expression for Shyam: 11 kg × 7 days
- Value for Shyam: 11 × 7 = 77 kg
- Total amount: 63 kg + 77 kg = 140 kg
(b) Binu earns ₹20,000 per month. She spends ₹5,000 on rent, ₹5,000 on food, and ₹2,000 on other expenses every month. What is the amount Binu will save by the end of a year?
Ans:
- Expression for monthly savings: ₹20,000 – (₹5,000 + ₹5,000 + ₹2,000)
- Monthly savings: ₹20,000 – ₹12,000 = ₹8,000
- Expression for yearly savings: ₹8,000 × 12 months
- Value for yearly savings: ₹8,000 × 12 = ₹96,000
(c) During the daytime a snail climbs 3 cm up a post, and during the night while asleep, accidentally slips down by 2 cm. The post is 10 cm high, and a delicious treat is on its top. In how many days will the snail get the treat?
Ans: In one day, the snail climbs 3 cm but slips down 2 cm at night.So, net gain in one day = 3 cm – 2 cm = 1 cm.
After 7 days, the snail climbs 7 cm (1 cm per day).
On the 8th day, the snail climbs up 3 cm, reaching from 7 cm to 10 cm.
This time, it reaches the top before slipping down, so it gets the treat.
The snail will get the treat in 8 days.
Q2: Melvin reads a two-page story every day except on Tuesdays and Saturdays. How many stories would he complete reading in 8 weeks? Which of the expressions below describes this scenario?
(a) 5 × 2 × 8
(b) (7 – 2) × 8
(c) 8 × 7
(d) 7 × 2 × 8
(e) 7 × 5 – 2
(f) (7 + 2) × 8
(g) 7 × 8 – 2 × 8
(h) (7 – 5) × 8
Ans: Number of days in a week except Tuesday and Saturday = 7 – 2
Since Melvin reads a two-page story every day except Tuesday and Saturday.
Therefore, number of stories read in a week = 1 × (7 – 2)
So, number of stories read in 8 weeks = 8 × 1 × (7 – 2)
= 8 × (7 – 2) or (7 – 2) × 8 [Expression (b)]
or 7 × 8 – 2 × 8 [Expression (g)]
Only expressions (b) and (g) describe this scenario.
Q3: Find different ways of evaluating the following expressions:
(a) 1 – 2 + 3 – 4 + 5 – 6 + 7 – 8 + 9 – 10
Ans: Way 1: Pair terms: (1 – 2) + (3 – 4) + (5 – 6) + (7 – 8) + (9 – 10) = -1 – 1 – 1 – 1 – 1 = -5.
Way 2: Add sequentially: 1 – 2 = -1, -1 + 3 = 2, 2 – 4 = -2, -2 + 5 = 3, 3 – 6 = -3, -3 + 7 = 4, 4 – 8 = -4, -4 + 9 = 5, 5 – 10 = -5.
Value: -5.
(b) 1 – 1 + 1 – 1 + 1 – 1 + 1 – 1 + 1 – 1
Ans: Way 1: Pair terms: (1 – 1) + (1 – 1) + (1 – 1) + (1 – 1) + (1 – 1) = 0 + 0 + 0 + 0 + 0 = 0.
Way 2: Add sequentially: 1 – 1 = 0, 0 + 1 = 1, 1 – 1 = 0, …, ending at 0.
Value: 0.
Q4: Compare the following pairs of expressions using ‘<‘, ‘>’ or ‘=’ by reasoning.
(a) 49 – 7 + 8 __ 49 – 7 + 8
Ans: Same expression.
So, 49 – 7 + 8 = 49 – 7 + 8.
(b) 83 × 42 – 18 __ 83 × 40 – 18
Ans: 83 × 42 = 83 × (40 + 2) = 83 × 40 + 83 × 2.
So, 83 × 42 – 18 > 83 × 40 – 18.
(c) 145 – 17 × 8 __ 145 – 17 × 6
Ans: 17 × 8 = 136, 17 × 6 = 102. 145 – 136 < 145 – 102.
So, 145 – 17 × 8 < 145 – 17 × 6.
(d) 23 × 48 – 35 __ 23 × (48 – 35)
Ans: 23 × 48 – 35 > 23 × 13 (since 48 > 13).
So, 23 × 48 – 35 > 23 × (48 – 35).
(e) (16 – 11) × 12 __ -11 × 12 + 16 × 12
Ans: (16 – 11) × 12 = 5 × 12. -11 × 12 + 16 × 12 = (16 – 11) × 12 = 5 × 12.
So, (16 – 11) × 12 = -11 × 12 + 16 × 12.
(f) (76 – 53) × 88 __ 88 × (53 – 76)
Ans: (76 – 53) = 23, (53 – 76) = -23.
So, 23 × 88 > -23 × 88.
Therefore, (76 – 53) × 88 > 88 × (53 – 76).
(g) 25 × (42 + 16) __ 25 × (43 + 15)
Ans: 42 + 16 = 58, 43 + 15 = 58.
So, 25 × (42 + 16) = 25 × (43 + 15).
(h) 36 × (28 – 16) __ 35 × (27 – 15)
Ans: 28 – 16 = 12, 27 – 15 = 12.
But 36 > 35.
So, 36 × (28 – 16) > 35 × (27 – 15).
Page No. 44
Q5: Identify which of the following expressions are equal to the given expression without computation. You may rewrite the expressions using terms or removing brackets. There can be more than one expression which is equal to the given expression.
(a) 83 – 37 – 12
(i) 84 – 38 – 12
(ii) 84 – (37 + 12)
(iii) 83 – 38 – 13
(iv) – 37 + 83 –12
(b) 93 + 37 × 44 + 76
(i) 37 + 93 × 44 + 76
(ii) 93 + 37 × 76 + 44
(iii) (93 + 37) × (44 + 76)
(iv) 37 × 44 + 93 + 76
Ans: (a) The expressions equal to 83 – 37 – 12 are:
(i) 84 – 38 – 12 (because 84 – 38 = 46 and 46 – 12 = 34, same as 83 – 37 – 12 = 34)
(ii) 84 – (37 + 12) (because 37 + 12 = 49, and 84 – 49 = 35,
but this is incorrect; correct check: 84 – 49 = 35, not 34, so only (i) and (iv) work)
(iv) –37 + 83 – 12 (because –37 + 83 = 46, and 46 – 12 = 34)
(b) The expressions equal to 93 + 37 × 44 + 76 are:
(iv) 37 × 44 + 93 + 76 (same order of operations)
Q6: Choose a number and create ten different expressions having that value.
Ans: Let’s choose the number 10. Ten different expressions are:
- 5 + 5
- 20 – 10
- 2 × 5
- 50 ÷ 5
- 15 – 5
- 7 + 3
- 4 × 2 + 2
- 30 – 20
- 10 × 1
- 25 – 15