Textbooks solutions
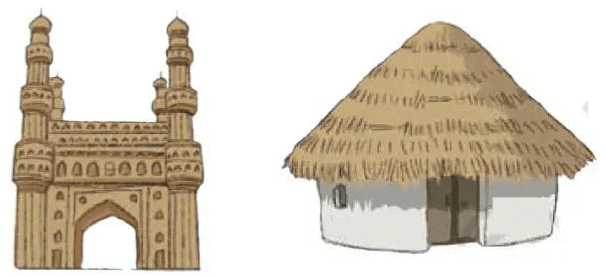

Shapes and Models(Page 1)Try to make a model of the buildings shown here using blocks.

Q1: What parts of the building have you shown in your model (for example, roof, pillars, base, etc.)?
Ans: I have shown the base, pillars, sidewalls, and roof of the building in my model.
Q2: Why did you select these parts?
Ans: I have selected these parts because they form the core structure of the building.
Q3: What shapes will model these parts well?
Ans: Rectangles, squares, semicircles, and cylinders are the shapes that model these parts well
Q4: How is your model similar to the picture of the real building?
Ans: The shapes of the different parts of my model closely match those of the real building in the picture.
Q5: How is it different from the real building?
Ans: My model is smaller, made of blocks, and does not have details like carvings of the real India Gate.
Discussion:
- What would happen if you removed one piece of your model?
Ans: The model might become unstable or look incomplete. - Would the model still look like the original building?
Ans: No, the model won’t look like the original building. - In what ways could you make the model even better?
Ans: To make the model even better, I could paint it in colours that closely resemble the actual building.
Project Work(Page 2)

Q1: Do you think it looks like the Qutub Minar?
Ans: No, it doesn’t look like the Qutub Minar.
Q2: What shape would you use if you made a model of the Qutub Minar? Why?
Ans: I would use a cylindrical shape to make a model of the Qutub Minar because the actual structure is tall and round, similar to a cylinder.
Q3: How many such shapes will you use?
Ans: I would use five cylindrical shapes to make different levels of the Qutub Minar in my model.


Ans:

Craft(Page 3 & 4)Q1: Make a sphere-like shape with paper strips.
Ans:
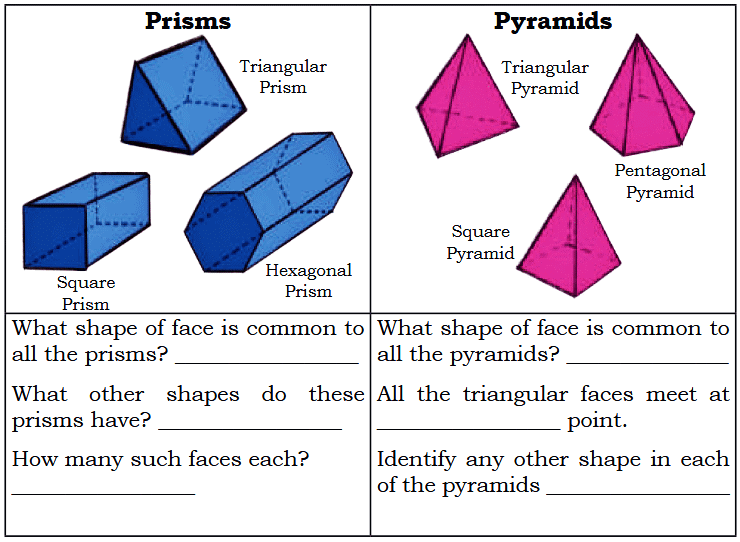
Q2: Use the nets given at the end of the book to make the models shown below.
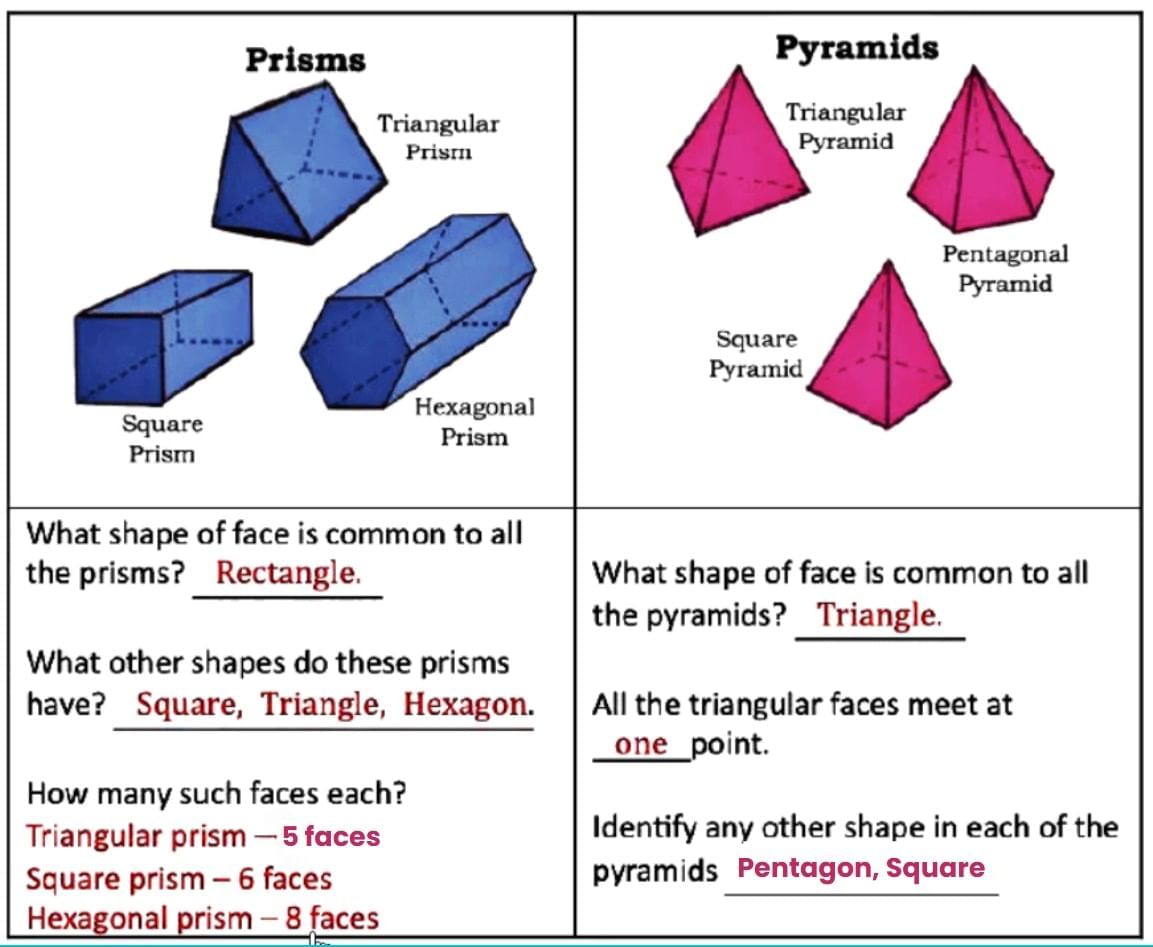
Ans:
- Is a cube also a prism?
Ans: Yes, a cube is a special type of prism where all faces are squares and all edges are of equal length. - What is the difference between a prism and a pyramid?
Ans: A prism has two identical bases while a pyramid has one base. Also, a prism has all rectangular or parallelogram-shaped side faces while a pyramid has all triangular side faces.
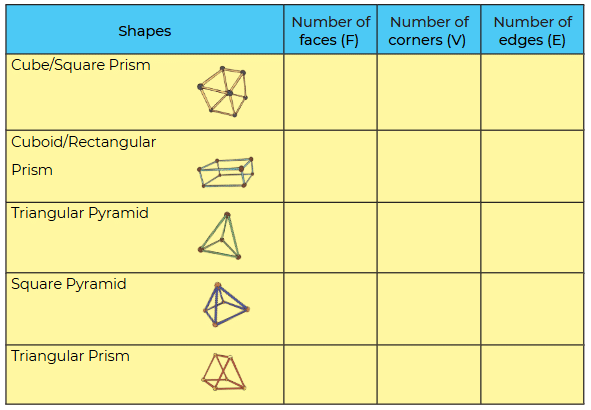
Q: Now try to make the above shapes using straws and plasticine/ thread and fill in the table.
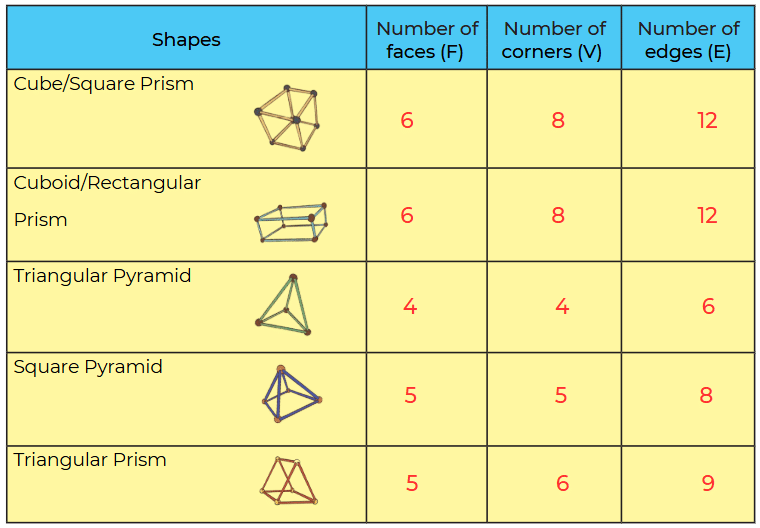
Ans:
Q: Identify any relationship that you may find between the number of faces (F), edges (E), and corners (V). Calculate F+V-E in each case. What do you notice?
Ans: The formula says: F + V – E = 2
Where:
- F = Faces
- V = Vertices (corners)
- E = Edges


Here are the calculations:
1. Cube (Square Prism):
F + V – E = 6 + 8 – 12 = 2
2. Cuboid (Rectangular Prism):
F + V – E = 6 + 8 – 12 = 2
3. Triangular Pyramid:
F + V – E = 4 + 4 – 6 = 2
4. Square Pyramid:
F + V – E = 5 + 5 – 8 = 2
5. Triangular Prism:
F + V – E = 5 + 6 – 9 = 2
What we notice?
In every case, F + V – E = 2!Ans:
Q: Can you construct a 3D shape with 3 flat faces?
Ans: No, it is impossible to construct a 3D shape with 3 flat faces.


Ans:


Let Us Observe(Page 5)Q1: Take a die. Look at the face that has number 1. The face numbered 6 is opposite to the face numbered 1.
What is the face opposite to the:
(a) face numbered 2? ……….
(b) face numbered 3? ……….
(c) face numbered 4? ……….
Ans: Numbers on opposite faces of a die always add up to 7. Therefore:
Q2: (a) Which faces have common edges with the face numbered 1?………..
(b) Which face has no common edge with the face numbered 1?………..
Ans: a) Faces having common edges with the face numbered 1 are 2, 3, 4 & 5.
b) Faces having no common edges with the face numbered 1 is 6.
Q3: Look at three different views of the same cube.
(a) What colour is the face that is opposite to the red face? …………
Ans: a) Colour of face opposite to red face – Purple.
(b) What colour is the face that is opposite to the yellow face?……….
Ans: b) Colour of face opposite to yellow face-Green.


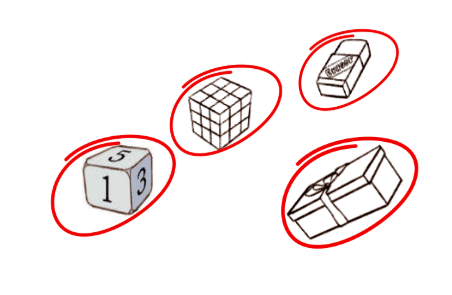
Follow these instructions for the shapes along the border.Q1: Colour all shapes with a rectangular face in red.
Ans: Colour the cube, cuboid, and rectangular prism in red.
Q2: Draw a smiley on shapes with a triangular face.
Ans: Draw a smiley on the triangular prism and triangular pyramid.
Q3: Draw a star on shapes with a curved face.
Ans: Draw a star on the cylinder, cone, and sphere.
Q4: Colour all shapes with no corner in blue.
Ans: Colour the sphere and cylinder in blue.
Q5: Circle the shapes that have the same opposite faces.
Ans: Circle the cube and cuboid, as their opposite faces are identical.
Sorting 3D Shapes(Page 6)
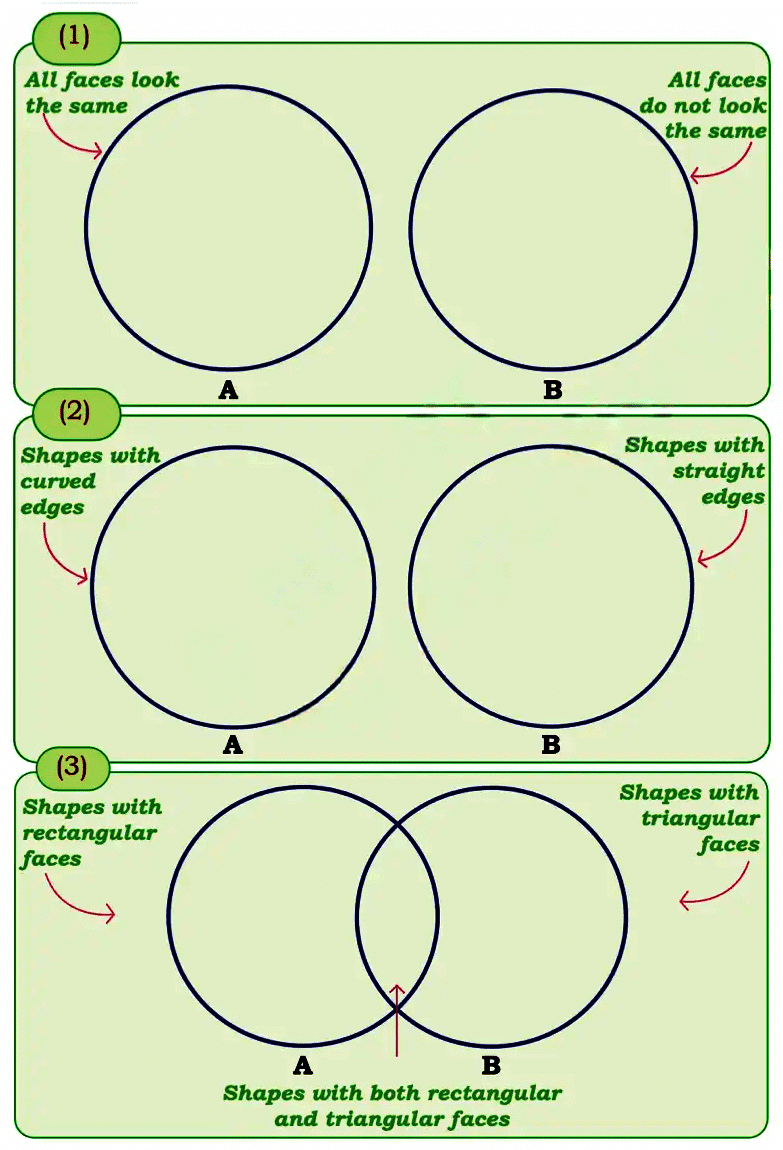
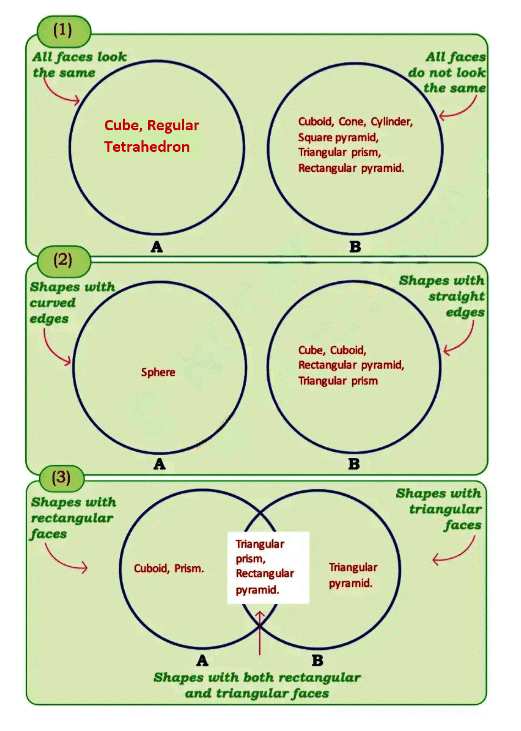
Write the names of 3D shapes in the correct places.
Ans:

Q: In which circle did you write triangular prism and rectangular pyramid?
Ans: Triangular prism and rectangular pyramid are written in circle 1(B), Circle 2(B) and intersection of circles 3(A) and 3(B).
Let us sort shapes in another way.
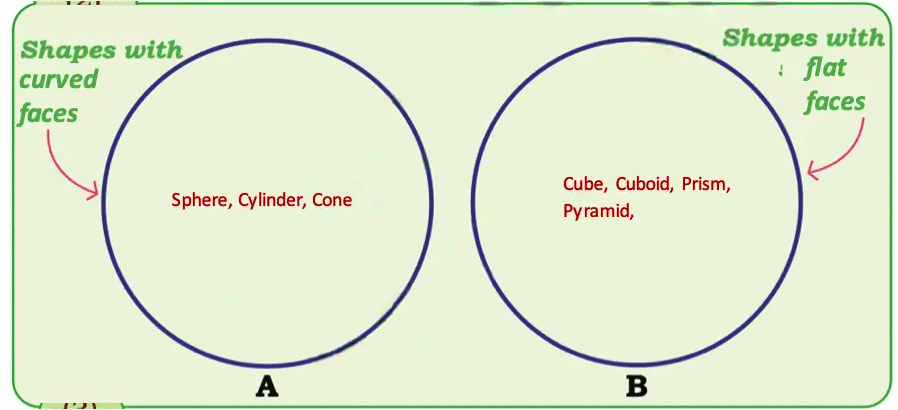
Q: Using circles like those on the previous page, can you sort shapes into the categories “Shapes with curved faces” and “Shapes with flat faces” ?
Ans:
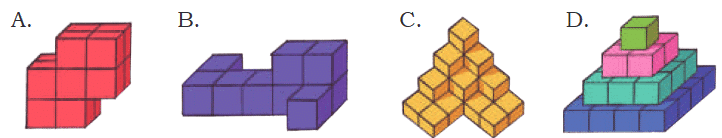
Build with Cubes(Page 7)Q: Build these models with the cubes from the Jaadui Pitara Kit or any other similar material.
Ans: Do it Yourself.
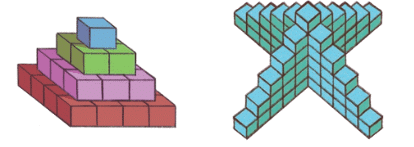
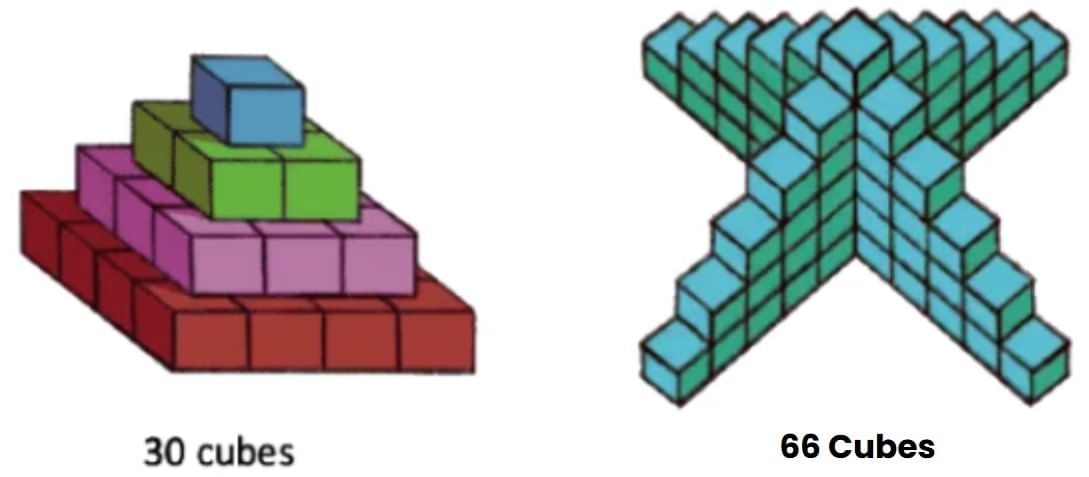
Cube TowersQ1: How many cubes are there in each of these cube towers?Ans:
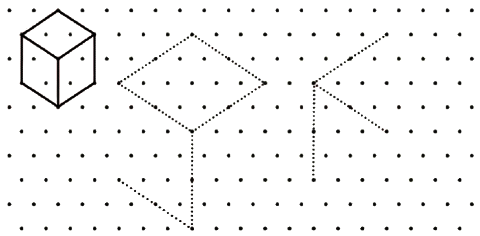
Drawing Cubes on a Triangular Dot Paper(Page 8)Q: Can you complete the following cubes?
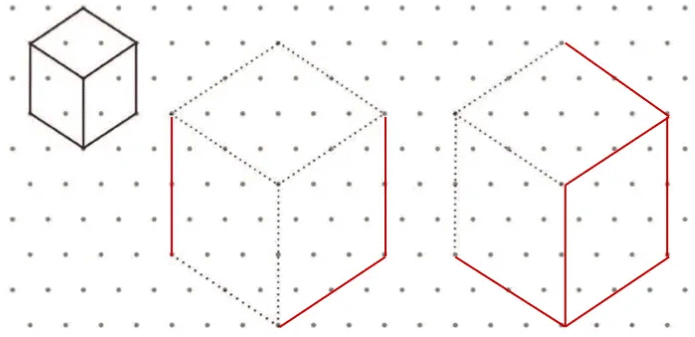

Ans: Q:

Ans:

Q2: Each one is different. How?Ans:
- Sphere (Red Ball)
It has no flat faces, no corners, and is completely round. - Cone (Golden)
It has 1 flat face (circle) and 1 curved face. - Triangular Pyramid (Blue)
It has 4 triangular faces. - Cube (Green)
All faces are equal squares. It has 6 faces, 8 corners, and 12 straight edges. - Cuboid (Purple)
It looks like a box. Faces are rectangles, not all the same like a cube. It also has 6 faces, 8 corners, and 12 edges.
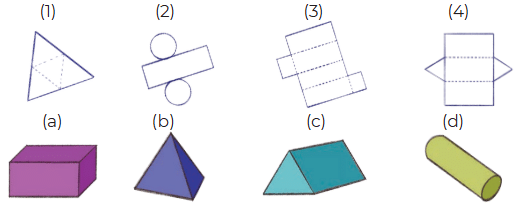
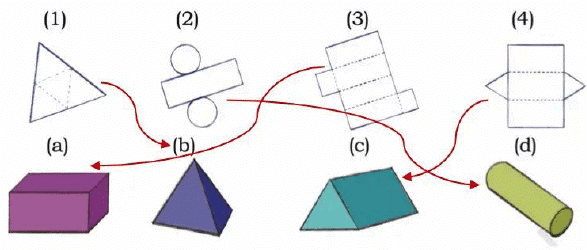
Q3: Match the following nets to the appropriate solids.Ans:
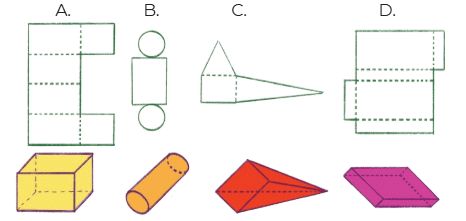


Q4: Which of these nets can be folded to make a solid of the kind given below?Ans: Net B and D can be folded to make a solid shapes.
Q5: Nitesh cuts up a net on the folds. Here are its pieces.
Which solid has the above pieces in its net?
(a)



(b)
(c)
(d)
Ans: The solid is (d)
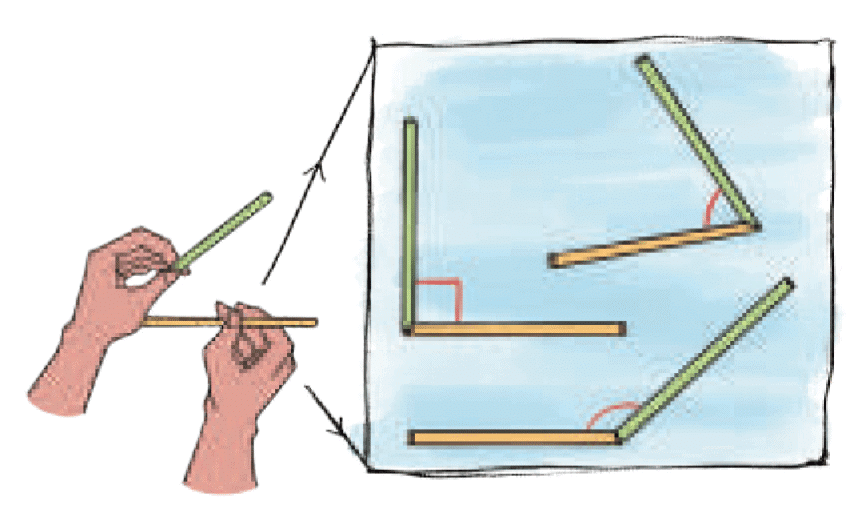

When Lines Meet(Page 10)Isha made different corners with straws. We can say that the two straws are like two lines that meet at a point.
When two lines meet they create an angle.
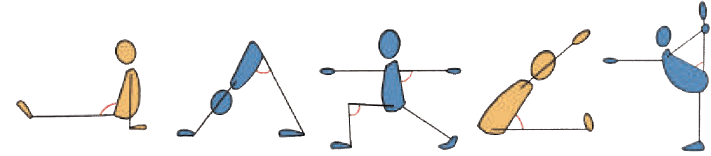
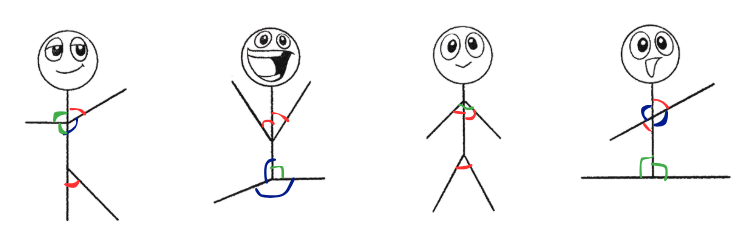
We see many angles in yoga postures.
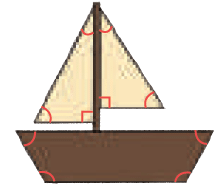
There are 7 angles in this house drawing.
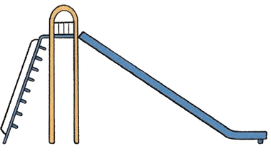
How many angles are there in this boat drawing?
Ans: There are 10 angles in the boat drawing. These angles are formed where the lines of the boat’s hull, sail, and mast meet.

Let Us DoQ1: Mark the angles in the following pictures.
(a)


(b)
(c)
(d)
(e)
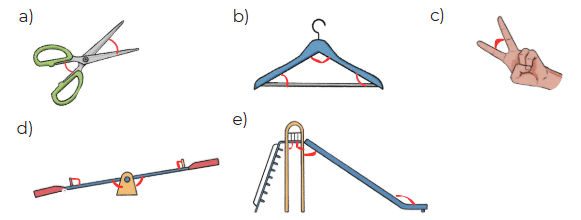
Ans: Mark the angles where lines meet in each picture (e.g., corners of shapes or intersections).
Q2: Where do you see angles in the classroom? Give a few examples.
Ans: Angles can be seen in many places around the classroom. They are present in the corners of desks, chairs, tables, windows, doors, cupboards, and even in the whiteboard or chalkboard.
Right Angles(Page 11)
Q: Let’s make a right angle with a piece of paper as shown.
Ans: Do it Yourself.
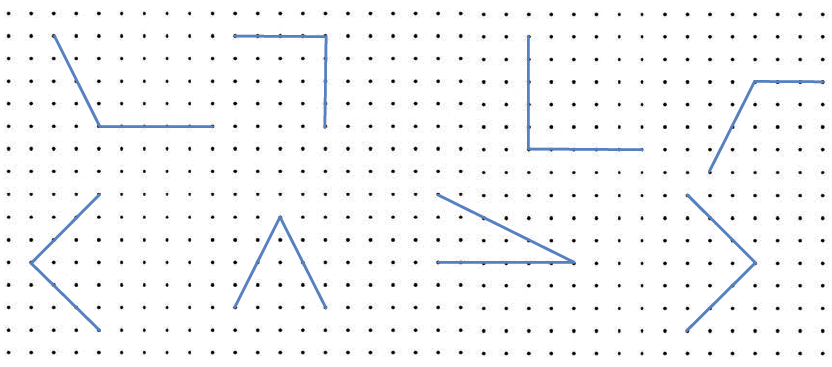
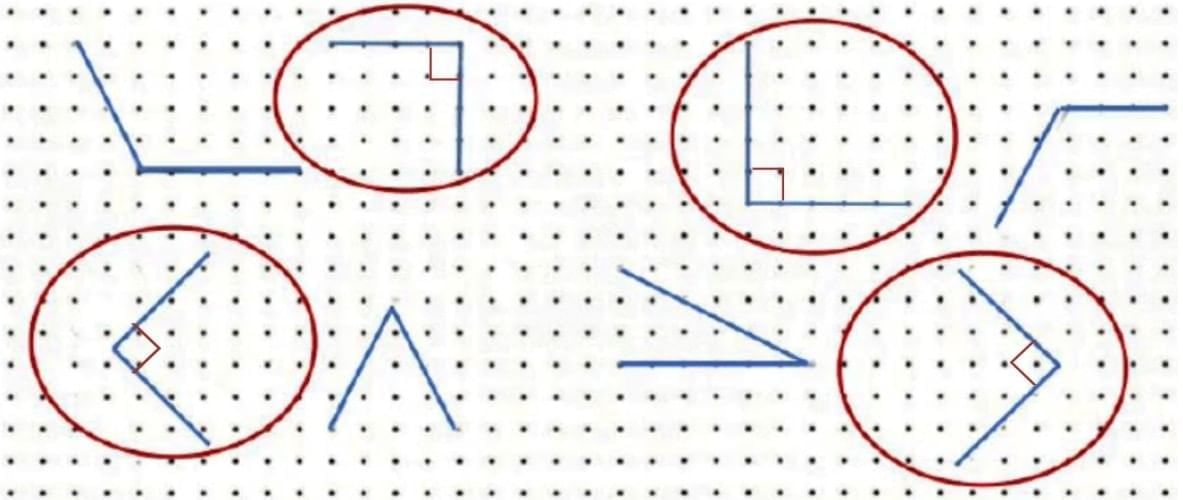
Q: Identify the angles that you think are right angles and circle them in the dot grid given below. Check using your right angle checker.
Ans:
Q: Check for right angles in a book, window, and any other object. Write the names of objects where you find right angles.
Ans: Angles can be found in objects such as windows, doors, chairs, whiteboards/blackboards, books, desks, etc.

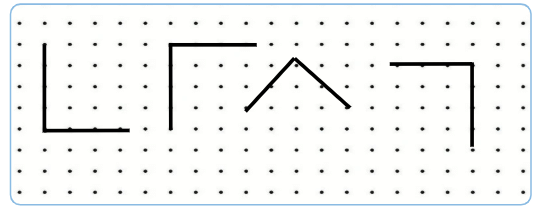
Let Us DoPage 12Q: Draw some right angles on the dot grid.
Ans:

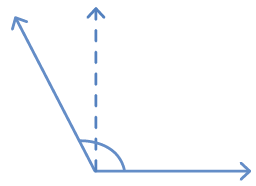
Acute and Obtuse AnglesAcute angles are less than a right angle.
Obtuse angles are more than a right angle.

Q: Name some objects from your classroom which have an acute angle.
Ans: Scissors, pencil tip, corner of a triangle ruler.
Q: Name some objects from your classroom which have an obtuse angle.
Ans: Open laptop, chair backrest, open door, open notebook.
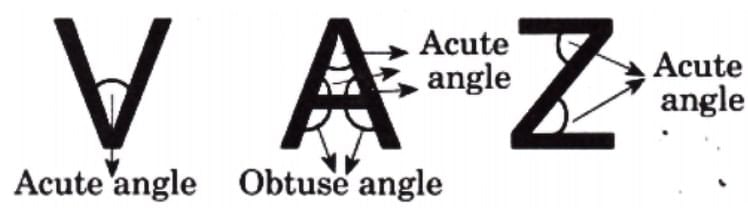
Q: Identify all angles in the following letters.
Ans:

Let Us Do(Page 13) Q:
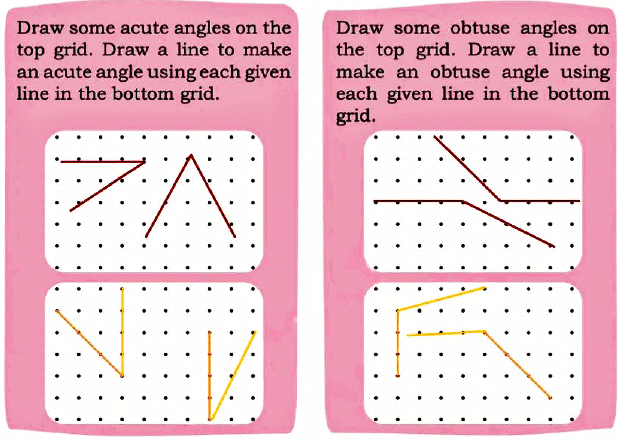
Ans:
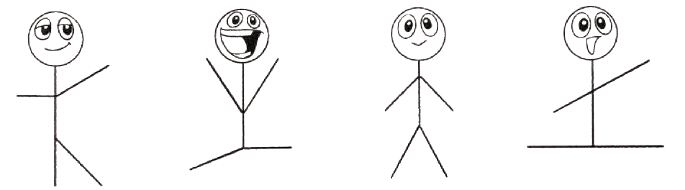
Q2: In the figures given below, mark the acute angles in red, right angles in green, and obtuse angles in blue.
Ans: Color angles based on their size:
- Acute (less than 90°): Red
- Right (90°): Green
- Obtuse (more than 90°): Blue
Shapes with Straws(Page 14)
Q: Make a triangle with straws of different sizes and clay/ plasticine.


Q1: Does the shape of the triangle change if we gently push one of its sides? (Yes/No)
Ans: Yes.
Q2: What kinds of angles does a triangle have?
Ans: A triangle can have: (i) All three acute angles. (ii) One right angle and two acute angles. (iii) One obtuse angle and two acute angles.
Q3: What kinds of angles do you see in the rectangle?
Ans: A rectangle has four right angles.
Does the shape of the rectangle change if we gently push one of its sides? (Yes/No)
Ans: Yes.
- What has happened to the angles of the new shape?
Ans: The measure of the angles have changed. - Are they still right angles? What types of angles have been formed?
Ans: No, they are not right angles. Acute and obtuse angles are formed. - Similarly, push one side of a square. Are they still right angles? What types of angles have been formed?
Ans: No, they are not right angles. Acute and obtuse angles are formed. - How are the angles of triangles and rectangles similar or different?
Ans: Similarities: Both triangles and rectangles can contain right angles.
Differences: A triangles has three angles while a rectangle has four angles.
All four angles in a rectangle are right angles while a triangle can have zero or one right angle.

Dot Grid(Page 15)Use the dot grid given below to draw several three- and four-sided shapes. Circle the shapes that have one or more right angles.
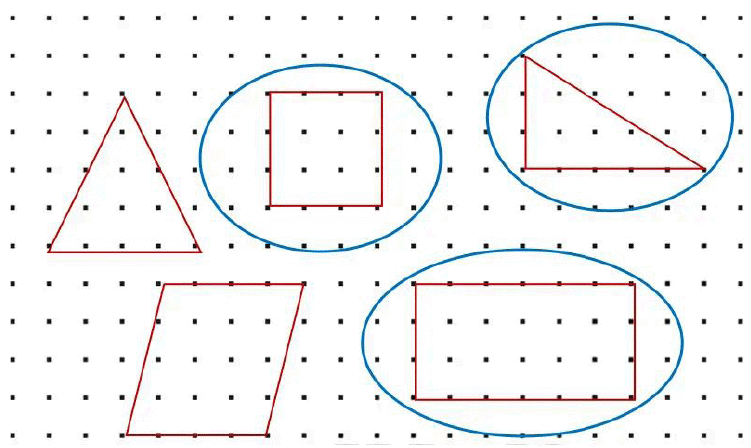
Ans:
DiscussQ1: What shapes did you make?
Ans: I made two triangles, a square, a rectangle and a parallelogram.
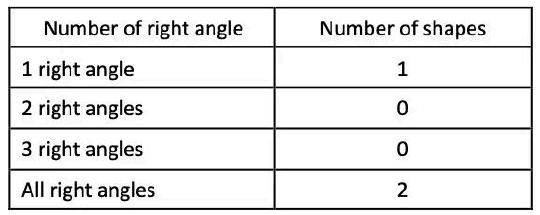
Q2: How many shapes have you made with:
(a) 1 right angle
(b) 2 right angles
(c) 3 right angles
(d) all right angles
Ans:
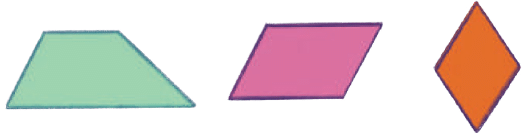
Q3: Here are some 4-sided shapes. In what ways are rectangle and square different from these shapes?
Ans: Rectangles and squares both have four right angles, whereas each of these shapes are formed by a combination of acute and obtuse angles.
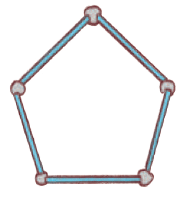
Activity(Page 16)
Try to make this 5-sided shape with all sides equal (Pentagon)
Q1: Are these right angles?
Ans: No, the angles in a regular pentagon are obtuse (108 degrees).
Q2: Does the shape of the pentagon change if we gently push one of its sides?
Ans: Yes.
Q3: How does this change the angles?
Ans: On being gently pushed, the pentagon shows a combination of acute and obtuse angles.
Can you make a circle using straws?Q: Look at the picture. The lengths of the straws in this picture are ……………..(Equal/Unequal)
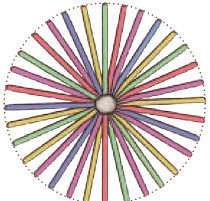
Ans: Equal
Q: What will happen if we take straws of unequal lengths?
Ans: The resultant shape formed will not be a circle.

Let Us Make(Page 16)Can you use a scale to draw a circular shape? Let us see.
Mark a point A.
Draw many points that are at an equal distance from point A. Connect the dots freehand. What do you get?
Ans: A circle
Amazing Circles(Page 17)

Q1: The length of all the creases are_________ (Equal/Unequal)?
Ans: Equal.
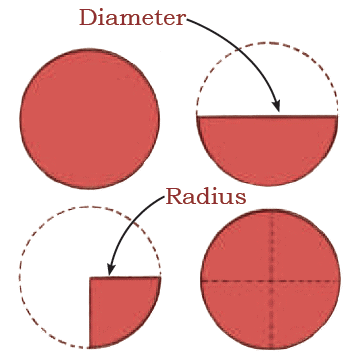
Q2: These creases are called diameters of the circle.
Q3: Discuss where the centre is. Do you notice that all the diameters pass through the centre?
Ans: The centre is the point where all diameters meet. Yes, all diameters pass through the centre.
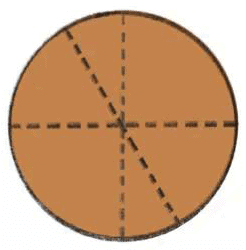
Q4: Measure the length of the creases from the center to the border of the circle. This is called the radius of the circle.
Q5: Discuss if there is any relationship between the radius and the diameter of a circle.
Ans: Diameter is twice the radius of the circle.
Let Us Do(Page 18)Fold the circular paper in half.
Fold this half again in half.

Q: The length of the diameter is __________(half/double) of the length of radius.
Ans: double
Q: A circle can be made easily using a compass. Ask your teacher to help you use a compass. Make the following design.

Ans: Do Yourself.
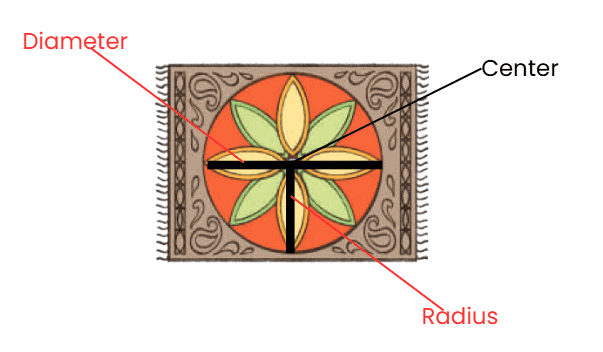
Q: Look at the carpet design. A beautiful circle, right? Mark the centre, radius, and the diameter of the circular design with any colour of your choice.
Ans:

The Wheels(Page 19)Look at the wheels.
All wheels look like circle.
Name the wheel with the
1. longest radius_______
Ans: longest radius B
2. shortest radius______
Ans: shortest radius D
3. longest diameter______
Ans: longest diameter B
4. shortest diameter_______
Ans: shortest diameter D
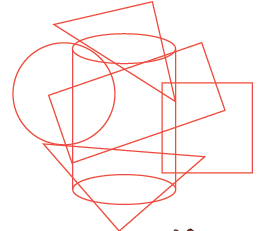
Puzzling ShapesQ1: Identify the hidden shapes and write their names.
Ans: Triangle, cylinder, circle, rectangle, square.
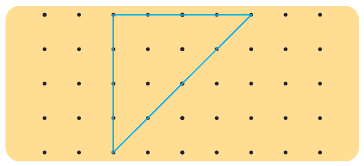
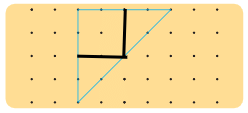
Q2: Draw 2 lines to divide the triangle into 1 square and 2 triangles.
Ans:
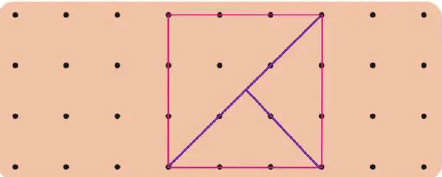
Q3: Draw 2 lines to divide the square into 3 triangles.
Ans:
Q4: Draw lines to show the cuts needed on the shapes in the left column to get the smaller shapes on the right.
Ans:

Card Game(Page 20)Sort the 2D-shape cards given at the end of the book into three groups according to their sides.
Q: Draw the sorted shapes in the space given below. Explain why you sorted your shapes in this way.
Ans:
Let Us Try(Page 21)1. Squiggly spiders
Squiggly, the spider, likes to make webs in different shapes. One day she begins to make triangular webs.
How many triangles are in her web?
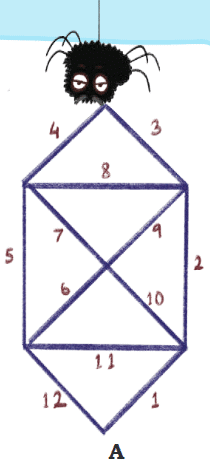
Ans: Number of triangles in her web = 10.
She likes to take a walk each morning and check if the walls of her web are strong.
Can she begin at point A and reach back to the same point without walking on any wall more than once?
Trace and show Squiggly’s path.
Ans: Yes, she can begin at point A and reach back to the same point without walking on any wall more than once.
Squiggly’s path = 1 → 2 → 3 → 4 → 8 → 9 → 6 → 11 → 10 → 7 → 5 → 12.
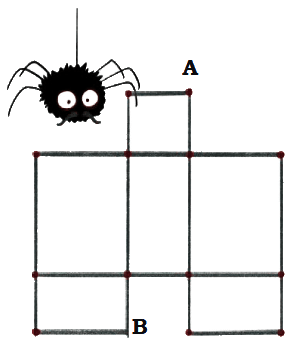
Her brother, Wiggly, made a web using rectangles.
How many rectangles can you see in his web?

Ans: Number of rectangles in his web = 12.
He likes to take a walk at the end of each day and check if the walls of his web are strong.
Can he begin at point A and leave from point B without walking on any wall more than once?
Trace and show Wiggly’s path.
Ans: No, Wiggly cannot start from A and leave from B without walking on any walls more than once and also go through all the walls.an once.
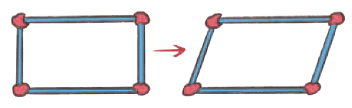
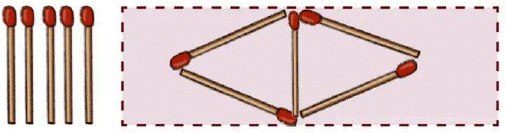
Q2: Use 5 matchsticks to make 2 triangles. Then draw it in the space provided.
Ans:
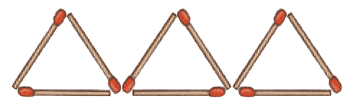

Q3: Move two of these matchsticks to form 4 triangles.
Ans:
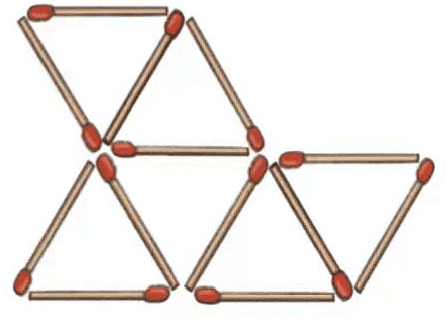
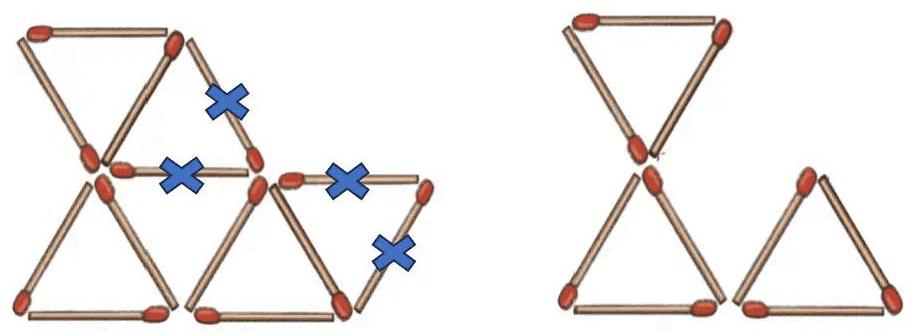
Q4: Remove 4 of these matchsticks to leave only 3 triangles.
Ans:
Q5: Model Challenge
Can you make a model of solid shapes which has:
(a) 12 straws and 8 clay balls?
(b) 9 straws and 6 clay balls?
(c) 15 straws and 10 clay balls?
(d) 10 straws and 6 clay balls?
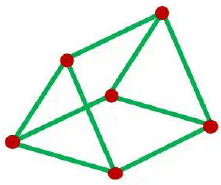
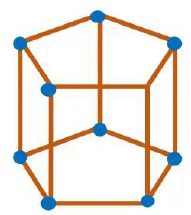
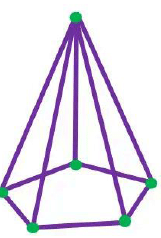
Ans: (a) Cuboid (12 straws and 8 clay balls).
b) Triangular prism (9 straws and 6 clay balls).
c) Pentagonal prism (15 straws and 10 clay balls)
d) Pentagonal pyramid (10 straws and 6 clay balls)
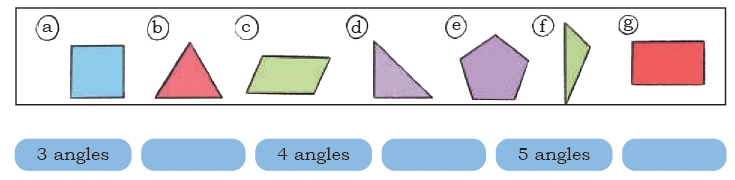
Q6: Classify these shapes based on the number of angles:
What relation do you notice between the number of sides and the number of angles?
Ans: Shapes with 3 angles – b, d, f.
Shapes with four angles – a, c, g.
Shapes with five angles – e.
Each shape has equal number of sides and angles.
Let Us Try(Page 23)Q7:
Ans:


Q8: Mark the right angles and write the number of right angles in each figure.
Which of the above shapes have only right angles?
Ans:
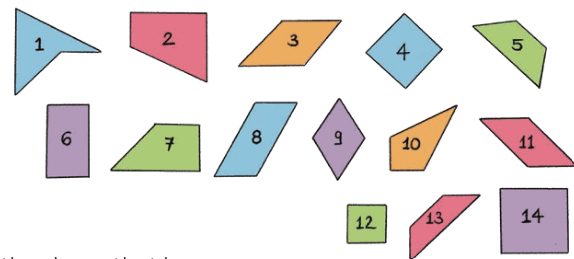
Q9: Observe the following shapes.
Identify the shape that has:
- 2 right angles, 1 acute, and 1 obtuse angle________
- 1 right, 2 obtuse, and 1 acute angle_________
- 2 obtuse, and 2 acute angles_________
- 4 right angles_________
Ans:
- 2 right angles, 1 acute, and 1 obtuse angle 2,7
- 1 right, 2 obtuse, and 1 acute angle 10
- 2 obtuse, and 2 acute angles 3,5,8,9,11,13
- 4 right angle 4, 6, 12, 14.