Page 34: Let Us Count

Gundappa has some land with tall coconut trees.
Q1: How many coconut trees does Gundappa have?
Ans: Gundappa has 81 coconut trees.
Q2: How do you know?
Ans: I counted the number of trees in each row and each column. There are 9 rows and 9 columns. So, the total number of trees is 9 × 9 = 81.
Q3: Gundappa has plucked 5 coconuts from each tree. How many coconuts has he plucked?
Ans: Gundappa has plucked 81 × 5 = 405 coconuts.
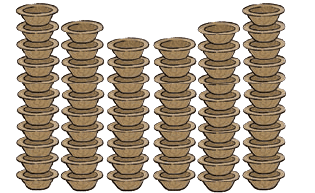
Q4: Muniamma makes plates and cups.
Number of cups = ________
Ans: In the first stack, from top to bottom, there are 11 cups. Similarly, in the second, third, fourth, fifth and sixth stacks, there are 10, 9, 9, 10 and 11 cups, respectively.
So, the total cups are:
11 + 10 + 9 + 9 + 10 + 11 = 60 cups
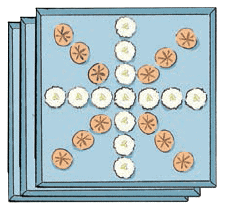
Muniamma has arranged coconut laddoos and milk peda in trays like this. All trays have the same arrangement. Trays are placed one on top of the other.
Q5: How many coconut laddoos are there in the trays?
Ans: Each tray has 13 coconut laddoos. There are 3 trays.
So, 13 × 3 = 39 coconut laddoos.
Q6: How many milk pedas are there in the trays?
Ans: Each tray has 12 milk pedas. There are 3 trays.
So, 12 × 3 = 36 milk pedas.Page 35: Patterns with Money
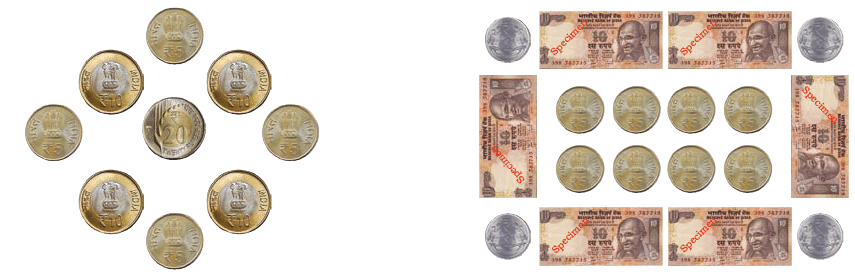
Shirley and Shiv arranged their play money in some nice patterns as shown below.
Q1: How much money? (Left pattern)
Ans: ₹80
Q2: How much money? (Right pattern)
Ans: ₹108
Q3: How did you count them?
Ans: Left Pattern:
There are 4 coins of ₹10 and 1 coin of ₹20 and 4 coins of ₹5.
So, total money = (4 × 10) + 20 + (5 x 4)= ₹80.
Right Pattern:
₹2 coins = 4
₹5 coins = 8
₹10 notes = 6
So, total money = (4 × 2) + (8× 5) + (6 × 10) = 8 + 40 + 60 = ₹108.
Q4: Arrange play money of amounts ₹1, ₹2, ₹5, and ₹10 to show ₹36, ₹125, and ₹183. Ask your peers to tell how much it is.
Ans:To make ₹36:
- ₹10 notes × 3 = ₹30
- ₹5 coin × 1 = ₹5
- ₹1 coin × 1 = ₹1
- Total = ₹30 + ₹5 + ₹1 = ₹36
To make ₹125:
- ₹10 notes × 10 = ₹100
- ₹5 coin × 5 = ₹25
- Total = ₹100 + ₹25 = ₹125
To make ₹183:
- ₹10 notes × 15 = ₹150
- ₹5 coin × 5 = ₹25
- ₹2 coin × 4 = ₹8
- Total = ₹150 + ₹25 + ₹8 = ₹183
Page No 35: Two Ways
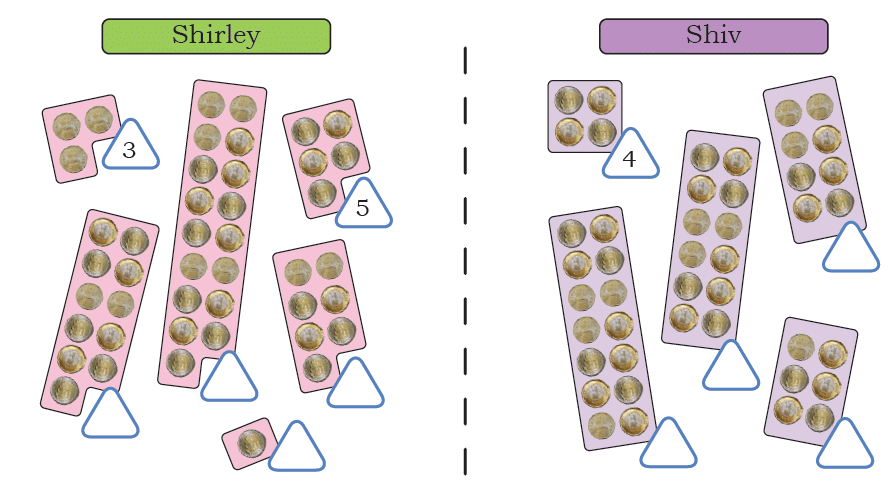
Shirley and Shiv arranged their coins in the following ways. Write the number of coins in the triangles.
Ans:
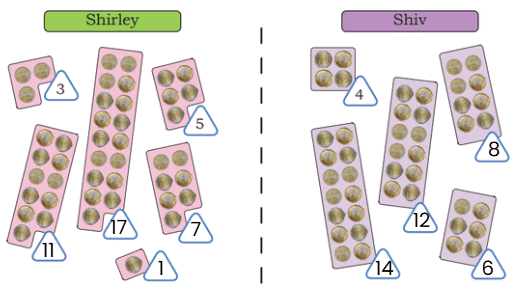
Q1: Describe Shiv’s arrangement and write his numbers.
Ans: Shiv has arranged his coins in even numbers. The numbers are 4, 6, 8, 12 and 14.
Q2: Describe Shirley’s arrangement and write her numbers.
Ans: Shirley has arranged her coins in odd numbers. The numbers are 1, 3, 5, 7, 11 and 17.
Q3: Identify numbers between 1 and 20 as even or odd. You may draw the pairing arrangement of the numbers.
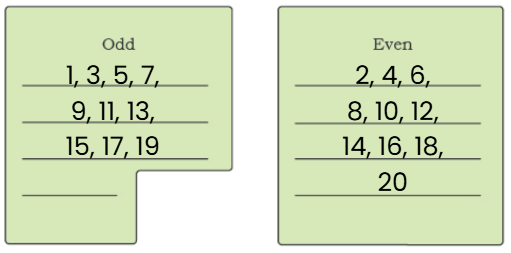
Ans: Odd numbers between 1 and 20: 1, 3, 5, 7, 9, 11, 13, 15, 17, 19
Even numbers between 1 and 20: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20
We can pair even numbers equally. Odd numbers always leave one unpaired.
Q4: Do you think all numbers in the times-2 table are even?
Ans: Yes, all numbers in the 2 times table are even.
For example: 2, 4, 6, 8, 10, 12… All these can be made into equal pairs without any left.Page 37: Crayons Arrangement
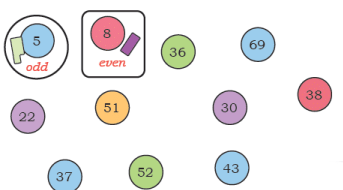
Q: Circle the odd numbers and put a square around each even number. Use the crayons arrangement, if needed.
Ans: The numbers given are 36, 37, 38, 39, 8, 5, 51, 52, 43, 69.
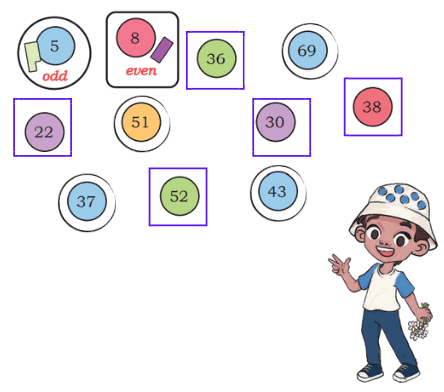
To check, pair crayons for each number. For example, 37 crayons leave one unpaired (odd), while 38 crayons can be fully paired (even).
Q: Explore your textbook and find out what Shirley has seen. Draw a square on the even numbers. Put a circle on the odd numbers.
Ans: Do it yourself.Page 38 – Crayons Arrangement (Continued)

Q: Identify which of the following numbers are even and which are odd. Explain your reasoning.
Ans: Even numbers: 30, 46, 78, 300, 154.
- Reasoning: These numbers can be paired completely. For example, 30 can be divided into 15 pairs (30 ÷ 2 = 15), so it is even.
Odd numbers: 67, 415, 99.
- Reasoning: These numbers cannot be paired completely. For example, 67 leaves one unpaired (67 ÷ 2 = 33 with remainder 1), so it is odd.
Q: Make two 2-digit numbers using the digits 1 and 6 without repetition. Identify the numbers as even or odd.
Ans:
- Numbers: 16, 61.
- 16 is even (can be paired, 16 ÷ 2 = 8).
- 61 is odd (cannot be paired, 61 ÷ 2 = 30 with remainder 1).
Q: Now choose any two digits and make 2-digit numbers in such a way that the numbers are even.
Ans: Choose digits 2 and 4.
- Numbers: 24, 42.
- Both are even: 24 ÷ 2 = 12 (paired), 42 ÷ 2 = 21 (paired).
Q: Are there more even or odd numbers between 1 and 100?
Ans: There are 50 even numbers and 50 odd numbers between 1 and 100.
- Even numbers: 2, 4, 6, …, 100 (50 numbers).
- Odd numbers: 1, 3, 5, …, 99 (50 numbers).
So, there are an equal number of even and odd numbers.
Q: Shirley notices that both the numbers, before and after an odd number, are even.
Ans: This is true. For example, for the odd number 5, the number before (4) and after (6) are even. Odd numbers (e.g., 1, 3, 5, …) are not divisible by 2, while the numbers before and after (e.g., 4 and 6 for 5) are divisible by 2, making them even.
Q: Shiv wonders if both the numbers, before and after an even number, will be odd. What do you think? Check and discuss.
Ans: Yes, this is true. For example, for the even number 4, the number before (3) and after (5) are odd. Even numbers (e.g., 2, 4, 6, …) are divisible by 2, while the numbers before and after (e.g., 3 and 5 for 4) are not divisible by 2, making them odd.

Q: Choose any 10 numbers in order without skipping any (consecutive numbers). Write whether they are even or odd below each number. What do you notice? Discuss.
Ans: Choose numbers 20 to 29:
- 20 (even), 21 (odd), 22 (even), 23 (odd), 24 (even), 25 (odd), 26 (even), 27 (odd), 28 (even), 29 (odd).
- Notice: The numbers alternate between odd and even (even, odd, even, odd, even, …). This happens because each number increases by 1, switching between not divisible by 2 (odd) and divisible by 2 (even).