
Question: Which images look similar and which ones look different?
Answer: Images A, C, and D look similar, even though they have different sizes. Images B and E look different.
Question: Do images B and E look like the other three images?
Answer: No, images B and E do not look like the other three images (A, C, D). Image B appears elongated, and image E appears compressed and fatter.
Question: Why?
Answer: Images A, C, and D are similar because they all are rectangles. Image E is a square (width equals height), unlike the rectangular shapes of A, C, and D. Image B, although rectangular, does not look like images A, C, and D. It appears to be more elongated.
Question: Can we observe any pattern to answer this question? Perhaps by measuring the rectangles? What makes images A, C, and D appear similar, and B and E different?
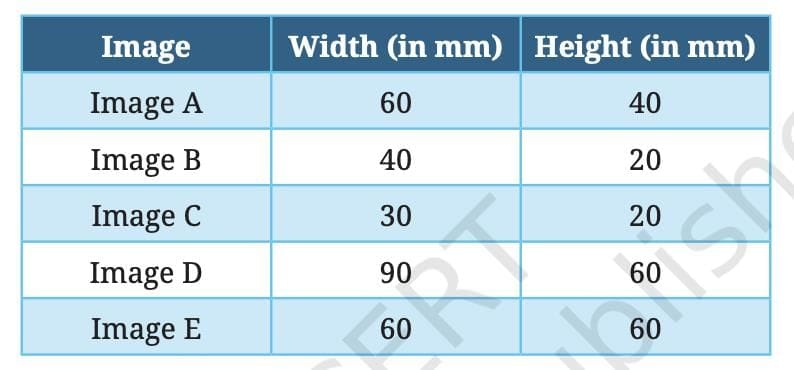
Answer:
Comparison between Image A and Image C:
- Image C is exactly half the width and half the height of Image A.
- This means both the width and height are reduced by the same factor — they are divided by 2.
- When both dimensions (width and height) are changed by the same factor using multiplication or division, the shape and look of the image remain the same.
- Therefore, even though Image C is smaller, it looks similar to Image A.
Similarly compare Image A and Image D yourself
Comparison between Image A and Image B:
- Image B is 20 millimetres less in both width and height compared to Image A.
- In this case, the change is made by subtracting a fixed amount, not by dividing or multiplying by the same number.
- Also, even though the height of B is half the height of A, the width is not half — so the change is not by the same factor.
- When the width and height do not change by the same factor, the shape of the image changes.
- That is why Image B looks different from Image A, even though both have the same difference in size.
Similarly compare Image A and Image E yourself
Question: Can you check by what factors the width and height of image D change as compared to image A? Are the factors the same?
Answer: To compare Image A (60 mm width, 40 mm height) with Image D (90 mm width, 60 mm height):
- Width factor: 90 ÷ 60 = 1.5
- Height factor: 60 ÷ 40 = 1.5
The factors are the same (1.5), confirming that the width and height of Image D change by the same factor compared to Image A, making them proportional.
Images A, C, and D look similar because their widths and heights havechanged by the same factor. We say that the changes to their widths andheights are proportional.
163
Example 4: Is the teacher-to-student ratio in your school proportional to the one in my school (5:170)?
Answer: Let’s assume:
- There are 10 teachers
- There are 340 students
Then the ratio of teachers to students in your school is: 10 : 340
Now simplify the ratio by dividing both numbers by 10:
(10 ÷ 10) : (340 ÷ 10) = 1 : 34
Final Answer: 10 : 340 or simplified: 1 : 34
You can fill in the blanks with the actual number of teachers and students in your school to calculate your own ratio.
Example 5: What is the ratio of width to height of the blackboard? Can you draw a rectangle with proportional width and height? Do classmates’ rectangles look the same?
Answer: Suppose the width of the blackboard is 240 cm and the height is 120 cm.
Step1: Find the ratio of width to height
Ratio = Width : Height
= 240 : 120
Now simplify the ratio by dividing both numbers by 120:
= (240 ÷ 120) : (120 ÷ 120)
= 2 : 1
Step2: Multiply the ratio of width to height with same number
= 2 x 2 : 1 x 1 = 4: 2
or
= 2 x 4 : 1 x 4 = 8 : 4
Step 3: Draw a rectangle in the notebook
Now, draw a rectangle in your notebook using the same ratio. For example, you can draw:
- Width = 8 cm
- Height = 4 cm (because 8 : 4 = 2 : 1)
Ask your classmates to do the same. If everyone uses the same ratio, all rectangles should look the same in shape, even if sizes are different.
Page 164
Example 7: Fill in the missing numbers for ratios proportional to 14 : 21:
(a) ? : 42
Answer:
We are told that the second term is 42.
- In the original ratio, the second term is 21.
- To get 42, we do:
21 × 2 = 42 - So, we multiply the first term also by 2:
14 × 2 = 28
Final Answer – 28 : 42
(b) 6 : ?
Answer: We are told the first term is 6.
- In the original ratio, the first term is 14.
- To get 6, we ask: what multiplied by 14 gives 6?
We rewrite this:
14 × (some number) = 6
The multiplying factor is 6/14 = 3/7
So, now multiply the second term (21) by 3/7:
- 21 × 3/7 = 9
Answer: 6 : 9
(c) 2 : ?
Answer: We are told the first term is 2.
- In the original ratio, the first term is 14.
- To get 2, we use the multiplication factor:
14 × (1/7) = 2 - So, use the same factor on 21:
21 × (1/7) = 3
Final Answer – 2 : 3
Filter Coffee!
Filter coffee is a beverage made by mixing coffeedecoction with milk. Manjunath usually mixes 15mL of coffee decoction with 35 mL of milk to makeone cup of filter coffee in his coffee shop.In this case, we can say that the ratio of coffeedecoction to milk is 15 : 35.If customers want ‘stronger’ filter coffee,Manjunath mixes 20 mL of decoction with 30 mL ofmilk. The ratio here is 20 : 30.