Patterns and Properties of Perfect Squares
Page 4
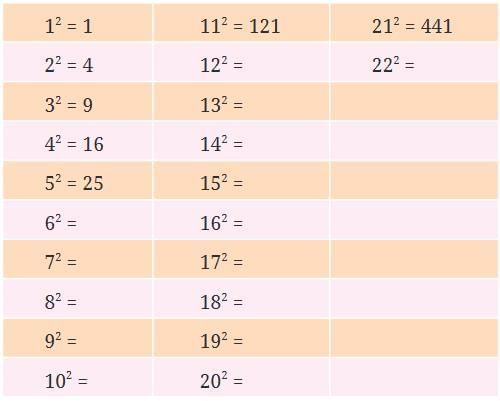
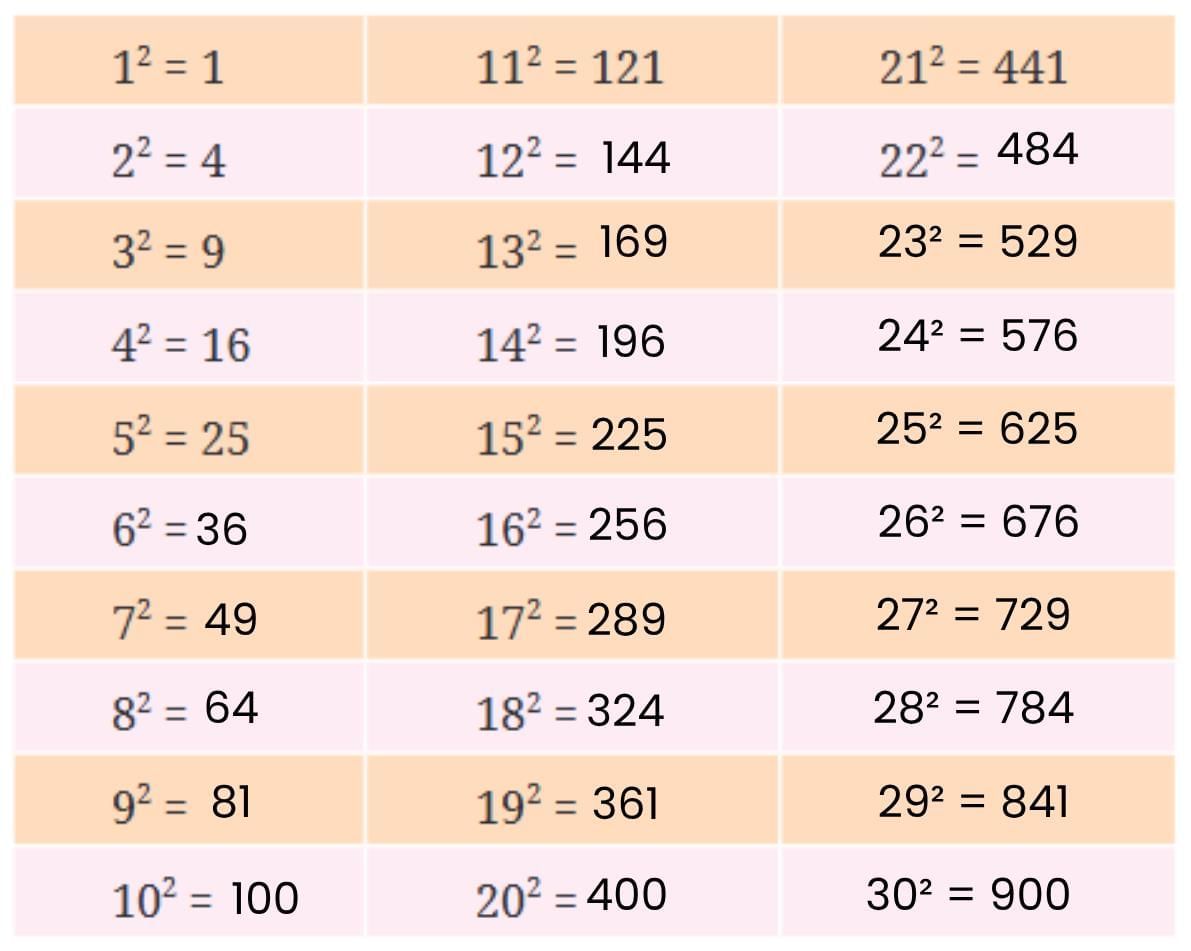
Q. Find the squares of the first 30 natural numbers and fill in the table below.
Answer:Q. What patterns do you notice? Share your observations and make conjectures.
Answer:
The squares of the first 30 natural numbers are:
- 1² = 1, 2² = 4, 3² = 9, 4² = 16, 5² = 25, 6² = 36, 7² = 49, 8² = 64, 9² = 81, 10² = 100
- 11² = 121, 12² = 144, 13² = 169, 14² = 196, 15² = 225, 16² = 256, 17² = 289, 18² = 324, 19² = 361, 20² = 400
- 21² = 441, 22² = 484, 23² = 529, 24² = 576, 25² = 625, 26² = 676, 27² = 729, 28² = 784, 29² = 841, 30² = 900
- Observation: The units digits of these square numbers are only 0, 1, 4, 5, 6, or 9. None of them end in 2, 3, 7, or 8.
Q. If a number ends in 0, 1, 4, 5, 6 or 9, is it always a square?
Answer: No. For example, the number 26 ends in 6, but it is not a perfect square. Just looking at the units digit is not enough to confirm if a number is a square, but it can tell us if a number is not a square.
Q. Write 5 numbers such that you can determine by looking at their units digit that they are not squares.
Answer: Any number ending in 2, 3, 7, or 8 is not a perfect square. Five examples are: 12, 33, 47, 58, and 102.
Page 5
Q. Which of the following numbers have the digit 6 in the units place?
(i) 38² (ii) 34² (iii) 46² (iv) 56² (v) 74² (vi) 82²
Answer:
To find the units digit (that is, the last digit) of the square of a number, we only need to look at the units digit of the original number, because squaring affects the last digit in a predictable way.
Here is a table showing what happens when we square numbers ending in each digit from 0 to 9:
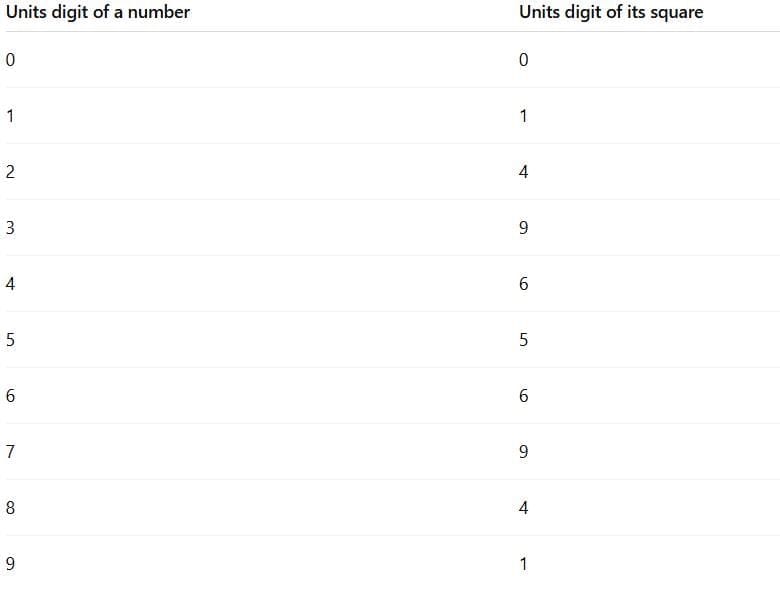
From this table, we observe that:
A number’s square ends in 6 if the number itself ends in 4 or 6.
Checking Each Option:
- 38²: The number ends in 8 → 8² ends in 4 → does not end in 6
- 34²: The number ends in 4 → 4² ends in 6 → ends in 6
- 46²: The number ends in 6 → 6² ends in 6 → ends in 6
- 56²: The number ends in 6 → 6² ends in 6 → ends in 6
- 74²: The number ends in 4 → 4² ends in 6 → ends in 6
- 82²: The number ends in 2 → 2² ends in 4 → does not end in 6
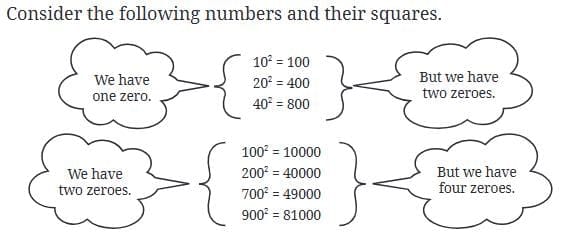
Q. If a number contains 3 zeros at the end, how many zeros will its square have at the end?
Answer: Its square will have 6 zeros at the end. The number of zeros at the end of a square is always double the number of zeros at the end of the original number.
Q. What do you notice about the number of zeros at the end of a number and the number of zeros at the end of its square? Will this always happen? Can we say that squares can only have an even number of zeros at the end?
Answer: The number of zeros at the end of a square is always double the number of zeros in the original number. This will always happen. Yes, we can say that perfect squares can only have an even number of zeros at the end.
Q. What can you say about the parity of a number and its square?
Answer: The square of an even number is always even. The square of an odd number is always odd.
Page 7
Q. Find how many numbers lie between two consecutive perfect squares. Do you notice a pattern?
Answer: Between n² and (n+1)², there are 2n non-perfect square numbers. For example, between 2² (4) and 3² (9), there are 22 = 4 numbers (5, 6, 7, 8). Between 3² (9) and 4² (16), there are 23 = 6 numbers (10, 11, 12, 13, 14, 15).
Q. How many square numbers are there between 1 and 100? How many are between 101 and 200? Using the table of squares you filled earlier, enter the values below, tabulating the number of squares in each block of 100. What is the largest square less than 1000?
Answer:
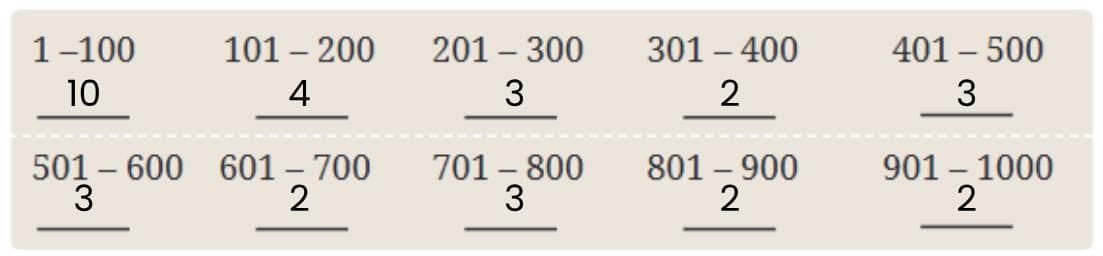
The largest square less than 1000 is 31² = 961.
Q. Can you see any relation between triangular numbers and square numbers? Extend the pattern shown and draw the next term.
Answer:The sum of two consecutive triangular numbers is a perfect square.
- 1 + 3 = 4 = 2²
- 3 + 6 = 9 = 3²
- 6 + 10 = 16 = 4²
- The next term would be

10 + 15 = 25 = 5²
Page 10: Figure it Out
1. Which of the following numbers are not perfect squares?
(i) 2032 (ii) 2048 (iii) 1027 (iv) 1089
Answer:
- (i) 2032 ends in 2. Not a perfect square.
- (ii) 2048 ends in 8. Not a perfect square.
- (iii) 1027 ends in 7. Not a perfect square.
- (iv) 1089 might be. lets find out:
We know, 30²=900, so, 1089 is very close to 900, lets list the squares of the next numbers.
312 = 961
322 = 1024
33² = 1089. So, 1089 is a perfect square. - So, (i), (ii), and (iii) are not perfect squares.
2. Which one among 64², 108², 292², 36² has last digit 4?
Answer: A square has the last digit 4 if the original number’s last digit is 2 or 8.
Therefore, 108² and 292² will have the last digit 4.
3. Given 125² = 15625, what is the value of 126²?
(i) 15625 + 126 (ii) 15625 + 262 (iii) 15625 + 253 (iv) 15625 + 251 (v) 15625 + 512
Answer: From the question we know that, 125² = 15625. That means 15625 is the sum of 125 consecutive natural numbers. To find 126², we need to find the 126th odd number and add it with 125th odd number that is 15625.
126th odd number = (2 x 126) -1 = 251.
Therefore, 1262 = 15625 + 251 = 15876.
4. Find the length of the side of a square whose area is 441 m².
Answer: The length is √441. We know 20²=400 and the number ends in 1, so the root must end in 1 or 9. Trying 21, we get 21² = 441. The length is 21 m.
5. Find the smallest square number that is divisible by each of the following numbers: 4, 9, and 10.
Answer: First, find the LCM of 4, 9, and 10.
- 4 = 2², 9 = 3², 10 = 2 × 5.
- LCM = 2² × 3² × 5 = 4 × 9 × 5 = 180.
- The prime factorization of 180 is 2 × 2 × 3 × 3 × 5. To make it a perfect square, all prime factors must be in pairs. The factor 5 is not paired.
- We must multiply by 5: 180 × 5 = 900.
- The smallest square number is 900.
6. Find the smallest number by which 9408 must be multiplied so that the product is a perfect square. Find the square root of the product.
Answer:
Prime factorization of 9408:
9408 = 2 × 4704
= 2 × 2 × 2352
= 2 × 2 × 2 × 2 × 2 × 2 × 3 × 7 × 7.
In pairs: (2×2) × (2×2) × (2×2) × (7×7) × 3.
The factor 3 is unpaired.
The smallest number to multiply by is 3.
The new number is 9408 × 3 = 28224.
The square root is 2 × 2 × 2 × 7 × 3 = 168.
7. How many numbers lie between the squares of the following numbers?
(i) 16 and 17 (ii) 99 and 100
Answer: There are 2n numbers between n² and (n+1)².
- (i) Between 16² and 17²: 2 × 16 = 32 numbers.
- (ii) Between 99² and 100²: 2 × 99 = 198 numbers.
8. In the following pattern, fill in the missing numbers:
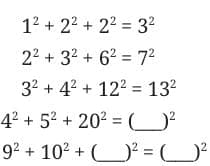
Answer: The pattern is a² + b² + (ab)² = (ab+1)².
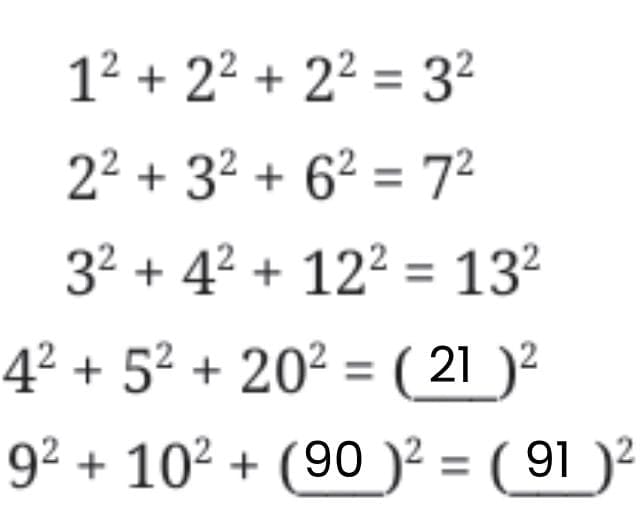
9. How many tiny squares are there in the following picture? Write the prime factorisation of the number of tiny squares.

Answer: There are 1025 tiny squares
1025 = 5 × 5 × 41
Page 12
Q. Complete the table below.
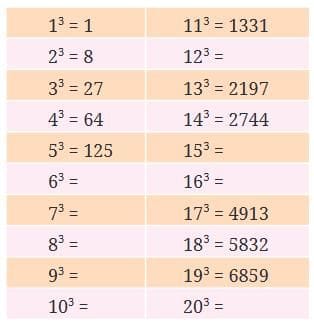
Answer:
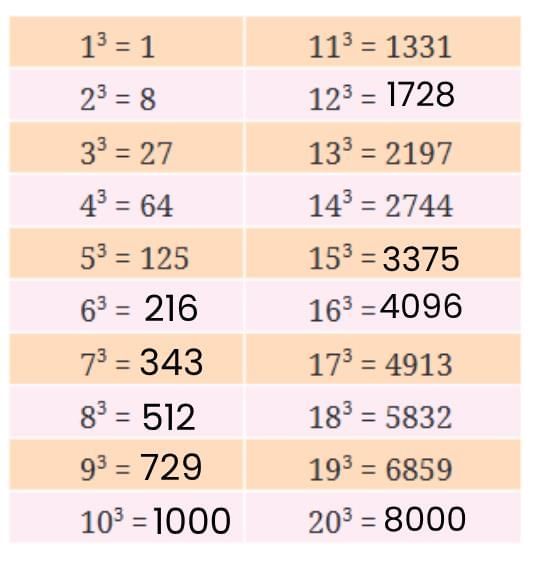
Q. What patterns do you notice in the table above?
Answer: The last digit of a cube can be any digit from 0 to 9.
- Cube of a number ending in 1 ends in 1.
- Cube of a number ending in 2 ends in 8.
- Cube of a number ending in 3 ends in 7.
- Cube of a number ending in 4 ends in 4.
- Cube of a number ending in 5 ends in 5.
- Cube of a number ending in 6 ends in 6.
- Cube of a number ending in 7 ends in 3.
- Cube of a number ending in 8 ends in 2.
- Cube of a number ending in 9 ends in 9.
- Cube of a number ending in 0 ends in 0.
Q. We know that 0, 1, 4, 5, 6, 9 are the only last digits possible for squares. What are the possible last digits of cubes?
Answer: All digits from 0 to 9 are possible last digits for cubes.
Page 13
Q. Similar to squares, can you find the number of cubes with 1 digit, 2 digits, and 3 digits? What do you observe?
Answer:
- 1-digit cubes: 1³, 2³ (1, 8) -> 2 cubes.
- 2-digit cubes: 3³, 4³ (27, 64) -> 2 cubes.
- 3-digit cubes: 5³, 6³, 7³, 8³, 9³ (125, 216, 343, 512, 729) -> 5 cubes.
- Observation: The number of cubes in a given range of digits is not as regular as squares.
Q. Can a cube end with exactly two zeroes (00)? Explain.
Answer: No. For a number to end in zero, it must be a multiple of 10. The cube of a multiple of 10 (like 10, 20, 30) will have a number of zeros that is a multiple of 3. For example, 10³ = 1000 (3 zeros), 20³ = 8000 (3 zeros). It is impossible for a perfect cube to end in exactly two zeros.
Q. The next two taxicab numbers after 1729 are 4104 and 13832. Find the two ways in which each of these can be expressed as the sum of two positive cubes.
Answer:
- 4104: 4104 = 2³ + 16³ = 8 + 4096. Also, 4104 = 9³ + 15³ = 729 + 3375.
- 13832: 13832 = 2³ + 24³ = 8 + 13824. Also, 13832 = 18³ + 20³ = 5832 + 8000.
Page 14
Q. Can you tell what this sum is without doing the calculation?
91+93 +95 + 97 + 99 + 101 + 103 + 105 + 107 + 109.
Answer: This is a series of 10 consecutive odd numbers. The sum of n consecutive odd numbers starting from the correct term gives n³. The sum shown is 10³ that is, 1000.
Page 15
Q. Find the cube roots of these numbers:
(i) ³√64 (ii) ³√512 (iii) ³√729
Answer:
(i) ³√64
Step 1: Prime factorisation
64 = 2 × 2 × 2 × 2 × 2 × 2
Step 2: Group the factors into triplets
(2 × 2 × 2) × (2 × 2 × 2)
cube root = 2 × 2 = 4
(ii) ³√512
Step 1: Prime factorisation
512 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
Step 2: Group the factors into triplets
(2 × 2 × 2) × (2 × 2 × 2) × (2 × 2 × 2)
cube root = 2 × 2 × 2 = 8
(iii) ³√729
Step 1: Prime factorisation
729 = 3 × 3 × 3 × 3 × 3 × 3
Step 2: Group the factors into triplets
(3 × 3 × 3) × (3 × 3 × 3)
cube root = 3 × 3 = 9
Page 16: Figure it Out
1. Find the cube roots of 27000 and 10648.
Answer:
(i) ³√27000
Step 1: Prime factorisation
27000 = 27 × 1000
= (3 × 3 × 3) × (2 × 2 × 2 × 5 × 5 × 5)
Step 2: Group the prime factors into triplets
(3 × 3 × 3) × (2 × 2 × 2) × (5 × 5 × 5) = (3³) × (2³) × (5³)
cube root = 3 × 2 × 5 = 30
(ii) ³√10648
Step 1: Prime factorisation
10648 = 2 × 2 × 2 × 11 × 11 × 11 = 2³ × 11³
Step 2: Group the prime factors into triplets
(2 × 2 × 2) × (11 × 11 × 11)
cube root = 2 × 11 = 22
2. What number will you multiply by 1323 to make it a cube number?
Answer: Prime factorization of 1323 = 3 × 441 = 3 × 21² = 3 × (3×7)² = 3 × 3² × 7² = 3³ × 7².
- The factor 3 is a triplet, but 7 is only a pair. We need one more 7 to make it a triplet.
- You must multiply by 7.
3. State true or false. Explain your reasoning.
(i) The cube of any odd number is even.
False.
When you cube an odd number, you multiply it by itself three times:
For example:
- 3³ = 3 × 3 × 3 = 27 (odd)
- 5³ = 5 × 5 × 5 = 125 (odd)
Rule:
- Odd × Odd = Odd
- So, Odd × Odd × Odd = Odd
Thus, the cube of an odd number is also odd, not even.
(ii) There is no perfect cube that ends with 8.
False. 2³ = 8, and any number ending in 2 will have a cube ending in 8 (e.g., 12³ = 1728).
(iii) The cube of a 2-digit number may be a 3-digit number.
False. The smallest 2-digit number is 10, and 10³ = 1000 (a 4-digit number).
All other 2-digit cubes will be larger.
(iv) The cube of a 2-digit number may have seven or more digits.
False. The largest 2-digit number is 99. 99³ = 970299 (a 6-digit number). So a 2-digit number cannot have 7 or more digits
(v) Cube numbers have an odd number of factors.
False. This is true for square numbers. For a number to have an odd number of factors, it must be a perfect square. Some cube numbers are also perfect squares (e.g., 64 = 8² = 4³), and these will have an odd number of factors. But most cubes (like 8, 27) are not perfect squares and have an even number of factors.
4. You are told that 1331 is a perfect cube. Can you guess without factorisation what its cube root is? Similarly, guess the cube roots of 4913, 12167, and 32768.
Answer:
- 1331: Ends in 1, so root ends in 1. We know 10³=1000 and 20³=8000. 1331 lies between 1000 and 8000, and between 10 and 20 only 11 is a number that ends with 1. So, the root is 11.
- 4913: Ends in 3, so root ends in 7. We know 10³=1000 and 20³=8000. 4913 lies between 1000 and 8000, and between 10 and 20 only 17 is a number that ends with 1. So, the root is 17.
- 12167: Ends in 7, so root ends in 3. We know, 20³=8000 and 30³=27000. 12167 lies between 8000 and 27000. So, cube root of 12167 lies between 20 and 30. Only 23 is a number that ends with 3. So, the root is 23.
- 32768: Ends in 8, so root ends in 2. We know, 30³=27000 and 40³=64000. 32768 lies between these numbers, so cube root of 32768 lies between 30 and 40. 32 is the only number that ends with 2. So, the root is 32.
Page 17
5. Which of the following is the greatest? Explain your reasoning.
(i) 67³ – 66³ (ii) 43³ – 42³ (iii) 67² – 66² (iv) 43² – 42²
Answer:
- We know n² – (n-1)² = 2n – 1.
- We know n³ – (n-1)³ = 3n² – 3n + 1.
- (iii) 67² – 66² = 2(67) – 1 = 133.
- (iv) 43² – 42² = 2(43) – 1 = 85.
- (i) 67³ – 66³ = 3(67)² – 3(67) + 1 = 3(4489) – 201 + 1 = 13467 – 200 = 13267.
- (ii) 43³ – 42³ = 3(43)² – 3(43) + 1 = 3(1849) – 129 + 1 = 5547 – 128 = 5419.
- Comparing the results, (i) 67³ – 66³ is the greatest.
Page 18: It’s Puzzle Time!
Look at the following numbers: 3 6 10 15 1
They are arranged such that each pair of adjacent numbers adds up to a square.
Q. Try arranging the numbers 1 to 17 (without repetition) in a row in a similar way — the sum of every adjacent pair of numbers should be a square. Can you arrange them in more than one way? If not, can you explain why?
Answer:
Step 1: What sums are allowed?
Perfect squares less than or equal to 34 (because 17 + 16 = 33) are:
4,9,16,254, 9, 16, 25
So, any two neighbours in the arrangement must add up to 4, 9, 16, or 25.
Step 2: Try to find which numbers go together
List pairs of numbers from 1 to 17 whose sum is one of those perfect squares:
Sum = 4:
- 1 + 3
Sum = 9:
- 1 + 8
- 2 + 7
- 3 + 6
- 4 + 5
Sum = 16:
- 1 + 15
- 2 + 14
- 3 + 13
- 4 + 12
- 5 + 11
- 6 + 10
- 7 + 9
- 8 + 8 → not allowed (same number twice)
Sum = 25:
- 8 + 17
- 9 + 16
- 10 + 15
- 11 + 14
- 12 + 13
This tells us which numbers can be next to each other.
Step 3: Use logic and trial to arrange
Now, we try to connect these numbers step by step. After careful trial and checking, this arrangement works:
16,9,7,2,14,11,5,4,12,13,3,6,10,15,1,8,17
Let’s check that each pair adds up to a perfect square:
- 16 + 9 = 25
- 9 + 7 = 16
- 7 + 2 = 9
- 2 + 14 = 16
- 14 + 11 = 25
- 11 + 5 = 16
- 5 + 4 = 9
- 4 + 12 = 16
- 12 + 13 = 25
- 13 + 3 = 16
- 3 + 6 = 9
- 6 + 10 = 16
- 10 + 15 = 25
- 15 + 1 = 16
- 1 + 8 = 9
- 8 + 17 = 25
All pairs are correct, and every number from 1 to 17 is used exactly once.
Final Answer:
Yes, it is possible to arrange the numbers from 1 to 17 in this way. One such arrangement is:
16,9,7,2,14,11,5,4,12,13,3,6,10,15,1,8,17
No, we cannot arrange them in more than one way.