2. Power Play – Textbook Solutions

Page 22

Which expression describes the thickness of a sheet of paper after it is folded 10 times? The initial thickness is represented by the letter-number v. 

(i) 10v (ii) 10 + v (iii) 2 × 10 × v (iv) 2¹⁰ (v) 2¹⁰v (vi) 10² v

Answer: 

The correct expression for the thickness of a sheet of paper after it is folded 10 times is (v) 2¹⁰v.

When a sheet of paper is folded, its thickness doubles with each fold. This is a form of exponential growth, not linear growth.

The process can be broken down as follows:

• Initial thickness: v
• After 1 fold: The paper has 2 layers, so the thickness is 2 × v, or 2¹v.
• After 2 folds: The paper is folded again, doubling the layers to 4. The thickness becomes 4 × v, or 2²v.
• After 3 folds: The thickness doubles again to 8 times the original, or 2³v.

Following this pattern, the thickness after ‘n’ folds is given by the formula:
Total Thickness = 2ⁿ × v

For 10 folds, you substitute n = 10 into the formula:
Total Thickness = 2¹⁰v

The other options are incorrect because they represent linear relationships, whereas the folding process is exponential. For instance, 10v would imply the thickness only increases by the original amount with each fold, rather than doubling the total current thickness

What is (– 1)⁵ ? Is it positive or negative? What about (– 1)⁵⁶? 

Answer:

• The expression (–1)⁵ equals –1, which is a negative number. When a negative number is raised to an odd exponent, the result is always negative.
  The calculation is: (–1) × (–1) × (–1) × (–1) × (–1) = –1.
• What about (–1)⁵⁶?
  The expression (–1)⁵⁶ equals +1, which is a positive number. When a negative number is raised to an even exponent, the result is always positive. This happens because the negative signs are multiplied an even number of times, causing them to cancel each other out in pairs.

Is (– 2)⁴ = 16? Verify.

Answer:

Yes, the statement (–2)⁴ = 16 is correct. To verify this, you multiply –2 by itself four times:

(–2) × (–2) × (–2) × (–2) = (4) × (–2) × (–2) = (–8) × (–2) = 16.

As with the previous example, raising the negative base (–2) to an even power (4) results in a positive number.

Figure it Out 

1. Express the following in exponential form:
(i) 6 × 6 × 6 × 6                                (ii) y × y 
(iii) b × b × b × b                             (iv) 5 × 5 × 7 × 7 × 7 
(v) 2 × 2 × a × a                              (vi) a × a × a × c × c × c × c × d

Answers:
(i) 6⁴
(ii) y² 
(iii) b⁴
(iv) 5² × 7³
(v) 2² × a²
(vi) a³ × c⁴ × d

2. Express each of the following as a product of powers of their prime factors in exponential form.
(i) 648      (ii) 405           (iii) 540                (iv) 3600

Answers:
(i) 648 = 2 × 2 × 2 × 3 × 3 × 3 × 3 = 2³ × 3⁴
(ii) 405 = 3 × 3 × 3 × 3 × 5 = 3⁴ × 5 
(iii) 540 = 2 × 2 × 3 × 3 × 3 × 5 = 2² × 3³ × 5 
(iv) 3600 = 2 × 2 × 2 × 2 × 3 × 3 × 5 × 5 = 2⁴ × 3² × 5²

3. Write the numerical value of each of the following:
(i) 2 × 10³       (ii) 7² × 2³          (iii) 3 × 4⁴         (iv) (– 3)² × (– 5)²
(v) 3² × 10⁴     (vi) (– 2)⁵ × (– 10)⁶

Answers:
(i) 2 × 10³ = 2 × 1000 = 2000 
(ii) 7² × 2³ = 49 × 8 = 392 
(iii) 3 × 4⁴ = 3 × 256 = 768 
(iv) (– 3)² × (– 5)² = 9 × 25 = 225 
(v) 3² × 10⁴ = 9 × 10000 = 90000 
(vi) (– 2)⁵ × (– 10)⁶ = – 32 × 1000000 = – 32000000

Page 24

Q. Use this observation to compute the following. (i) 2⁹ (ii) 5⁷ (iii) 4⁶

^Answer:

• (i) 2⁹
  Using the rule, this can be expressed as a product of powers. For example, since 9 = 4 + 5, we can write:
  2⁹ = 2⁴⁺⁵ = 2⁴ × 2⁵
  The final value is calculated by multiplying 2 by itself 9 times:
  2⁹ = 512
• (ii) 5⁷
  This can be expressed using the same logic. For example, since 7 = 3 + 4, we have:
  5⁷ = 5³⁺⁴ = 5³ × 5⁴
  The final value is calculated by multiplying 5 by itself 7 times:
  5⁷ = 78,125
• (iii) 4⁶
  This expression can be broken down as well. For example, since 6 = 3 + 3, we have:
  4⁶ = 4³⁺³ = 4³ × 4³
  The final value is calculated by multiplying 4 by itself 6 times:
  4⁶ = 4,096

Q. Write the following expressions as a power of a power in at least two different ways:
(i) 8⁶ (ii) 7¹⁵ (iii) 9¹⁴ (iv) 5⁸

Answers:
(i) 8⁶ = (8²)³ = (8³)² 
(ii) 7¹⁵ = (7³)⁵ = (7⁵)³
(iii) 9¹⁴ = (9²)⁷ = (9⁷)²
(iv) 5⁸ = (5²)⁴ = (5⁴)²

Page 25

Q. In the middle of a beautiful, magical pond lies a bright pink lotus. The number of lotuses doubles every day in this pond. After 30 days, the pond is completely covered with lotuses. On which day was the pond half full?

Answer: 

• The number of lotuses doubles daily.
• On day 30, the pond is fully covered.
• Since the lotuses double every day, the day before (day 29), the pond must have been half full.
• This is because doubling the lotuses from day 29 to day 30 makes the pond fully covered.
  The pond was half full on day 29.

Q. Write the number of lotuses (in exponential form) when the pond was — 

(i) fully covered (ii) half covered

Answer: 

Let’s assume we start with 1 lotus on day 1.

The number of lotuses doubles each day, so:

• On day 1: 1 lotus
• On day 2: 1 × 2 = 2 lotuses
• On day 3: 2 × 2 = 4 lotuses
• On day 4: 4 × 2 = 8 lotuses
• And so on.

This pattern shows the number of lotuses on day “n” is 2^(n-1).

For day 30 (fully covered):

• Number of lotuses = 2^(30-1) = 2²⁹.

For day 29 (half covered):

• Number of lotuses = 2^(29-1) = 2²⁸.
• (i) Fully covered (day 30): 2²⁹ lotuses
• (ii) Half covered (day 29): 2²⁸ lotuses

Q. There is another pond in which the number of lotuses triples every day. When both the ponds had no flowers, Damayanti placed a lotus in the doubling pond. After 4 days, she took all the lotuses from there and put them in the tripling pond. How many lotuses will be in the tripling pond after 4 more days?

Answer: 
In the first pond (Doubling Pond), the number of lotuses double every day, so for the first 4 days it doubles every day. 
So, after the first 4 days, the number of lotuses is 1 × 2 × 2 × 2 × 2 = 2⁴. 
In the second pond (Tripling Pond), the number of lotuses triple every day, so for the next four days, they triple every day.
So, after the next 4 days, the number of lotuses is 2⁴ × 3 × 3 × 3 × 3 = 2⁴ × 3⁴

^{Q. What if Damayanti had changed the order in which she placed the f lowers in the lakes? How many lotuses would be there?}

Answer: 

• Suppose she placed 1 lotus in the tripling pond first, for 4 days:1×3⁴
• Then moved it to the doubling pond for 4 days:3⁴×2⁴= (3 × 3 × 3 × 3) × (2 × 2 × 2 × 2)

By regrouping it, this can be expressed as:

(3 x 2) x (3 x 2) x (3 x 2) x (3 x 2) = (3 x 2)⁴ = 6⁴

Q. Use this observation to compute the value of 2⁵ × 5⁵.

Answer:
2⁵ × 5⁵ = (2 × 5)⁵ = 10⁵ = 100000

Q. Simplify  and write it in exponential form.

Answer: 

Look at the Expression:
This means:

Group the Terms:
You can pair each 10 in the numerator with a 5 in the denominator:

=105×105×105×105

Simplify Each Pair:

=2×2×2×2=2⁴

Page 27

Q. What is 2¹⁰⁰ ÷ 2²⁵ in powers of 2?

Answer: 2¹⁰⁰ ÷ 2²⁵ = 2^{(100 – 25)} = 2⁷⁵

Page 29

Q. We had required a and b to be counting numbers. Can a and b be any integers? Will the generalised forms still hold true?

Answer:
The general forms you identified, known as the laws of exponents, were initially observed for counting numbers (positive integers), but they do indeed hold true when the exponents a and b are any integers (positive, negative, or zero).

Let’s verify the two main rules you’re asking about with integer exponents.

1. Product of Powers Rule: nᵃ × nᵇ = nᵃ⁺ᵇ

nᵃ × nᵇ = nᵃ⁺ᵇ

This rule states that when you multiply powers with the same base, you add the exponents. Let’s test it with a negative exponent.

• Example: Consider 3⁵ × 3⁻².
• Using the definition of a negative exponent:
  3⁻² is the same as 1 / 3². So the expression is 3⁵ × (1/3²) = 3⁵ / 3².
  This means (3×3×3×3×3) / (3×3) = 3³ = 27.
• Using the generalized rule:
  We add the exponents: 3⁵⁺⁽⁻²⁾ = 3³ = 27.

As you can see, both methods yield the same result. The rule works perfectly with integers.

2. Power of a Power Rule: (nᵃ)ᵇ = nᵃᵇ

(nᵃ)ᵇ = nᵃᵇ

This rule states that to raise a power to another power, you multiply the exponents. Let’s test this with a negative exponent as well.

• Example: Consider (4²)⁻³.
• Using the definition of a negative exponent:
  The expression means 1 / (4²)³.
  This is 1 / (4² × 4² × 4²) = 1 / 4²⁺²⁺² = 1 / 4⁶.
• Using the generalized rule:
  We multiply the exponents: 4²ˣ⁽⁻³⁾ = 4⁻⁶.
  Since 4⁻⁶ is the same as 1 / 4⁶, the results match.

These rules hold true because of the mathematical definitions for zero and negative exponents:

• Zero Exponent: n⁰ = 1
• Negative Exponent: n⁻ᵃ = 1 / nᵃ

Q. Write equivalent forms of the following.
(i) 2^{– 4}    (ii) 10^{– 5}         (iii) (– 7)^–2          (iv) (– 5)^{– 3}        (v) 10^{– 100}

Answers:
(i) 2^{– 4} = 1/2⁴
(ii) 10^{– 5} = 1/10⁵
(iii) (– 7)^–2 = 1/(– 7)²
(iv) (– 5)^{– 3} = 1/(– 5)³
(v) 10^{– 100} = 1/10¹⁰⁰

Q. Simplify and write the answers in exponential form.
(i) 2^{– 4} × 2⁷    (ii) 3² × 3^{– 5} × 3⁶         (iii) p³ × p^–10         (iv) 2⁴ × (– 4) ^{– 2}         (v) 8^p × 8^q

Answers:
(i) 2^{– 4} × 2⁷ = 2^{(–4 + 7)} = 2³
(ii) 3² × 3^{– 5} × 3⁶ = 3^{(2 – 5 + 6)} = 3³
(iii) p³ × p^–10 = p^{(3 – 10)} = p^–7
(iv) 2⁴ × (– 4) ^{– 2} = 2⁴ × 1/(–4)² = 2⁴ × 1/16 = 16 × 1/16 = 1 = 2⁰ (or 4⁰) 
(v) 8^p × 8^q = 8^{(p + q)}

Page 30

Q. Can we say that 16384 (4⁷) is 16 (4²) times larger than 1,024 (4⁵)? 

Answer: Yes, since 4⁷ ÷ 4⁵ = 4^(7-5) = 4². 

Q. How many times larger than 4^–2 is 4²

Answer: 4² ÷ 4^-2 = 4 ^(2-(-2)) = 4⁽²⁺²⁾ = 4⁴

So, 4² is 4⁴ larger than 4^–2

Q. Use the power line for 7 to answer the following questions.

Answer: 

• 2,401 × 49 = ?
  • 2,401 is 7⁴ and 49 is 7².
  • 7⁴ × 7² = 7⁴⁺² = 7⁶
  • From the power line, 7⁶ is 117,649.
• 49³ = ?
  • 49 is 7².
  • (7²)³ = 7²ˣ³ = 7⁶
  • From the power line, 7⁶ is 117,649.
• 343 × 2,401 = ?
  • 343 is 7³ and 2,401 is 7⁴.
  • 7³ × 7⁴ = 7³⁺⁴ = 7⁷
  • From the power line, 7⁷ is 823,543.
• 16,807 / 49 = ?
  • 16,807 is 7⁵ and 49 is 7².
  • 7⁵ / 7² = 7⁵⁻² = 7³
  • From the power line, 7³ is 343.
• 7 / 343 = ?
  • 7 is 7¹ and 343 is 7³.
  • 7¹ / 7³ = 7¹⁻³ = 7⁻²
  • From the power line, 7⁻² is 1/49.
• 16,807 / 8,23,543 = ?
  • 16,807 is 7⁵ and 8,23,543 is 7⁷.
  • 7⁵ / 7⁷ = 7⁵⁻⁷ = 7⁻²
  • From the power line, 7⁻² is 1/49.
• 1,17,649 × (1 / 343) = ?
  • 1,17,649 is 7⁶ and 1/343 is 7⁻³.
  • 7⁶ × 7⁻³ = 7⁶⁻³ = 7³
  • From the power line, 7³ is 343.
• (1 / 343) × (1 / 343) = ?
  • 1/343 is 7⁻³.
  • 7⁻³ × 7⁻³ = 7⁻³⁻³ = 7⁻⁶
  • Since 7⁶ is 117,649, then 7⁻⁶ is 1/117,649.

Powers of 10

Q. Write these numbers in the same way: (i) 172, (ii) 5642, (iii) 6374.

Answer: 

(i) 172
This number can be broken down by place value: 1 hundred, 7 tens, and 2 ones.
172 = (1 × 10²) + (7 × 10¹) + (2 × 10⁰)

(ii) 5642
This number is composed of 5 thousands, 6 hundreds, 4 tens, and 2 ones.
5642 = (5 × 10³) + (6 × 10²) + (4 × 10¹) + (2 × 10⁰)

(iii) 6374
This number is composed of 6 thousands, 3 hundreds, 7 tens, and 4 ones.
6374 = (6 × 10³) + (3 × 10²) + (7 × 10¹) + (4 × 10⁰)

Page 31 

Scientific NotationQ. Write the large-number facts we read just before in this form (scientific notation).
(i) The Sun is located 30,00,00,00,00,00,00,00,00,000 m from the centre of our Milky Way galaxy. 
(ii) The number of stars in our galaxy is 1,00,00,00,00,000. 
(iii) The mass of the Earth is 59,76,00,00,00,00,00,00,00,00,00,000 kg.

Answers:
(i) 3 × 10²² m (ii) 1 × 10¹¹ stars (iii) 5.976 × 10²⁴ kg

Page 32

Q. Can you say which of the three distances is the smallest?

Answer:

• The distance between the Sun and Saturn is 14,33,50,00,00,000 m = 1.4335 × 10¹² m.

• The distance between Saturn and Uranus is 14,39,00,00,00,000 m = 1.439 × 10¹² m.

• The distance between the Sun and Earth is 1,49,60,00,00,000 m = 1.496 × 10¹¹ m.

Compare and see which one has the least power of 10.

•Sun to Saturn: 1.4335 × 10¹² m -> 12

•Saturn to Uranus: 1.439 × 10¹² m -> 12

•Sun to Earth: 1.496 × 10¹¹ m -> 11

So, the distance between Sun and Earth is the smallest.

Q. Express the following numbers in standard form.
(i) 59,853      (ii) 65,950        (iii) 34,30,000         (iv) 70,04,00,00,000

Answers:
(i) 59,853 = 5.9853 × 10⁴
(ii) 65,950 = 6.595 × 10⁴
(iii) 34,30,000 = 3.43 × 10⁶
(iv) 70,04,00,00,000 = 7.004 × 10¹⁰

Page 38

Q. Calculate and write the answer using scientific notation:
(i) How many ants are there for every human in the world? 
(ii) If a flock of starlings contains 10,000 birds, how many flocks could there be in the world?

Answer:
(i) Global human population as of 2025 is 8.2 arab/8.2 billion (8.2 × 10⁹). 
Estimated population of ants globally is 20 padma/20 quadrillion (2 × 10¹⁶). 
Number of ants per human = (2 × 10¹⁶) / (8.2 × 10⁹) = (2 / 8.2) × 10(16^-9) ≈ 0.2439 × 10⁷ = 2.439 × 10⁶ ants per human. 
(ii) The estimated global population of starlings is around 1.3 arab/1.3 billion (1.3 × 10⁹). 
If a flock contains 10,000 birds (10⁴ birds). 
Number of flocks = (1.3 × 10⁹) / 10⁴ = 1.3 × 10^(9-4) = 1.3 × 10⁵ flocks.

Page 39

(iii) If each tree had about 10⁴ leaves, find the total number of leaves on all the trees in the world.

Answer:
The estimated number of trees (2023) globally stands at 30 kharab/3 trillion (3 × 10¹²). Total number of leaves = (3 × 10¹² trees) × (10⁴ leaves/tree) = 3 × 10⁽¹²⁺⁴⁾
= 3 × 10¹⁶ leaves.

(iv) If you stacked sheets of paper on top of each other, how many would you need to reach the Moon?

Answer:
Distance to the Moon is approximately 3,84,400 km = 3.844 × 10⁸ m. 
Thickness of one sheet of paper is 0.001 cm = 1 × 10^-5 m. 
Number of sheets = (3.844 × 108 m) / (1 × 10-5 m/sheet) = 3.844 × 10^{(8 – (-5))} = 3.844 

Page 40

Q. Think of some events or phenomena whose time is of the order of 
(i) 10⁵ seconds and (ii) 10⁶ seconds. Write them in scientific notation.

Answers:
(i) 10⁵ seconds ≈ 1.16 days. Example: A short trip, like a weekend getaway. 
(ii) 10⁶ seconds ≈ 11.57 days. Example: A two-week vacation.

Page 41

A fossil of Kelenken Guillermoi, a type of terror bird, is dated to 15 million years ago ( ≈_______________ seconds).

Answer:
15 million years = 15 × 10⁶ years. 
1 year ≈ 3.1536 × 10⁷ seconds. 
15 × 10⁶ years × 3.1536 × 10⁷ seconds/year ≈ 47.304 × 10¹³ seconds 
= 4.7304 × 10¹⁴ seconds.

Page 42

Plants on land started 47 crore/470 million years ago ( ≈ _______________ seconds).

Answer:
470 million years = 470 × 10⁶ years = 4.7 × 10⁸ years. 
1 year ≈ 3.1536 × 10⁷ seconds. 4.7 × 10⁸ years × 3.1536 × 10⁷ seconds/year 
≈ 14.822 × 10¹⁵ seconds = 1.4822 × 10¹⁶ seconds.

Q. Calculate and write the answer using scientific notation:
(i) If one star is counted every second, how long would it take to count all the stars in the universe? Answer in terms of the number of seconds using scientific notation. 
(ii) If one could drink a glass of water (200 ml) every 10 seconds, how long would it take to finish the entire volume of water on Earth?

Answers:
(i) The estimated number of stars in the observable universe is 2 × 10²³. Time to count = 2 × 10²³ seconds. 
(ii) Estimated number of drops of water on Earth is 2 × 10²⁵ drops (assuming 16 drops per millilitre). 
Volume of water on Earth = (2 × 10²⁵ drops) / (16 drops/ml) = 0.125 × 10²⁵ ml = 1.25 × 10²⁴ ml. 
Volume of one glass = 200 ml. 
Number of glasses = (1.25 × 10²⁴ ml) / (200 ml/glass) = 0.00625 × 10²⁴ glasses = 6.25 × 1021 glasses. 
Time to finish = (6.25 × 10²¹ glasses) × (10 seconds/glass) = 6.25 × 10²² seconds.

Figure it Out (Page 44)

Q1. Find out the units digit in the value of 2²²⁴ ÷ 4³²? [Hint: 4 = 2²]

Answer:
2²²⁴ ÷ 4³² = 2²²⁴ ÷ (2²)³² = 2²²⁴ ÷ 2⁶⁴ = 2^(224-64) = 2¹⁶⁰. 
To find the units digit of 2¹⁶⁰, observe the pattern of units digits of powers of 2: 
2¹ = 2 
2² = 4 
2³ = 8 
2⁴ = 16 (units digit is 6) 
2⁵ = 32 (units digit is 2) 
The pattern of units digits is 2, 4, 8, 6, and it repeats every 4 powers. 
Divide the exponent 160 by 4: 160 ÷ 4 = 40 with a remainder of 0. 
A remainder of 0 means the units digit is the same as the 4th power in the cycle, which is 6. So, the units digit in the value of 2²²⁴ ÷ 4³² is 6.

Q2. There are 5 bottles in a container. Every day, a new container is brought in. How many bottles would be there after 40 days?

Answer:
Initial bottles = 5 Bottles added per day = 5 (since a new container with 5 bottles is brought in) 
Total bottles after 40 days = Initial bottles + (Bottles added per day × Number of days) Total bottles = 5 + (5 × 40) = 5 + 200 = 205 bottles.

Q3. Write the given number as the product of two or more powers in three different ways. The powers can be any integers.
(i) 64³ (ii) 192⁸ (iii) 32^–5

Answers:

(i) 64³

First, note that the base 64 can be written as 2⁶, 4³, or 8². Using the power of a power rule (nᵃ)ᵇ = nᵃᵇ, we find that 64³ = (2⁶)³ = 2¹⁸. We can now express 2¹⁸ in different ways.

• Way 1: By splitting the exponent into a sum (18 = 10 + 8):
  2¹⁰ × 2⁸
• Way 2: By changing the base to 4 (since 2² = 4):
  (2²)⁹ = 4⁹
• Way 3: By changing the base to 8 (since 2³ = 8):
  (2³)⁶ = 8⁶

(ii) 192⁸

First, find the prime factors of 192, which are 2⁶ × 3. Therefore, 192⁸ = (2⁶ × 3)⁸. Using the exponent rules, we can write this in several ways.

• Way 1: By distributing the exponent to each factor inside the parenthesis:
  (2⁶)⁸ × 3⁸ = 2⁴⁸ × 3⁸
• Way 2: By changing the base of the first term:
  (2²)²⁴ × 3⁸ = 4²⁴ × 3⁸
• Way 3: By grouping common exponents after splitting a power:
  2⁴⁰ × 2⁸ × 3⁸ = 2⁴⁰ × (2 × 3)⁸ = 2⁴⁰ × 6⁸

(iii) 32⁻⁵

First, recognize that 32 = 2⁵. Using the power of a power rule, 32⁻⁵ = (2⁵)⁻⁵ = 2⁻²⁵. This can be expressed in different forms.

• Way 1: By splitting the negative exponent into a sum (-25 = -10 + -15):
  2⁻¹⁰ × 2⁻¹⁵
• Way 2: By splitting the exponent into a sum of a negative and a positive integer (-25 = -30 + 5):
  2⁻³⁰ × 2⁵
• Way 3: By rearranging the exponents using the power of a power rule:
  (2⁻⁵)⁵ = (1/32)⁵

Q4. Examine each statement below and find out if it is ‘Always True’, ‘Only Sometimes True’, or ‘Never True’. Explain your reasoning.
(i) Cube numbers are also square numbers. 
(ii) Fourth powers are also square numbers.
(iii) The fifth power of a number is divisible by the cube of that number. 
(iv) The product of two cube numbers is a cube number. 
(v) q46 is both a 4th power and a 6th power (q is a prime number).

Answers: 
(i) Cube numbers are also square numbers.

Only Sometimes True

Reasoning: A number n³ is a cube number. For it to also be a square number, it must be possible to write it as m² for some integer m.

• When it is true: Consider the cube number 64. 64 = 4³, and it is also a square number because 64 = 8². This works because the base number (4) is itself a perfect square (2²). If we take any base that is a square number, say k², its cube will be (k²)³ = k⁶. This can be rewritten as (k³)², which is a perfect square.
• When it is false: Consider the cube number 8. 8 = 2³, but 8 is not a perfect square. Similarly, 27 = 3³ is not a perfect square. This happens whenever the base is not a perfect square.

Since the statement is true for some numbers (like 1, 64, 729) but false for others (like 8, 27, 125), it is only sometimes true.

(ii) Fourth powers are also square numbers.

Always True

Reasoning: A fourth power of a number n is n⁴. Using the laws of exponents, we can rewrite this expression:
n⁴ = n²⁺² = n² × n² = (n²)²
Since n² is an integer (if n is an integer), (n²)² is the square of an integer. Therefore, any fourth power is also a perfect square.

• Example: 3⁴ = 81, which is 9² (and 9 = 3²).
• Example: 5⁴ = 625, which is 25² (and 25 = 5²).

(iii) The fifth power of a number is divisible by the cube of that number.

Always True

Reasoning: Let the number be n. Its fifth power is n⁵ and its cube is n³. To check for divisibility, we divide n⁵ by n³. Using the quotient rule for exponents (nᵃ / nᵇ = nᵃ⁻ᵇ):
n⁵ / n³ = n⁵⁻³ = n²
For any non-zero integer n, the result n² is also an integer. Since the division results in an integer, n⁵ is always divisible by n³.

(iv) The product of two cube numbers is a cube number.

Always True

Reasoning: Let the two cube numbers be a³ and b³. Their product is a³ × b³. Using the laws of exponents, we can combine this into a single term:
a³ × b³ = (a × b)³
Since a and b are integers, their product (a × b) is also an integer. Therefore, (a × b)³ is, by definition, a cube number.

Example: 8 × 27 = 2³ × 3³ = (2 × 3)³ = 6³ = 216.

(v) q⁴⁶ is both a 4th power and a 6th power (q is a prime number).

Never True

Reasoning: For an expression xᵃ to be a perfect bth power, the exponent a must be a multiple of b.

Is it a 4th power? For q⁴⁶ to be a 4th power, 46 must be divisible by 4. Since 46 ÷ 4 = 11.5, which is not an integer, q⁴⁶ is not a 4th power.

Is it a 6th power? For q⁴⁶ to be a 6th power, 46 must be divisible by 6. Since 46 ÷ 6 ≈ 7.67, which is not an integer, q⁴⁶ is not a 6th power.

Since q⁴⁶ is neither a 4th power nor a 6th power, it can’t possibly be both. Therefore, the statement is never true.

5. Simplify and write these in the exponential form.

Answer: 

• (i) 10⁻² × 10⁻⁵
  When multiplying powers with the same base, you add the exponents (nᵃ × nᵇ = nᵃ⁺ᵇ).
  10⁻² × 10⁻⁵ = 10⁻²⁺⁽⁻⁵⁾ = 10⁻⁷
• (ii) 5⁷ ÷ 5⁴
  When dividing powers with the same base, you subtract the exponents (nᵃ ÷ nᵇ = nᵃ⁻ᵇ).
  5⁷ ÷ 5⁴ = 5⁷⁻⁴ = 5³
• (iii) 9⁻⁷ ÷ 9⁴
  Using the same division rule as above:
  9⁻⁷ ÷ 9⁴ = 9⁻⁷⁻⁴ = 9⁻¹¹
• (iv) (13⁻²)⁻³
  To raise a power to another power, you multiply the exponents ((nᵃ)ᵇ = nᵃᵇ).
  (13⁻²)⁻³ = 13⁽⁻²⁾ˣ⁽⁻³⁾ = 13⁶
• (v) (m⁵n¹²)/(mn)⁹
  Assuming the expression is a fraction, first distribute the exponent in the denominator, and then apply the division rule for each base.
  1. Distribute the exponent: (m⁵n¹²)/(m⁹n⁹)
  2. Subtract exponents for each base: m⁵⁻⁹ n¹²⁻⁹
  3. Simplify: m⁻⁴n³

6. If 12² = 144 what is (i) (1.2)² (ii) (0.12)² (iii) (0.012)² (iv) 120²

Answer: 

• (i) (1.2)²
  This can be written as (12 × 10⁻¹)² = 12² × (10⁻¹)² = 144 × 10⁻² = 1.44
• (ii) (0.12)²
  This is (12 × 10⁻²)² = 12² × (10⁻²)² = 144 × 10⁻⁴ = 0.0144
• (iii) (0.012)²
  This is (12 × 10⁻³)² = 12² × (10⁻³)² = 144 × 10⁻⁶ = 0.000144
• (iv) 120²
  This can be written as (12 × 10¹)² = 12² × (10¹)² = 144 × 10² = 14,400

Figure it Out (Page 45)

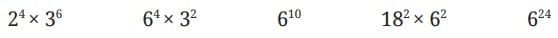
7. Circle the numbers that are the same—

Answer: 

Explanation: 

Here is the simplification of each expression:

1. 2⁴ × 3⁶
   This expression is already in its simplest prime factor form.
2. 6⁴ × 3²
   First, express 6 as its prime factors (2 × 3).
   = (2 × 3)⁴ × 3²
   = (2⁴ × 3⁴) × 3²
   = 2⁴ × 3⁽⁴⁺²⁾
   = 2⁴ × 3⁶
3. 6¹⁰
   Express 6 as its prime factors (2 × 3).
   = (2 × 3)¹⁰
   = 2¹⁰ × 3¹⁰
4. 18² × 6²
   Express 18 (2 × 3²) and 6 (2 × 3) as their prime factors.
   = (2 × 3²)² × (2 × 3)²
   = (2² × 3⁴) × (2² × 3²)
   = 2⁽²⁺²⁾ × 3⁽⁴⁺²⁾
   = 2⁴ × 3⁶
5. 6²⁴
   Express 6 as its prime factors (2 × 3).
   = (2 × 3)²⁴
   = 2²⁴ × 3²⁴

Q. 8. Identify the greater number in each of the following— (i) 4³ or 3⁴ (ii) 2⁸ or 8² (iii) 100² or 2¹⁰⁰
Answer:
(i) To compare 4³ and 3⁴, we calculate their values.
4³ = 4 × 4 × 4 = 64.
3⁴ = 3 × 3 × 3 × 3 = 81.
Since 81 is greater than 64, 3⁴ is the greater number.

(ii) To compare 2⁸ and 8², we calculate their values.
2⁸ = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 256.
8² = 8 × 8 = 64.
Since 256 is greater than 64, 2⁸ is the greater number.

(iii) To compare 100² and 2¹⁰⁰, we can evaluate or estimate their values.
100² = 100 × 100 = 10,000.
2¹⁰⁰ can be written as (2¹⁰)¹⁰. Since 2¹⁰ = 1024, 2¹⁰⁰ = (1024)¹⁰.
Clearly, (1024)¹⁰ is a vastly larger number than 10,000. Therefore, 2¹⁰⁰ is the greater number.

Q. 9. A dairy plans to produce 8.5 billion packets of milk in a year. They want a unique ID (identifier) code for each packet. If they choose to use the digits 0–9, how many digits should the code consist of?
Answer:
The code should consist of 10 digits.
The dairy needs to generate unique codes for 8.5 billion (8.5 × 10⁹) packets. Using the digits 0–9 provides 10 options for each position in the code. A code with ‘n’ digits can generate 10ⁿ unique combinations. We need to find the smallest integer ‘n’ where 10ⁿ is greater than or equal to 8.5 × 10⁹.

• If n = 9, 10⁹ = 1 billion, which is not enough codes.
• If n = 10, 10¹⁰ = 10 billion, which is more than 8.5 billion and can therefore provide a unique code for each packet.

Q. 10. 64 is a square number (8²) and a cube number (4³). Are there other numbers that are both squares and cubes? Is there a way to describe such numbers in general?
Answer:
Yes, there are other numbers that are both perfect squares and perfect cubes. Such numbers can be described in general as perfect sixth powers.
A number that is a square has prime factors with even exponents, and a number that is a cube has prime factors with exponents that are multiples of three. For a number to be both, its prime factors’ exponents must be multiples of both 2 and 3, which means they must be multiples of 6.
Therefore, any number of the form n⁶, where ‘n’ is an integer, will be both a square and a cube.

• 1 (since 1⁶ = 1, which is 1² and 1³)
• 64 (since 2⁶ = 64, which is 8² and 4³)
• 729 (since 3⁶ = 729, which is 27² and 9³)

Q. 11. A digital locker has an alphanumeric (it can have both digits and letters) passcode of length 5. Some example codes are G89P0, 38098, BRJKW, and 003AZ. How many such codes are possible?
Answer:
There are 60,466,176 possible codes.
This is calculated based on the following assumptions:

• The code has a fixed length of 5 characters.
• “Alphanumeric” includes the 10 digits (0–9) and the 26 uppercase letters of the English alphabet (A–Z), as shown in the examples. This gives a total of 36 possible characters for each position.
• Each position in the code is independent.

The total number of combinations is found by raising the number of character choices to the power of the code length:
Total codes = 36 × 36 × 36 × 36 × 36 = 36⁵ = 60,466,176.

Q. 12. The worldwide population of sheep (2024) is about 10⁹, and that of goats is also about the same. What is the total population of sheep and goats? (i) 2⁰⁹ (ii) 10¹¹ (iii) 10¹⁰ (iv) 10¹⁸ (v) 2 × 10⁹ (vi) 10⁹ + 10⁹
Answer:
The correct expressions for the total population are (v) 2 × 10⁹ and (vi) 10⁹ + 10⁹.
The calculation is:
Total Population = (Sheep Population) + (Goat Population)
Total Population = 10⁹ + 10⁹
This sum can be simplified as 2 × (10⁹). Both expressions represent the same value, which is 2 billion.

Q. 13. Calculate and write the answer in scientific notation:
Answer:

(i) If each person in the world had 30 pieces of clothing, find the total number of pieces of clothing.
Total clothing = (8 × 10⁹ people) × 30 pieces/person = 240 × 10⁹ = 2.4 × 10¹¹ pieces of clothing.

(ii) There are about 100 million bee colonies in the world. Find the number of honeybees if each colony has about 50,000 bees.
Total honeybees = (100 × 10⁶ colonies) × (50,000 bees/colony) = (1 × 10⁸) × (5 × 10⁴) = 5 × 10¹² honeybees.

(iii) The human body has about 38 trillion bacterial cells. Find the bacterial population residing in all humans in the world.
Total bacteria = (38 × 10¹² cells/person) × (8 × 10⁹ people) = (3.8 × 10¹³) × (8 × 10⁹) = 30.4 × 10²² = 3.04 × 10²³ bacterial cells.

(iv) Total time spent eating in a lifetime in seconds.
(Note: This assumes an average lifespan of 75 years and 1.5 hours spent eating per day.)
Total seconds = (75 years) × (365 days/year) × (1.5 hours/day) × (3600 seconds/hour) ≈ 148,000,000 seconds = 1.48 × 10⁸ seconds.

Q. 14. What was the date 1 arab/1 billion seconds ago?
Answer:
Assuming the current date is August 11, 2025, the date 1 billion (10⁹) seconds ago was December 4, 1993.
Here is the calculation:

• 1 billion seconds is equal to approximately 11,574 days (1,000,000,000 ÷ 86,400 seconds/day).
• Going back 11,574 days from August 11, 2025, lands on December 4, 1993. This calculation accounts for the exact number of days in each month and includes all leap years in the period (1996, 2000, 2004, 2008, 2012, 2016, 2020, and 2024).