Page 122
Figure it Out
Q1. The sum of four consecutive numbers is 34. What are these numbers?
Ans: Let four consecutive numbers be x, (x + 1), (x + 2) and (x + 3).
x + (x + 1) + (x + 2) + (x + 3) = 34
x + x + 1 + x + 2 + x + 3 = 34
4x + 6 = 34
4x = 34 – 6
4x = 28
x = 28/7 = 7.
So, (x + 1 ) = 7 + 1 = 8
(x + 2) = 7 + 2 = 9
(x + 3) = 7 + 3 = 10
Therefore, the given four consecutive numbers are 7, 8, 9, and 10.
Q2. Suppose p is the greatest of five consecutive numbers. Describe the other four numbers in terms of p.
Ans: If p is the greatest of five consecutive numbers, then the other four numbers are (p – 1), (p – 2), (p – 3), and (p – 4).
Q3. For each statement below, determine whether it is always true, sometimes true, or never true. Explain your answer. Mention examples and non-examples as appropriate. Justify your claim using algebra.
(i) The sum of two even numbers is a multiple of 3.
Ans: Let the two even numbers be 2a + 2b
Sum = 2a + 2b = 2(a + b)
For 2(a + b) to be a multiple of 3, (a + b) must be multiple of 3.
Example:
2 + 4 = 6 → divisible by 3
2 + 8 = 10 → not divisible by 3
Conclusion: Sometimes true.
(ii) If a number is not divisible by 18, then it is also not divisible by 9.
Ans: If a number is divisible by 18, then it is also divisible by 9 because 9 is a factor of 18.
18a ÷ 9 = 2a → divisible by 9.
But if a number is divisible by 9, it is not always divisible by 18.
9b ÷ 18 = b/2 → not divisible by 9.
Example: 9 is divisible by 9 but not divisible by 18.
27 is divisible by 9 but not 18.
Conclusion: Sometimes true.
(iii) If two numbers are not divisible by 6, then their sum is not divisible by 6.
Ans: Let the two numbers be a and b.
Not divisible by 6 means they do not satisfy 6∣a or 6∣b.
But their sum can still be divisible by 6.
Example: 2 and 4 → both not divisible by 6.
But, 2 + 4 = 6 → divisible by 6.
Conclusion: Sometimes true.
(iv) The sum of a multiple of 6 and a multiple of 9 is a multiple of 3.
Ans: Let the multiple of 6 be 6a, the multiple of 9 be 9b.
Sum: 6a + 9b = 3(2a + 3b)→ clearly divisible by 3.
Example:
6 + 9 = 15 → divisible by 3.
12 + 18 = 30 → divisible by 3.
Conclusion: Always true.
(v) The sum of a multiple of 6 and a multiple of 3 is a multiple of 9.
Ans: Let multiple of 6 be 6a, multiple of 3 be 3b.
Sum: 6a + 3b = 3(2a + b).
For it to be divisible by 9, 2a + b must be divisible by 3.
Example:
6 (6 × 1) + 3 (3 × 1) = 9 →divisible by 9
6 + 6 = 12 → not divisible by 9
Conclusion: Sometimes true.
Q4. Find a few numbers that leave a remainder of 2 when divided by 3 and a remainder of 2 when divided by 4. Write an algebraic expression to describe all such numbers.
Ans: L.C.M of 3 and 4 = 12.
All such numbers are given by the expression = 12a + 2.
Examples:
(i) 12 × 1 + 2 = 12 + 2 = 14.
(ii) 12 × 2 + 2 = 24 + 2 = 26.
(iii) 12 × 3 + 2 = 36 + 2 = 38.

Q5. “I hold some pebbles, not too many, When I group them in 3’s, one stays with me. Try pairing them up — it simply won’t do, A stubborn odd pebble remains in my view. Group them by 5, yet one’s still around, But grouping by seven, perfection is found. More than one hundred would be far too bold, Can you tell me the number of pebbles I hold?”
Ans: Grouped in 3’s leaves 1.
Pairing (2’s) leaves 1.
Grouped by 5 leaves 1.
Grouped by 7 is perfect.
Number ≤ 100.
L.C.M of 2, 3, and 5 = 30.
In all those cases, when we group them, 1 pebble remains.
So, the actual number of pebbles must be = 30 + 1 = 31, but 31 is not divisible by 7.
The next multiple of 30 is 2 × 30 = 60.
So, 60 + 1 = 61, but this is also not divisible by 7.
Similarly, the next number is 90 + 1 = 91.
And 91 is divisible by 7.
Hence, the number of pebbles I hold = 91.
Q6. Tathagat has written several numbers that leave a remainder of 2 when divided by 6. He claims, “If you add any three such numbers, the sum will always be a multiple of 6.” Is Tathagat’s claim true?
Ans: A number that leaves remainder of 2 when divided by 6 can be written as 6k + 2.
Three such numbers are: (6a + 2), (6b + 2), (6c + 2).
(6a + 2) + (6b + 2) + (6c + 2) = 6(a + b + c) + 6 = 6(a + b + c + 1).
This sum is divisible by 6.
So yes, Tathagat’s claim is always true.
Example: Take 20, 26, 32 → sum = 78 → divisible by 6.
Take 2, 8, 14 → sum = 24 → divisible by 6.
Page 123
Q7. When divided by 7, the number 661 leaves a remainder of 3, and 4779 leaves a remainder of 5. Without calculating, can you say what remainders the following expressions will leave when divided by 7? Show the solution both algebraically and visually.
(i) 4779 + 661 (ii) 4779 – 661
Ans: (i) 4779 + 661
= Remainder 5 + Remainder 3
= Remainder 8
8 divided by 7 → remainder 1.
(ii) 4779 – 661
= Remainder 5 – Remainder 3
= Remainder 2
Q8. Find a number that leaves a remainder of 2 when divided by 3, a remainder of 3 when divided by 4, and a remainder of 4 when divided by 5. What is the smallest such number? Can you give a simple explanation of why it is the smallest?
Ans: A number that leaves a remainder of 2 when divided by 3 is = 3x + 2
A number that leaves a remainder of 3 when divided by 4 is = 4x + 3
A number that leaves a remainder of 4 when divided by 5 is = 5x + 4
L.C.M of 3, 4, and 5 = 60
All the numbers are the same, so 4x + 3 = 3x + 2
4x – 3x = 2 – 3
x = -1
Each remainder is 1 less than the divisor.
Hence, the number is 1 less than the L.C.M = (60 – 1) = 59.
So, 59 is the smallest number that satisfies all the given conditions.
Page 126
Figure it Out
Q1. Find, without dividing, whether the following numbers are divisible by 9.
(i) 123
Ans: Digit sum of the number 123 = (1 + 2 + 3) = 6
Now, (6 ÷ 9) is not divisible by 9.
So, the whole number 123 is not divisible by 9.
(ii) 405
Ans: Digit sum of the number 405 = (4 + 0 + 5) = 9
Now, (9 ÷ 9) = 1,divisible by 9.
So, the whole number 405 is divisible by 9.
(iii) 8888
Ans: Digit sum of the number 8888 = (8 + 8 + 8 + 8) = 32
Now, (32 ÷ 9) is not divisible by 9.
So, the whole number 8888 is not divisible by 9.
(iv) 93547
Ans: Digit sum of the number 93547 = (9 + 3 + 5 + 4 + 7) = 9
Now, (28 ÷ 9) is not divisible by 9.
So, the whole number 93547 is not divisible by 9.
(v) 358095
Ans: Digit sum of the number 358095 = (3 + 5 + 8 + 0 + 9 + 5) = 30
Now, (30 ÷ 9) is not divisible by 9.
So, the whole number 358095 is not divisible by 9.
Q2. Find the smallest multiple of 9 with no odd digits.
Ans: If we multiply 9 by odd digits, we will get odd digits as a result.
So, we will multiply 9 by only even digits.
- 18 ( 1 is odd)
- 36 ( 3 is odd)
- 72 (7 is odd)
- 90 (9 is odd)
- 108 ( 1 is odd)
- 216 ( 1 is odd)
- 288(2 + 8 + 8 = 18 → divisible by 9, and digits 2,8,8 are even)
Q3. Find the multiple of 9 that is closest to the number 6000.
Ans: First Divide 6000 by 9 → (6000 ÷ 9) →Quotient = 666 and Remainder = 6
So, 5994 is 6 less than 6000.
And next closest number is 667×9 = 6003, 6003 is 3 greater than 6000.
Hence, the closest to the number 6000 that is multiple of 9 = 6003.
Q4. How many multiples of 9 are there between the numbers 4300 and 4400?
Ans: First divide 4300 by 9 = (4300 ÷ 9) = Quotient = 477 and Remainder = 7
The smallest number is 478×9 = 302 which divisible by 9. (Between 4300 – 4400)
Now, divide 4400 by 9 = (4400 ÷ 9) = Quotient = 488 and Remainder = 8
And the largest number is 488×9 = 4392 which divisible by 9. (Between 4300 – 4400)
Therefore the multiple of 9 between the number 4300 to 4400 is = (488 – 478) + 1 = 10 + 1 = 11.
Page 131
Figure it Out
Q1. The digital root of an 8-digit number is 5. What will be the digital root of 10 more than that number?
Ans: Let be the 8-digit number is = x
So, digital root of x = 5
Now the number 10 more than that is = (x + 10)
∴ Digital root of (x + 10) is = 5 + 1 + 0 = 6
Therefore 6 will be the digital root of 10 more than that number.
Q2. Write any number. Generate a sequence of numbers by repeatedly adding 11. What would be the digital roots of this sequence of numbers? Share your observations.
Ans: Let the first number of the sequence be 4.
Digital roots:
- 4 → 4
- 15 → 1 + 5 = 6
- 26 → 2 + 6 = 8
- 37 → 3 + 7 = 10 → 1 + 0 = 1
- 48 → 4 + 8 = 12 → 1 + 2 = 3
- 59 → 5 + 9 = 14 → 1 + 4 = 5
- 70 → 7 + 0 = 7
- 81 → 8 + 1 = 9
- 92 → 9 + 2 = 11 → 1 + 1 = 2
- 103 → 1 + 0 + 3 = 4
- 114 → 1 + 1 + 4 = 6
We can see that the pattern repeats every 9 terms.
Q3. What will be the digital root of the number 9a + 36b + 13?
Ans: We find the digital root by taking the expression modulo 9:
9a = 0( mod 9)
36 b = 0( mod 9)
13 = 4( mod 9)
So, 9a + 36b + 13 = 4 mod 9
Hence, the digital root is 4.
Q4. Make conjectures by examining if there are any patterns or relations between
(i) the parity of a number and its digital root.
(ii) the digital root of a number and the remainder obtained when the number is divided by 3 or 9.
Ans: (i) There is no fixed relation between Parity and digital root. Parity and digital root are independent. A number can be even or odd regardless of its digital root.
Example: Even number 14 has a digital root, 1 + 4 = 5, which is odd.
Also, even number 24 has a digital root, 2 + 4 = 6, which is even.
(ii) The digital root of a number is the same as the remainder when the number is divided by 9, except when the remainder is 0 — in that case, the digital root is 9.
If the digital root is 3, 6, or 9, then the number is divisible by 3.
Page 132-134
Figure it Out
Q1. If 31z5 is a multiple of 9, where z is a digit, what is the value of z? Explain why there are two answers to this problem.
Ans: We know that the digital root of multiples of 9 is always 9.
So, the digit root of the number 31z5 is = 9
Hence the value of z = 0 or 9.
Proceedings:
Therefore, 3 + 1 + z + 5 = 9
Or, 9 + z = 9
Or, z = 0
Now, the expression 3 + 1 + z + 5 = 9 + z must be divisible by 9.
If z = 0, then 9 + z = 9 is divisible by 9.
And when z = 9, then 9 + z = 18 is divisible by 9.
So, the value of z = 0 or 9.
And the numbers are 3105 and 3195.
That’s why there are two answers to this problem.
Q2. “I take a number that leaves a remainder of 8 when divided by 12. I take another number which is 4 short of a multiple of 12. Their sum will always be a multiple of 8”, claims Snehal. Examine his claim and justify your conclusion.
Ans: 1st number = 12k + 8
2nd number = 12k – 4
Sum = 12k + 8 + 12k – 4 = 24k + 4
According to Snehal, it is always a multiple of 8.
If we put k = 1, 24 × 1 + 4 = 24, which is a multiple of 8.
k = 2, 24 × 2 + 4 = 48, which is a multiple of 8.
k = 3, 24 × 3 + 4 = 76, which is not a multiple of 8.
So, her claim is “Sometimes True”.
Q3. When is the sum of two multiples of 3, a multiple of 6 and when is it not? Explain the different possible cases, and generalise the pattern.
Ans: Let the two numbers be 3a and 3b (multiples of 3)
Sum = 3a + 3b = 3(a + b)
This is always divisible by 3.
But it’s divisible by 6 only if the value of (a + b) is even.
So, we can conclude that
- If a + b is even -> sum divisible by 6
- If a + b is even -> sum divisible by 6
Q4. Sreelatha says, “I have a number that is divisible by 9. If I reverse its digits, it will still be divisible by 9 “.
(i) Examine if her conjecture is true for any multiple of 9.
(ii) Are any other digit shuffles possible such that the number formed is still a multiple of 9?
Ans: (i) We know that a number is divisible by 9 if the sum of its digits is divisible by 9.
So, if we reverse the digits of a number which a multiple of 9, then it will still be divisible by 9 as the sum of the digits remains the same.
Example: 117 is divisible by 9, as well as 711 and 171.
(ii) As long as the sum of digits remains the same, any shuffle will work.
Q5. If 48a23b is a multiple of 18, list all possible pairs of values for a and b.
Ans: LCM of 2 and 9 is 18.
So if the number is divisible by 2 and 9, then it is divisible by 18.
A number is divisible by 2 if the last digit is even or 0.
A number is divisible by 9 if the sum of its digits is divisible by 9.
In 48a23b, the sum of the digits apart from a and b is 4 + 8 + 2 + 3 = 17
So if a = 1 and b = 0, the number becomes 481230, which is divisible by both 2 and 9; thus divisible by 18.
No more values can be obtained.
So the values of a and b are 1 and 0, respectively.
Q6. If 3p7q8 is divisible by 44, list all possible pairs of values for p and q.
Ans: LCM of 4 and 11 is 44.
So if a number is divisible by 4 and 11, then it is divisible by 44.
If the last two digits of a number are divisible by 4, then the whole number is divisible by 4.
A number is divisible by 11 if the difference between the sum of its digits in odd places and the sum of its digits in even places is either 0 or divisible by 11.
So, (3+7+8)-(p+q) = 18-p-q must be divisible by 11 or 0.
If the values of p = 7 and q = 0, then the number becomes 37708, which is divisible by both 4 and 11; thus divisible by 44.
Also, values that are possible:
p = 5, q = 2;
p = 3, q = 4;
p = 1, q = 6;
Q7. Find three consecutive numbers such that the first number is a multiple of 2, the second number is a multiple of 3, and the third number is a multiple of 4. Are there more such numbers? How often do they occur?
Ans: The first set of numbers which satisfies the conditions is 14, 15, 16.
LCM of 2, 3, and 4 = 12
If we add 12 to the first number, then the sequence repeats.
So, the next such sets are:
14, 15, 16
26, 27, 28
38, 39, 40
50, 51, 52
And so on
Q8. Write five multiples of 36 between 45,000 and 47,000. Share your approach with the class.
Ans: Step:
Divided 45000 by 36.
We will get 1250.
Now, to get the multiple between 45000 and 47000, we have to multiply 36 by more than 1250.
So, the five multiples of 36 between 45,000 and 47,000 are:
36 × 1251 = 45036
36 × 1252 = 45072
36 × 1253 = 45108
36 × 1254 = 45144
36 × 1255 = 45180
Q9. The middle number in the sequence of 5 consecutive even numbers is 5p. Express the other four numbers in sequence in terms of p.
Ans: Let be the 5 consecutive even numbers are = x, (x + 2), (x + 4), (x + 6), (x + 8)
The middle number is (x + 4)
Therefore, (x + 4) = 5p
Or, x = 5p – 4
So, the other four numbers are =
1st number → 5p – 4
2nd number → 5p – 2
4th number → 5p + 2
5th number → 5p + 4
Q10. Write a 6-digit number that it is divisible by 15, such that when the digits are reversed, it is divisible by 6.
Ans: LCM of 3 and 5 is 15.
So if a number is divisible by both 3 and 5, then the number is divisible by 15.
A number is divisible by 3 if the sum of its digits is divisible by 3.
If the last digit of a number is 0 or 5, then the number is divisible by 5.
For the reverse number to be divisible by 6, it has to be divisible by 2 and 3.
So the first digit should be even, and the sum of the digits should be divisible by 3.
Let’s try 234105..
Here, some of the digits are 15, the last digit is 5, and in reverse order, the last digit is even.
So it satisfies all the conditions.
Q11. Deepak claims, “There are some multiples of 11 which, when doubled, are still multiples of 11. But other multiples of 11 don’t remain multiples of 11 when doubled”. Examine if his conjecture is true; explain your conclusion.
Ans: Let’s check Dipak’s hypothesis.
11 × 2 = 22
Now, the multiples of 22, such as 44, 66, 88, are all multiples of 11.
11 × 3 = 33
Now, the multiples of 33, such as 66, 99, 132, are all multiples of 11.
So, Deepak’s claim is not correct.
All doubled multiples of 11 are still multiples of 11.
Q12. Determine whether the statements below are ‘Always True’, ‘Sometimes True’, or ‘Never True’. Explain your reasoning.
(i) The product of a multiple of 6 and a multiple of 3 is a multiple of 9.
Ans: ‘Always True’
Explanation: Let be the two numbers are = 6a and 3b.
So the product of these = (6a × 3b) = 18ab
It saws that 18ab is also divisible by 9. [18 is a multiple of 9]
Example: If a = 3 and b = 2
(18 × 3 × 2) = 108, so 108 is a multipleof p.
(ii) The sum of three consecutive even numbers will be divisible by 6.
Ans: ‘Always True’
Explanation: Let be the first consecutive even number = x
So the other consecutive even numbers = (x + 2) and (2 + 4)
Therefore, sum of these number = x + x + 2 + x + 4 = 3x + 6 = 3(x + 2)
Example: If x = 6, then 3(6 + 2) = 24, divisible by 6.
When x = 10, then 3(10 + 2) = 36, divisible by 6.
(iii) If abcdef is a multiple of 6, then badcef will be a multiple of 6.
Ans: ‘Always True’
Explanation: If a number is divisible by 6 it must be divisible by 2 and 3.
Checking divisibility by 2: We check the last digits of the number, if it is even then the number must be divisible by 2.
And checking divisibility by 3: We check the sum of the digits of the number if it is divisible by 3, then the number is also divisible by 3.
Here we can see that the last digit of both the numbers ‘abcdef’ and ‘badcef’ is the same and all the digits are the same, only their positions have changed.
So, if abcdef is a multiple of 6, then badcef should be a multiple of 6.
(iv) 8 (7b-3)-4 (11b+1) is a multiple of 12.
Ans: ‘Never True’
Explanation: 8 × (7b – 3) – 4 × (11b + 1)
= 56b –24 – 44b – 4
= 12b – 28
We see that 12b is a multiple of 12 but 28 is not a multiple of 12.
So, we say that 12b – 28 is not divisible by 12.
Q13. Choose any 3 numbers. When is their sum divisible by 3? Explore all possible cases and generalise.
Ans:
- 3,6,9 → sum = 18 → Divisible by 3
- 1,2,3 → sum = 6 → Divisible by 3
- 1,2,4 → sum = 7 → Not Divisible by 3
The sum of 3 numbers is divisible by 3 if their total sum is divisible by 3
So if all numbers leave the same remainder mod 3 (like 1, 4, 7 ), or their remainders sum to 3 or 6, the result is divisible by 3.
Q14. Is the product of two consecutive integers always multiple of 2? Why? What about the product of these consecutive integers? Is it always a multiple of 6? Why or why not? What can you say about the product of 4 consecutive integers? What about the product of five consecutive integers?
Ans: Yes, the product of two consecutive integers is always a multiple of 2.
Product of two consecutive numbers: n(n + 1)
If n even → even × odd = even
If n odd → odd × even = even
No, it sometimes can be divisible by 6, if the last digits are even and the sum of the digits is divided by 3.
2 × 3 = 6 [Divisible by 6]
3 × 4 = 12 [Divisible by 6]
4 × 5 = 20 [Not divisible by 6]
The product of 4 consecutive integers is divisible by 24.
The product of 5 consecutive integers is divisible by 120.
Q15. Solve the cryptarithms —
(i) EF × E = GGG
(ii) WOW × 5 = MEOW
Ans: (i) EF × E = GGG
=10E + F × E = 100 G + 10G + G
= (10E + F) × E = 111G
If E = 1, then 10 + F = 111G
[It is not possible because for any value of F, LHS can’t be equal to RHS]
If E = 2, then (20 + F) × 2 = 111G
[It is also not possible because for any value of F, LHS can’t be equal to RHS]
For E = 3, then (30 + F) × 3 = 111G
=90 + 3F = 111G
If F = 7 and G = 1, then LHS = RHS.
∴ The values of E, F, and G are 3, 7, and 1, respectively.
(ii) WOW × 5 = MEOW
Using the same process as the previous one.
(100W + 10O + W) × 5 = MEOW
⇒ (101 W + 10 O) × 5 = MEOW
⇒ 505 W + 50 O = MEOW
Let’s try possible values of W and O such that the result is a 4-digit number.
If we set W = 5 and O = 7, we obtain a 4-digit number.
505 × 5 + 50 × 7 = 2875
On the right-hand side, if MEOW = 2875
W = 5, O = 7
1000M + 100E + 10O + W = 1000M + 100E + 70 + 5 = 1000M + 100E + 75
If we take M = 2 and E = 8, then it satisfies the LHS.
So, the values of M, E, O, and W are 2, 8, 7, and 5, respectively.
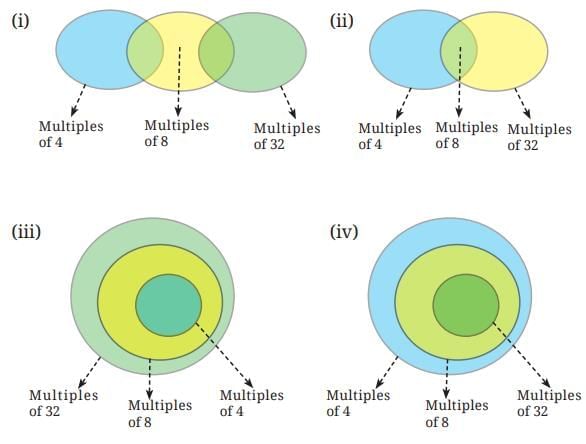
Q16. Which of the following Venn diagrams captures the relationship between the multiples of 4, 8, and 32?
Ans: The correct answer is option (iv).
Here are the reasons for the answer.
- Every multiple of 32 is also a multiple of 8 and 4.
- Every multiple of 8 is also a multiple of 4.
- But not every multiple of 4 is a multiple of 8 or 32.