Class 4th Mathematics ( Maths Mela) Solutions

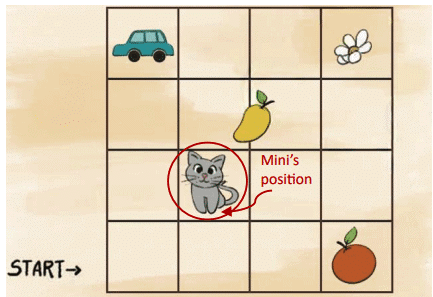
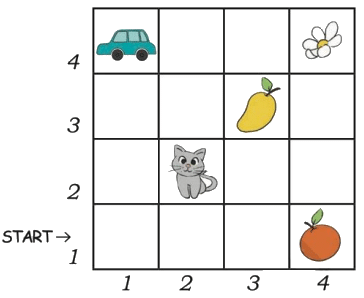
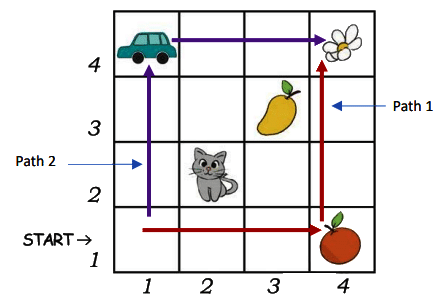
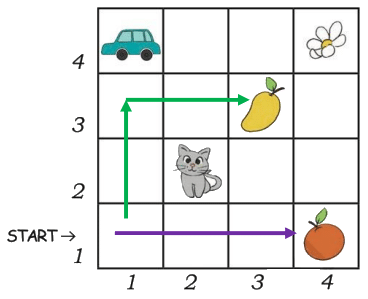
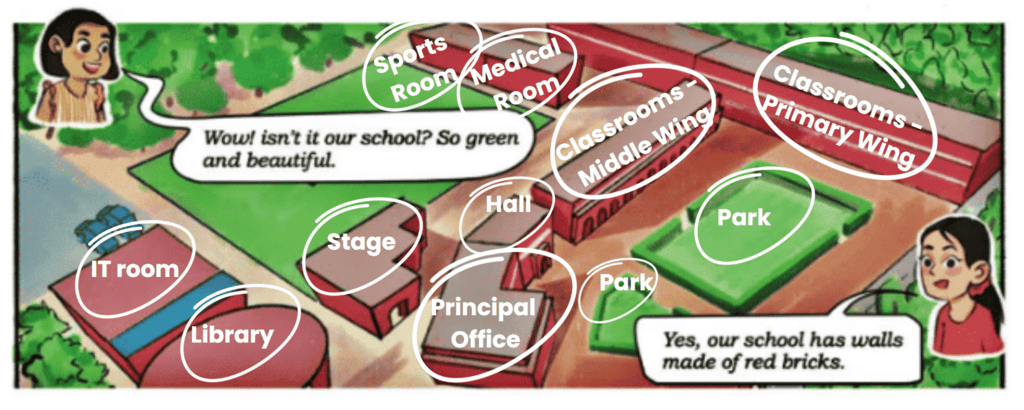
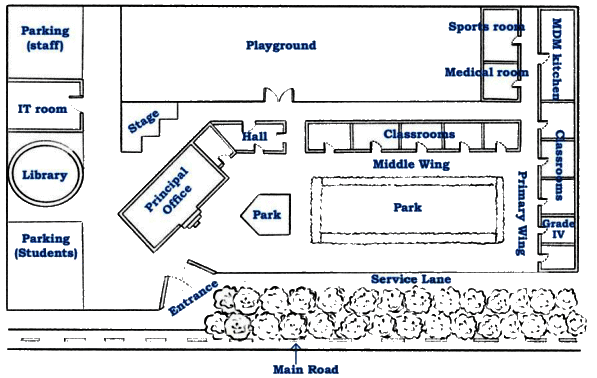
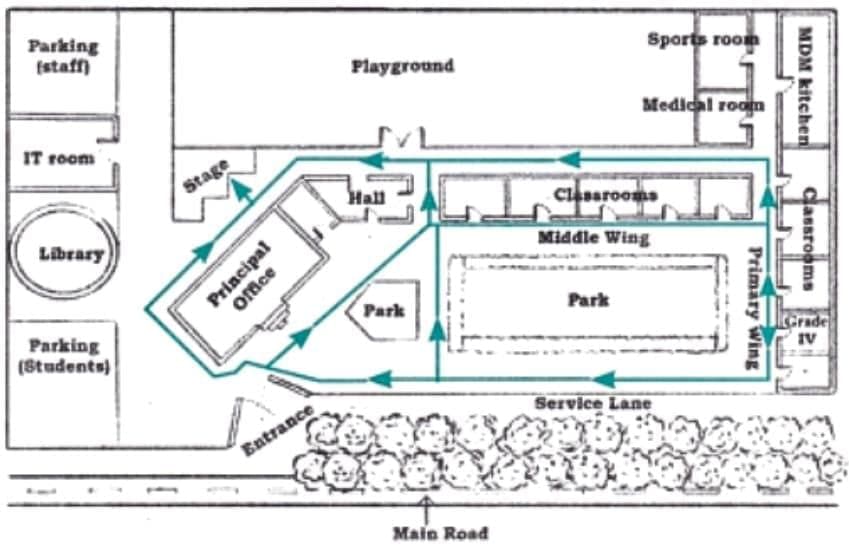
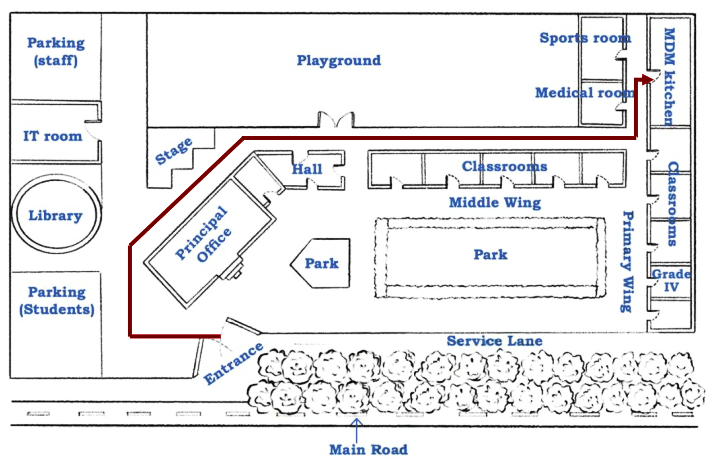
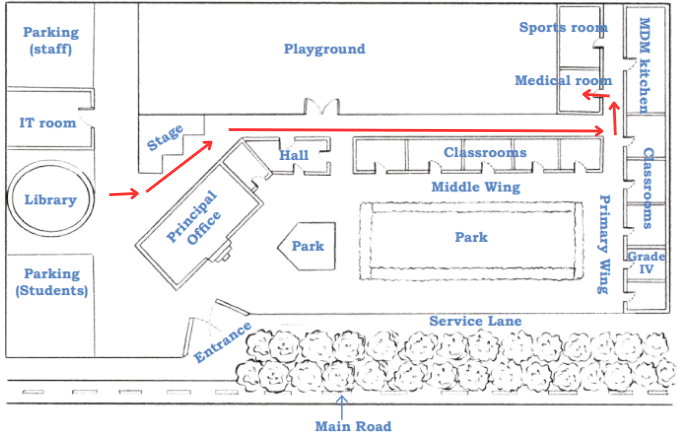
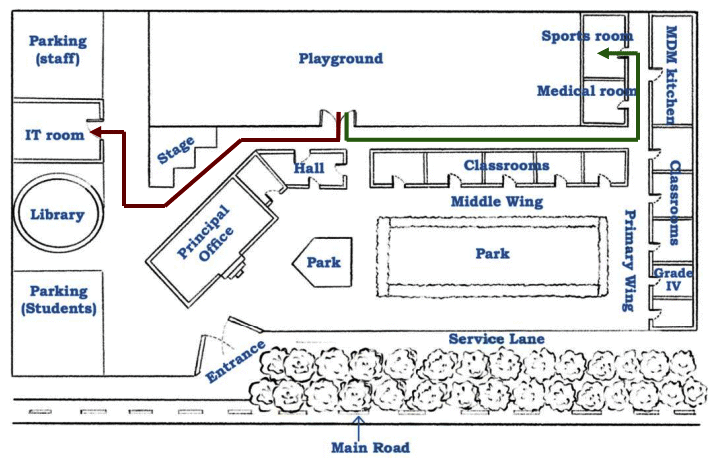
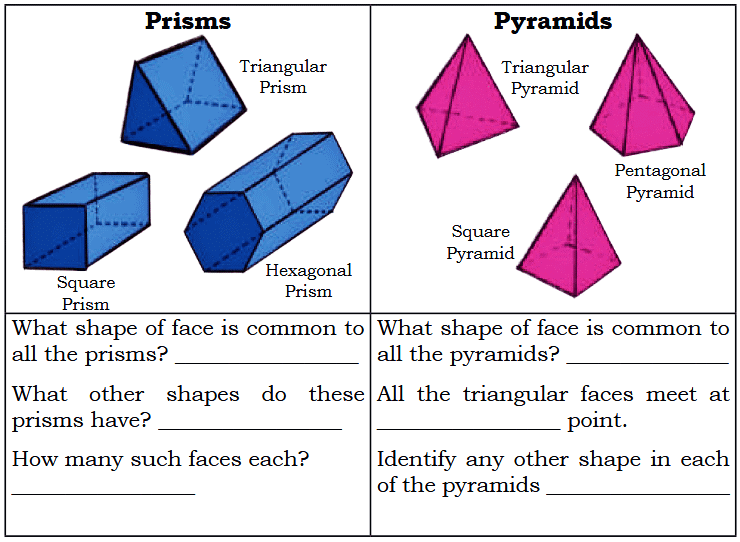
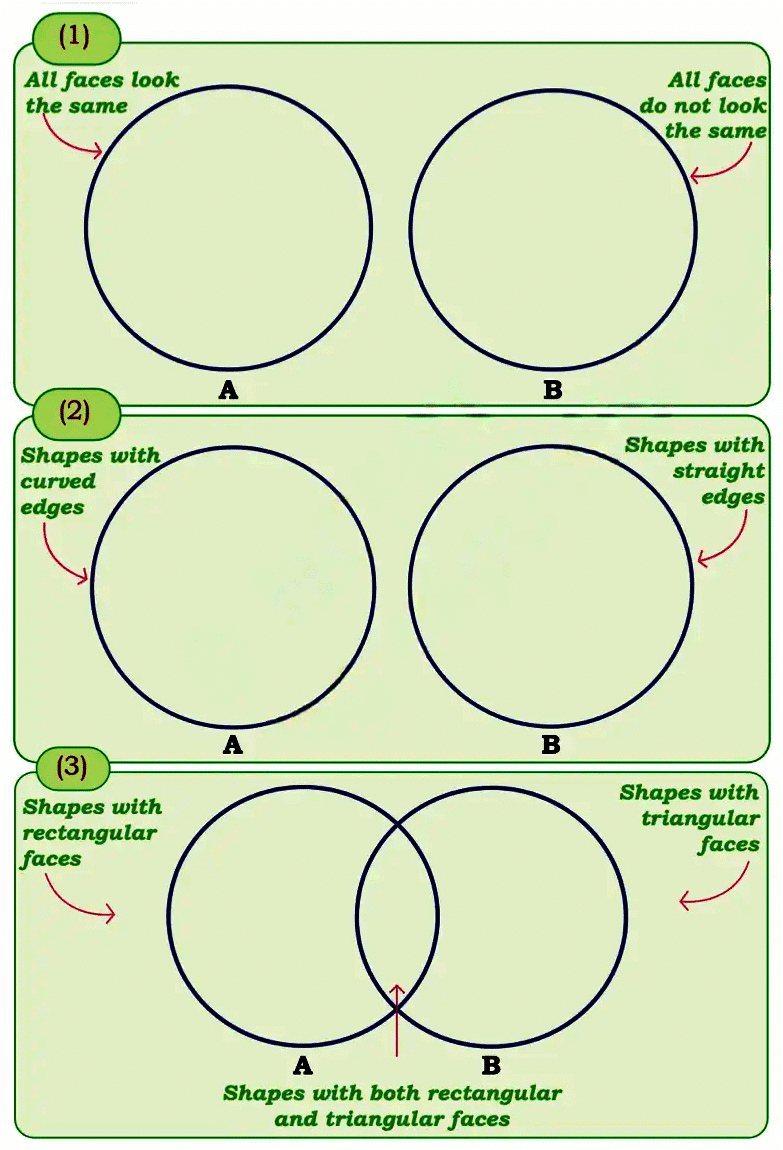
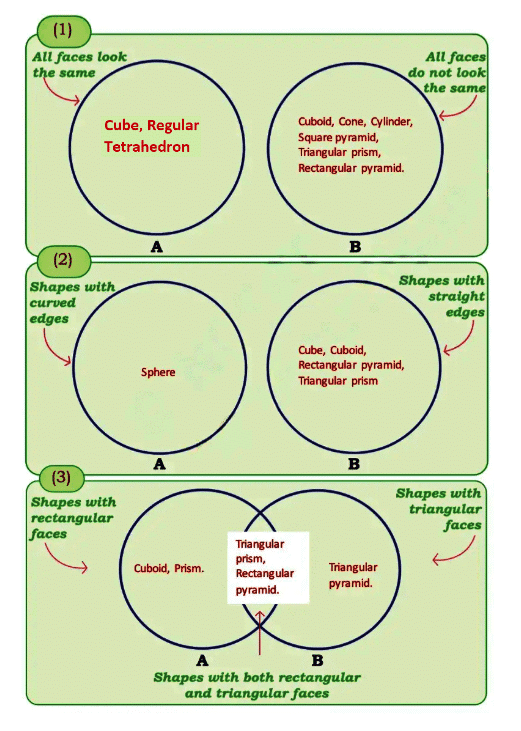
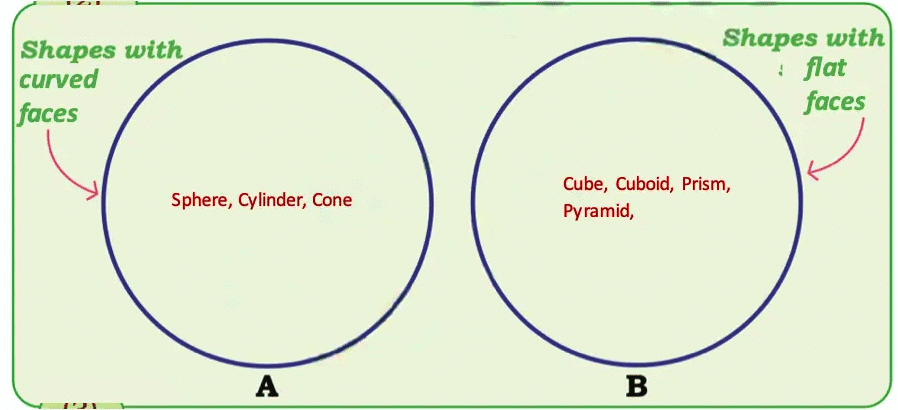
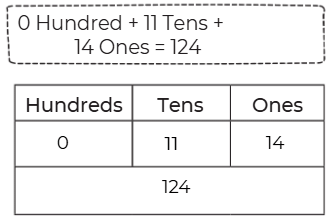
Page 39 (Let Us Do)

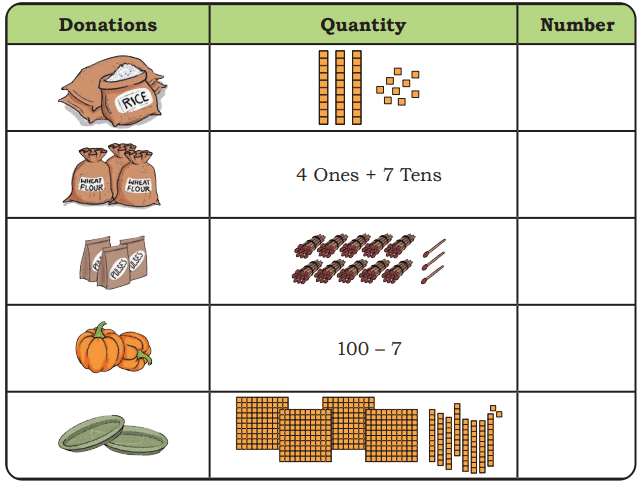
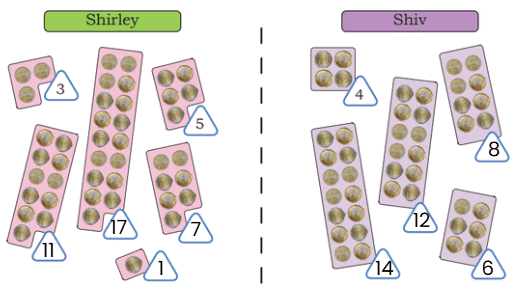
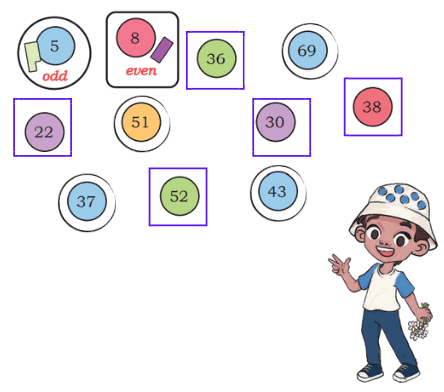
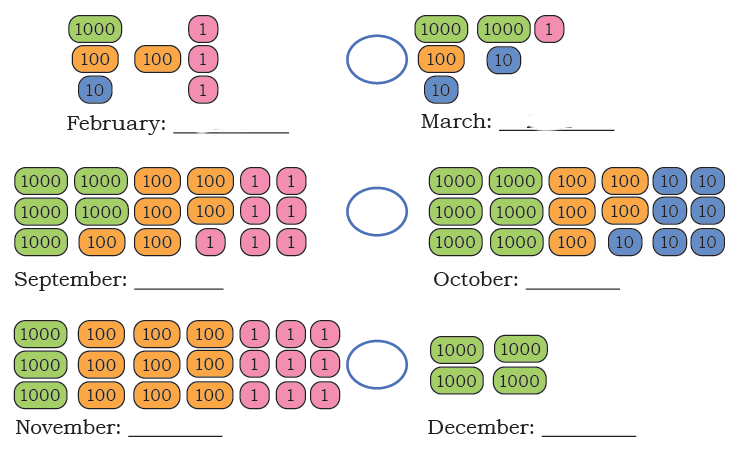
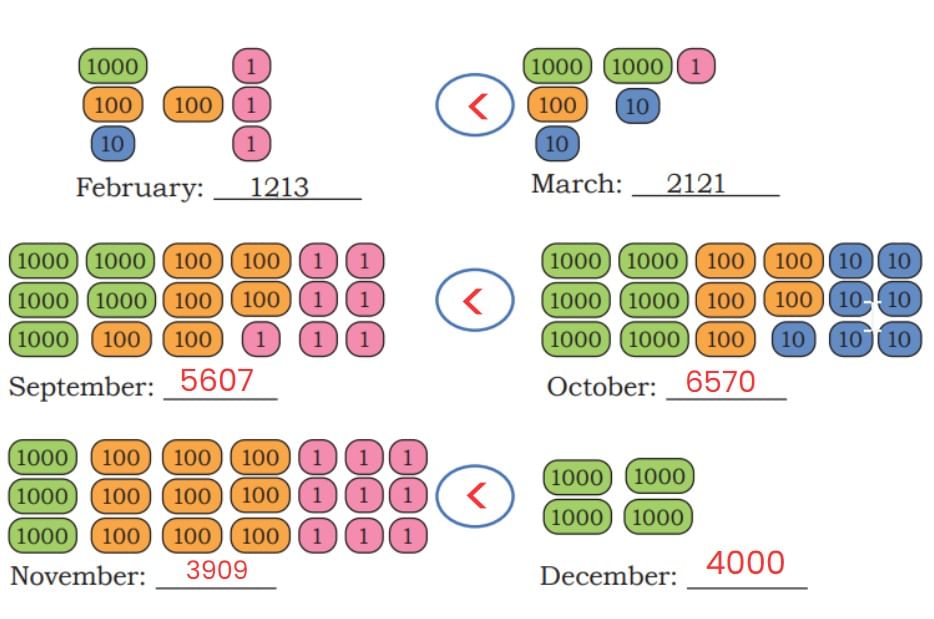
Q: Jaspreet and Gulnaz receive many donations.  The donations are shown in the table below. Write the number in each case.

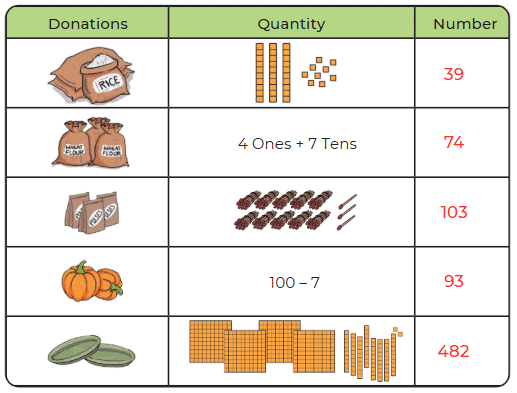
Ans:

Page 40 (Let Us Do)

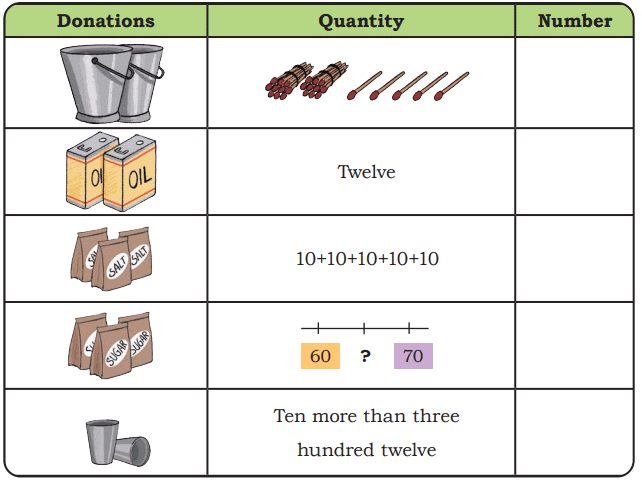
Ans: 

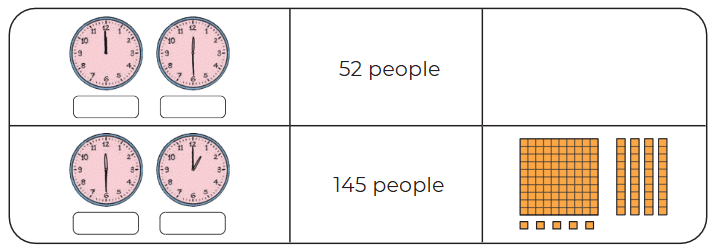
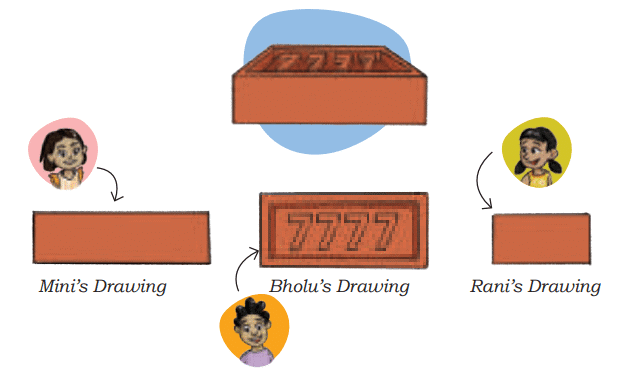
Q: Write the time and draw the number of people who had food at different time slots using HTO blocks as shown below.

The time slot when the most number of people came for lunch is _____________________.
The time slot when the least number of people came for lunch is _____________________.

Ans:

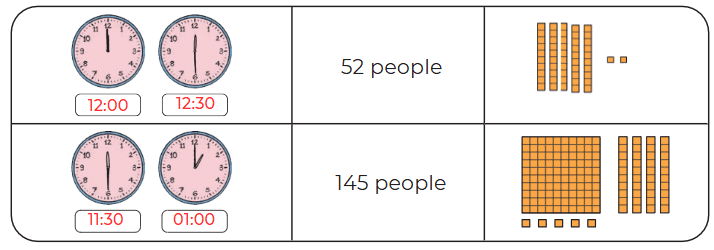
Ans: 

The time slot when the most number of people came for lunch is 1:30 to 2:00.
The time slot when the least number of people came for lunch is 12:00 to 12:30.

Let Us Do

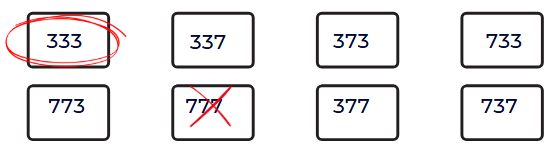
Q1:
(a) Make 3-digit numbers using the digits 3 and 7. Write the numbers in the boxes given below. Circle the smallest and cross out the largest.Ans: The possible 3-digit numbers using digits 3 and 7 (with repetition allowed) are:

• Smallest number: 333 (circle this)  
• Largest number: 777 (cross this out)

(b) Make six 3-digit numbers using the digits 3, 5, 0, 8 such that all numbers are less than 550. You can repeat the digits.Ans:
Possible 3-digit numbers less than 550 using digits 3, 5, 0, 8 with repetition:

(c) Mark the numbers you made in 1(b) on the number line.Ans: 

Page 42 (Let Us Do)

Q2: Fill in the blanks with appropriate numbers.
(a) 
Ans:

(b)
Ans:

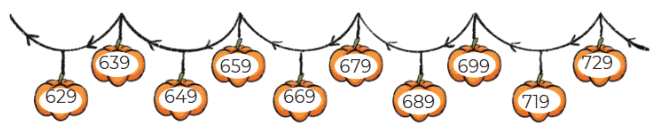
(c)
Ans:

(d) 
Ans:

(e) 
Ans: 

Page 43 (Let Us Do)

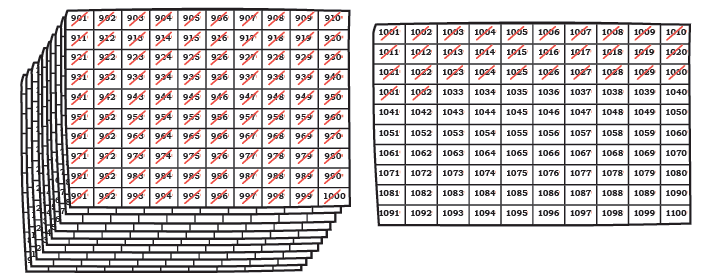
Let us see how they did it.
Q: How many people came for the community lunch? __________ 
Ans: 1032

Fill in the blanks with appropriate numbers.
Ans: 

Page 44 (Let Us Do)

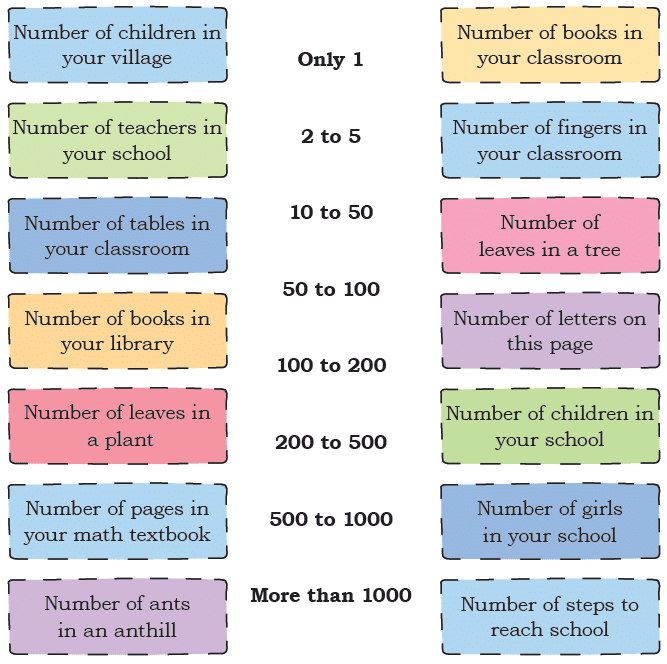
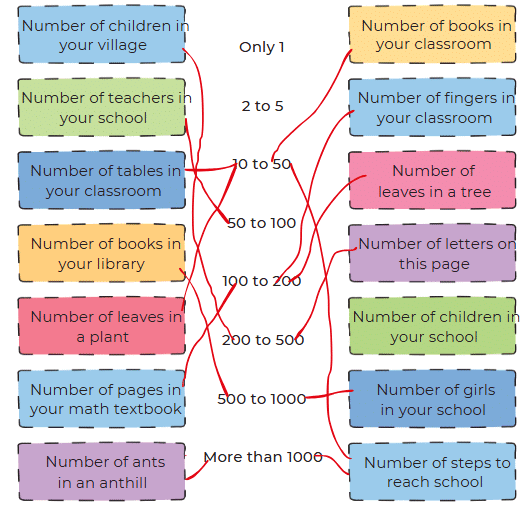
Q3: Identify the range of numbers most suitable for the following situations. Share your thoughts.
Ans:  

Q: Identify things around you that are more than 1000 in number.
Ans: Examples of things with more than 1000 in number:  

• Grains of rice in a sack  
• Stars in the sky  
• Leaves on a large tree  
• People in a big city

Page 47 (Let Us Break Up One-Thousand)

Q:
(a) We are at 900. How much more to make 1000? __________.
900 + ____ = 1000
Ans: 900 + 100 = 1000
So, 100 more is needed.

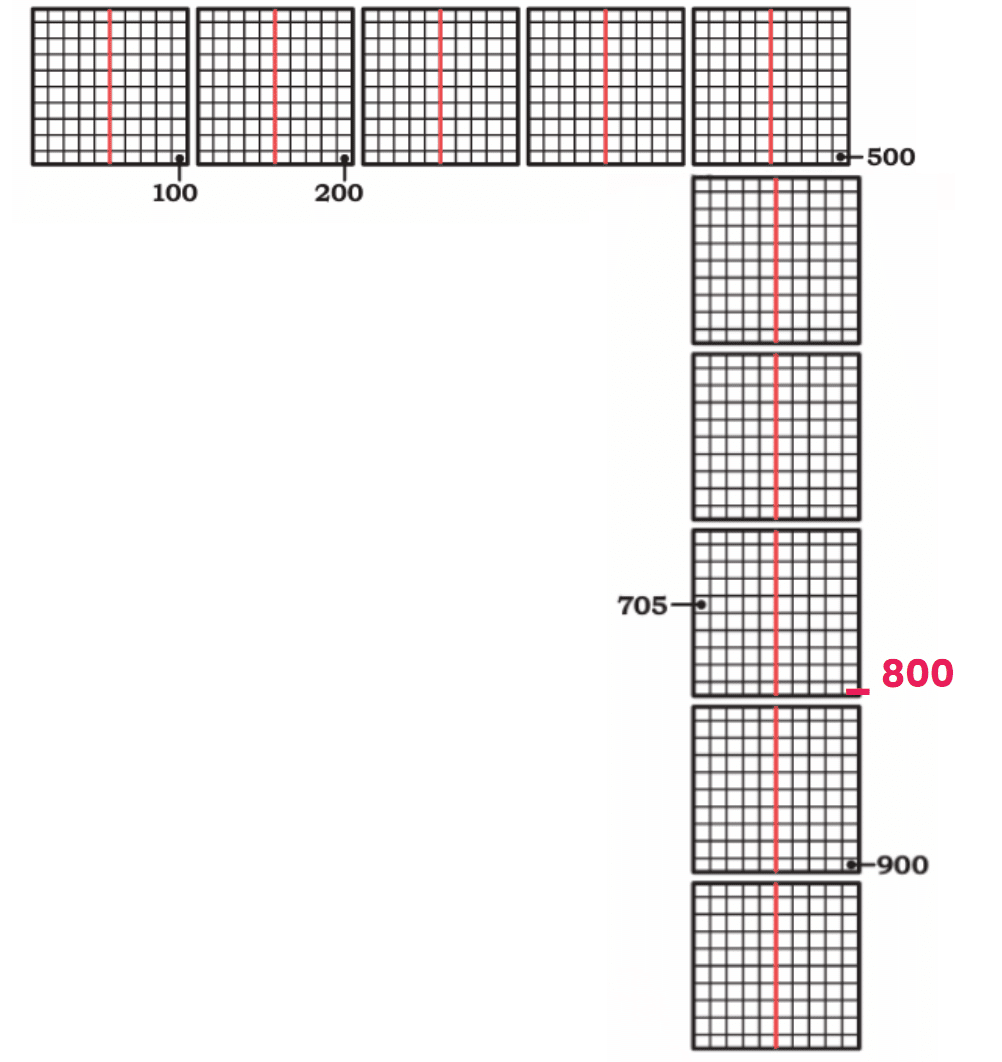
(b) Mark 800. How much more to make 1000?
800 + ______ = 1000
Ans: 800 + 200 = 1000
So, 200 more is needed.

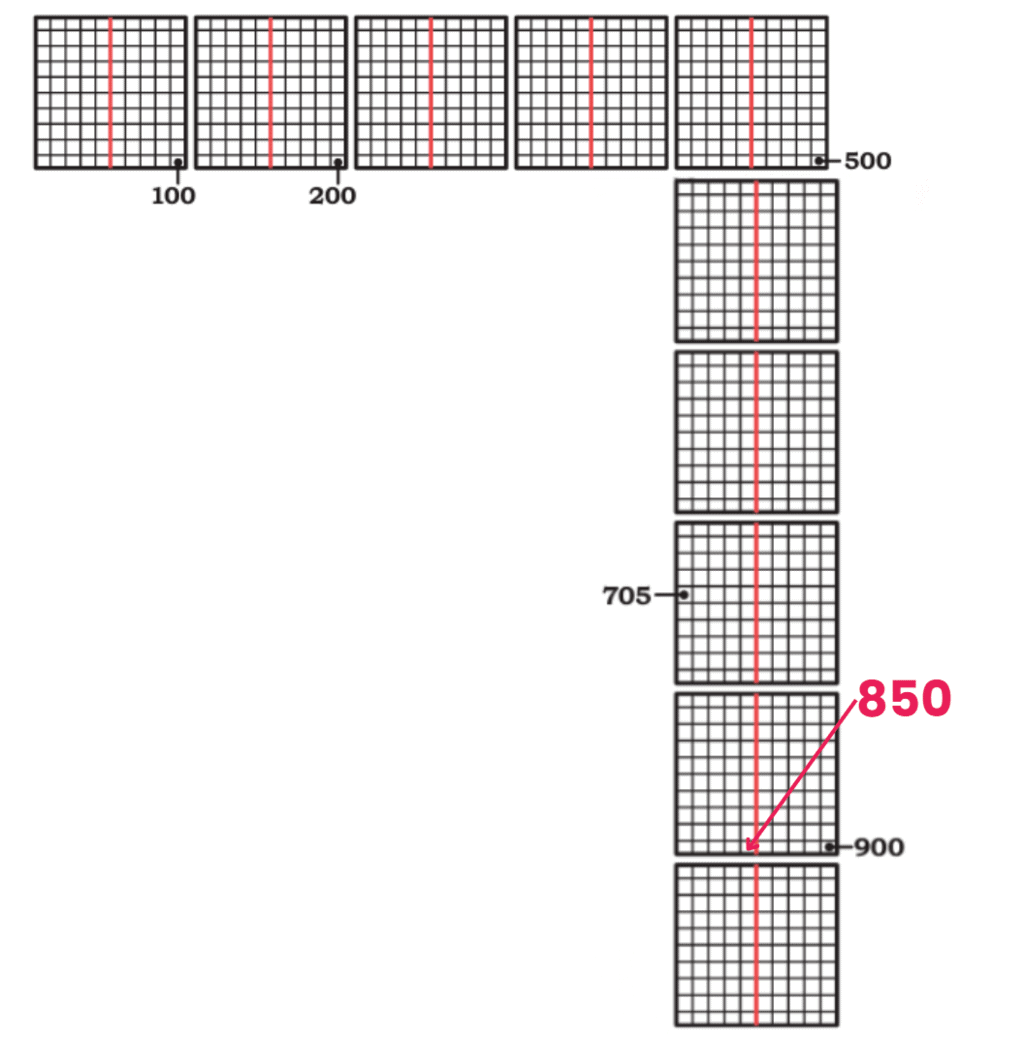
(c) Mark 850. How much more to 1000?
850 + ____ = 1000
Ans: 850 + 150 = 1000
So, 150 more is needed.

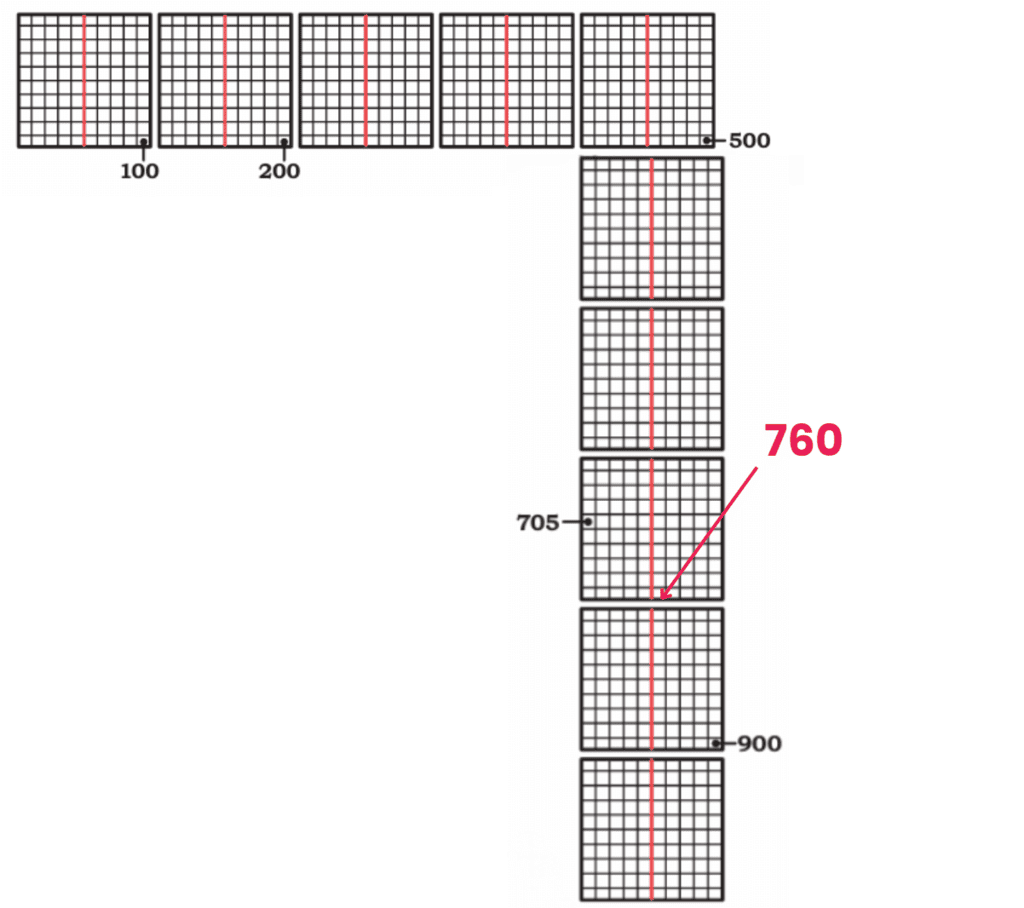
(d) Mark 760. How much more to 1000?
760 + _____ = 1000
Ans: 760 + 240 = 1000
So, 240 more is needed.

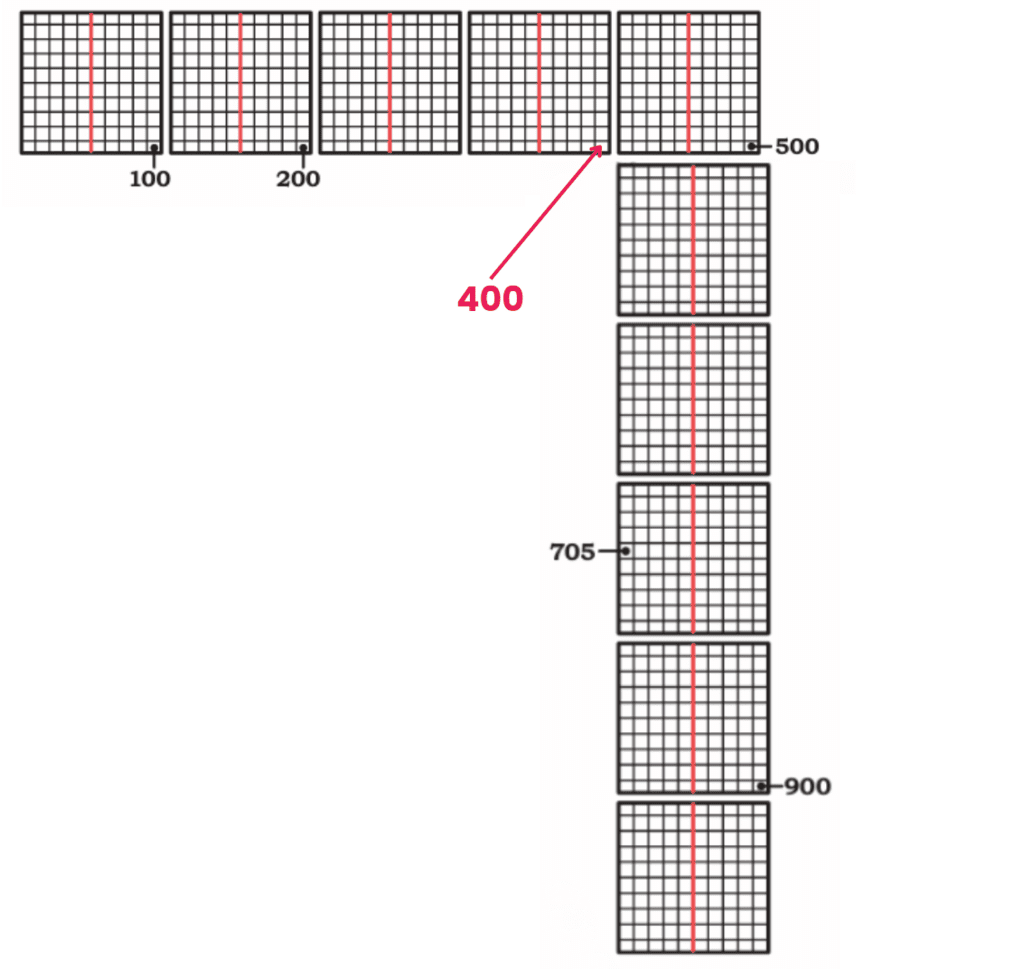
(e) Mark 400. How much less is 400 than 1000?
1000 – ____ = 400
Ans: 1000 – 600 = 400
So, 400 is 600 less than 1000.

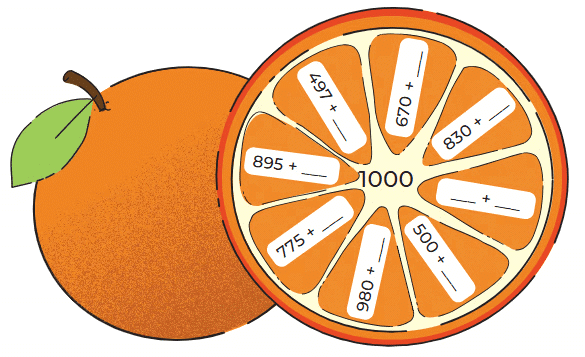
(f): Complete the addition facts leading to 1000.

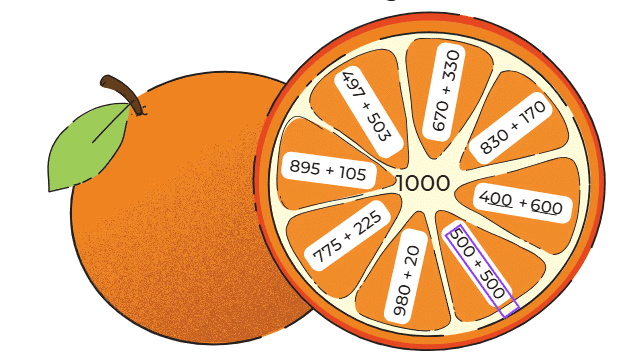
Ans: 

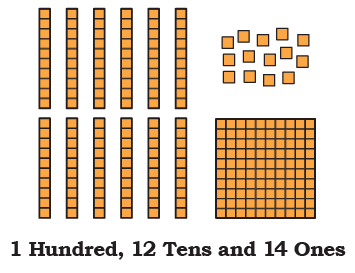
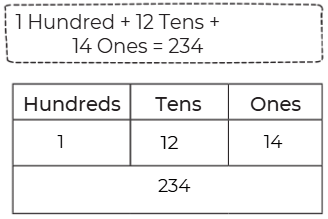
Page 48 (Grouping and Regrouping)

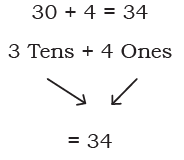
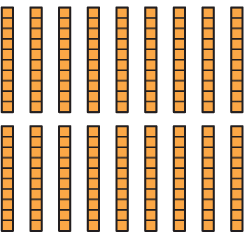
Look at the pictures below. Circle as many groups of 10 Ones or 10 Tens as possible. Write the final number against the following pictures.
Q1: 
Ans:

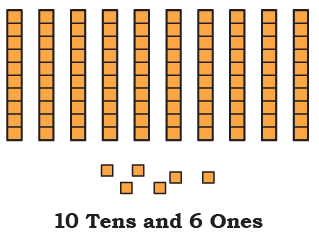
Q2: 
Ans: 200 + 50 = 250
2 Hundreds + 5 Tens + 0 Ones
= 250

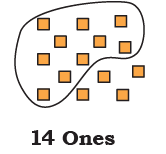
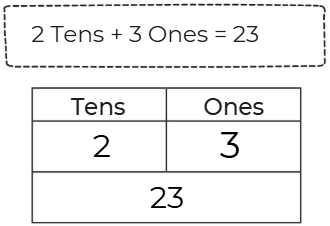
Q3: 
Ans: 20 + 5 = 25
2 Tens + 5 Ones = 25.
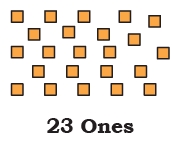
Q4: 
Ans: 100 + 80 = 180
1 Hundred + 8 Tens + 0 Ones = 180

Page 49 (Grouping and Regrouping)
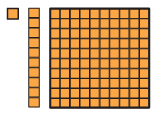
Circle groups of ten 1s, 10s, and 100s as many times as required in each of the following pictures. Fill in the empty boxes.
(a) Ans: 

(b) Ans: 

(c)
Ans: 

(d)
Ans:

(e) 
Ans: 

(f)
Ans:
Page 50 (Let Us Solve)
Identify and write the numbers for each of the following in your notebook. Draw pictures like these, if needed.

(a) 45 Ones 
(b) 39 Ones 
(c) 35 Tens 
(d) 86 Tens 
(e) 10 Tens and 1 Ones 
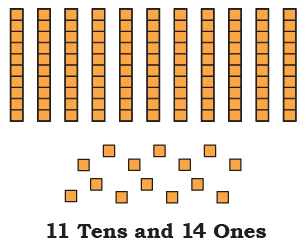
(f) 15 Tens and 23 Ones 
(g) 34 Tens and 12 Ones 
(h) 19 Tens and 10 Ones 
(i) 2 Hundreds, 13 Tens and 7 Ones
Ans: 
(a) 45
(b) 39
(c) 350
(d) 860
(e) 101
(f) 173
(g) 352
(h) 200
(i) 337

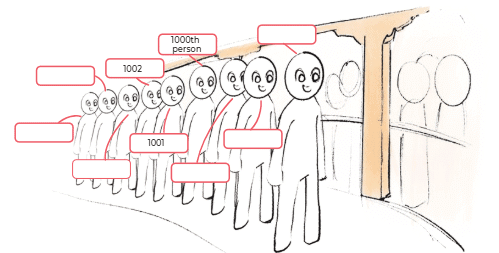
Page 51 (Numbers Beyond 1000 (One Thousand))

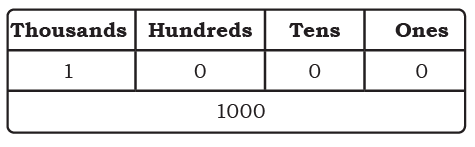
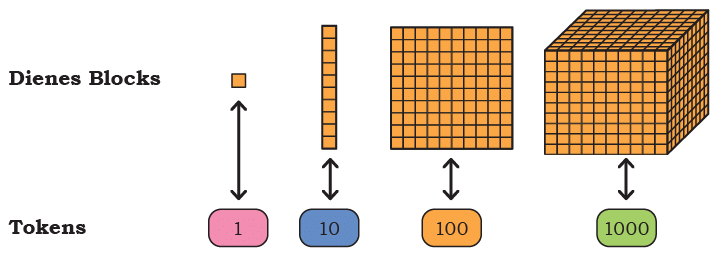
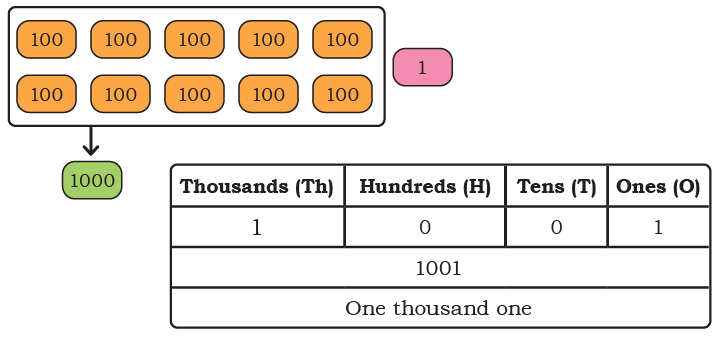
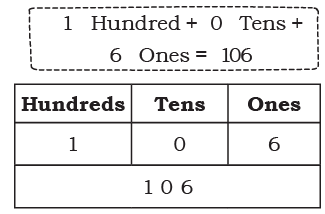
We will use tokens in place of Dienes blocks for larger numbers.

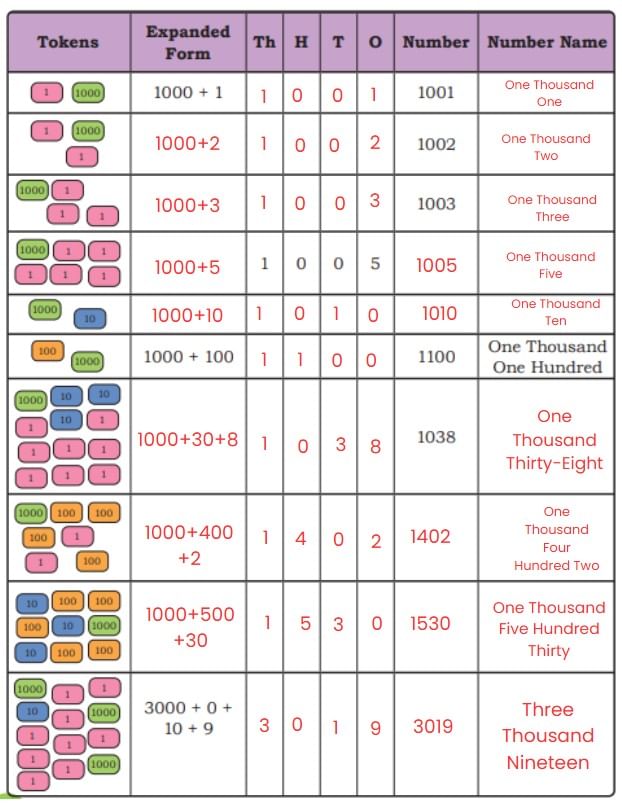
1 Thousand + 0 Hundred + 0 Tens + 1 Ones = 1001
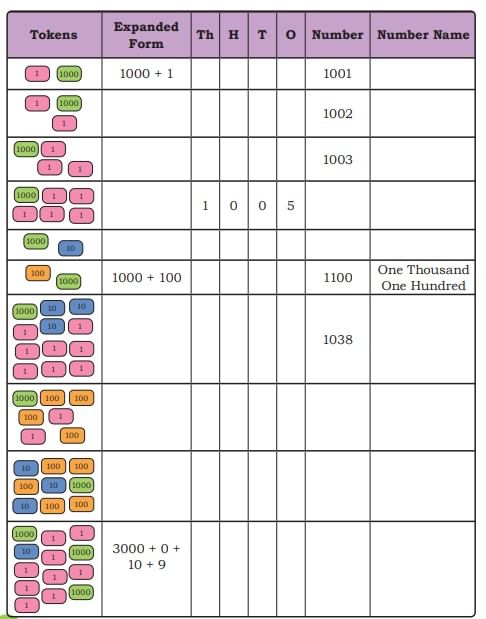
Look at the table below and fill in the blanks.
Ans: 

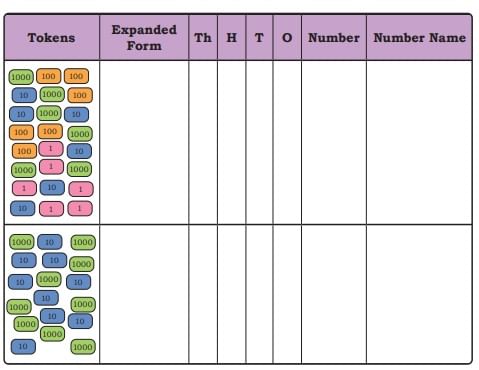
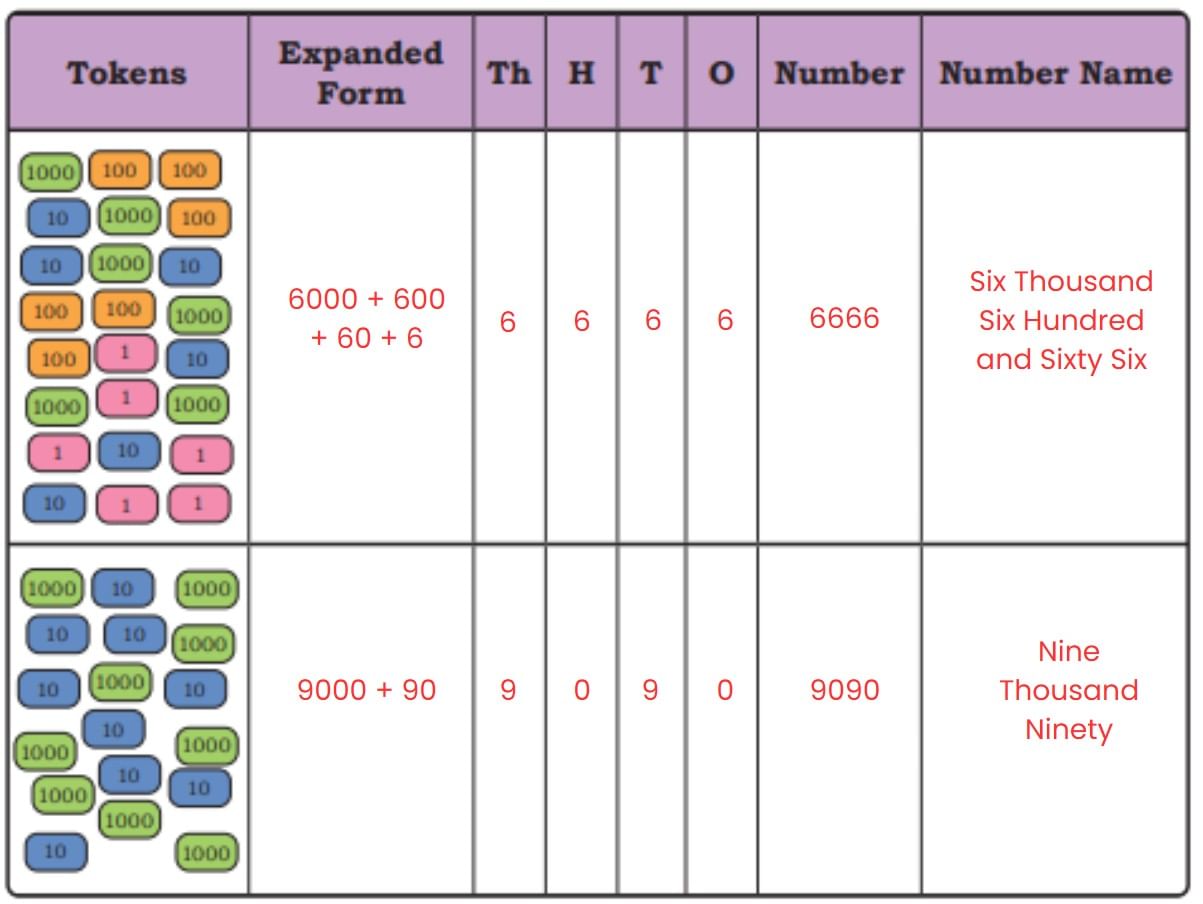
Ans: 

Page 53 

Q: Write the numbers in a sequence—forward and backward as indicated.
(a) 
Ans: 

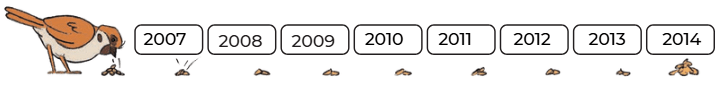
(b)
Ans:
 

(c) 
Ans: 

(d)

Ans: 

Page 54 (Let Us Play) 

Q: Make the place value slider. Children can take turns to increase or decrease the number as told.
(a) 1895 – increase the number by 1
Ans: 1895 + 1 = 1896

(b) 2785 – increase the number by 10
Ans: 2785 + 10 = 2795

(c) 3369 – decrease the number by 2
Ans: 3369 – 2 = 3367

(d) 5648 – decrease the number by 10
Ans: 5648 – 10 = 5638

(e) 6487 – increase the number by 20
Ans: 6487 + 20 = 6507

Page 54 (Let Us Think)

Q1: Ram wrote 7 Thousand 0 Hundreds 2 Tens 4 Ones as 724. Is this correct? Write the correct number.
Ans: 7 Thousand 0 Hundreds 2 Tens 4 Ones = 7000 + 0 + 20 + 4 = 7024
Ram’s number 724 is incorrect.
Correct number: 7024

Q2: Richa wrote 5 Thousand 6 Hundreds 0 Tens 3 Ones as 563. Is this correct? Write the correct number.
Ans: 5 Thousand 6 Hundreds 0 Tens 3 Ones = 5000 + 600 + 0 + 3 = 5603
Richa’s number 563 is incorrect.
Correct number: 5603

Page 55 (Number Line)

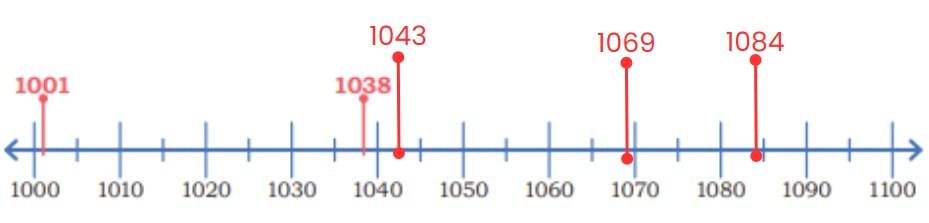
Q1: Which of these numbers lie between 2226 and 3226? Circle the correct answers.
Ans: Numbers between 2226 and 3226 are:
2236, 3126, 3216Q2:
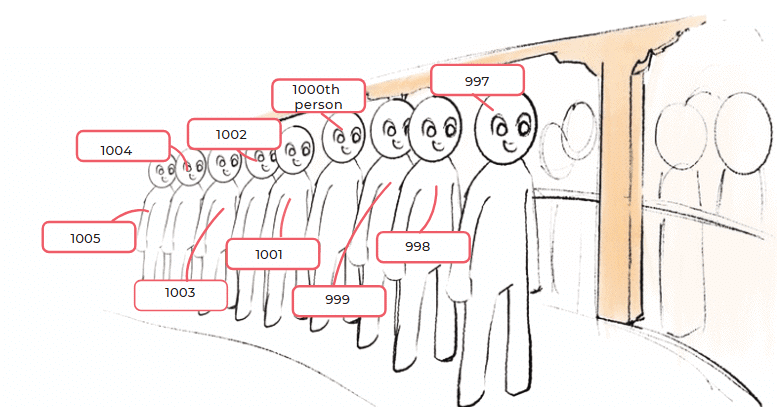
(a) 1001 and 1038 are marked on the number line. Try to mark 1043, 1069, and 1084 on the same number line.
Ans: 

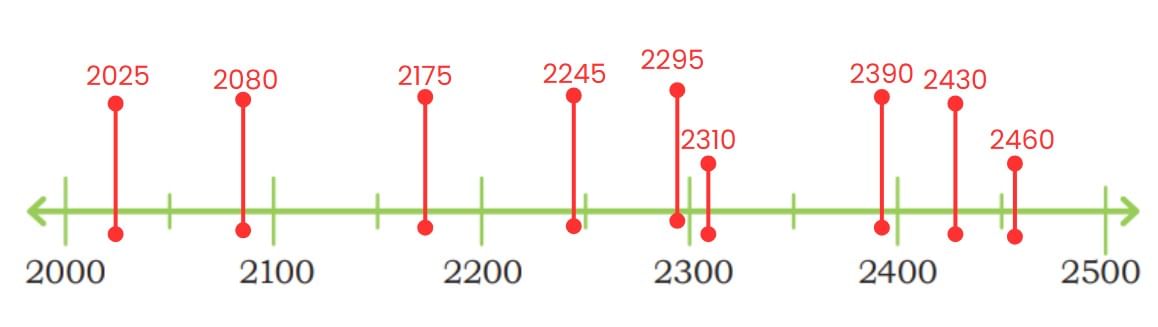
(b) Mark the following numbers on the number line below: 2025, 2080, 2175, 2245, 2295, 2310, 2390, 2430, 2460
Ans: 

(c) Mark the following numbers on the number line below: 5512, 5548, 5590, 5636, 5673, 5695
Ans: 

(d) Mark the following numbers on the number line below: 8679, 8990, 8923, 8763
Ans: 

Page 56 (Let Us Play)

Use the arrow cards (given at the end of the book) to make different numbers. Take turns giving a number for the grade to make using the arrow cards. Read aloud the number and express them in expanded form and in words.
3452 is made up of the cards 3000, 400, 50 and 2. 
The expanded form of 3452 is 3000 + 400 + 50 + 2. 
In words, 3452 is three thousand four hundred fifty two.
What cards are used to make 4085? Write it in expanded form and in words.
Ans: Cards used: 4000, 0, 80, 5

Expanded form: 4000 + 0 + 80 + 5

In words: Four thousand eighty-five

Page 56 (Find Me!)

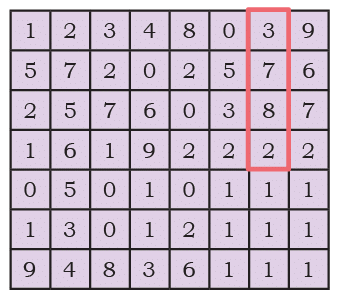
Read aloud the numbers and locate them in the grid.

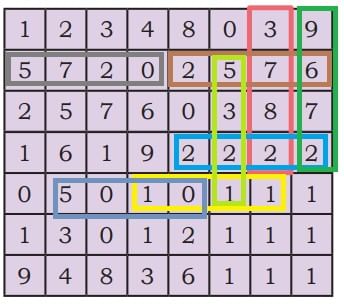
Ans:

Q1: The number 3782.
Ans: Already done

Q2: Two thousand five hundred and seventy-six.
Ans: 2576 is found in the grid

Q3: A 4-digit number with all digits the same.
Ans: 2222 is found in the grid:

Q4: The smallest 4-digit number in this table.
Ans: The smallest 4-digit number is 1011.

Q5: The largest 4-digit number in this table.
Ans: The largest 4-digit number is 9672

Q6: A number more than 5000 and less than 5200.
Ans: 5010 is found in the grid

Q7: A number between 5600 and 6300.
Ans: 5720 number between 5600 and 6300 in the grid.

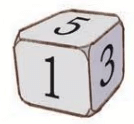
Q8: A 4-digit number all of whose digits can be found on a die.
Ans: A die has digits 1 to 6. A possible number is 5321 

Page 57 (Let Us Solve)

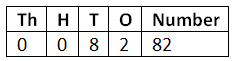
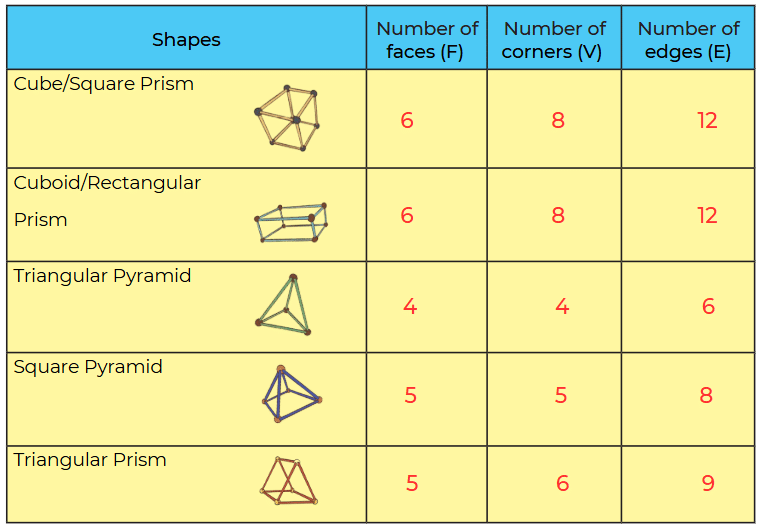
Q1: Use tokens of 1s, 10s, 100s, 1000s to identify the numbers and write them in the table.
(a) 6 Tens and 22 Ones
Ans: 6 Tens = 60, 22 Ones = 22
Total = 60 + 22 = 82  

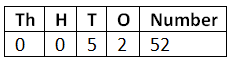
(b) 4 Tens and 12 Ones
Ans: 4 Tens = 40, 12 Ones = 12
Total = 40 + 12 = 52  

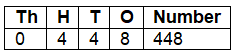
(c) 3 Hundreds, 14 Tens, and 8 Ones
Ans:3 Hundreds = 300, 14 Tens = 140, 8 Ones = 8
Total = 300 + 140 + 8 = 448  

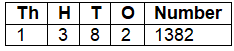
(d) 12 Hundreds, 18 Tens, and 2 Ones
Ans: 12 Hundreds = 1200, 18 Tens = 180, 2 Ones = 2
Total = 1200 + 180 + 2 = 1382  

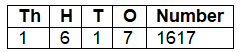
(e) 1 Thousand, 5 Hundreds, 10 Tens, and 17 Ones
Ans: 1 Thousand = 1000, 5 Hundreds = 500, 10 Tens = 100, 17 Ones = 17
Total = 1000 + 500 + 100 + 17 = 1617  

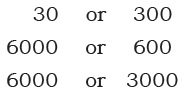
Q2A: Circle the number that is bigger.

Ans:  

• 30 or 300: 300 
• 6000 or 600: 6000  
• 6000 or 3000: 6000

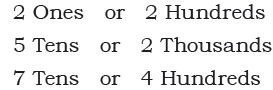
Q2B: Circle the number that is smaller.

Ans:  

• 2 Ones or 2 Hundreds: 2 Ones
• 5 Tens or 2 Thousands: 5 Tens
• 7 Tens or 4 Hundreds: 7 Tens

Page 58 (Comparing Numbers)

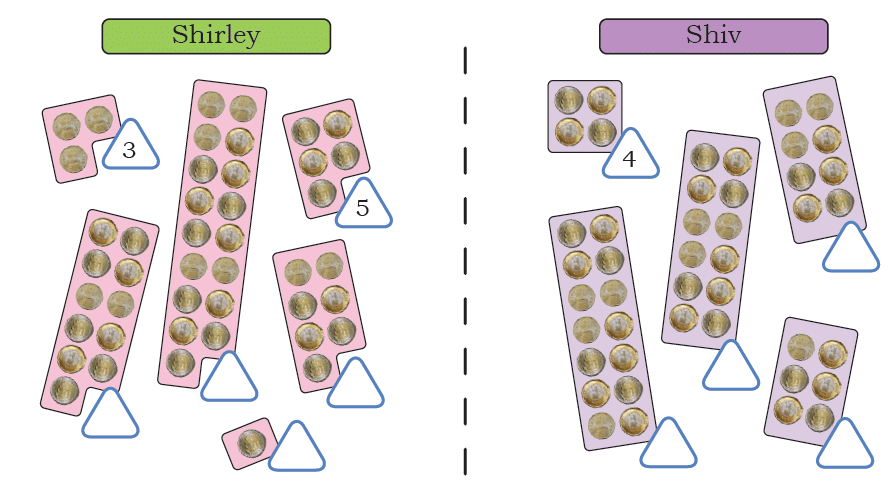
Jaspreet and Gulnaz help to keep a record of the number of plates used in the Gurudwara every month. Use the signs <and> to find the month when a larger number of plates were used.

Ans: 

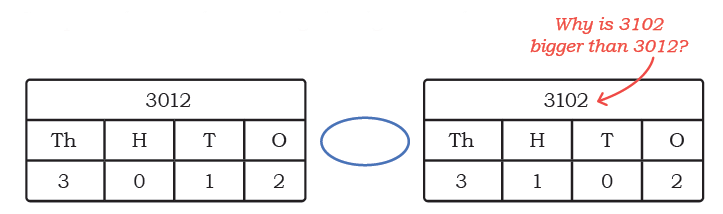
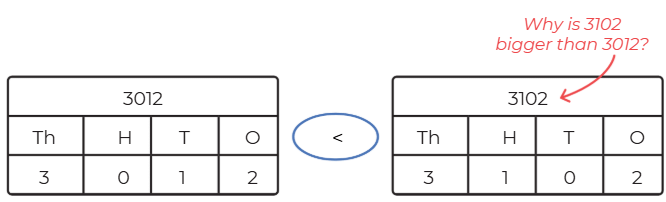
Q: Compare the numbers using the signs <and>.
Describe how you decided which number is the bigger one. Which position (Th, H, T, O) helped you to decide this?
Ans: 
3012 < 3102
3102 is bigger than 3012 because the hundreds place in 3102 has 1 hundred, while 3012 has 0 hundreds. The thousands, tens, and ones places are the same.

Page 58 (Let Us Do)

Compare the following pairs of numbers using < and >. Make a Th, H, T, O table, if necessary. Share your thoughts with the class.
(a) 2190 ______2910
Ans: 2190 < 2910
(Th: 2 vs 2, H: 1 vs 9, 1 < 9, so 2190 is smaller)

(b) 7087 ______ 7088
Ans: 7087 < 7088
(Th: 7 vs 7, H: 0 vs 0, T: 8 vs 8, O: 7 vs 8, 7 < 8, so 7087 is smaller)

(c) 1009______ 9001
Ans: 1009 < 9001
(Th: 1 vs 9, 1 < 9, so 1009 is smaller)

(d) 982 ______ 1024
Ans: 982 < 1024
(Th: 0 vs 1, 0 < 1, so 982 is smaller)

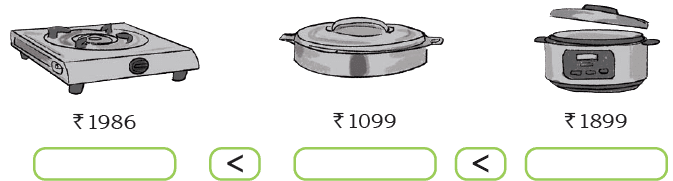
Q2: Order the prices of the following objects from smallest to biggest (increasing order)
Ans:

Q3: The following women international cricketers have played 200 ODIs (One-Day International Matches). Listed below are their scores. Arrange the runs scored by them in increasing order (from lowest to highest).
Ans: 4064 < 4814 < 5114 < 6002 < 7805

Page 60 (Let Us Do)

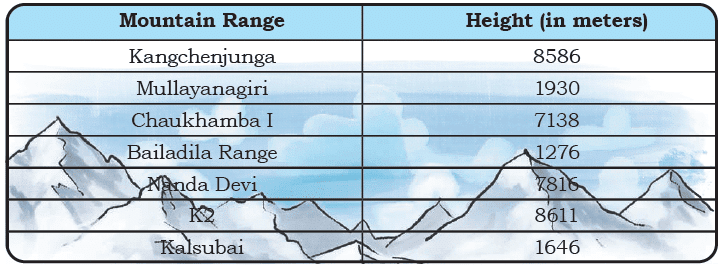
Q4: Arrange the following mountain ranges in decreasing order of height (from highest to lowest).

Ans: 

• K2: 8611 meters
• Kangchenjunga: 8586 meters
• Nanda Devi: 7816 meters
• Chaukhamba I: 7138 meters
• Mullayanagiri: 1930 meters
• Kalsubai: 1646 meters
• Bailadila Range: 1276 meters

Q5 Use the signs <, =, > to compare the following.
(a) 2 Tens + 4 Thousands + 3 Hundreds _____ 2043
Ans: 2 Tens + 4 Thousands + 3 Hundreds = 4000 + 300 + 20 = 4320
4320 > 2043

(b) 2 Tens + 4 Thousands + 3 Hundreds _____ 4320
Ans: 2 Tens + 4 Thousands + 3 Hundreds = 4320
4320 = 4320

(c) 2 Thousands + 9 Hundreds + 9 Tens + 9 Ones _____ 3000
Ans: 2 Thousands + 9 Hundreds + 9 Tens + 9 Ones = 2000 + 900 + 90 + 9 = 2999
2999 < 3000

(d) 15 Ones + 9 Tens + 3 Hundreds _____ 1593
Ans: 15 Ones + 9 Tens + 3 Hundreds = 300 + 90 + 15 = 405
405 < 1593

(e) 5000 + 30 + 4 _____ 5034
Ans: 5000 + 30 + 4 = 5034
5034 = 5034

(f) 5000 + 300 + 4 _____ 5340
Ans: 5000 + 300 + 4 = 5304
5304 < 5340

Q6 Fill the blanks with digits 0 –9 such that the numbers meet the condition.
(a): 7__ __3 < 768__
Ans:

• We have 7 _ _ 3 on the left and 768 _ on the right. The “<” means the first number must be smaller than the second.
• The first number starts with 7 and ends with 3, but the middle two spots are blank. The second number is 768 with one blank at the end.
• Both numbers start with 7, so we need to look at the next digits to make sure 7 _ _ 3 is smaller than 768 _.
• For 768 _, the last digit can be anything (like 7680, 7681, 7682, etc.). But we need to make the first number smaller.
• In 7 _ _ 3, the second digit (first blank) should be 0, 1, 2, 3, 4, 5, or 6. Why? Because numbers like 7033, 7133, 7233, up to 7633 are all smaller than 7680 (or any 768_ number).
• The third digit in 7 _ _ 3 can be anything (0–9), but the second digit is the important one to keep it smaller.

The first blank in 7 _ _ 3 can be 0, 1, 2, 3, 4, 5, or 6.

(b) 853__ < 8__3__
Ans: 

• We have 853 _ on the left and 8 _ 3 _ on the right. We need 853 _ to be smaller than 8 _ 3 _.
• Both numbers start with 8, so we look at the next digits.
• In 853 _, the second digit is 5. In 8 _ 3 _, the second digit is a blank.
• To make 8 _ 3 _ bigger than 853 _, the second digit of 8 _ 3 _ must be bigger than 5. So, it can be 6, 7, 8, or 9.
• That makes numbers like 863_, 873_, 883_, or 893_, which are all bigger than 853_ (like 8530, 8531, etc.).
• The last digits in both numbers can be anything (0–9), but the second digit of 8 _ 3 _ is what matters most.

The first blank in 8 _ 3 _ can be 6, 7, 8, or 9.

(c) __2__1 < 5__2__
Ans: 

• We have _ 2 _ 1 on the left and 5 _ 2 _ on the right. We need _ 2 _ 1 to be smaller than 5 _ 2 _.
• The second number starts with 5, so it’s like 502_, 512_, 522_, etc., depending on the blank.
• The first number has a 2 in the second spot and a 1 at the end, so it’s like _ 2 _ 1. The first and third digits are blank.
• Since 5 (in 5 _ 2 _) is bigger than anything starting with 1, 2, 3, or 4, we can make the first number start with a small digit like 1, 2, 3, or 4.
• For example:
  • If the second number is 502 _, the first number can be 1211, 2211, etc., because 1211 < 5020 or 2211 < 5020.
  • If the second number is 512 _, the first number can be 1211, 2211, etc., because 1211 < 5120 or 2211 < 5120.
• The third digit in _ 2 _ 1 and the last digit in 5 _ 2 _ can be anything (0–9), but the first digit of _ 2 _ 1 should be small.

The first blank in _ 2 _ 1 can be 1, 2, 3, or 4, and the first blank in 5 _ 2 _ can be 0, 1, 2, 3, or 4 to make pairs that work.

Example: If we pick 1211 and 5120, then 1211 < 5120, which is true!

Page 61 (Challenge!)

Q: There are 99 numbers strictly between 700 and 800 excluding 700 and 800. How many numbers are there strictly between 7000 and 8000? Circle the correct answer: 
Ans: Numbers between 700 and 800 (excluding 700 and 800) are 701 to 799, which is 799 – 701 + 1 = 99 numbers.
Numbers between 7000 and 8000 (excluding 7000 and 8000) are 7001 to 7999, which is 7999 – 7001 + 1 = 999 numbers.

Let Us Explore

Q1: Make as many four-digit numbers as possible using the digits 2, 3, 4, 7 without repetition. There are 24 different numbers possible. Find as many as you can and arrange the numbers in decreasing order in your notebook.
Ans: Using digits 2, 3, 4, 7 without repetition, the possible 4-digit numbers are (24 permutations):
7432, 7423, 7342, 7324, 7243, 7234, 4732, 4723, 4372, 4327, 4273, 4237,
3742, 3724, 3472, 3427, 3274, 3247, 2743, 2734, 2473, 2437, 2374, 2347
Arranged in decreasing order:
7432 > 7423 > 7342 > 7324 > 7243 > 7234 > 4732 > 4723 > 4372 > 4327 > 4273 > 4237 > 3742 > 3724 > 3472 > 3427 > 3274 > 3247 > 2743 > 2734 > 2473 > 2437 > 2374 > 2347

Q2: Compare with your friends to find what other numbers they have made. See if all of you together can come up with all the 24 numbers. How do you know that you have all possible such numbers?
Ans:  Do it Yourself!

Page 34: Let Us Count

Gundappa has some land with tall coconut trees.

Q1: How many coconut trees does Gundappa have?
Ans: Gundappa has 81 coconut trees.

Q2: How do you know?
Ans: I counted the number of trees in each row and each column. There are 9 rows and 9 columns. So, the total number of trees is 9 × 9 = 81.

Q3: Gundappa has plucked 5 coconuts from each tree. How many coconuts has he plucked?
Ans: Gundappa has plucked 81 × 5 = 405 coconuts.

Q4: Muniamma makes plates and cups. 

Number of cups = ________
Ans: In the first stack, from top to bottom, there are 11 cups. Similarly, in the second, third, fourth, fifth and sixth stacks, there are 10, 9, 9, 10 and 11 cups, respectively.
So, the total cups are:
11 + 10 + 9 + 9 + 10 + 11 = 60 cups

Muniamma has arranged coconut laddoos and milk peda in trays like this. All trays have the same arrangement. Trays are placed one on top of the other.

Q5: How many coconut laddoos are there in the trays?
Ans: Each tray has 13 coconut laddoos. There are 3 trays.
So, 13 × 3 = 39 coconut laddoos.

Q6: How many milk pedas are there in the trays?
Ans: Each tray has 12 milk pedas. There are 3 trays.
So, 12 × 3 = 36 milk pedas.Page 35: Patterns with Money

Shirley and Shiv arranged their play money in some nice patterns as shown below.

Q1: How much money? (Left pattern)
Ans: ₹80

Q2: How much money? (Right pattern)
Ans: ₹108

 Q3: How did you count them? 

Ans: Left Pattern:

 There are 4 coins of ₹10 and 1 coin of ₹20 and 4 coins of ₹5.
So, total money = (4 × 10) + 20  + (5 x 4)= ₹80.

Right Pattern:

₹2 coins = 4
₹5 coins = 8
₹10 notes = 6
So, total money = (4 × 2) + (8× 5) + (6 × 10) = 8 + 40 + 60 = ₹108.

Q4: Arrange play money of amounts ₹1, ₹2, ₹5, and ₹10 to show ₹36, ₹125, and ₹183. Ask your peers to tell how much it is.
Ans:To make ₹36:

• ₹10 notes × 3 = ₹30
• ₹5 coin × 1 = ₹5
• ₹1 coin × 1 = ₹1
• Total = ₹30 + ₹5 + ₹1 = ₹36

To make ₹125:

• ₹10 notes × 10 = ₹100
• ₹5 coin × 5 = ₹25
• Total = ₹100 + ₹25 = ₹125

To make ₹183:

• ₹10 notes × 15 = ₹150
• ₹5 coin × 5 = ₹25
• ₹2 coin × 4 = ₹8
• Total = ₹150 + ₹25 + ₹8 = ₹183

Page No 35: Two Ways

Shirley and Shiv arranged their coins in the following ways. Write the number of coins in the triangles.

Ans:

Q1: Describe Shiv’s arrangement and write his numbers.

Ans: Shiv has arranged his coins in even numbers. The numbers are 4, 6, 8, 12 and 14.

Q2: Describe Shirley’s arrangement and write her numbers.
Ans: Shirley has arranged her coins in odd numbers. The numbers are 1, 3, 5, 7, 11 and 17.

Q3: Identify numbers between 1 and 20 as even or odd. You may draw the pairing arrangement of the numbers.
Ans: Odd numbers between 1 and 20: 1, 3, 5, 7, 9, 11, 13, 15, 17, 19
Even numbers between 1 and 20: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20

We can pair even numbers equally. Odd numbers always leave one unpaired.

Q4: Do you think all numbers in the times-2 table are even?
Ans: Yes, all numbers in the 2 times table are even.
For example: 2, 4, 6, 8, 10, 12… All these can be made into equal pairs without any left.Page 37: Crayons Arrangement

Q: Circle the odd numbers and put a square around each even number. Use the crayons arrangement, if needed.


Ans: The numbers given are 36, 37, 38, 39, 8, 5, 51, 52, 43, 69.

To check, pair crayons for each number. For example, 37 crayons leave one unpaired (odd), while 38 crayons can be fully paired (even).

Q: Explore your textbook and find out what Shirley has seen. Draw a square on the even numbers. Put a circle on the odd numbers.
Ans: Do it yourself.Page 38 – Crayons Arrangement (Continued)

Q: Identify which of the following numbers are even and which are odd. Explain your reasoning.
Ans: Even numbers: 30, 46, 78, 300, 154.

• Reasoning: These numbers can be paired completely. For example, 30 can be divided into 15 pairs (30 ÷ 2 = 15), so it is even.

Odd numbers: 67, 415, 99.

• Reasoning: These numbers cannot be paired completely. For example, 67 leaves one unpaired (67 ÷ 2 = 33 with remainder 1), so it is odd.

Q: Make two 2-digit numbers using the digits 1 and 6 without repetition. Identify the numbers as even or odd.
Ans:

• Numbers: 16, 61.
• 16 is even (can be paired, 16 ÷ 2 = 8).
• 61 is odd (cannot be paired, 61 ÷ 2 = 30 with remainder 1).

Q: Now choose any two digits and make 2-digit numbers in such a way that the numbers are even.
Ans: Choose digits 2 and 4.

• Numbers: 24, 42.
• Both are even: 24 ÷ 2 = 12 (paired), 42 ÷ 2 = 21 (paired).

Q: Are there more even or odd numbers between 1 and 100?
Ans: There are 50 even numbers and 50 odd numbers between 1 and 100.

• Even numbers: 2, 4, 6, …, 100 (50 numbers).
• Odd numbers: 1, 3, 5, …, 99 (50 numbers).
  So, there are an equal number of even and odd numbers.

Q: Shirley notices that both the numbers, before and after an odd number, are even.
Ans: This is true. For example, for the odd number 5, the number before (4) and after (6) are even. Odd numbers (e.g., 1, 3, 5, …) are not divisible by 2, while the numbers before and after (e.g., 4 and 6 for 5) are divisible by 2, making them even.

Q: Shiv wonders if both the numbers, before and after an even number, will be odd. What do you think? Check and discuss.
Ans: Yes, this is true. For example, for the even number 4, the number before (3) and after (5) are odd. Even numbers (e.g., 2, 4, 6, …) are divisible by 2, while the numbers before and after (e.g., 3 and 5 for 4) are not divisible by 2, making them odd.

Q: Choose any 10 numbers in order without skipping any (consecutive numbers). Write whether they are even or odd below each number. What do you notice? Discuss.
Ans: Choose numbers 20 to 29:

• 20 (even), 21 (odd), 22 (even), 23 (odd), 24 (even), 25 (odd), 26 (even), 27 (odd), 28 (even), 29 (odd).
• Notice: The numbers alternate between odd and even (even, odd, even, odd, even, …). This happens because each number increases by 1, switching between not divisible by 2 (odd) and divisible by 2 (even).

Where Are You Hiding?(Page 24)

Let Us DoQ1: Look at the picture and answer the following:
a. Which game are the children playing?
Ans: The children are playing ‘hide and seek’ game.

b. Who is looking from the top?
Ans: Jagat is looking from the top.

c. In Scene 1, if Rani faces towards the hut, will she be able to see who all are hiding near the hut? Discuss.
Ans: In scene 1, if Rani faces towards the hut, she will not be able to see who all are hiding near the hut because Bholu is hiding behind the tree and Mini is hiding behind the hut.

Discuss(Page 25)In Scene 4, can Mini see all the children playing the game? Discuss.
Ans: No, Mini can only see Bholu and Jagat.

Q2: Mini, Bholu, and Rani draw the same brick. Why are their drawings of the same brick different? Discuss.Ans: Their drawings are different because they drew the brick from different views. Mini drew the front view, Bholu drew the top view, and Rani drew the side view. Each view shows a different side of the brick.

Whose drawing shows the following views?

Ans:

Q3: Look at the pictures and name the objects. Also write which view of the object is given.

Ans: 

Q4. Jagat and Rani have made different drawings of the same objects. Match the views with the objects.
Look around you! Try to make drawings of objects, such as chairs, tables, pencils, erasers, birthday cap, and bottle from different views.
Ans: 

Boxy Buildings(Page 27)Jagat and Mini are playing. They are making different buildings using empty matchboxes and making their drawings from different views.

Now, you also collect empty matchboxes or any other empty boxes to create different buildings and draw their top, side, and front views. You can challenge your friends by asking them to match your drawing with the right building.
Ans: Do it Yourself.

Cat Finds Jagat(Page 28)The next day, the five friends go to school feeling excited as it is an activity day. Jagat’s pet cat follows him to school. The cat sits on the window and tries to find Jagat.

Let Us DoJagat’s cat sees him sitting on the third desk in the first row .
Q1: Mark Jagat’s position in the picture.
Ans: 

Q2: Describe the position of the blue bag.
Ans: The blue bag is on the first desk in the first row.

Q3: What do you see on the middle desk of the second row?
Ans: A red bottle is on the middle desk of the second row.

Q4: Where is the notebook kept – the first desk in the second row or the middle desk in the third row?
Ans: The notebook is on the middle desk in the third row.

Q5: Draw an apple on the third desk of the second row.
Ans: 

Grid Game(Page 29)

Q: Here are the clues given by Rani to fill the grid: 

•  An eraser at the top right corner. 
• A pencil in the top left corner. 
• An apple in the middle of the second row and second column. 
• A water bottle in the third row and second column.

Ans: 

Grid Game – Treasure Hunt(Page 30)In this game, one player has to think of an object from the grid and help the other player locate it. Let’s see how Jagat and Mini are playing.

What object did Jagat think of?
Ans: 

• Mini takes 2 steps to the left and 1 step upwards. She reaches the Cat.
• Mark Mini’s position on the grid.
  
• Jagat thought of object mango.

Play the game with your partner 
From the starting point, trace the paths to reach the flower. How many steps are required for each path? Speak out or write down the different paths followed to reach the flower.
Ans: Steps required for each path (Path 1 and Path 2) = 7 steps

From the starting point, where would you reach in a smaller number of steps: the mango or the orange?

Steps required to reach mango = 5 steps.

Steps required to reach orange = 4 steps

Orange can be reached in smaller number of steps.

Drone Around the School(Page 31)Gyan has got a drone to show her friends. A drone can take pictures while flying.

Q: Circle the places or things that you see in the picture and write their names.
Ans: In the drone’s picture, circle items or places like trees, buildings, or playgrounds. Their names, e.g., “Tree, Car, School, Playground.”

Drone Around the School (Continued)(Page 32) Preet’s elder sister has made a sight map of the school. You can easily locate Grade 4 on the map.
 Q1: Trace the path from the Grade 4 classroom to the stage.
Ans: 

Q2: How many routes were you able to find? (You may use different colour pencils to trace the different routes)
Ans: Number of routes to go from the Grade 4 classroom to the stage = 5 routes

Q3: Which is the shortest route? How do you know?
Ans: The route which is going to the right of Grade 4 via playground is the shortest.

Q4: The water delivery man has turned left from the entrance. Help him reach MDM Kitchen by telling him the route. Write the directions below.
Ans: Directions to the MDM Kitchen from the entrance: 
(i) Turn left at the entrance and walk straight. 
(ii) Go along the path between the Principal’s Office and the Stage. 
(iii) Keep walking straight until you reach the Medical Room. 
(iv) From the Medical Room, turn left. The MDM Kitchen will be right there.

Q5: Rajat is not feeling well. Which way will you choose to take him to the medical room from the library?
Ans: (i) Walk past the stage and enter the corridor next to the hall. 
(ii) Continue straight, passing the Middle Wing classrooms. 
(iii) The room at the far-left corner of the corridor is the Medical Room.

Q6: After the assembly in the playground, Bholu must go to the IT room and Rani has to go to the sports room. Trace their paths. Which way is longer?
Ans: So, Rani’s way is longer.

Let Us Do (Project Work)(Page 33)Q: Draw a sight map to show the way from your school entrance to your classroom and any other important places.
Ans: Do it Yourself.