Introduction
Imagine a world full of measuring tools and colorful adventures! In this chapter, we’ll learn how to measure using our hands, feet, and special tools like metre ropes. Get ready to compare lengths, guess distances, and have a fun as we explore the exciting world of measurement together!
Let’s Understand With a Story
Once there were two friends, Riya and Aryan. They loved playing cricket. One day, they wanted to know how long their cricket bat was.

Riya & Aryan
Aryan tried to measure it using his hands and said it was 4 hand lengths long.

Then, Riya tried and said it was 6 hand lengths long for her.
They were confused why the bat was different lengths for each of them.

Their mom explained, “Your hands are different sizes, so using hand length isn’t a good way to measure. You should use a ruler or a measuring tape. They give the same answer for everyone.”
Riya and Aryan understood and learned that using the right tools helps us measure things correctly.
From that day on, they always used a ruler or measuring tape to measure things accurately.
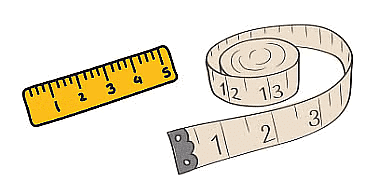
Ruler & Measuring Tape
Now that we know why and how measurement is important, let’s understand different types of measurements.
Try yourself:
What is the most accurate way to measure the length of an object?
- A.Using hand lengths
- B.Using a ruler or measuring tape
- C.Guessing the length
- D.Comparing with other objects
View Solution
Measurement of Length – “How long?”
Have you ever wondered how people measured things long ago? They didn’t have rulers like we do now. Instead, they used parts of their bodies! Here are some of the parts they used:
- A hand span is the distance from the tip of the thumb to the tip of the little finger when the fingers are spread apart.
- A cubit is the distance from the elbow to the tip of the middle finger when the hand is stretched out.
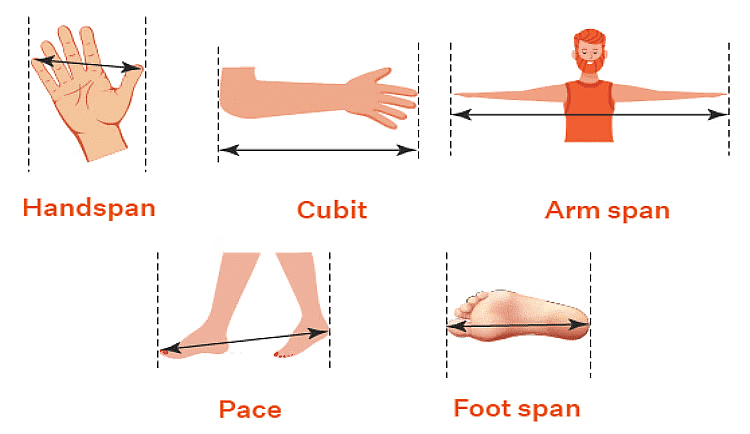

But here’s the thing: everyone’s hand span and cubit are different like we saw in the story given above.
So when they measure something, they don’t always get the same answer. That’s why mathematicians decided to create standard units of length.Foot Scale
- In many parts of the world, people used units like inches, feet, and yards.
- 12 inches make one foot and 3 feet (plural of foot) make 1 yard.
- But now, we mostly use the Metric system.
- The standard unit for measuring length is called a meter, and we write it as ‘m’.
- Longer distances are measured in kilometers (km), and smaller lengths in centimeters (cm).
So, even though people used to measure with their hands and arms, now we use meters and centimeters to measure things accurately!
For measuring lengths, we use:
- a Meter rod,
- a Measuring tape
- a Ruler.
Different tools for Measuring Lengths

A cloth merchant measures cloth by iron rod called the meter rod.
Metre Rod

15 cm Ruler
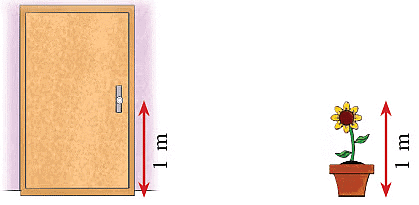

Here, the distance from the floor to a door knob is about 1 meter and the height of the plant is also about 1 meter.
There are certain things such as the following that are more than a meter long.
There are certain things like those shown below that are less than a meter long.
We use meter to measure long length and centimeter to measure short length.
Measurement of Length Using Centimeter Scale
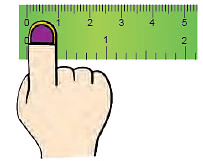

Your finger is about 1 centimeter wide.
This will help you to estimate length in centimeter. A 15 cm or 30 cm ruler is used to measure lengths in centimeter.
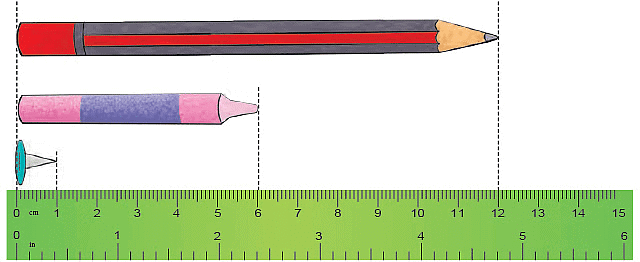
To measure the length of an object, say, a sharpener, line up one of the sharpener end at the 0 mark of the ruler. The other end, touches the 2 cm mark of the ruler, so it is 2 cm long.
Similarly, we can measure the length of the following objects
- The length of the pencil is 12 cm.
- The length of the crayon is 6 cm.
- The length of the board pin is 1 cm.

Try yourself:
What is the standard unit for measuring length in the Metric system?
- A.Inch
- B.Foot
- C.Meter
- D.Yard
View Solution
Measuring Distances – “How far?”
Measuring distance is like counting steps or jumps to find out how far things are from each other on a grid or map. We use units of distance, like meters, feet, km to measure the length or distance between two points.
Long distances measured using kilometers that is represented by km.
1 kilometer is about 1000 meters.

Measuring Heights – “How Tall?”
“How Tall?” is about measuring how high or tall something or someone is, like a tree or a person. We use units of measurement, like meters or feet, to find out the height from the ground to the top of the object or person.
Story Time: How tall we are?
Once upon a time in a park, there were boxes of flowers piled up high, forming a huge tower.

- All the kids gathered around to see how tall they were compared to the tower.
- Rajat stood next to the tower and found out he was 4 boxes tall.
Rajat is 4 boxes tall - Richa then stood beside Rajat and discovered she was 5 boxes tall.
Richa is 5 boxes tall - Finally, Disha joined them and realized she was 3 boxes tall.
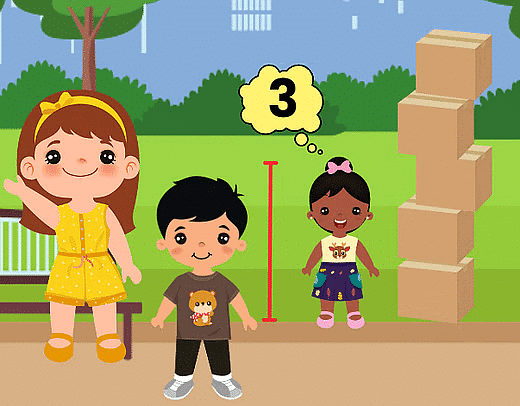 Disha is 3 boxes tall
Disha is 3 boxes tall - The kids were amazed to see how the tower helped them understand their heights in a fun way.
- They learned that comparing our height to something else, like a tower or a tree, can show us how high or tall we are.
Height is usually measured in meters.
1 m = 100 cm
Let’s Practice

Question: Look at the picture of the flower below. Can you guess the height of the flower with the help of the ruler given: View Answer
View Answer

Question: Upon looking at the following image, can you tell which one of the following kid is taller? View Answer
View Answer
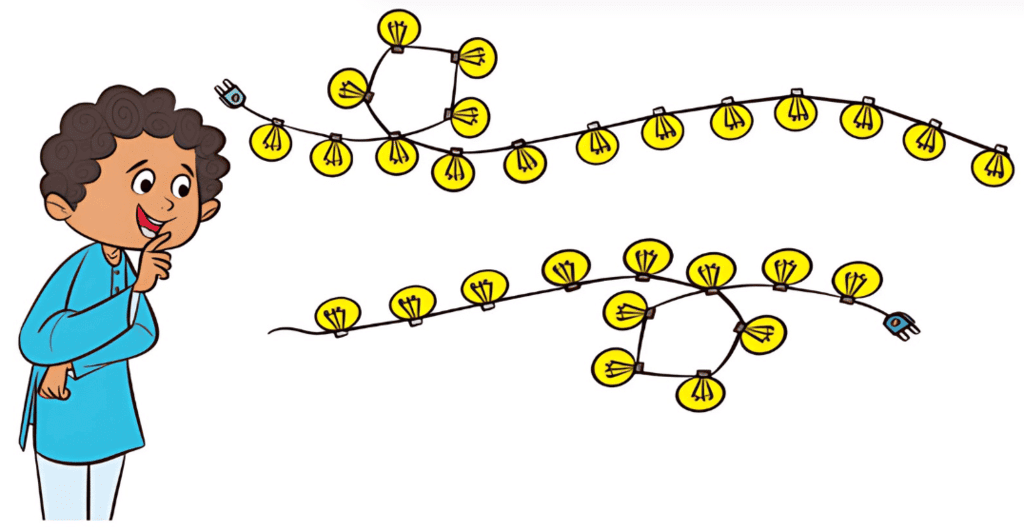
Question: Look at the strings and help Arjun choose the longest one. How did you find out? Discuss. View Answer
View Answer
In Summary, Measurement helps us find out how long, heavy, or full something is. We use units like centimeters (cm), meters (m) and kilometers (km) to measure lengths. Always remember that:
- 1 m = 100 cm
- 1 km = 1000 m

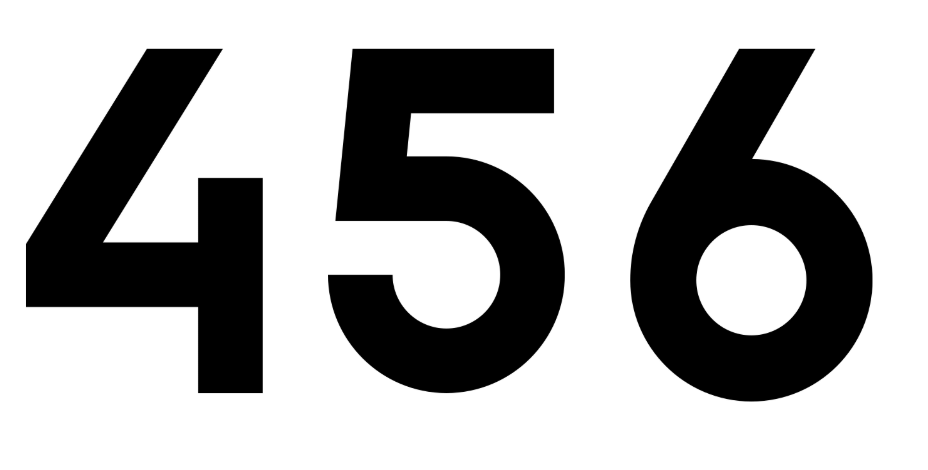




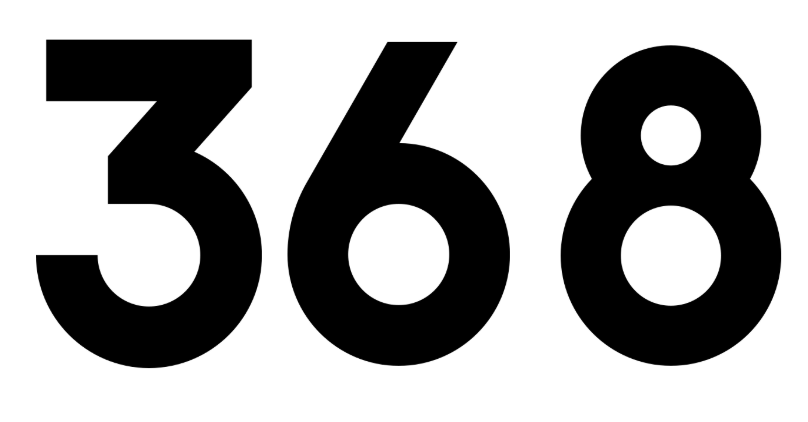


























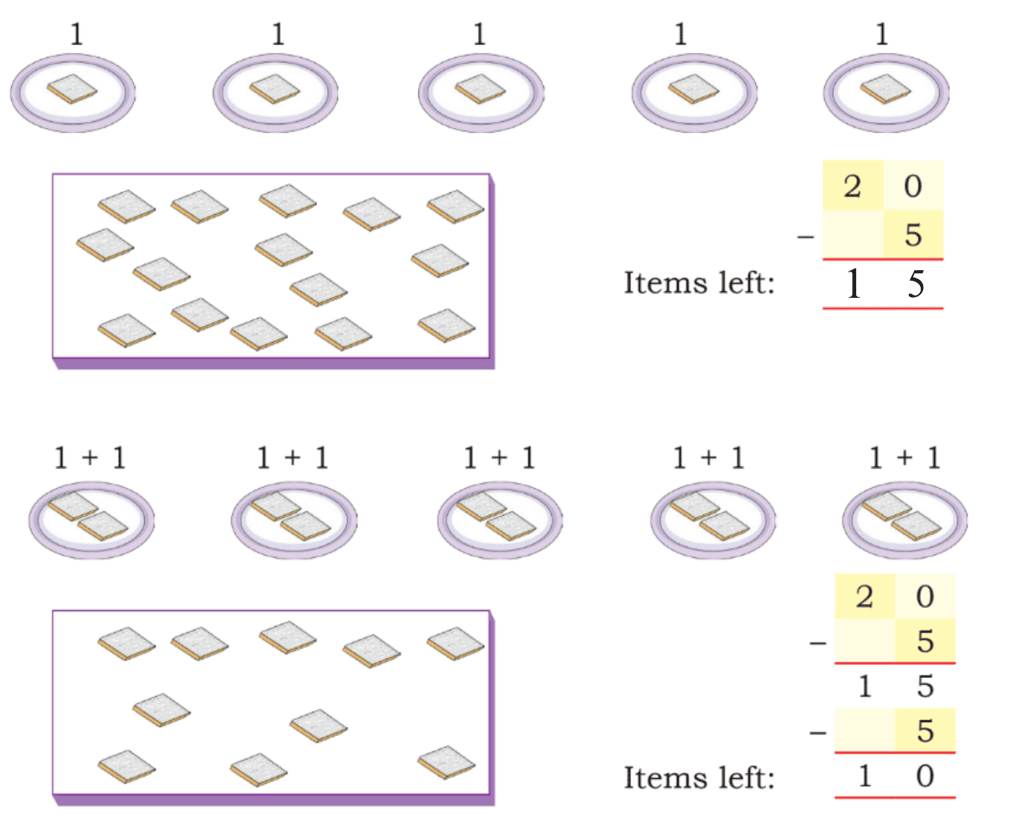
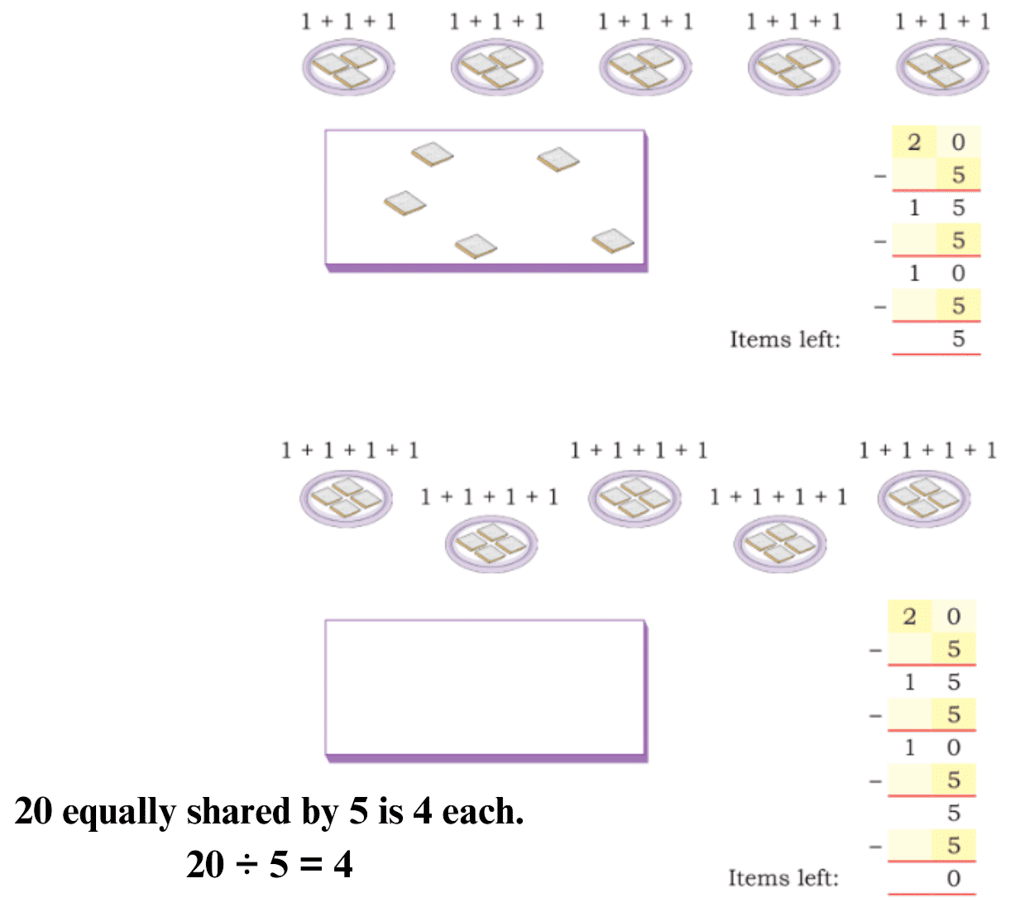












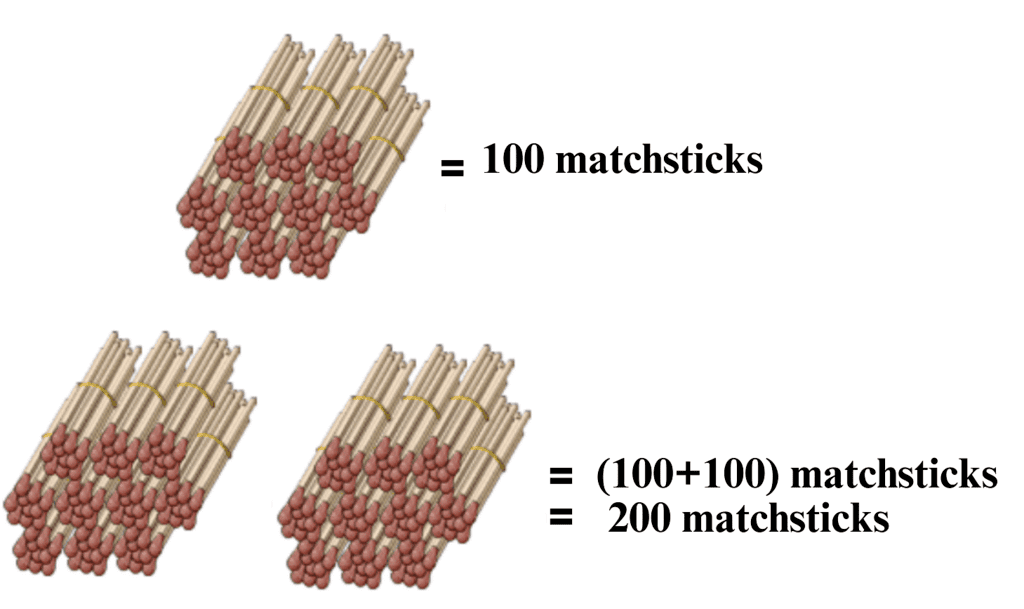
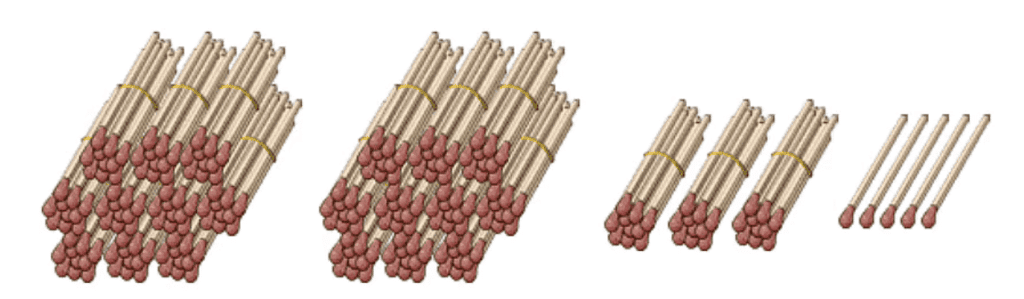
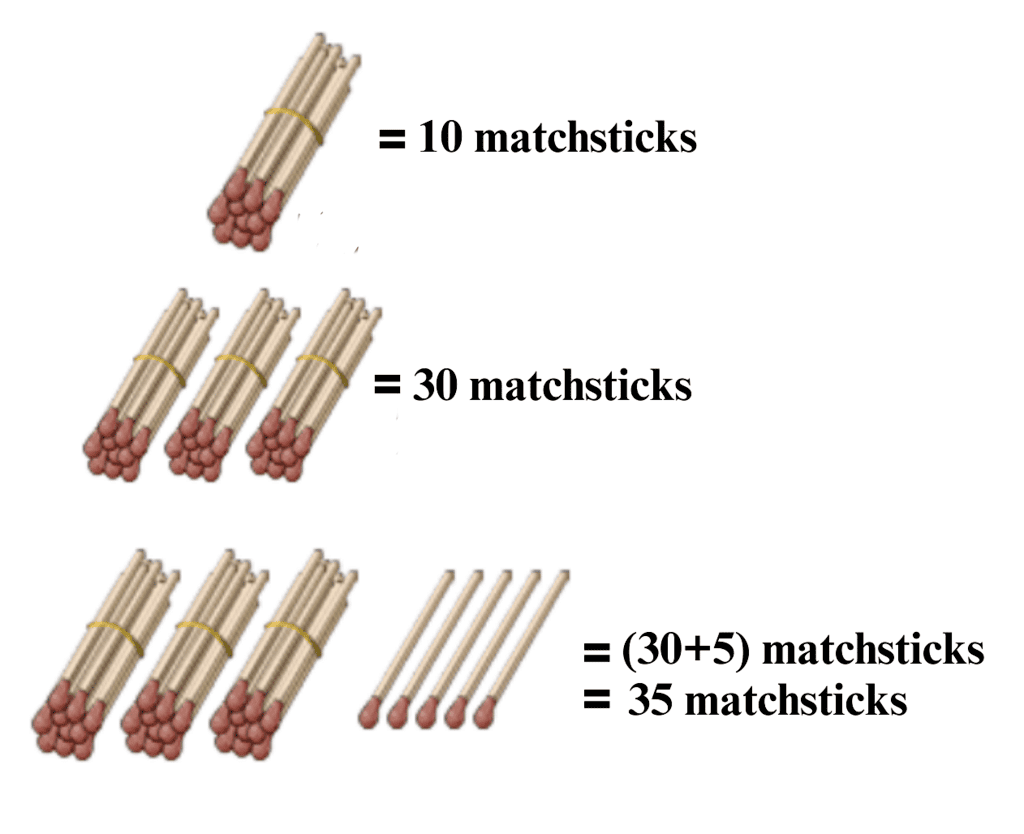







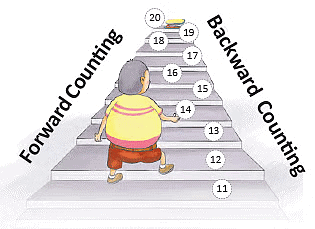
 The number 13 is to the left of 14. So, 13 < 14. The number 14 is to the right of 13. So, 14 > 13. Every number is equal to itself. 14 = 14, 15 = 15, 16 = 16, etc.
The number 13 is to the left of 14. So, 13 < 14. The number 14 is to the right of 13. So, 14 > 13. Every number is equal to itself. 14 = 14, 15 = 15, 16 = 16, etc.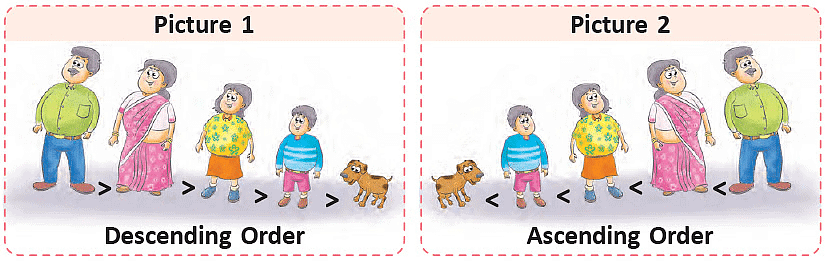


 Rectangle
Rectangle Square
Square Triangle
Triangle Circle
Circle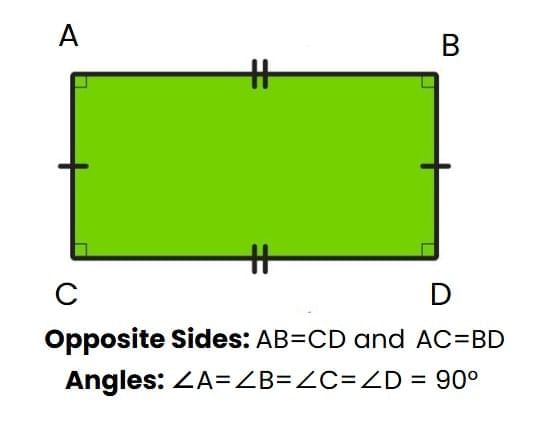
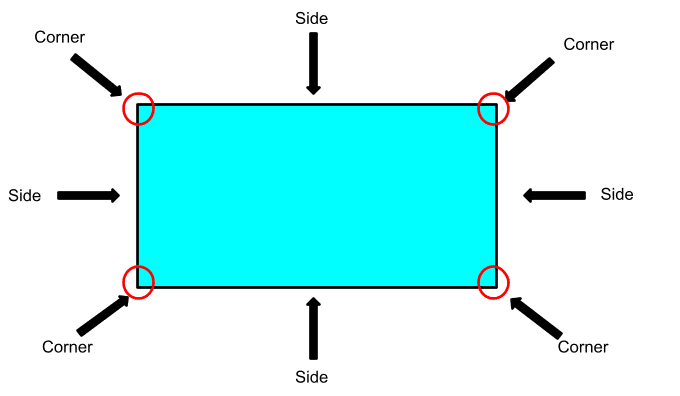

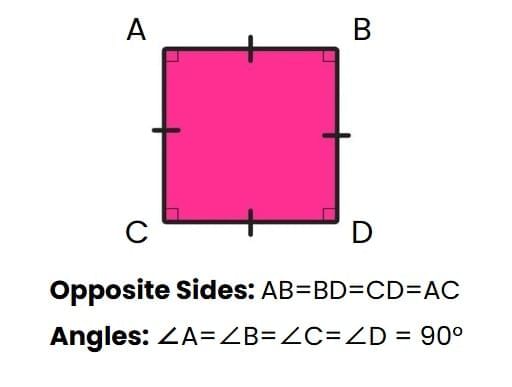
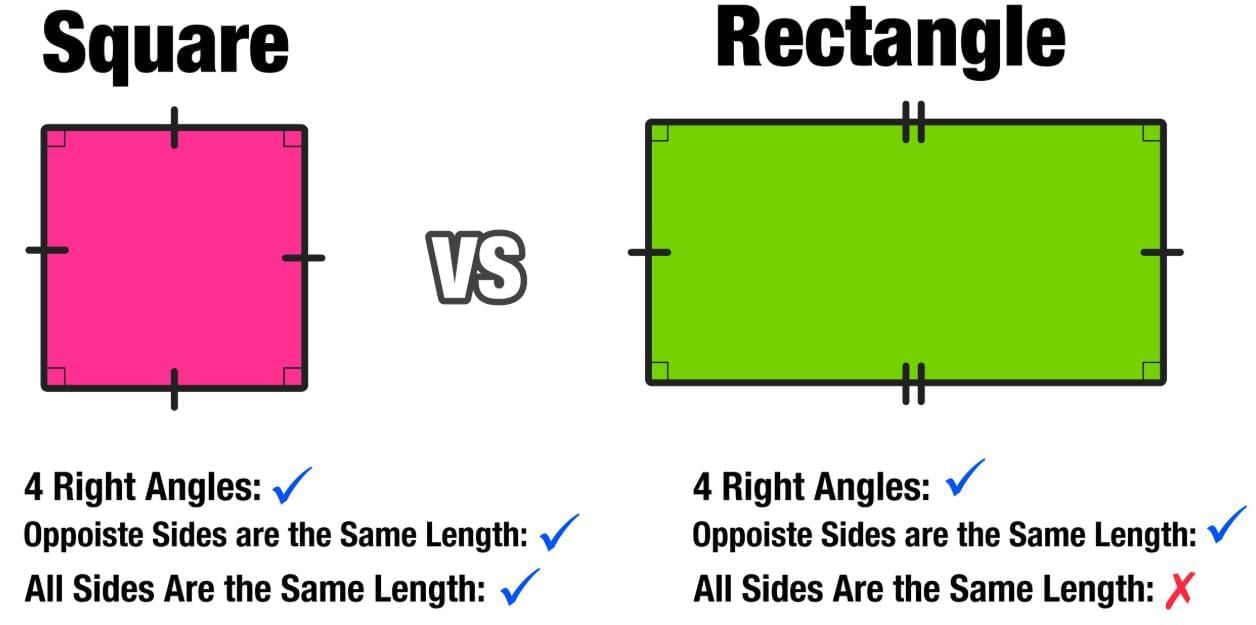
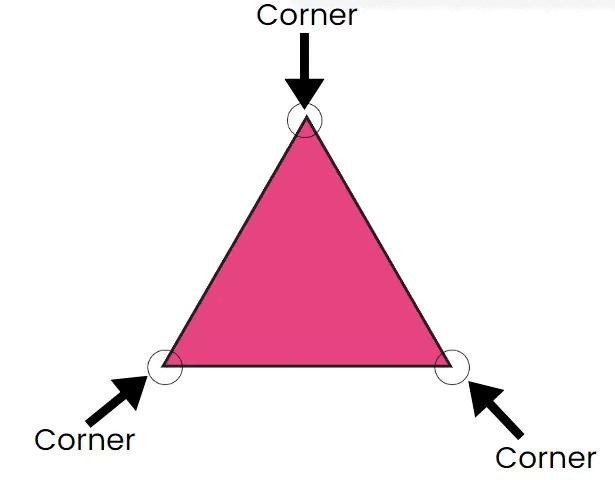
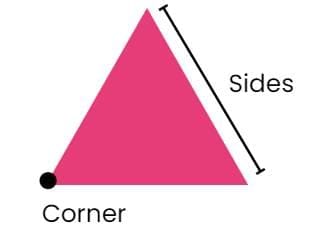

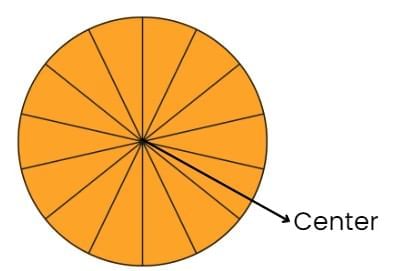
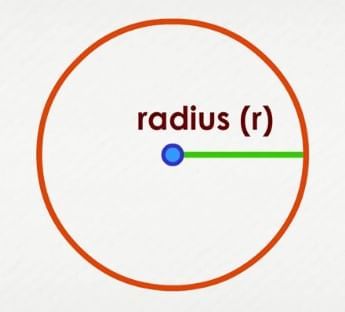
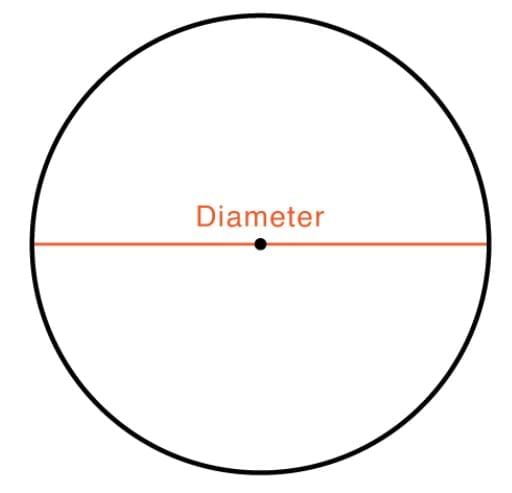
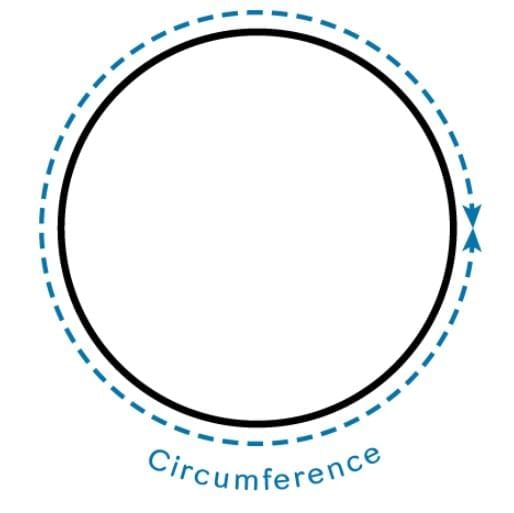













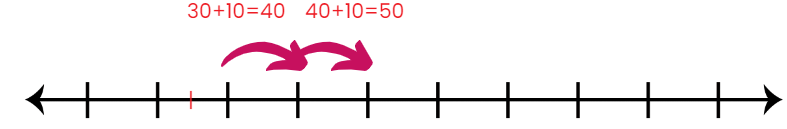
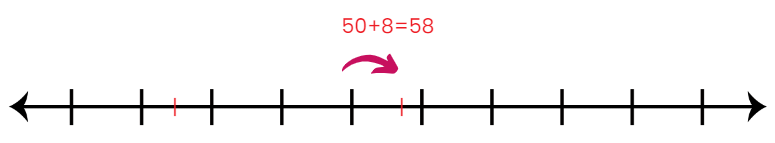



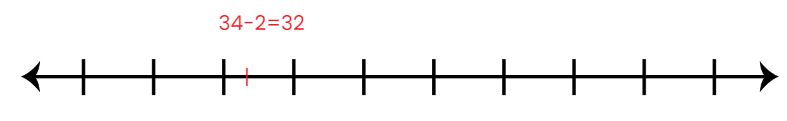




















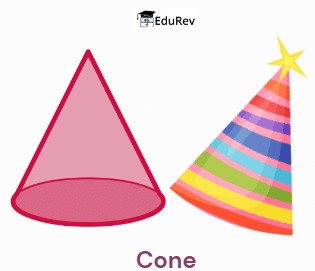
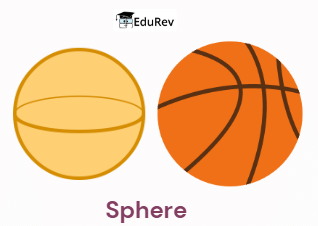
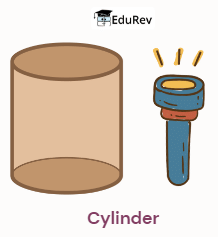

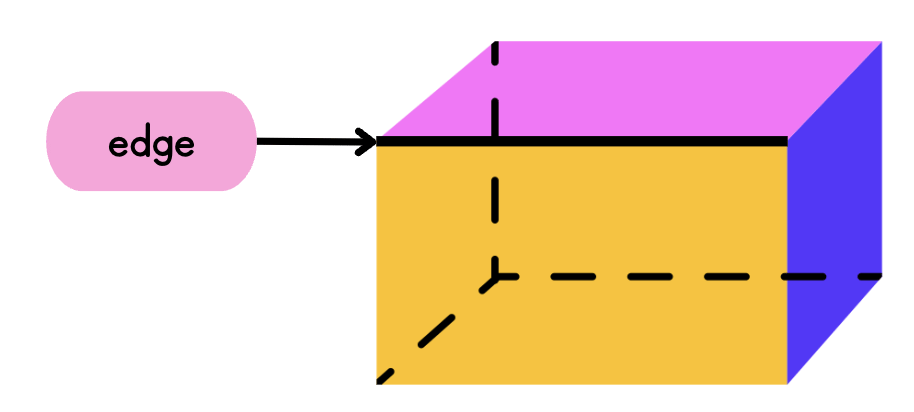
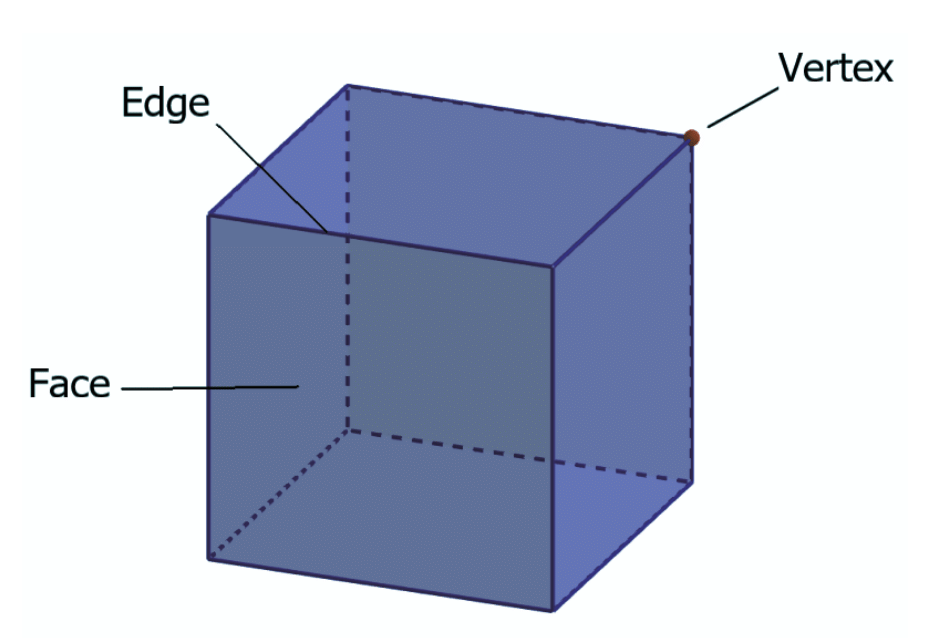
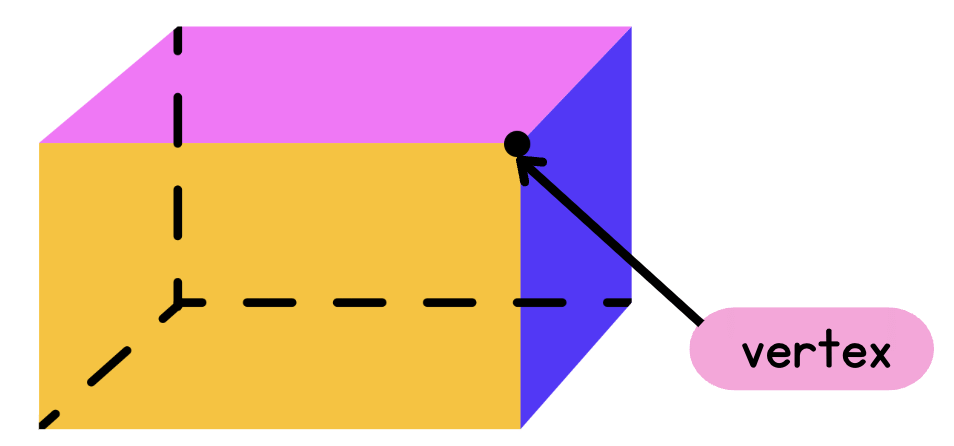 Now we will study how shapes differ from each other.
Now we will study how shapes differ from each other.









 Ayushi: A-Y-U-S-H-I = 6 letters
Ayushi: A-Y-U-S-H-I = 6 letters

 S-E-V-E-N = 5 letters
S-E-V-E-N = 5 letters

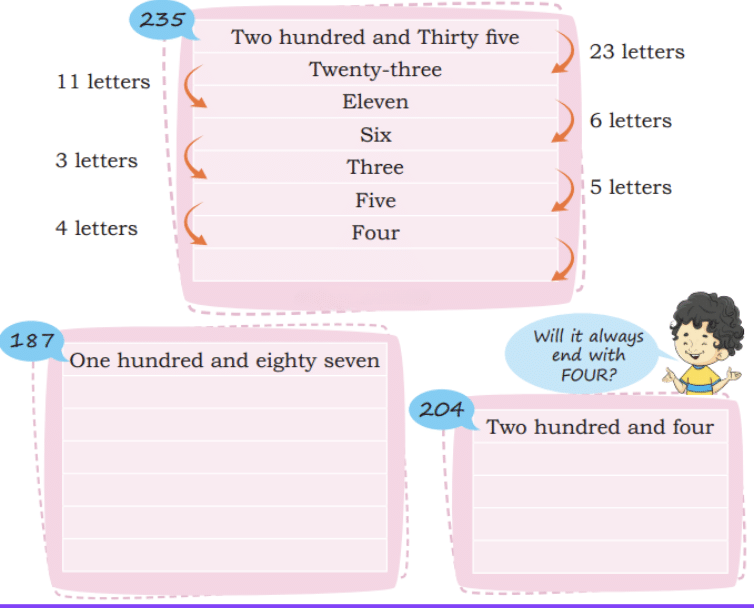
 “Eighty-Nine” = 10 letters
“Eighty-Nine” = 10 letters “Ninety” = 6 letters
“Ninety” = 6 letters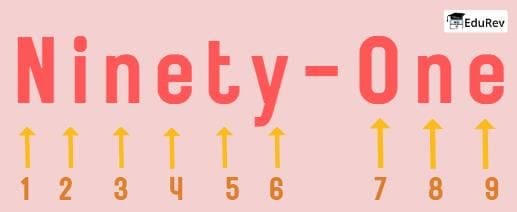 “Ninety-One” = 9 letters
“Ninety-One” = 9 letters