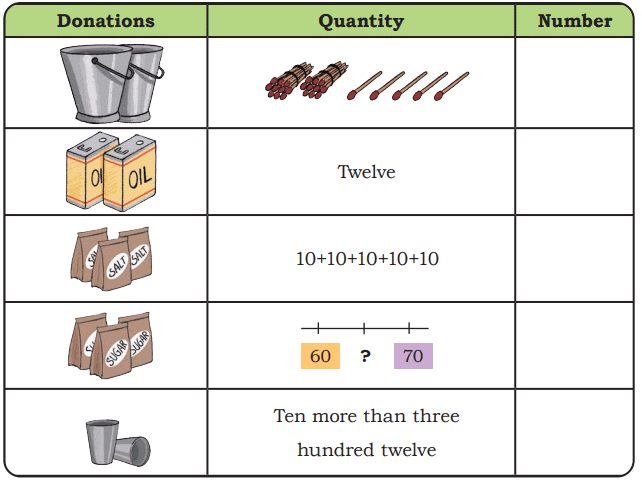
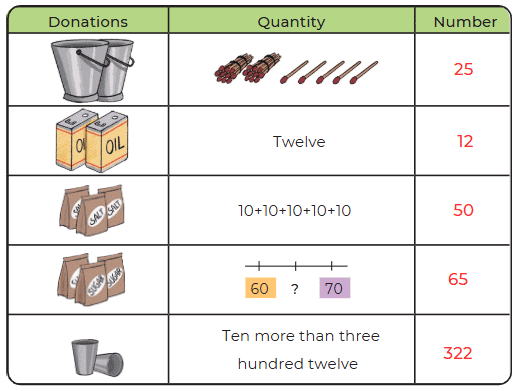
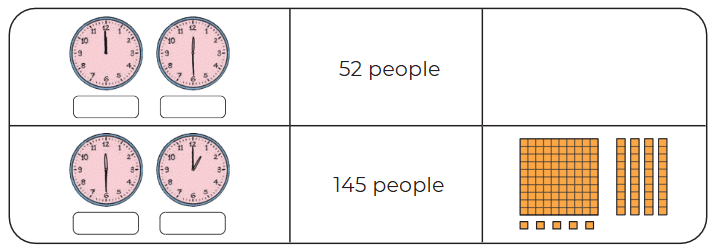
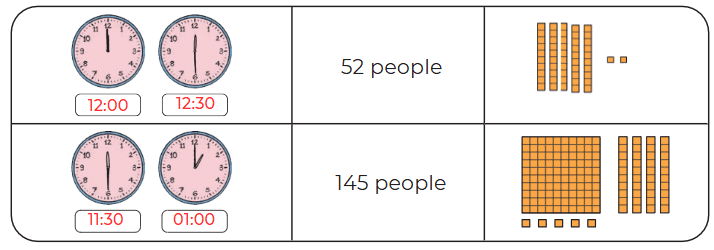
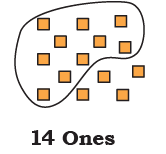
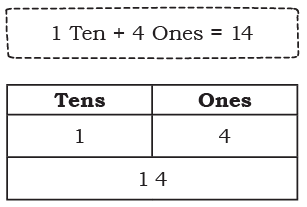
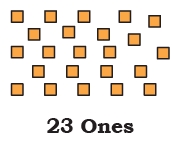
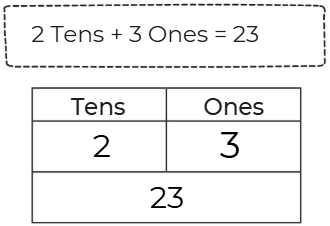
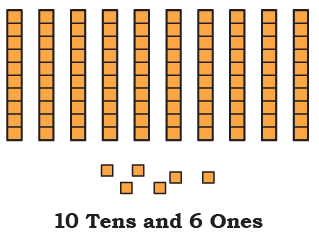
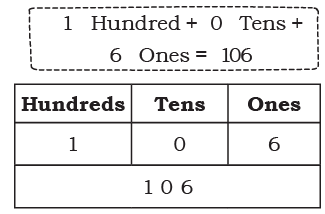
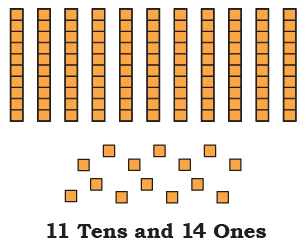
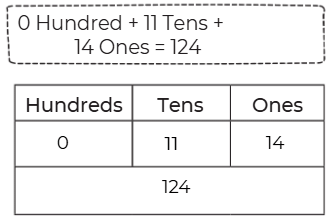
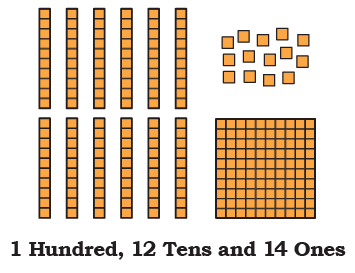
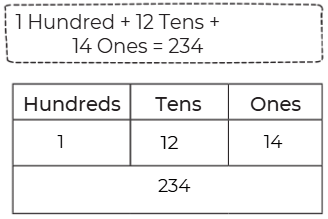
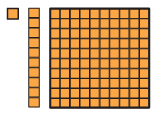
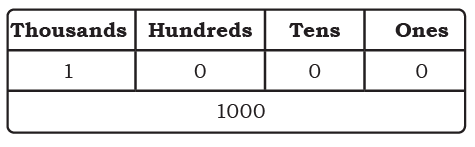
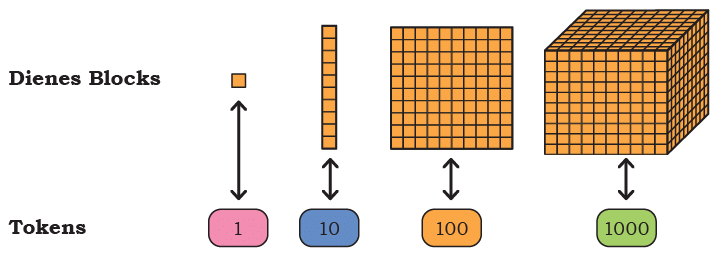
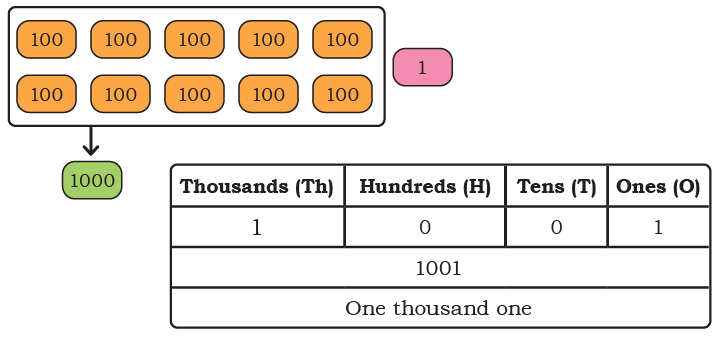
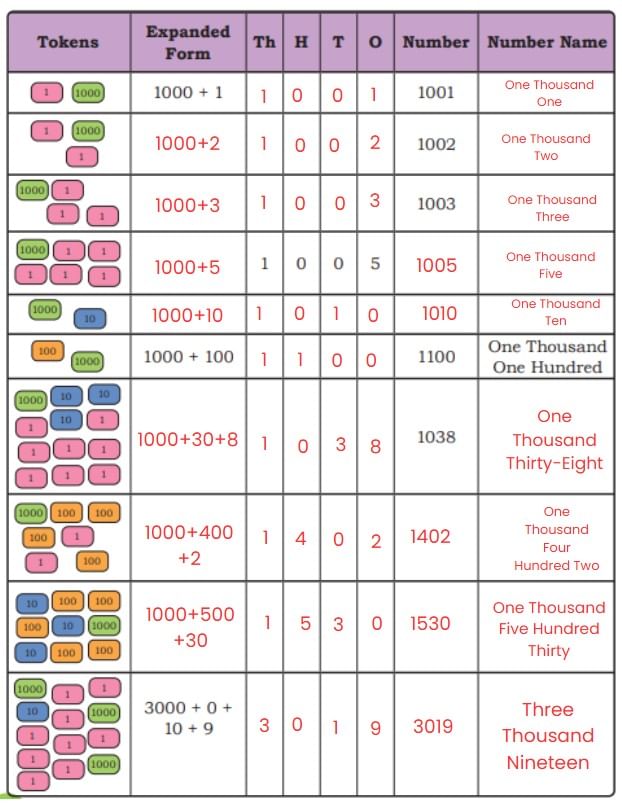
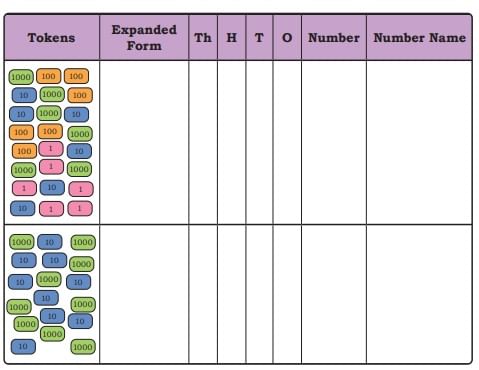
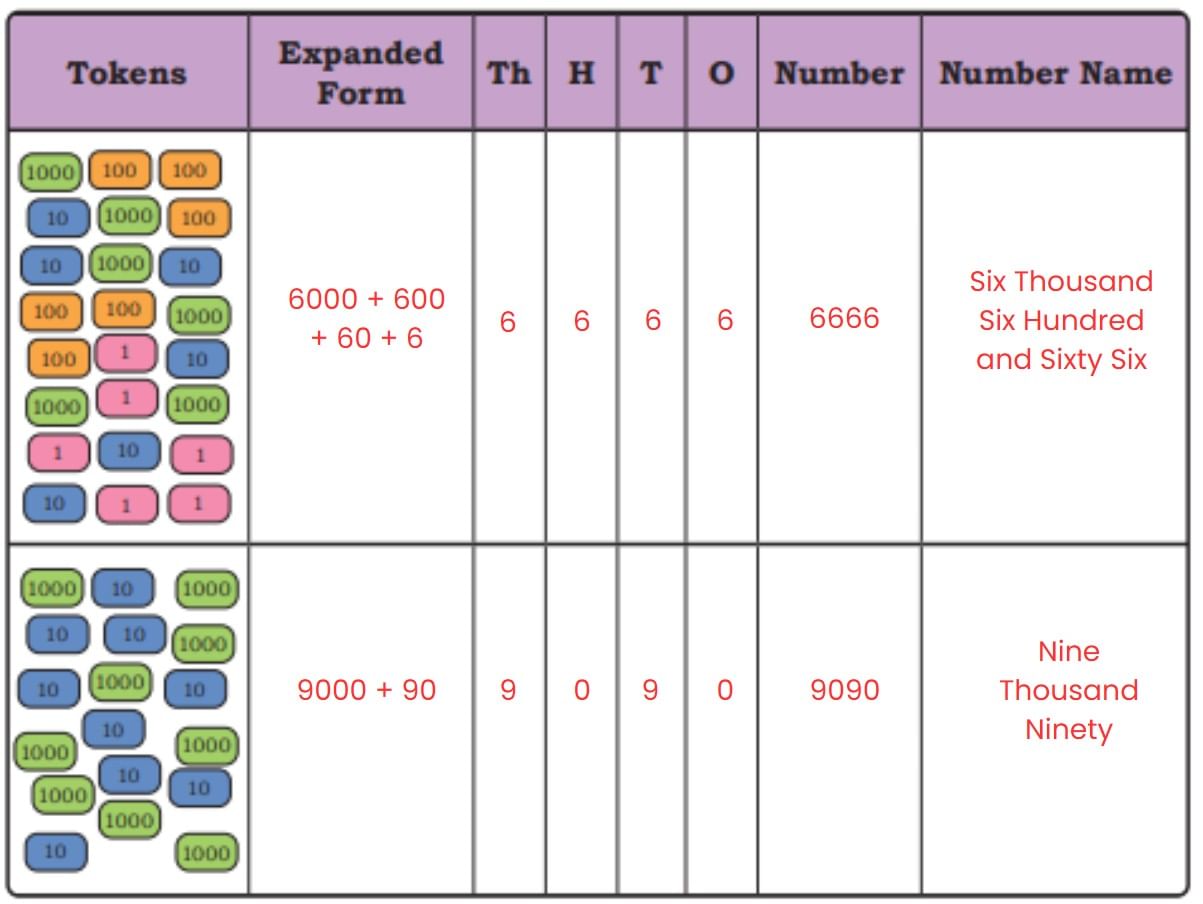
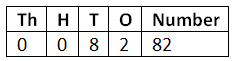
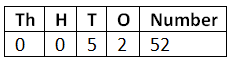
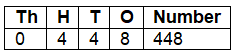
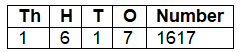
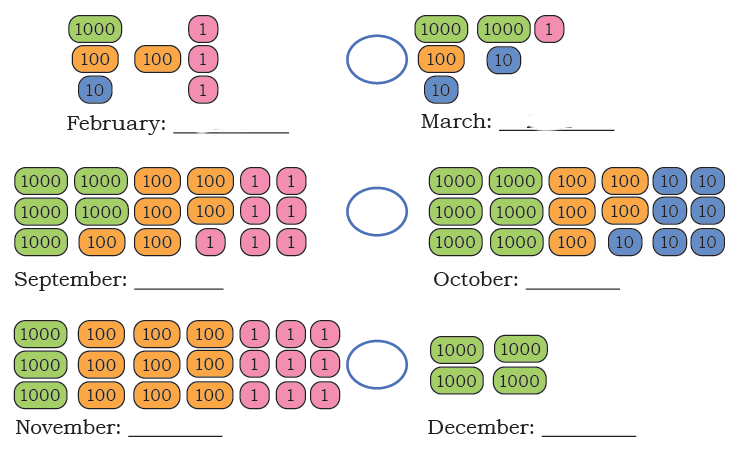
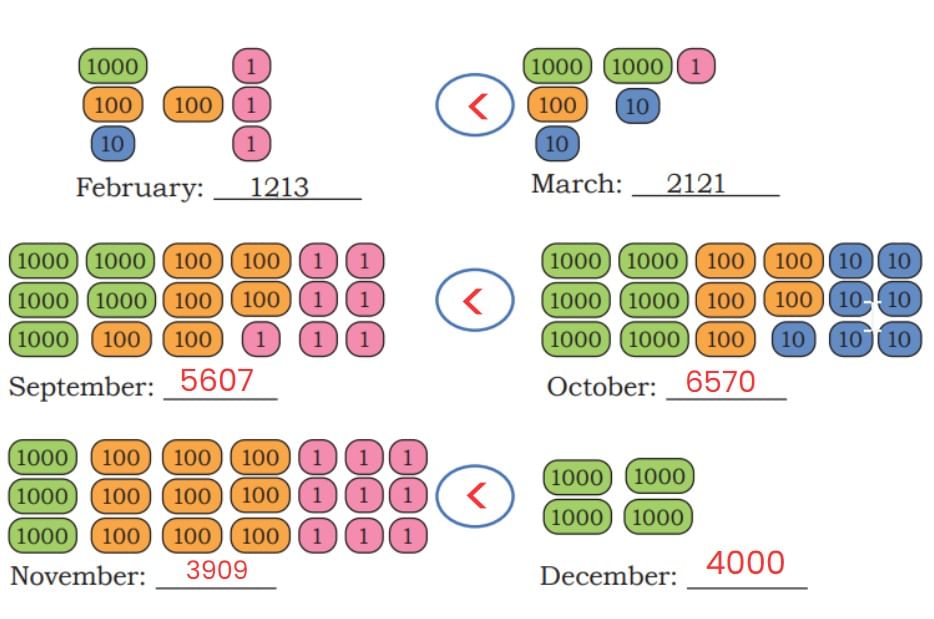
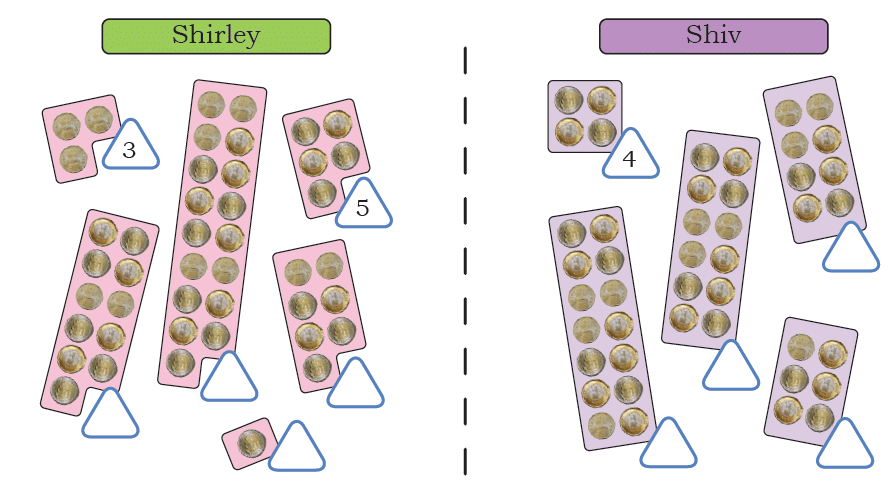
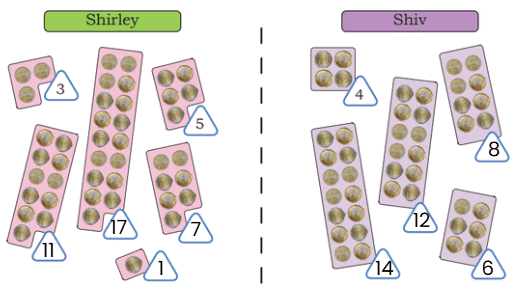
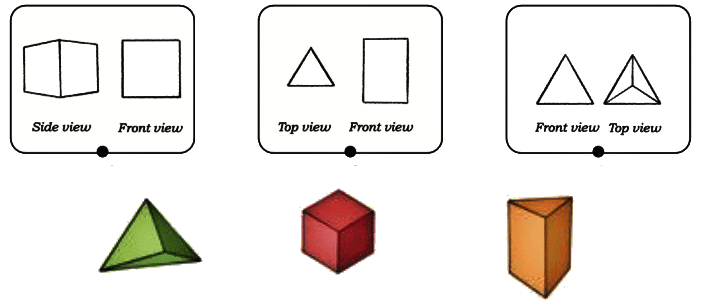
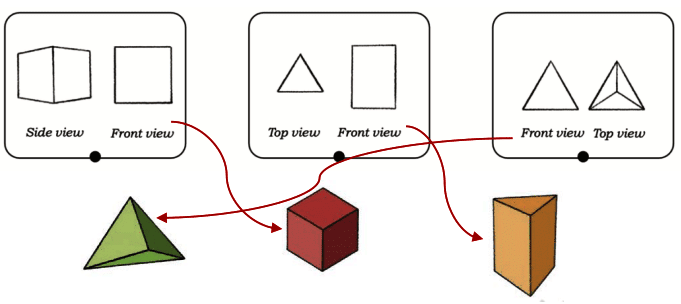
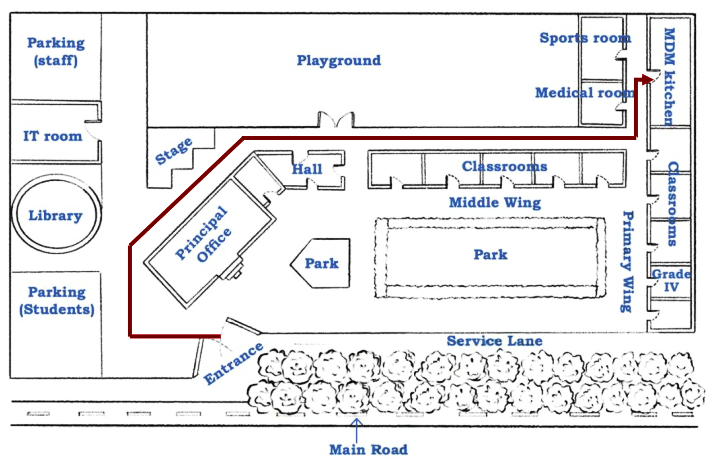
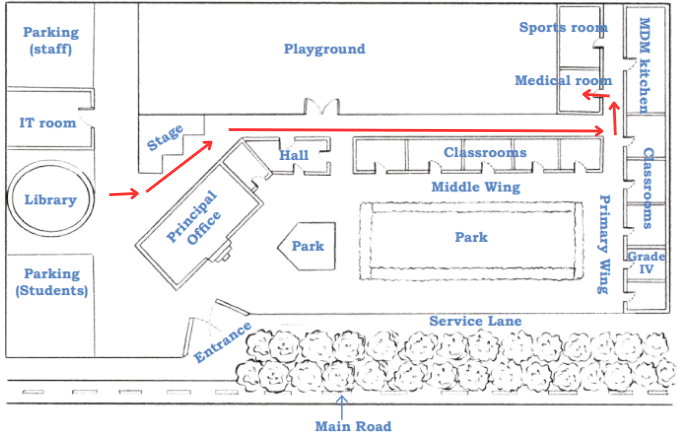
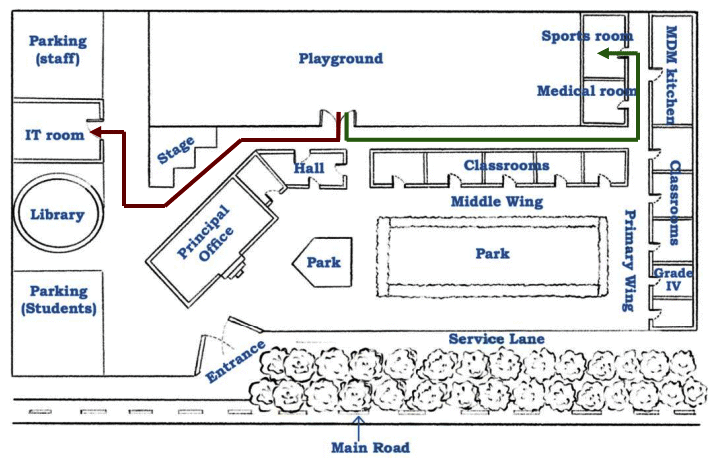
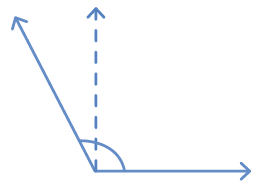
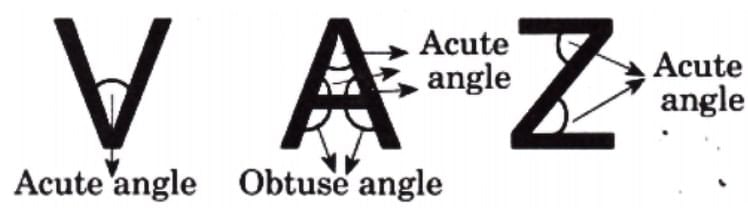
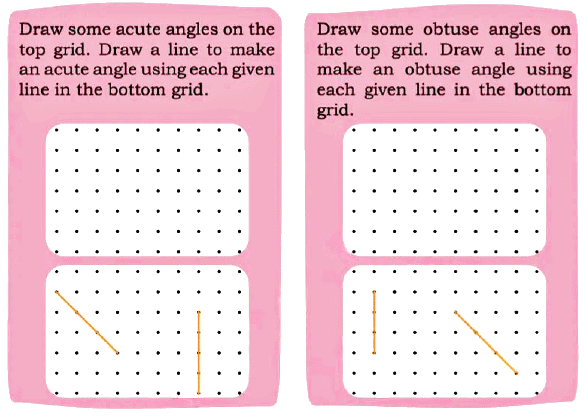
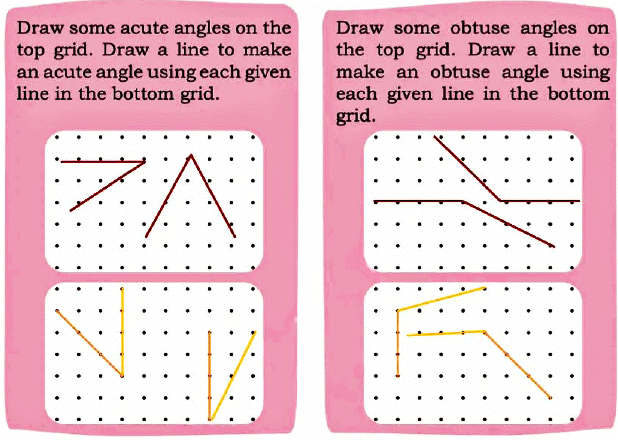
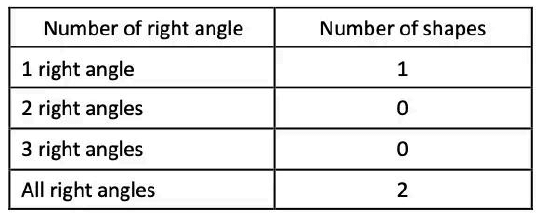
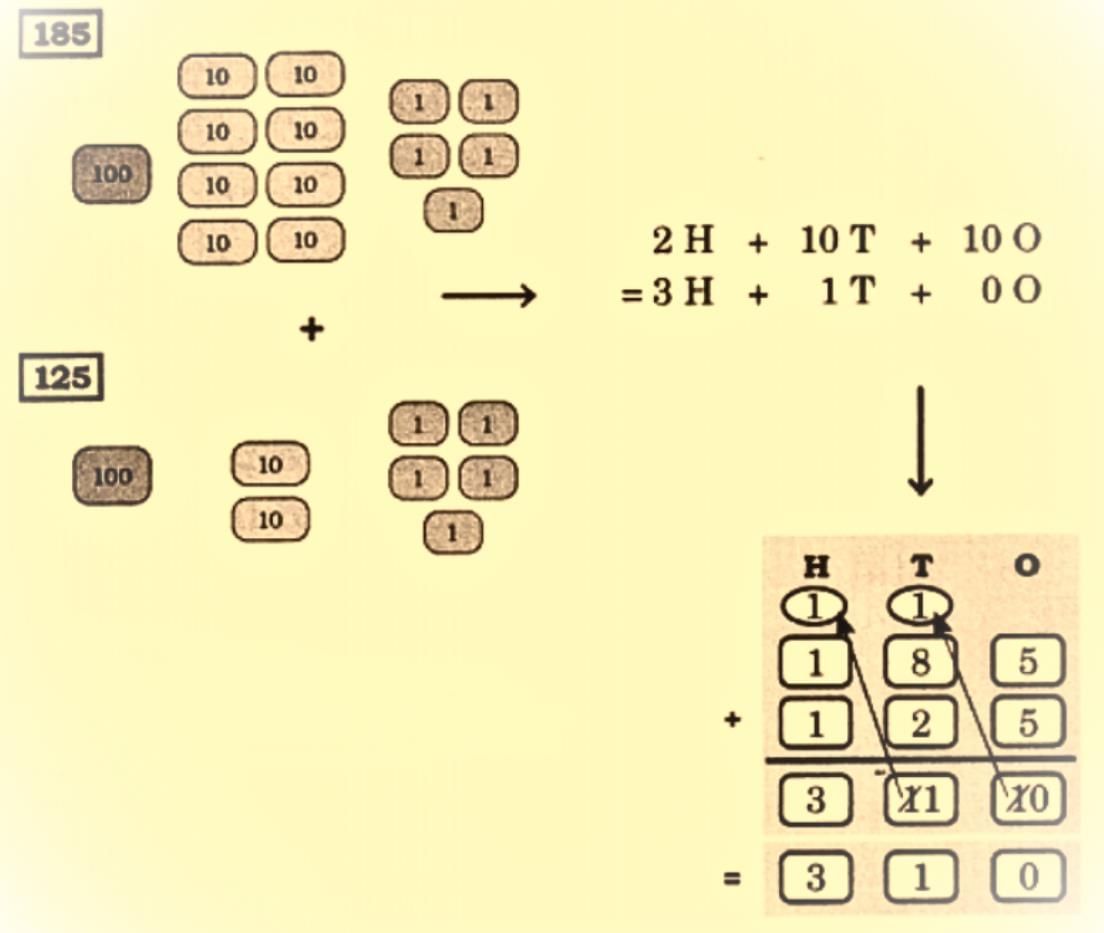
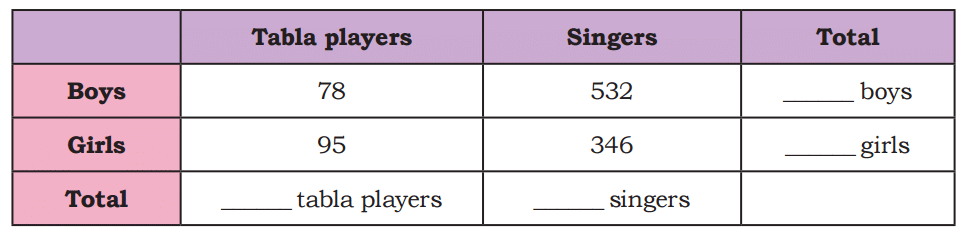
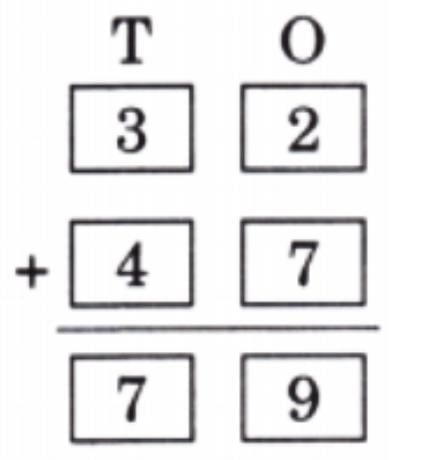
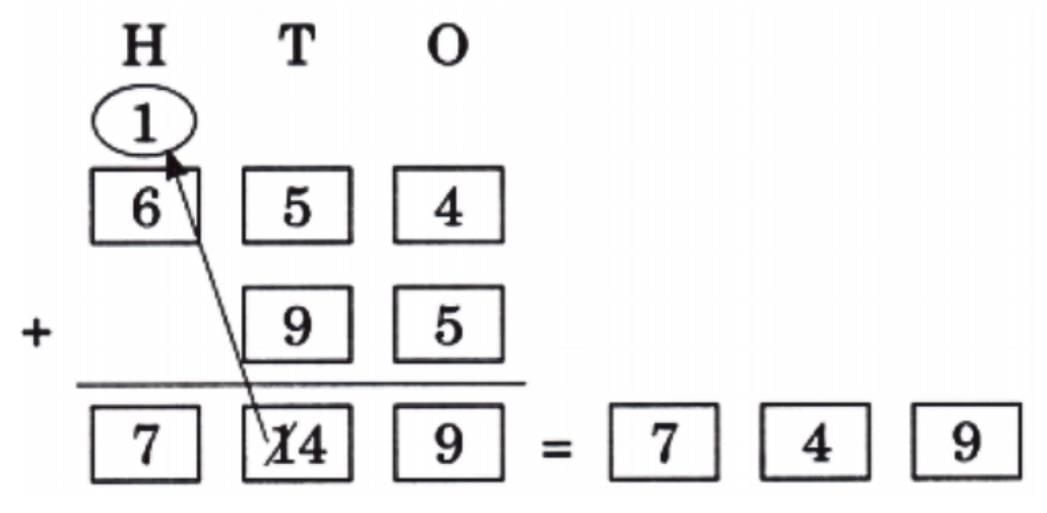
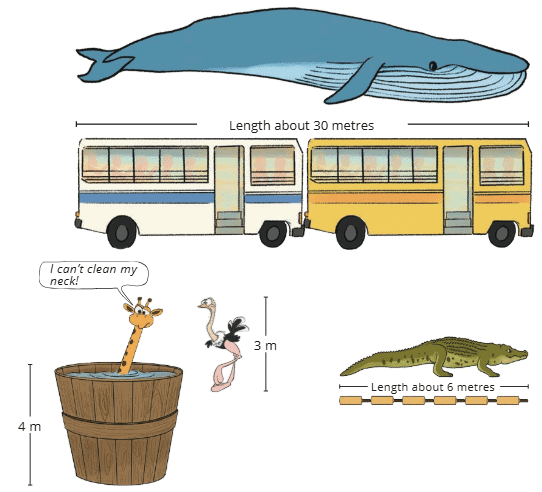
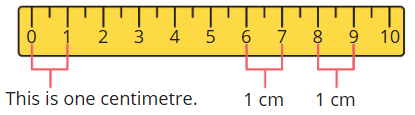
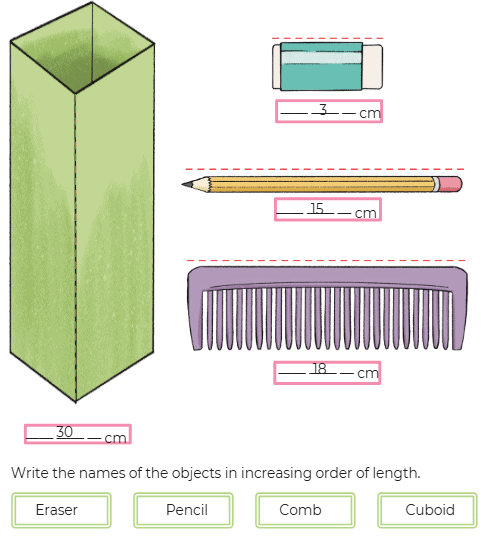
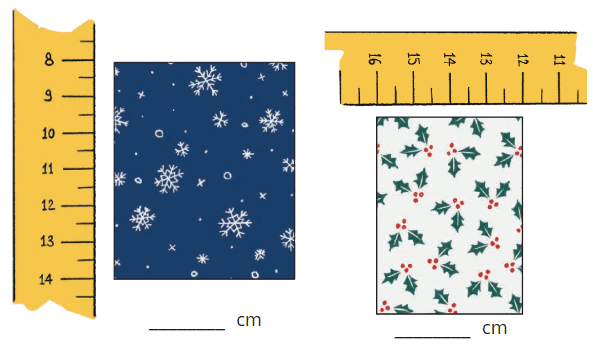
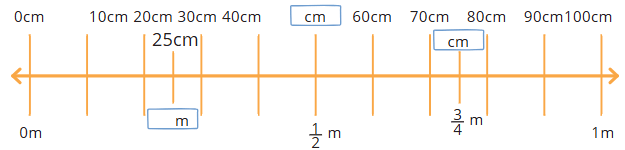
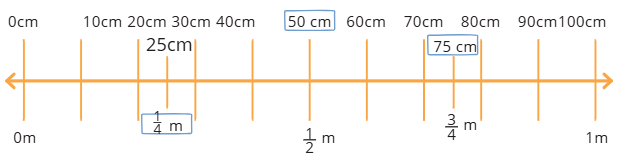
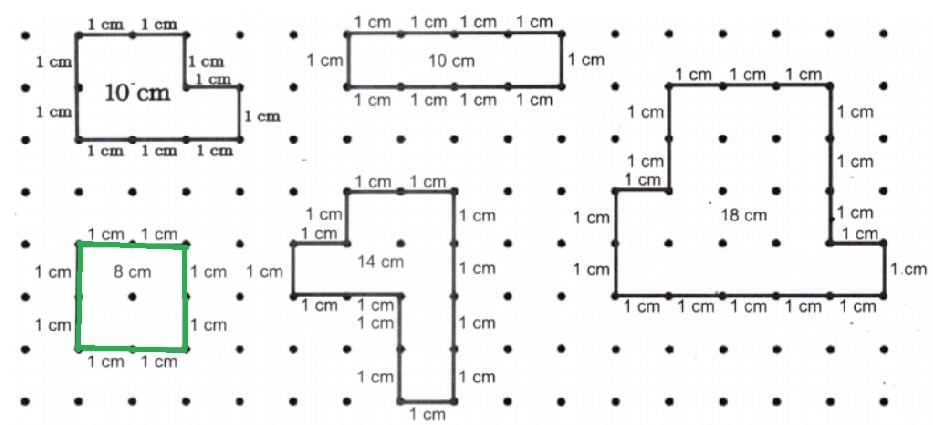
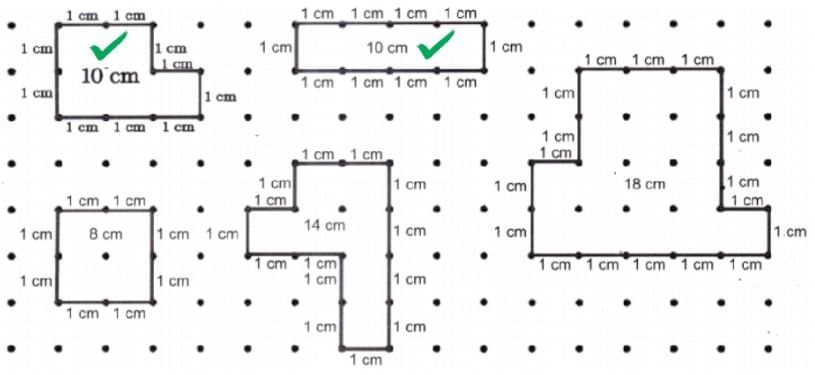
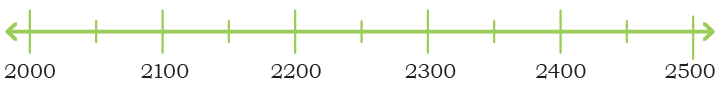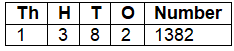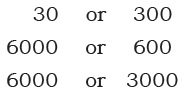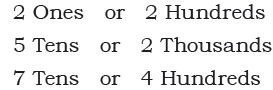Page 128
Animal Jumps
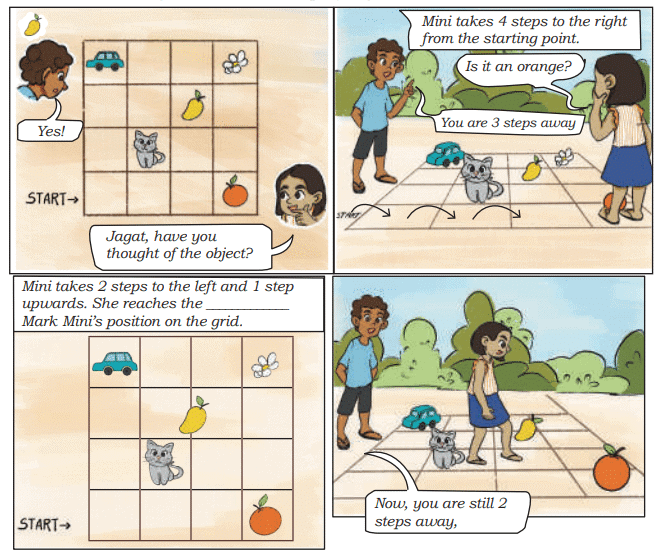
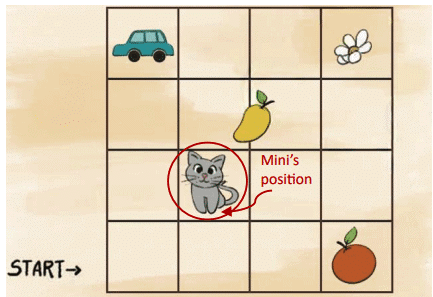
Fill in the blank spaces with the appropriate numbers. Find how many jumps the animal needs to take to reach its food.
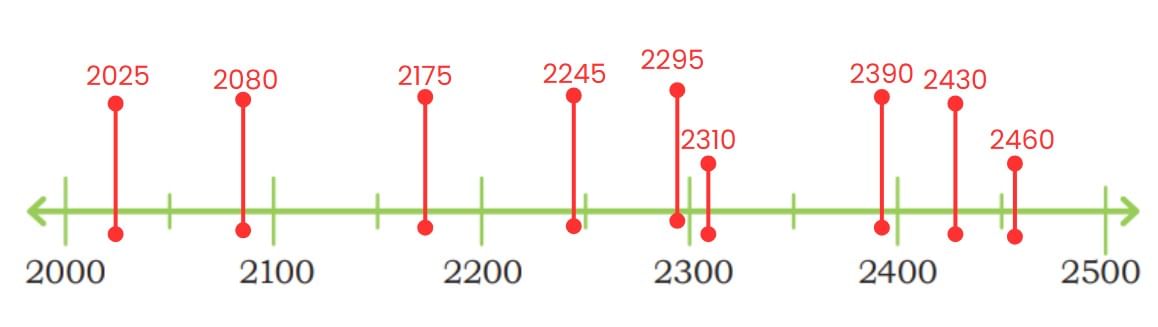
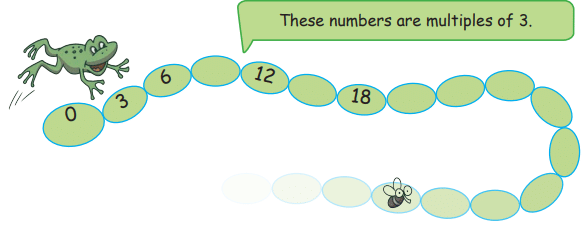
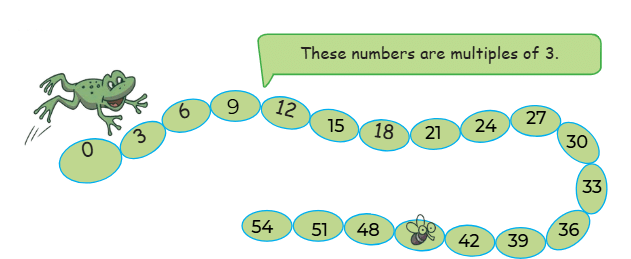
Q1: The frog jumps 3 steps at a time. Which numbers will the frog touch? Will it touch 67?
Ans:
- The frog will only touch numbers that are multiples of 3.
- Since 67 is not a multiple of 3, the frog will not touch 67.
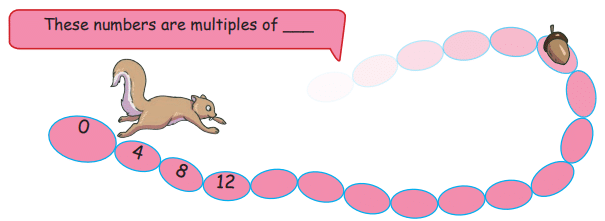
Q2: The squirrel jumps 4 steps at a time. Which numbers will the squirrel touch? How many times should the squirrel jump to reach 60?
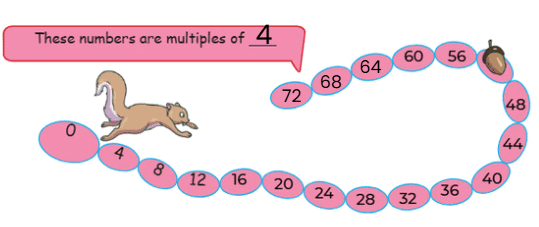
Ans:
- Numbers: Multiples of 4 (4, 8, 12, …, 60, 64, …).
- 60 ÷ 4 = 15 jumps.
Ans: Squirrel touches multiples of 4; 15 jumps to reach 60.
Page 129
Animal JumpsQ3: The rabbit jumps 6 steps at a time.
Which numbers will the rabbit touch?
What is the smallest 3-digit number on which the rabbit will land?
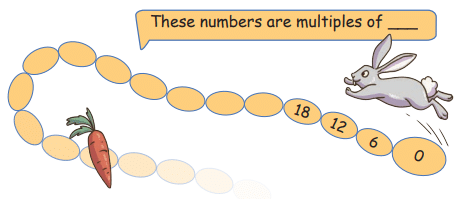
How many times did the rabbit jump to reach this number?
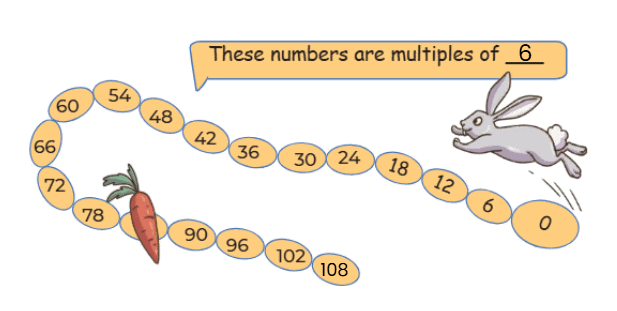
Ans:
- Numbers: Multiples of 6 (6, 12, 18, …, 96, 102, …).
- Smallest 3-digit number: 102 (first multiple of 6 ≥ 100).
- 102 ÷ 6 = 17 jumps.
Ans: Multiples of 6; smallest 3-digit number is 102; 17 jumps.


Q4: The kangaroo jumps 8 steps at a time. Which numbers will the kangaroo touch? Are there numbers that both the rabbit and the kangaroo will touch?Are there numbers that both the rabbit and the kangaroo will touch?
Ans:
- Numbers: Multiples of 8 (8, 16, 24, …, 96, 104, …).
- Common numbers: Common multiples of 6 and 8 (LCM = 24). E.g., 24, 48, 72, …
Ans: Multiples of 8; yes, rabbit and kangaroo touch numbers like 24, 48, 72.

Q5: To reach 48, how many times did the rabbit jump? How many times did the kangaroo jump to reach the same number?
What did you observe?
Ans: Since the rabbit jumped 6 steps at a time, 6 steps × 8 = 48. So, the rabbit jumped 8 times to reach 48.
And the kangaroo jumped 8 steps at a time, 8 steps × 6 = 48. So, the kangaroo jumped 6 times to reach the number 48.
We observe that due to size, rabbit take shorter steps than kangaroo and so reach later than kangaroo.
Page 130
Animal Jumps
Q6: To reach 60, how many times did the frog jump? How many times did the rabbit jump to reach the same number? What do you observe?
Ans: Since a frog jumped 3 steps at a time and 3 steps × 20 = 60.
So, the frog jumped 20 times to reach the number 60.
And the rabbit jumped 6 steps at a time, 6 steps × 10 = 60.
So, the rabbit jumped 10 times to reach the number 60.
We observe that due to difference in jump size, frog has to take more steps to reach the number 60.
Common Multiples
Q1: Which numbers do both the frog and the squirrel touch? A few common multiples of 3 and 4 are _________________.
Ans:
- Frog: Multiples of 3 (3, 6, 9, 12, …).
- Squirrel: Multiples of 4 (4, 8, 12, …).
- Common multiples (LCM = 12): 12, 24, 36, …
12, 24, 36, …
Q2: Which numbers do both the rabbit and the kangaroo touch? A few common multiples of 6 and 8 are ___________________.
Ans:
- Rabbit: Multiples of 6 (6, 12, 18, 24, …).
- Kangaroo: Multiples of 8 (8, 16, 24, …).
- Common multiples (LCM = 24): 24, 48, 72, …
24, 48, 72, …
Q7: If the cat and the rat land on the same number, the cat will catch the rat. The cat is now on 6 and the rat on 12. When the cat jumps 3 steps forward, the rat jumps 2 steps forward. Will the cat catch the rat? If yes, at which number?
Ans:
- Cat: Starts at 6, jumps 3 steps (9, 12, 15, 18, 21, 24, …).
- Rat: Starts at 12, jumps 2 steps (14, 16, 18, 20, 22, 24, …).
- Common number: 24 (cat reaches 24 in 6 jumps, rat in 6 jumps).
Yes, cat catches rat at 24.
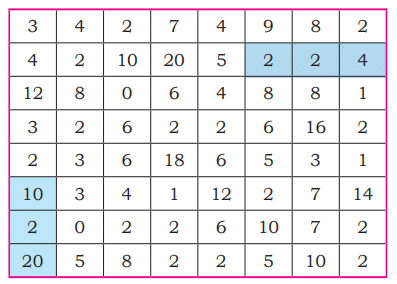
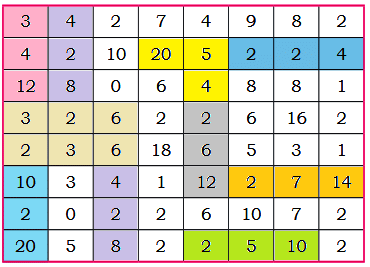
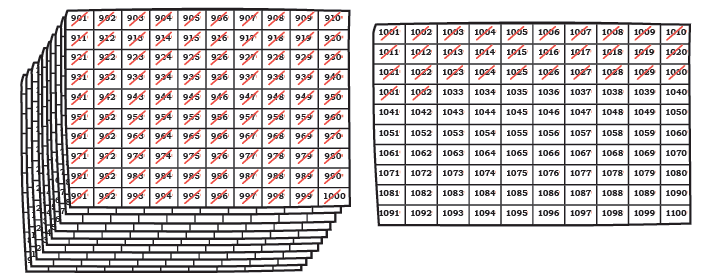
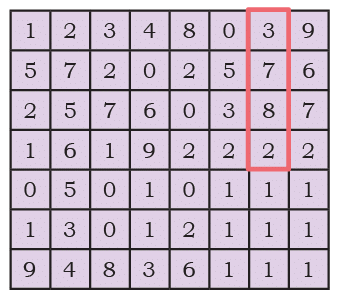
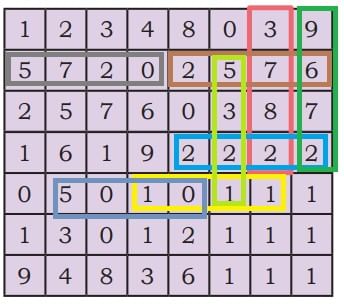
Q8: Find multiplication and division sentences in the grid. Shade the sentences. How many can you find?Two examples are done for you.
Ans:
We can make 15 such sentences.
Page 131
Gulabo’s Garden

Q1: Gulabo’s garden has lily flowers. Each lily flower has 3 petals. How many petals are there in 12 flowers? Show how you found your answer.
Gulabo will have 12 × 3 petals.
Petals in 10 lilies 10 × 3 petals = 30 petals
Petals in 2 lilies __________________
Petals in 12 lilies _________________
Ans: There are 36 petals in 12 flowers.
I found it by multiplying 12 flowers by 3 petals each: 12 × 3 = 36.
First, 10 lilies have 10 × 3 = 30 petals.
Then, 2 lilies have 2 × 3 = 6 petals.

Petals in 12 lilies = 12 × 3 = 36 petals
Adding them together, 30 + 6 = 36 petals.

Q2: In a hibiscus flower there are 5 petals. Gulabo counted all the petals and found them to be 80. How many flowers did she have?Gulabo has 80 ÷ 5 flowers.
5 petals is 1 flower.
10 petals are 2 flowers.
50 petals are 10 flowers.
Then, 80 petals are _______ flowers.
Ans:
- 80 ÷ 5 = 16 flowers.
- Method: 50 ÷ 5 = 10, 30 ÷ 5 = 6, 10 + 6 = 16.
16 flowers; 80 ÷ 5 = 16.
Page 132
Gulabo’s Garden

Q3: Gulabo plants some marigold saplings in a box as shown in the picture.
There are ______ saplings in each row.
There are ______ rows.
How many saplings has she planted?
How did you calculate it?
Mathematical Statement _________________
Ans: There are 11 saplings in each row.
There are 3 rows.
Gulabo has planted a total of 33 saplings in the box.
By using multiplication, we found the number of saplings.
Mathematical statement: There are 3 rows in the box, where the saplings planted are 11 times the number of rows.
Total saplings planted = 3 × 11 = 33

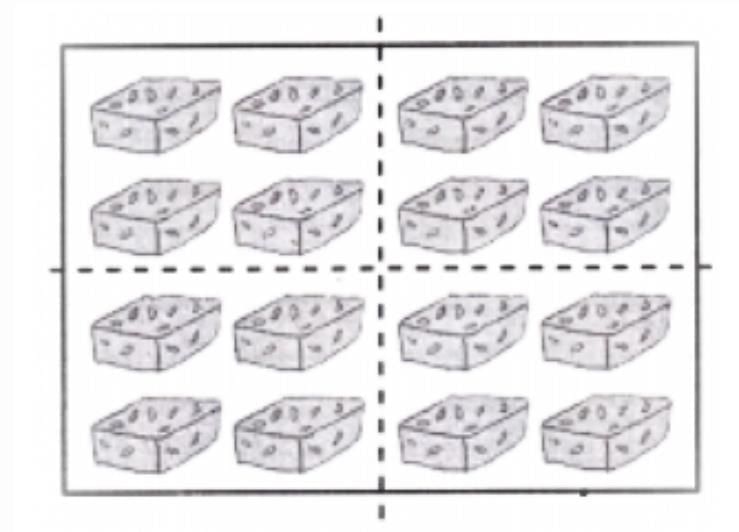
Q4: “Dailyfresh” supermarket has kept boxes of strawberries in a big tray.
How many boxes of strawberries does the supermarket have?
Show how you found them.There are _______ columns of strawberry boxes.
There are _______ boxes in each column.
There are _______ boxes in all.
Mathematical Statement _________________
Ans: There are 16 columns of strawberry boxes.
There are 6 boxes in each column.
There are 16 × 6 = 96 boxes in all.
Mathematical statement: The number of boxes of strawberry = Number of columns of strawberry boxes × number of boxes in each column = 16 × 6 boxes = 96 boxes
Q5: Radha runs a bakery shop. She bakes 18 cupcakes in one tray of the size shown below.
(a) Complete arranging the cupcakes in the two trays given below.

Ans: Radha has 18 cupcakes to arrange in two trays. The first tray already has 8 cupcakes.
- First tray: 8 cupcakes are already there.
- Cupcakes left = 18 – 8 = 10 cupcakes.
- Put the remaining 10 cupcakes in the second tray.
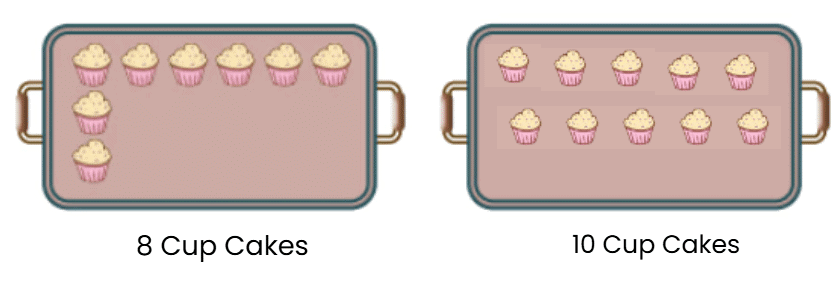
So, the arrangement is:
- First tray: 8 cupcakes.
- Second tray: 10 cupcakes.
(b) She can use two such trays in her oven at a time. How many cupcakes can she make in one attempt? _______
Ans: Number of cupcakes in a tray = 18
Number of cupcakes in two trays = 2 × 18 = 36
The number of cupcakes, she can make in one attempt = 36
(c) Today she has received a special order. She has made 108 cupcakes. How many trays has she baked?
Ans: Number of cupcakes in two trays = 36
Number of cupcakes in 4 trays = 2 × 36 = 72
Number of cupcakes in 6 trays = 3 × 36 = 108
So, the required number of trays = 6
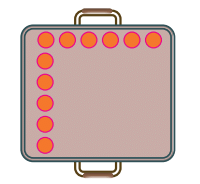
(d) She has another square baking tray. She can bake 36 mini cupcakes in such a tray. Complete the arrangement below.Number of columns: _______
Number of cupcakes in each column: _______
Multiplication statement _______
Ans: Number of columns = 6
Number of cupcakes in each column = 6
Multiplication statement: 6 × 6 = 36.
Q: Find different ways of arranging the following numbers of cupcakes in rows and columns in your notebook.
36, 8, 12, and 24
Ans:
- 36 cupcakes can also be arranged in a tray having 9 rows, and each row has 4 cupcakes.
- 8 cupcakes can be arranged in 4 columns, with 2 cupcakes in each column.
- 12 cupcakes can be arranged in 2 rows, with each row having 6 cupcakes.
- 24 cupcakes can be arranged in 6 columns, and each column has 4 cupcakes.
Page 134
The Doubling Magic
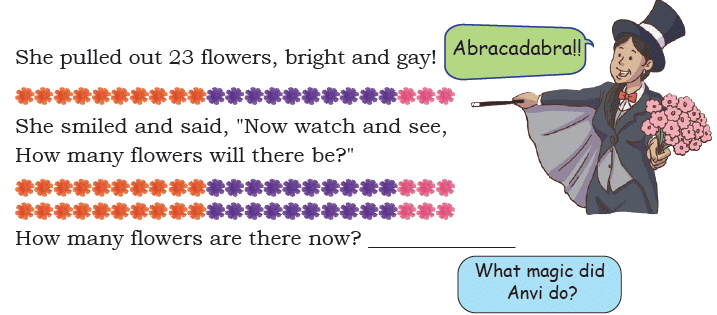
Magician Anvi came one day,
To Gulabo’s house, ready to play.
From her coat, with a grand display,

(a) Double of 32 =_____
Ans: 32 × 2 = 64
(b) Double of 14 =_____
Ans: 14 × 2 = 28
(c) Double of 26 =_____
Ans: 26 × 2 = 52
(d) Double of 17 =_____
Ans: 17 × 2 = 34
(e) Double of 39 =_____
Ans: 39 × 2 = 78
(f) Double of 45 =_____
Ans: 45 × 2 = 90
1. Guess what will be the ones digit of the following numbers when doubled.
Write the ones digit in the space provided.
(a) 28 ______
Ans: 28 × 2 = 56; ones digit: 6
(b) 56 ______
Ans: 56 × 2 = 112; ones digit: 2
(c) 45 ______
Ans: 45 × 2 = 90; ones digit: 0
(d) 17 ______
Ans: 17 × 2 = 34; ones digit: 4
2. Give examples of numbers that when doubled give the following digits in the ones place.
(a) 0 _______
Ans: 5, 10, 15 (e.g., 5 × 2 = 10)
(b) 2 _______
Ans: 1, 6, 11 (e.g., 1 × 2 = 2)
(c) 4 _______
Ans: 2, 7, 12 (e.g., 2 × 2 = 4)
(d) 6 _______
Ans: 3, 8, 13 (e.g., 3 × 2 = 6)
(e) 8 _______
Ans: 4, 9, 14 (e.g., 4 × 2 = 8)
Can we get 3, 5, 7, 9 as the ones digit after doubling?
Ans: No; doubling gives even ones digits (0, 2, 4, 6, 8).
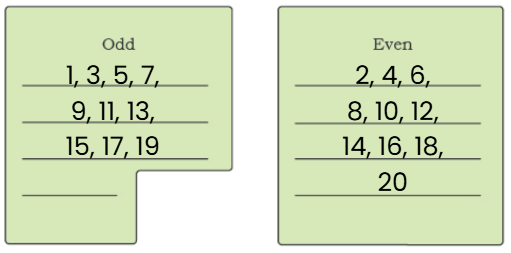
What do we notice about the numbers that we get after doubling? Even or Odd?
Observation: Doubled numbers are even.
Page 135 & 136
Multiplication Chart
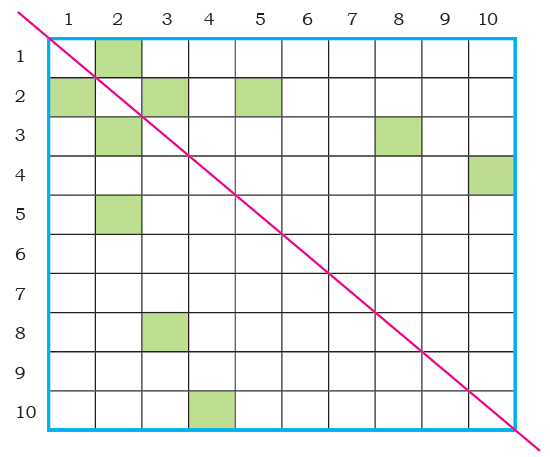
Fill each square in the chart by multiplying the row number by the column number.
What do you notice about the numbers shaded in green? Why is this happening?
Ans: We notice that the numbers shaded in green, show that when we multiply any two numbers, the order does not matter. For example, 1 × 2 = 2 = 2 × 1, 2 × 3 = 6 = 3 × 2, 5 × 2 = 10 = 2 × 5 and so on.
Q1: Share the patterns that you notice in the table.
Ans: We notice that each row/column is a multiple of its row/column number. Also its diagonal cells are all perfect squares.
Q2: Are the numbers in row 7 the same as the numbers in column 7? In general, are the numbers in a given row the same as the numbers in the corresponding column? Why does this happen?
Ans:
- Yes, row 7 = column 7 (7×1, 7×2, … = 1×7, 2×7, …).
- General: Row n = column n due to commutative property (a×b = b×a).
Q3: Is there a row where all answers (products) are even numbers? Which rows have this property
Ans: Rows 2, 4, 6, 8 (multiples of 2, 4, 6, 8 are even).
Q4: Is there a row having only odd numbers as products?
Ans: No; odd row (e.g., 7) has even products (e.g., 7×2 = 14).
Q5: Are there rows that have both even and odd numbers? What do you notice? Why is it so?
Ans: Yes, the rows of 1, 3, 5, 7, and 9 have both even and odd numbers. It is because when an odd number is multiplied with an even number, we get an even number, but when an odd number is multiplied with another odd number, we get an odd number.
Q6: Are there more even numbers in the chart or odd numbers? How do you know?
Ans: More even; even rows dominate, and odd rows have even products.
Q7: Colour the common multiples of the following numbers. Use different colours for each item.
(a) 2 and 3
Ans: LCM = 6; multiples: 6, 12, 18, …
(b) 4 and 8
Ans: LCM = 8; multiples: 8, 16, 24, …
(c) 7 and 9
Ans: LCM = 63; multiples: 63, 126, 189, …
Observation: Common multiples are less frequent for larger numbers.
Q8: Observe the pattern in the ones digits of the products in row 5? Observe the ones digit of the products in other rows also. What patterns do you notice?
Ans:
- Row 5: 5, 10, 15, …; ones: 5, 0, 5, 0, … (repeats).
- Row 8: 8, 6, 4, 2, 0, … (repeats every 5).
- Pattern: Ones digits cycle based on multiplier.
Q9: Here is row 8 of the chart: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80.
The ones digit of the products are: 8, 6, 4, 2, 0, 8, 6, 4, 2, 0.
Do you see a repeating pattern here?
Guess the ones digit of the following products. Verify your answer by multiplying. Write the digit in the space given.
(a) 11 × 8
(b) 12 × 8
(c) 13 × 8
Ans: Yes, the pattern of ones digits is 8, 6, 4, 2, 0 and is repeating.
Since 1 × 8 = 8,
2 × 8 = 16, 3 × 8 = 24. So, the ones digits of 11 × 8, 12 × 8, and 13 × 8 are 8, 6, and 4, respectively.
11 × 8 = 88 12 × 8 = 96 13 × 8 = 104
Q10: In row 8 of the chart, there is no number whose ones digit is 1. What other digits do not appear as the ones digit?
Ans: Row 8: 8, 6, 4, 2, 0. Missing: 1, 3, 5, 7, 9.
Q11: Is there a row in which all the digits from 0 to 9 appear as the ones digit? Which rows have this property?
Ans: Yes, rows 1, 3, 7, and 9 have this property.
Q12: It can be seen in row 8 that 0 appears as the ones digit two times.
____ × 8 gives 0 as the ones digit.
What numbers can go in the box? Give 5 examples of such numbers.
Ans: 5 × 8 = 40 or 10 × 8 = 80, gives 0 as the ones digit.
15 × 8 = 120, 20 × 8 = 160, 25 × 8 = 200, 30 × 8 = 240, 35 × 8 = 280.
Q13: Is there a row in which 0 appears as the ones digit only once? Which rows have this property?
Ans: Yes, the rows of 1, 3, 7, and 9 have this property.
Q14: What do you notice about the answers for Questions 11 and 13? Share in the grade.
Ans: Both have the same answers.
Page 137
Multiples of Tens

Q1: Let us count the number of wheels in tricycles.
(a) Number of wheels in 10 tricycles with 3 wheels in each is 10 × 3 wheels = ______ wheels.
Ans: Number of wheels in 10 tricycles with 3 wheels in each is 10 × 3 wheels = 30 wheels.
(b) Number of wheels in 10 more tricycles with 3 wheels in each is 10 × 3 wheels = _______ wheels.
Ans: Number of wheels in 10 more tricycles with 3 wheels in each is 10 × 3 = 30 wheels.
(c) Number of wheels in 20 tricycles with 3 wheels in each is 20 × 3 wheels = ______ + _____ = ______ wheels.
Ans: Number of wheels in 20 tricycles with 3 wheels in each is 20 × 3 wheels = 30 + 30 = 60 wheels.

Q2: Let us count the number of wheels in cars.
(a) Number of wheels in 10 cars with 4 wheels in each is 10 × 4 wheels = _______ wheels.
Ans: Number of wheels in 10 cars with 4 wheels in each is 10 × 4 wheels = 40 wheels.
(b) Number of wheels in 30 cars with 4 wheels in each is 30 × 4 wheels = _____ + _____ + _____ = _____ wheels.
Ans: Number of wheels in 30 cars with 4 wheels in each is 30 × 4 wheels = 40 + 40 + 40 = 120 wheels.
Q3: Solve the following in a similar way. Share how you found the answers.
(a) 10 × 6 = ________
Ans:
- Multiplication: 10 × 6 means 10 groups of 6.
- I know that 10 × 6 = 60 (using basic multiplication facts).
- Alternatively, think of it as adding 6 ten times: 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 = 60.
(b) 40 × 6 = ________
Ans:
- Break it down: 40 = 4 × 10, so 40 × 6 = (4 × 10) × 6.
- First, calculate 4 × 6 = 24.
- Then, multiply by 10: 24 × 10 = 240.
- Alternatively, use direct multiplication: 40 × 6 = 40 + 40 + 40 + 40 + 40 + 40 = 240.
(c) 10 × 8 = ________
Ans:
- Multiplication: 10 × 8 means 10 groups of 8.
- I know that 10 × 8 = 80 (using basic multiplication facts).
- Alternatively, add 8 ten times: 8 + 8 + 8 + 8 + 8 + 8 + 8 + 8 + 8 + 8 = 80.
(d) 60 × 8 = ________
Ans:
- Break it down: 60 = 6 × 10, so 60 × 8 = (6 × 10) × 8.
- First, calculate 6 × 8 = 48.
- Then, multiply by 10: 48 × 10 = 480.
- Alternatively, use direct multiplication: 60 × 8 = 60 + 60 + 60 + 60 + 60 + 60 + 60 + 60 = 480.
(e) 6 × 8 = ________
Ans:
- Multiplication: 6 × 8 means 6 groups of 8.
- I know that 6 × 8 = 48 (using basic multiplication facts, often memorized in Class 4).
- Alternatively, think of it as adding 8 six times: 8 + 8 + 8 + 8 + 8 + 8 = 48.
(f) 4 × 6 = ________
Ans:
- Multiplication: 4 × 6 means 4 groups of 6.
- I know that 4 × 6 = 24 (using basic multiplication facts).
- Alternatively, add 6 four times: 6 + 6 + 6 + 6 = 24.
(h) 40 × 8 = ________
Ans:
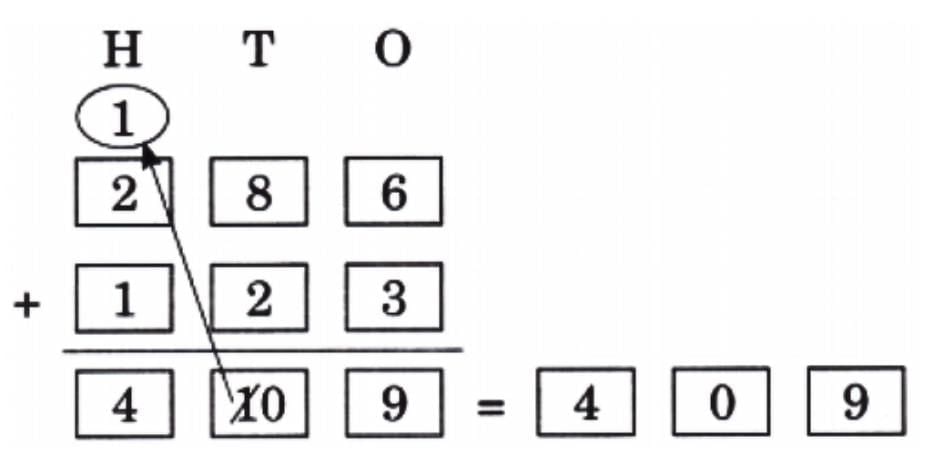
- Break it down: 40 = 4 × 10, so 40 × 8 = (4 × 10) × 8.
- First, calculate 4 × 8 = 32.
- Then, multiply by 10: 32 × 10 = 320.
- Alternatively, use direct multiplication: 40 × 8 = 40 + 40 + 40 + 40 + 40 + 40 + 40 + 40 = 320.
Q: What happens when the number of groups is a multiple of 10?
Ans: If a number of groups is a multiple of 10, then it always ends with 0 as ones digit.
Page 138
Multiplying Using 10s
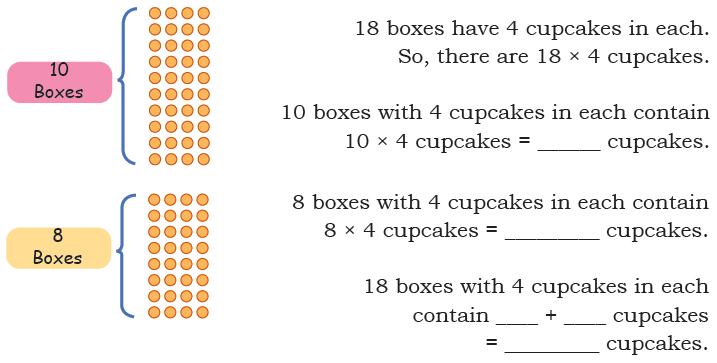
Q1: Radha is packing cupcakes in boxes of 4. She has packed 18 boxes. How many cupcakes are there in the packed boxes?
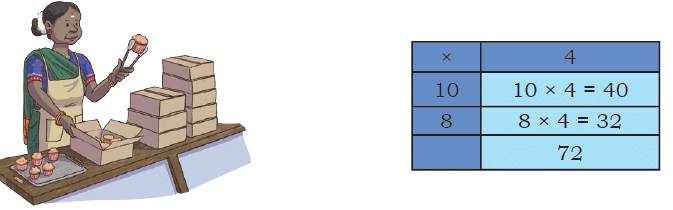
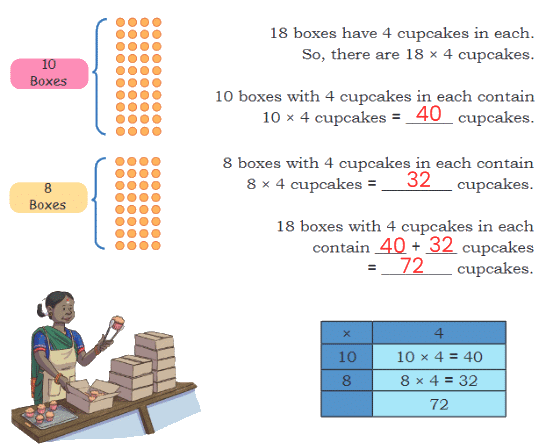
Ans:

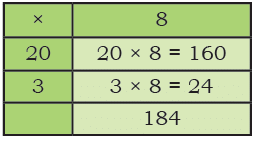
Q2: 8 bamboo rods are needed to make a bullock cart. How many bamboo rods are needed for 23 carts?
One cart needs 8 bamboo rods. 23 carts need 23 × 8 rods.
20 carts with 8 rods in each need 20 × 8 rods = ________ rods.
3 carts with 8 rods in each need 3 × 8 rods = _________ rods.
Ans: First, we calculate for 20 carts:
20 carts with 8 bamboo rods each = 20 × 8 = 160 rods.
Next, we calculate for 3 carts:
3 carts with 8 bamboo rods each = 3 × 8 = 24 rods.
Now, add the rods for all 23 carts:
160 + 24 = 184 rods.
So, 184 bamboo rods are needed for 23 carts.
Page 139
Let Us Solve
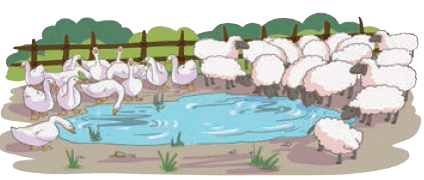
Q1: A flock of 25 geese and 12 sheep have gathered around a pond. Chippi the lizard sees many legs. How many legs does it see?
Ans: Each goose has 2 legs, and each sheep has 4 legs.
25 geese have, 25 × 2 legs = 50 legs
12 sheep have, 12 × 4 legs = 48 legs
Total legs seen by Chippi = 25 geese’s legs + 12 sheep’s legs = 50 legs + 48 legs = 98 legs.
Q2: In an auditorium, 8 children are sitting in each row. There are 15 such rows in the school auditorium. How many children are in the auditorium?
Ans: Children sitting in 1 row = 8
Children sitting in 15 rows = 15 × 8 = 120
So, 120 children are in the auditorium.
Q3: A book shop has kept 9 books in each pile. There are 14 such piles. How many books does the shop have?
Ans: 1 pile has 9 books.
14 piles have, 14 × 9 books = 126 books
So, the shop has a total of 126 books.

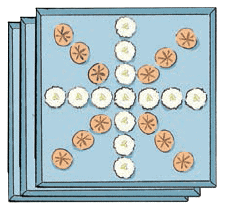
Q4: Surya is making a patch work with beads of two colours as shown in the picture. How many beads has he used? How many each of golden colour beads and white colour beads has he used in making this patch work?
Ans: Number of columns in the patch = 8
Number of beads in 1 column = 4 × 5 = 20
Total number of beads used by Surya = 20 × 8 = 160
Number of white beads in each consecutive 2 columns = 20,
so total number of white beads in the patch = 20 × 4 = 80
Also, Number of golden beads in each consecutive 2 columns = 20,
so total number of golden beads in the patch = 20 × 4 = 80.
Q5: For each of the following multiplication problems, make your own stories as above. Then find out the product.
a) 34 × 3 = 102
Story: There are 34 chairs, and each chair has 3 legs.
Answer: Total legs = 102
b) 75 × 5 = 375
Story: A classroom has 75 desks, and each desk has 5 books.
Answer: Total books = 375
c) 46 × 6 = 276
Story: A bus has 46 rows of seats, and each row has 6 seats.
Answer: Total seats = 276
d) 50 × 9 = 450
Story: A shopkeeper has 50 bags, and each bag contains 9 apples.
Answer: Total apples = 450
Page 140 & 141
Division
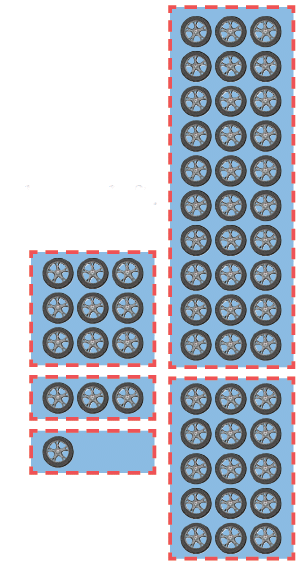
Q1: A factory has ordered 58 wheels for the small tempos that they make. Each tempo has 3 wheels. In how many tempos can they fix the wheels? Discuss your thinking in each step.
Number of tempos is 58 ÷ 3

30 wheels are needed for 10 tempos. _______wheels are left.
15 wheels are needed for _______ tempos. _______wheels are left.
9 wheels are needed for_______ tempos. _______ wheels are left.
_______ wheels are needed for_______ tempos. _______ wheels are left.
Can we make another tempo? How many total tempos can the factory make using the 58 wheels? ___
With 58 wheels, we can make 19 tempos. 1 wheel is left.
Ans: 58 ÷ 3 = 19 tempos, 1 wheel left.
Method:
- 10 tempos: 30 wheels, 58 − 30 = 28 left.
- 5 tempos: 15 wheels, 28 − 15 = 13 left.
- 3 tempos: 9 wheels, 13 − 9 = 4 left.
- 1 tempo: 3 wheels, 4 − 3 = 1 left.
- Total: 10 + 5 + 3 + 1 = 19 tempos.
- Ans: 19 tempos, 1 wheel left.
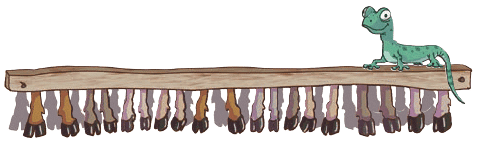
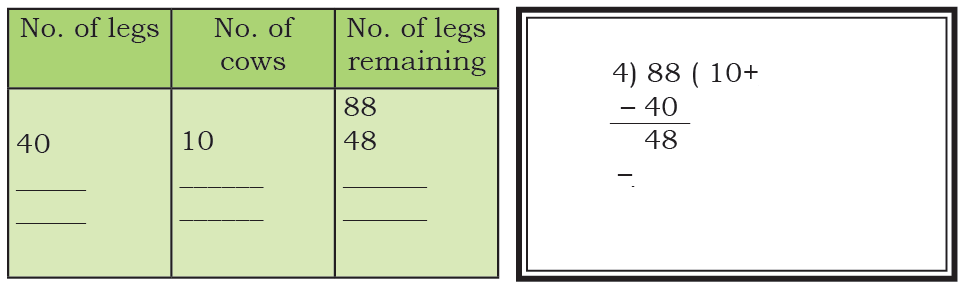

Q2: A dairy farm has many cows. Chippi the lizard is surprised to see 88 legs. How many cows are there in the farm? Write appropriate sentences as above to show your thinking.
Number of legs of a cow: ________
Number of cows is 88 ÷ ________
Show your work using the table below. Hint: Taking out groups of 10s is easy.
Total number of cows = ______
Ans: 88 ÷ 4 = 22 cows.
Method:
Total: 10 + 10 + 2 = 22 cows.
Ans: 22 cows.
Let Us Solve

Q1: In a big aquarium, Jolly fish sees 72 legs of octopuses. How many octopuses are there in the aquarium?
Ans: 72 ÷ 8 = 9 octopuses.
Method: 5 × 8 = 40, 4 × 8 = 32, 40 + 32 = 72, 5 + 4 = 9.
Ans: 9 octopuses.

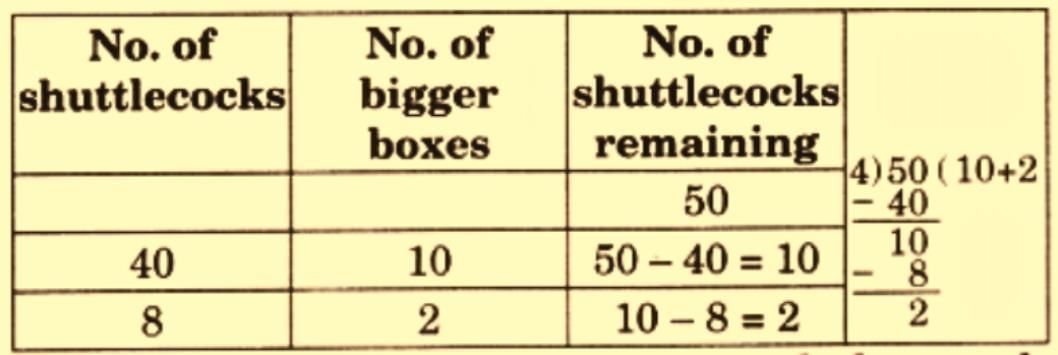
Q2: A sports store packs 4 shuttlecocks in a bigger box. They have 50 shuttlecocks. How many boxes will they need to pack all of them? Can they pack all the shuttlecocks in the boxes? How many are left?
Ans: 50 ÷ 4 = 12 boxes, 2 left.
Method: 10 × 4 = 40, 2 × 4 = 8, 40 + 8 = 48, 50 − 48 = 2.
Ans: 12 boxes, 2 shuttlecocks left.

Q3: Rakul Chachi uses a part of her farm to grow flowering plants for the upcoming festive season. She has planted 75 saplings of roses. Each row has 5 saplings. How many rows of saplings has she planted?
Ans: 75 ÷ 5 = 15 rows.
Method: 10 × 5 = 50, 5 × 5 = 25, 50 + 25 = 75, 10 + 5 = 15.
Ans: 15 rows.
Q4: Make stories for the following problems and solve them:
a) 70 ÷ 5
Story:
Riya has 70 candies. She wants to share them equally among 5 friends.
How many candies will each friend get?
Solution:
70 ÷ 5 = 14
Answer: Each friend will get 14 candies.
b) 84 ÷ 7
Story:A librarian has 84 books. She wants to place them equally on 7 shelves. How many books will go on each shelf?
Solution:
84 ÷ 7 = 12
Answer: Each shelf will have 12 books.
c) 69 ÷ 3
Story:
There are 69 eggs packed in trays. Each tray holds 3 eggs.
How many trays are needed?
Solution:
69 ÷ 3 = 23
Answer: She needs 23 trays.
d) 93 ÷ 6
Story:
A teacher has 93 chairs to arrange around 6 tables.
How many chairs will be around each table, and how many will be left?
Solution:
93 ÷ 6 = 15 remainder 3
Answer: Each table will get 15 chairs, and 3 chairs will be left.
Page 142

Multiples of 100
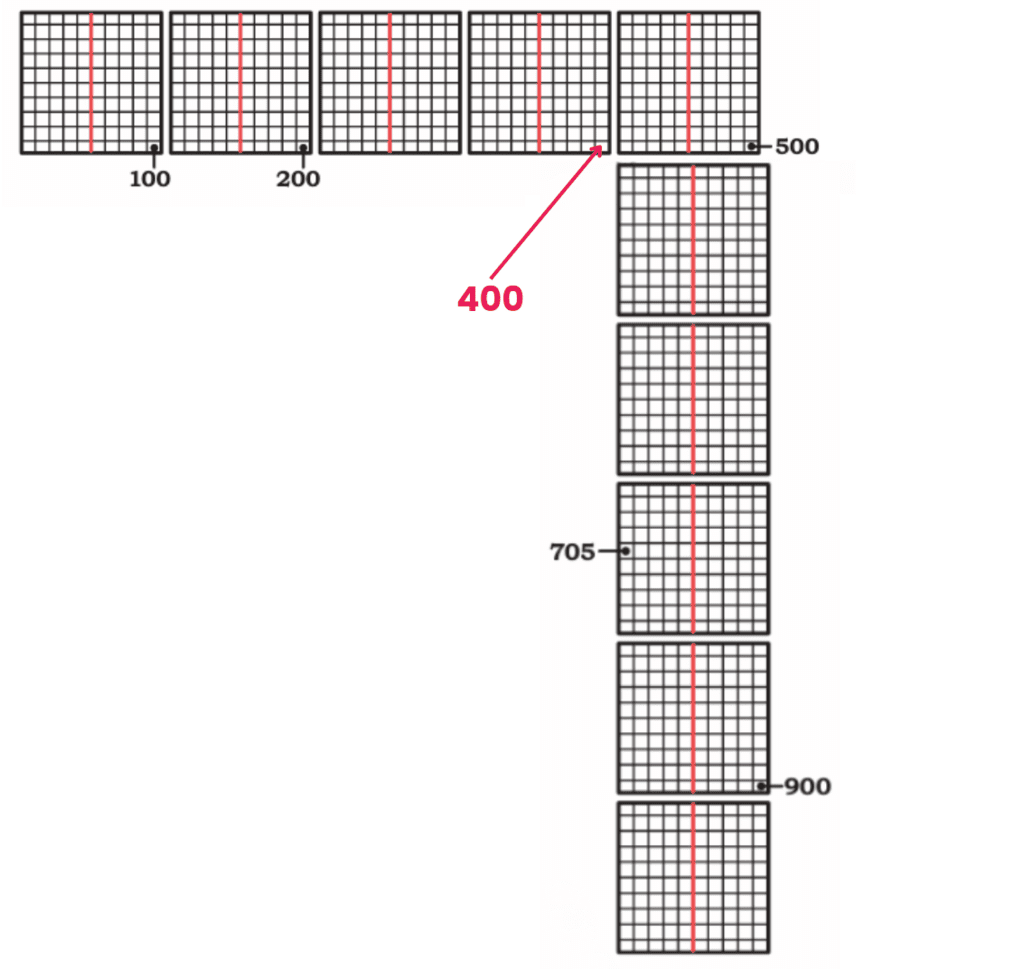
100 bikes with 2 people on each have 100 × 2 people = _____ people.
200 bikes with 2 people on each have ______people. How did you find it?
100 cars with 4 people in each have 100 × 4 people = _______ people.
500 cars with 4 people in each have ______people. How did you find it?
Ans: 100 bikes with 2 people on each have
= 100 × 2 people
= 200 people.
200 bikes with 2 people on each have
= 200 × 2 people
= 100 × 2 people + 100 × 2 people
= 200 people + 200 people
= 400 people.
100 cars with 4 people in each have
= 100 × 4 people
= 400 people.
500 cars with 4 people in each have
= 500 × 4 people
= (100 × 4 + 100 × 4 + 100 × 4 + 100 × 4 + 100 × 4)
= (400 + 400 + 400 + 400 + 400) people
= 2000 people.
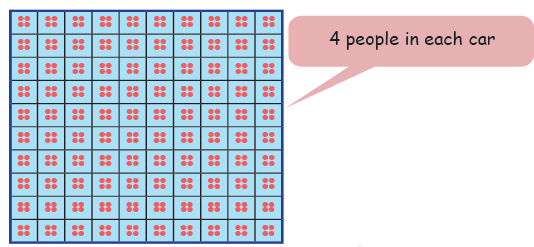
How did you find it?
500 × 4 = _____
100 × 4 = _____
5 × 4 = _____
50 × 4 = _____
Ans:
We multiplied the number of bikes by the number of people on each bike.
500 × 4 = 2000
5 × 4 = 20
100 × 4 = 400
50 × 4 = 200
What do you notice about multiplying by multiples of 100s?
- Ignore the zeros, multiply the other numbers, then add two zeros at the end.
Examples:
- 6 × 100 = 600 (6 × 1 = 6, add two zeros)
- 4 × 300 = 1200 (4 × 3 = 12, add two zeros)
Rule:
Multiply the main numbers, then add 00.
Page 143
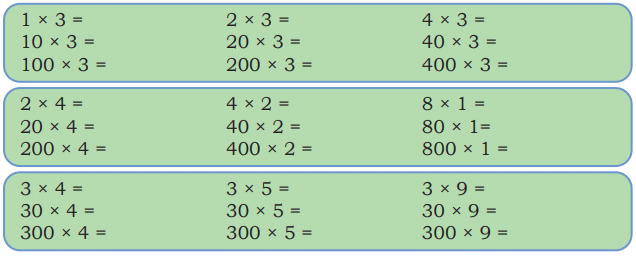
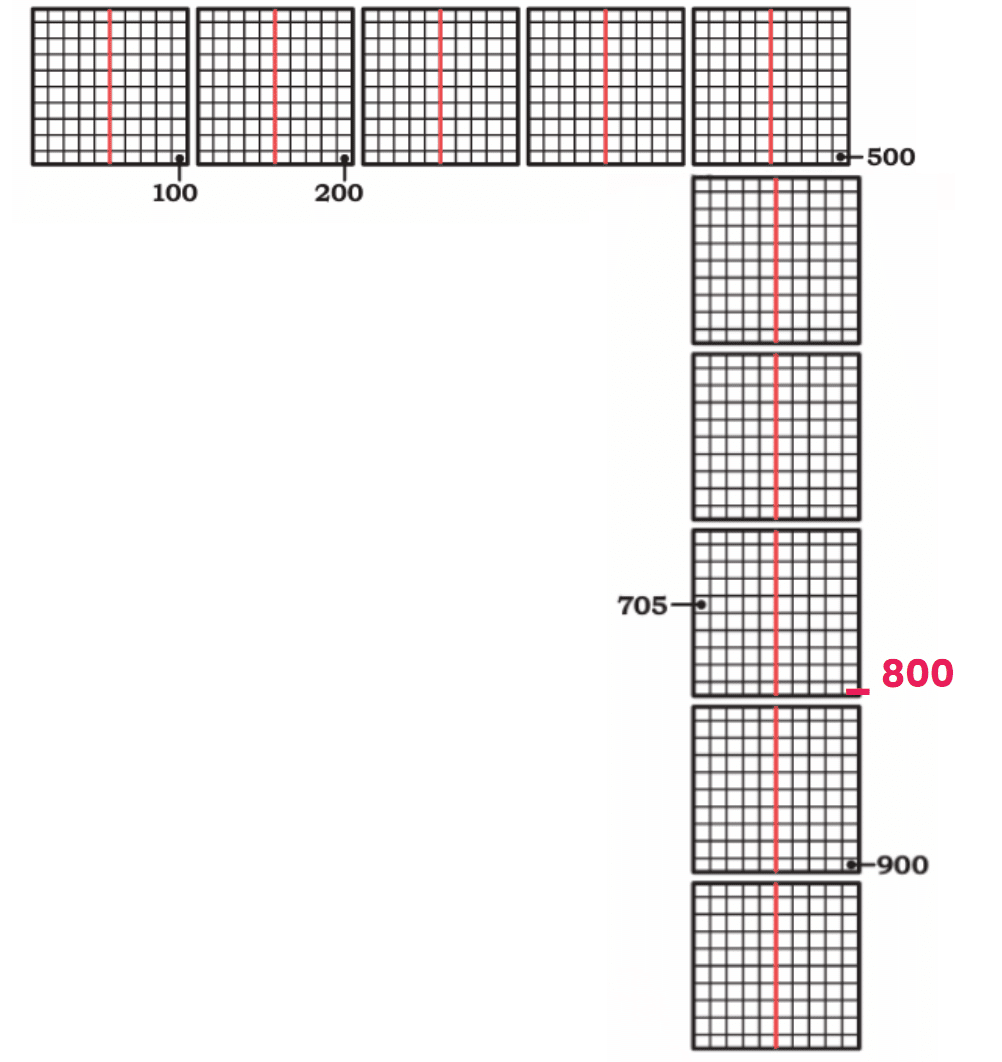
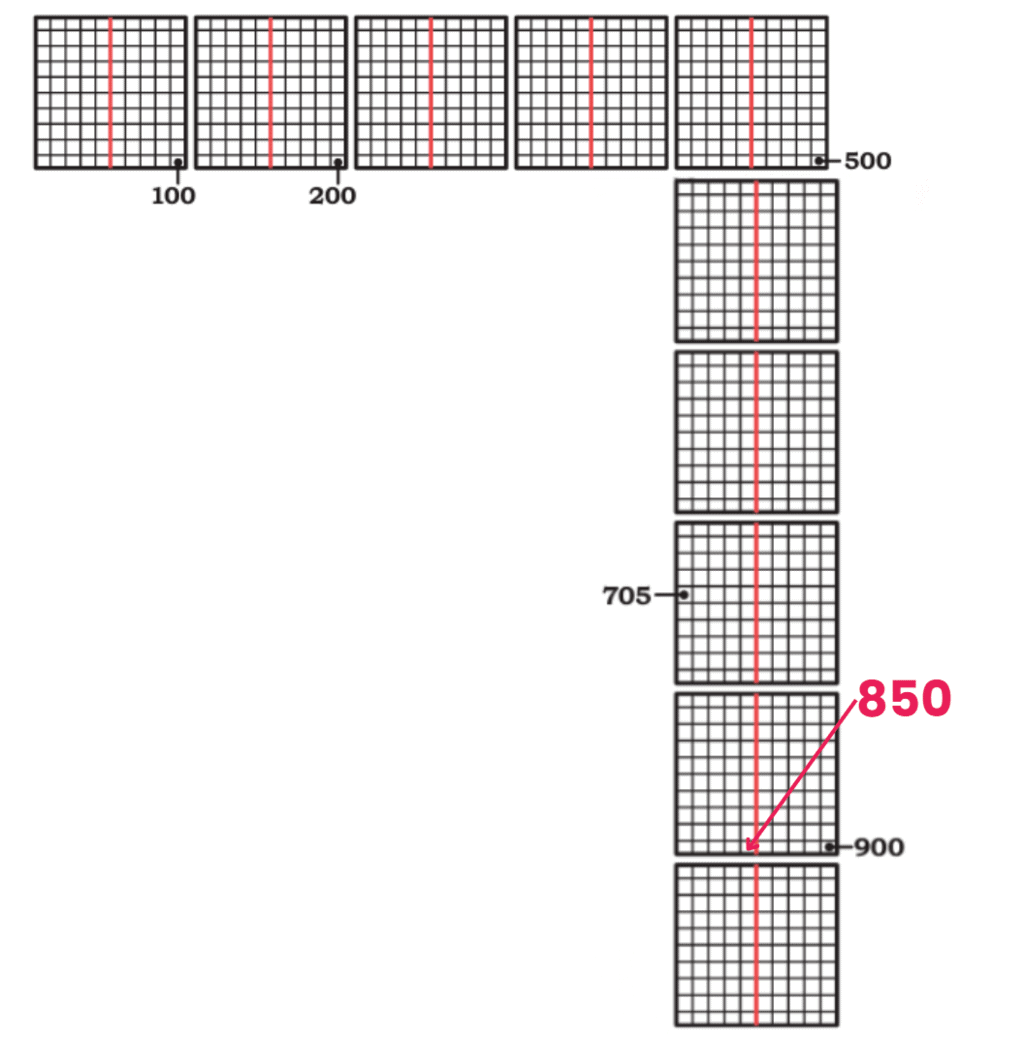
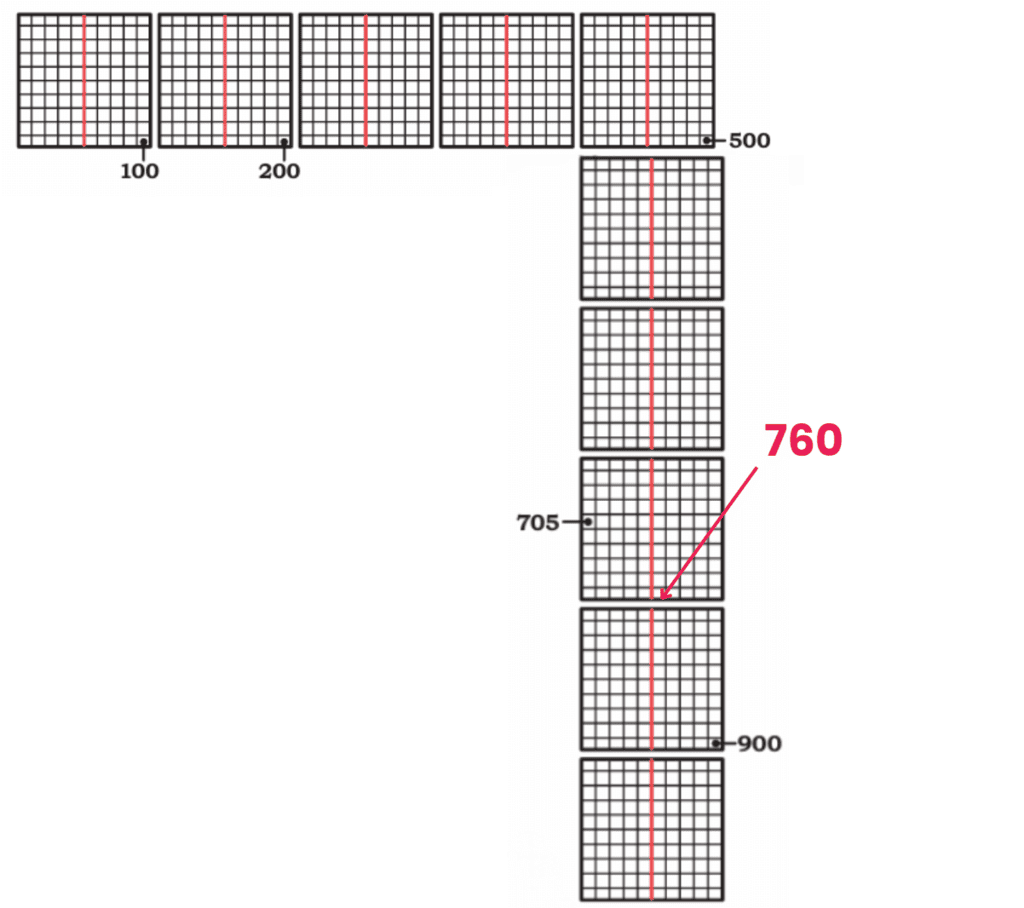
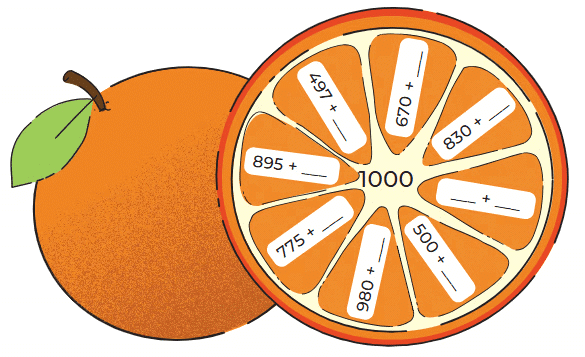
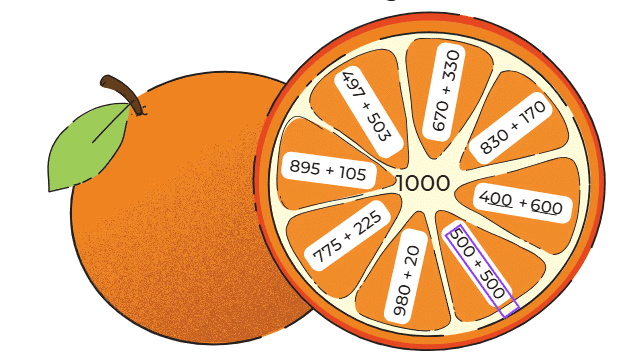
Q: Observe the pattern and complete the answers.

Ans:
Page 143
More Multiplication

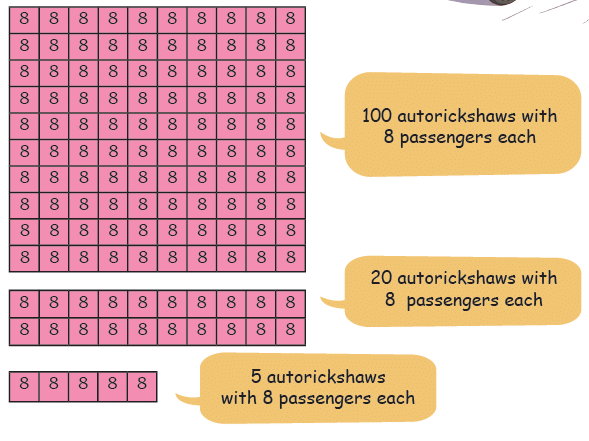
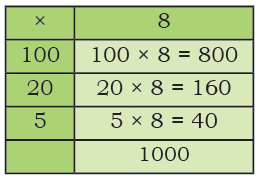
Q1: Big electric autorickshaws run in small towns of India and can carry 8 passengers. How many people can travel in 125 such autos in a single round?
The total number of passengers 125 × 8.
100 autorickshaws with 8 passengers in each have 100 × 8 passengers = ______ passengers.
20 autorickshaws with 8 passengers in each have 20 × 8 passengers = _______ passengers.
5 autorickshaws with 8 passengers in each have 5 × 8 passengers = __________ passengers.
125 autorickshaws with 8 passengers in each have ____ + ____ + ______= _________ passengers.
Ans: The total passengers are 125 100 autorickshaws with 8 passengers in each have
= 100 × 8 passengers
= 800 passengers
20 autorickshaws with 8 passengers in each have = 20 × 8 passengers = 160 passengers
5 autorickshaws with 8 passengers in each have = 5 × 8 passengers = 40 passengers
125 autorickshaws with 8 passengers in each have = 800 + 160 + 40 = 1000 passengers

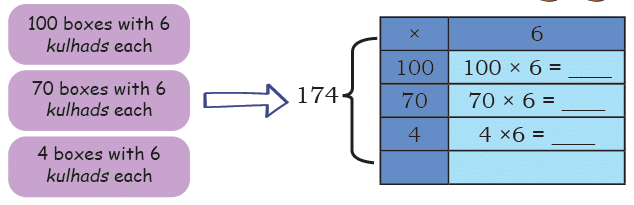
Q2: Kahlu and Rabia are potters and make earthen pots (kulhad) for trains.
They pack 6 kulhads in a box and have packed 174 boxes for delivery. How many kulhads have they made?
The total number of kulhads is ________.
Ans: The total number of kulhads is 174 × 6 = 600 + 420 + 24 = 1044
Page 144 & 145
Let Us Solve

Q1: BP Girl’s school has decided to give all its students two pencils on the first day of school. It has 465 students. How many pencils does the school need to buy?
Ans: Number of pencils given to each student = 2
Total number of students = 465
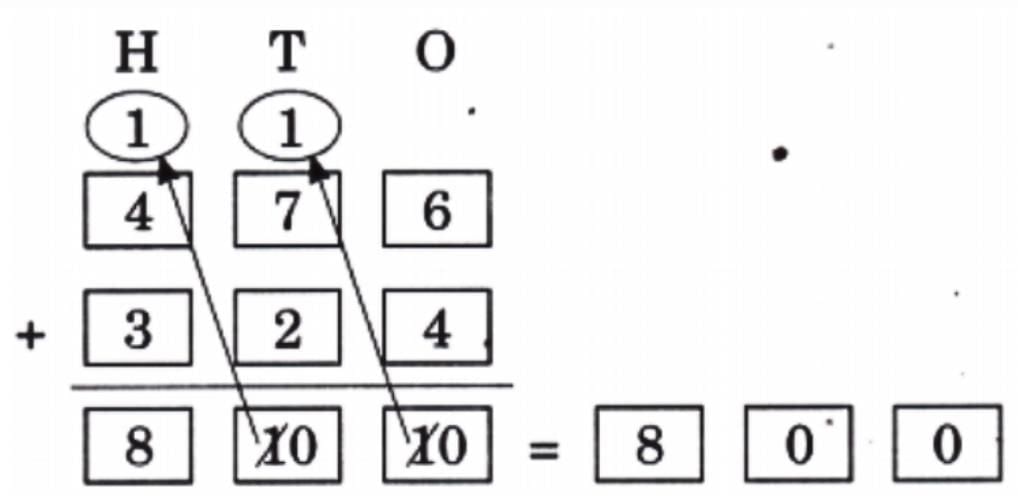
Total pencils school need to buy = 465 × 2 = 800 + 120 + 10 = 930
Q2: 234 children of a school have decided to organise a school mela. Each child contributes ₹5 for the organisation of the mela. How much money do they collect?
Ans: Money contributed by each child = ₹ 5
Total children in school mela = 234
Money collected for school mela = 234 × ₹ 5

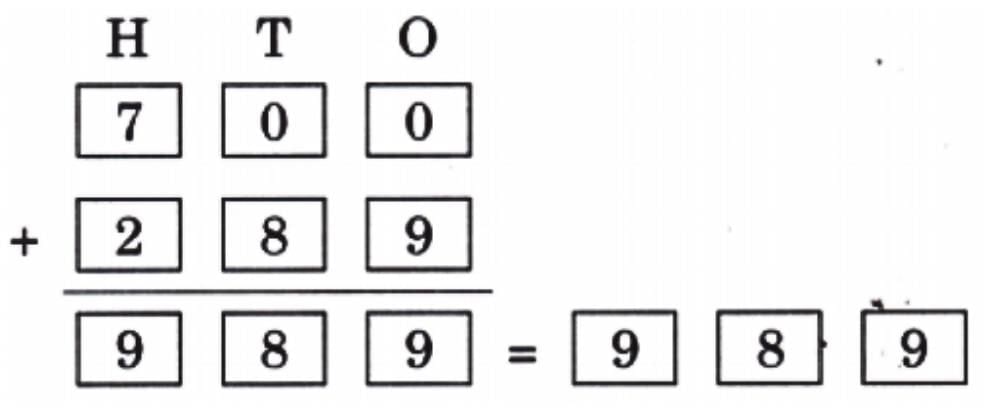
The total money collected from 234 children, with each contributing ₹ 5 = ₹ 1000 + ₹ 150 + ₹ 20 = ₹ 1170
Q3: Make stories for the following problems and solve them.
a) 439 × 4
Story:
A school has 439 students in each house. There are 4 houses in the school.
How many students are there in total?
Solution:
439 × 4 = 1,756
Answer: There are 1,756 students in total.
b) 514 × 8
Story:
A library has 514 books on each shelf. There are 8 shelves.
How many books are there in all?
Solution:
514 × 8 = 4,112
Answer: The library has 4,112 books.
c) 356 × 5
Story:
A factory packs 356 toys in each box. There are 5 boxes.
How many toys are packed?
Solution:
356 × 5 = 1,780
Answer: There are 1,780 toys packed.
d) 623 × 7
Story:
There are 623 apples in each basket. A farmer has 7 baskets.
How many apples does the farmer have?
Solution:
623 × 7 = 4,361
Answer: The farmer has 4,361 apples.
Page 146
Patterns in Division

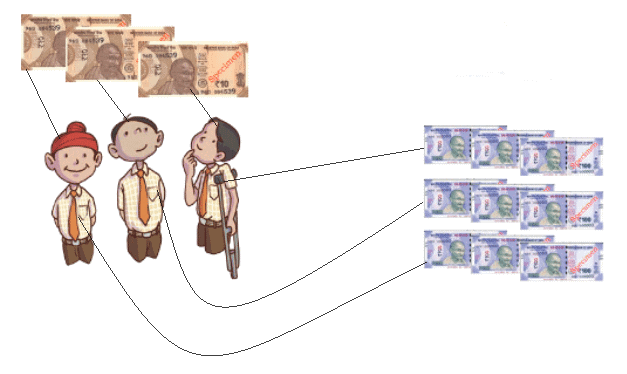
How much money will each get? Draw arrows linking the money and the children to answer the questions.
Ans:
1. ₹ 30 shared equally among 3 children ______________
We divide ₹30 by 3:
- ₹30 ÷ 3 = ₹10
Each child will get ₹10
2. ₹ 900 shared equally among 3 children ______________
We divide ₹900 by 3:
- ₹900 ÷ 3 = ₹300
Each child will get ₹300
Ans:
Q1: A load carrying truck has 6 tyres. Chippi the lizard sees 60 tyres. How many trucks are there?
Ans: We know 1 truck has 6 tyres.
If there are 60 tyres, we divide:
60 ÷ 6 = 10 trucks
(Each truck has 6 tyres. So 10 trucks × 6 tyres = 60 tyres)
Q2: Chippi sees 80 wheels in a car parking space. How many cars are standing in the parking space?
Ans: We know 1 car has 4 wheels.
If there are 80 wheels, we divide:
80 ÷ 4 = 20 cars
(Each car has 4 wheels. 20 × 4 = 80 wheels)
Q3: Chippi sees 600 legs of ants walking towards the anthill. How many ants are there?
Ans: We know 1 ant has 6 legs.
If there are 600 legs, we divide:
600 ÷ 6 = 100 ants
(Each ant has 6 legs. 100 × 6 = 600 legs)
Q4: A fancy shop has packed 800 rubber bands in several packets. Each packet has 4 rubber bands. How many packets of rubber bands does the shop have?
Ans: We know 1 packet = 4 rubber bands
If there are 800 rubber bands, we divide:
800 ÷ 4 = 200 packets
(Each packet holds 4 rubber bands. 200 × 4 = 800)
Page 147
Let Us Solve
Q1: A school bus hires 7 buses to take 245 children to the transport museum. Each bus carry the same number of children. How many children are traveling in each bus?
Ans: 245 ÷ 7 = 35 children/bus.
Method: 30 × 7 = 210, 5 × 7 = 35, 210 + 35 = 245, 30 + 5 = 35.
35 children/bus.

Q2: The Darjeeling Himalayan Railway is fondly called the “Toy Train”. This toy train ride is also a UNESCO World Heritage Site. This amazing train runs between New Jalpaiguri and Darjeeling and it also passes through one of the highest stations in the world, namely, Ghum. It runs 88 km daily. How much distance does it travel in a week?
Ans: 88 × 7 = 616 km.
Method: 80 × 7 = 560, 8 × 7 = 56, 560 + 56 = 616.
Q3: The 16 Km river rafting from Shivpuri to Rishikesh in the Ganga provides the most interesting rafting opportunity. In the summer months, Venture Out company took 259 people for rafting. Each raft can take 7 people. How many rafts did it take?
Ans: 259 ÷ 7 = 37 rafts.
Method: 30 × 7 = 210, 7 × 7 = 49, 210 + 49 = 259, 30 + 7 = 37.
Ans: 37 rafts.
Q4: Anu saves ₹45 every month by putting it in her piggy bank.
(a) How much money will Anu save in 6 months?
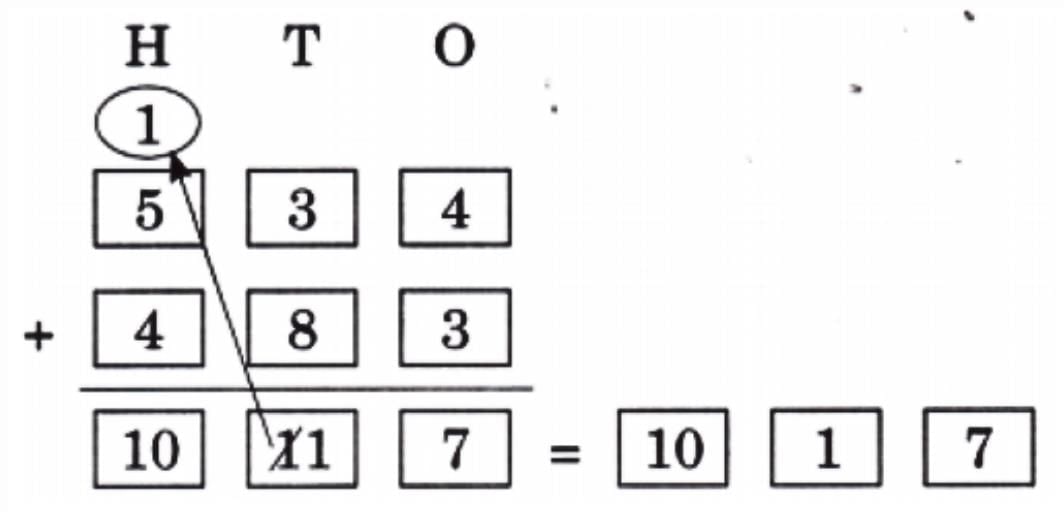
Ans: Money saved by Anu in 6 months = ₹ 45 × 6 = ₹ 40 × 6 + ₹ 5 × 6 = ₹ 240 + ₹ 30 = ₹ 270
(b) She distributes the total money saved after 6 months among 6 of her friends. How much does each friend get?
Ans: Total money distributed equally 210 among 6 friends.
So, money got by each 90- friend = ₹ 270 ÷ 3
= ₹(10 + 10 + 10 + 10 + 5)
= ₹ 45
(c) If she decides to distribute the saved money among 3 friends after 6 months, how much money will each get?
Ans: Money saved by Anu in 6 months = ₹ 270
Money got by each of 3 friends = ₹ 270 – 3
= ₹ (10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10) = ₹ 90
Q5: Raju drives an auto in his village and takes people to the bus stand. He makes 8 trips in a day. Which of the following questions can be exactly calculated with the above statement?
(a) How much money does he make in a day?
Ans: We cannot say how much money he makes in a day as the price of each trip is not given.
(b) How many trips does he make in 7 days?
Ans: Number of trips made in 7 days = 8 trips × 7 = 56 trips.
(c) How much time does one trip take?
Ans: We cannot say how much time he takes for a trip, as time is not mentioned.
(d) How many trips does he make in 4 weeks?
Ans: Number of trips in a week (7 days) = 8 × 7 = 56
Number of trips in 4 weeks = 56 × 4 = 50 × 4 + 6 × 4 = 200 + 24 = 224.
Page 148
Let Us Solve
Q6: Solve:
(a) 45 × 9
Ans: 405 (40 × 9 = 360, 5 × 9 = 45, 360 + 45 = 405)
(b) 507 × 7
Ans: 3549 (500 × 7 = 3500, 7 × 7 = 49, 3500 + 49 = 3549)
(c) 94 ÷ 4
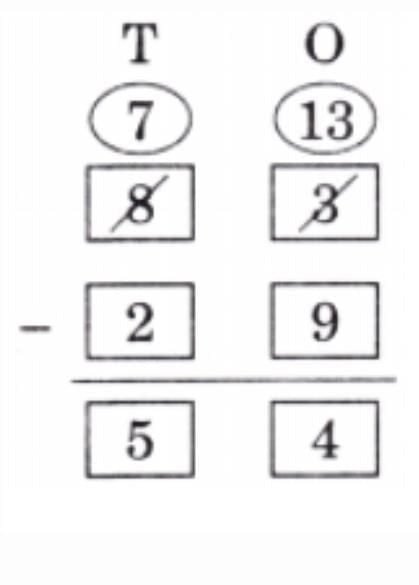
Ans: 23, remainder 2 (20 × 4 = 80, 3 × 4 = 12, 80 + 12 = 92, 94 − 92 = 2)
(d) 778 ÷ 6
Ans: 129, remainder 4 (100 × 6 = 600, 20 × 6 = 120, 9 × 6 = 54, 600 + 120 + 54 = 774, 778 − 774 = 4)
(e) 94 × 5
Ans: 470 (90 × 5 = 450, 4 × 5 = 20, 450 + 20 = 470)
(f) 396 × 4
Ans: 1584 (300 × 4 = 1200, 90 × 4 = 360, 6 × 4 = 24, 1200 + 360 + 24 = 1584)
(g) 83 ÷ 3
Ans: 27, remainder 2 (20 × 3 = 60, 7 × 3 = 21, 60 + 21 = 81, 83 − 81 = 2)
(h) 635 ÷ 5
Ans: 127 (100 × 5 = 500, 20 × 5 = 100, 7 × 5 = 35, 500 + 100 + 35 = 635, 100 + 20 + 7 = 127)
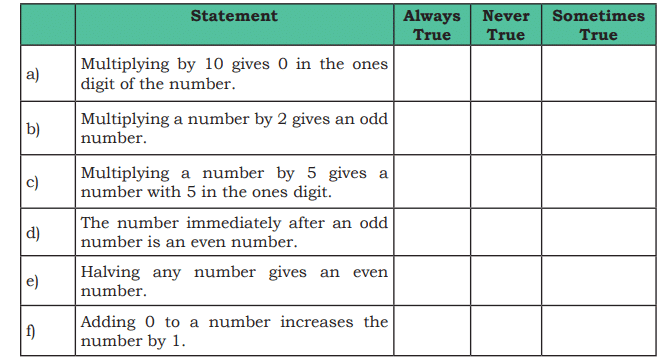
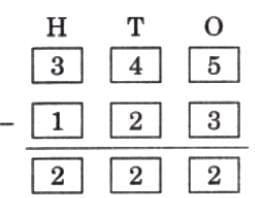
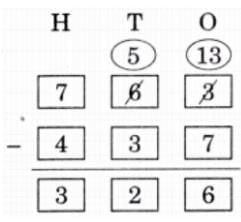
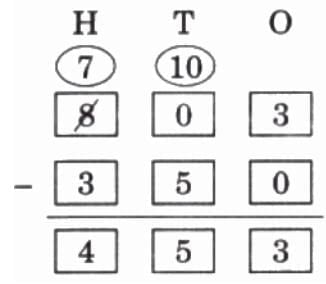
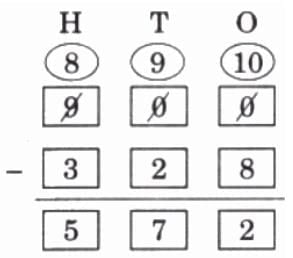
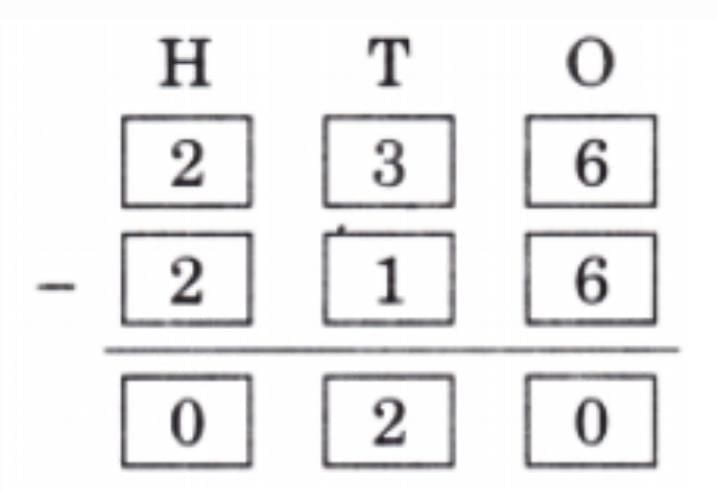
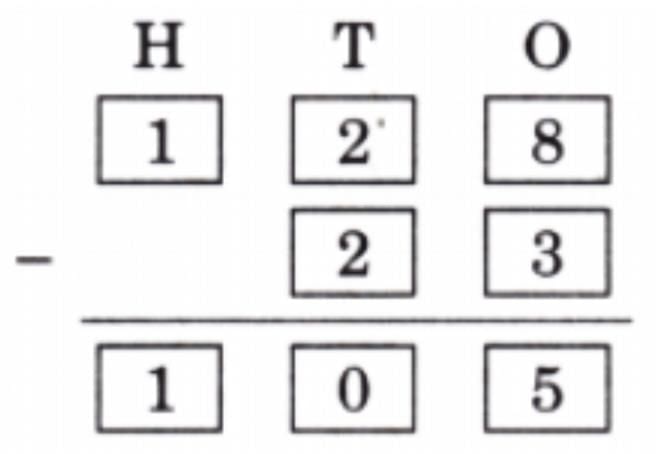
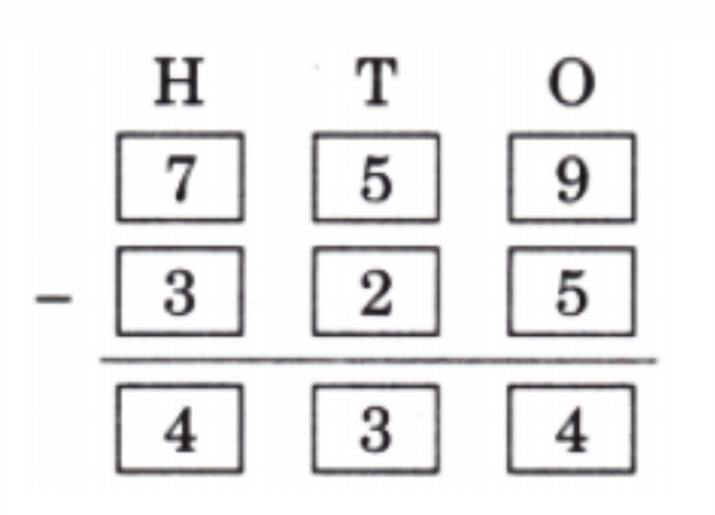
Q7: In mathematics, some statements are always true, some are sometimes true, and some are never true.
Tick (√) in the appropriate column.
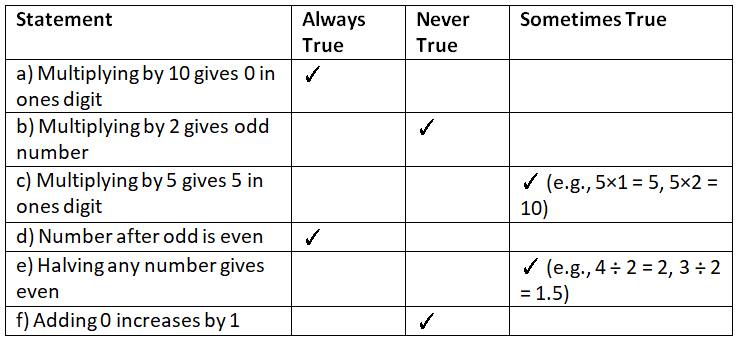
Ans:
















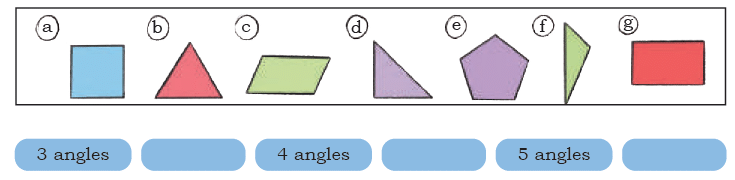
 Vertices: 1, 2, 3; Sides: 4, 5, 6
Vertices: 1, 2, 3; Sides: 4, 5, 6

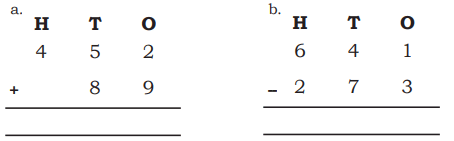
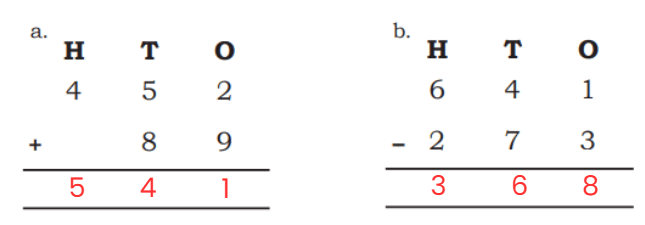

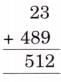
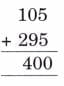
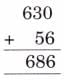
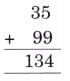
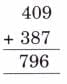
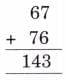
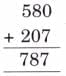

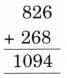
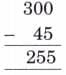

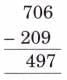
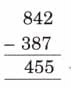
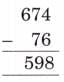

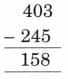
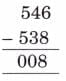
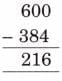






















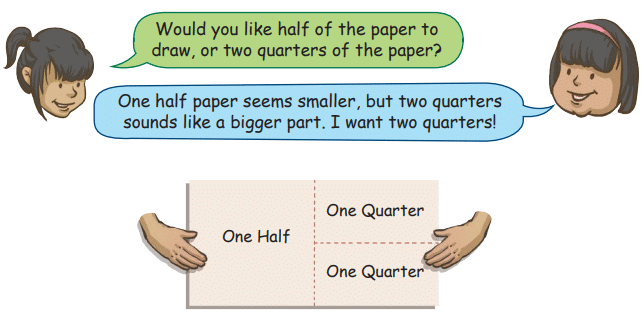
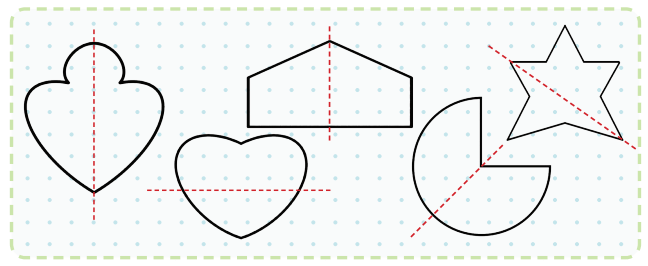
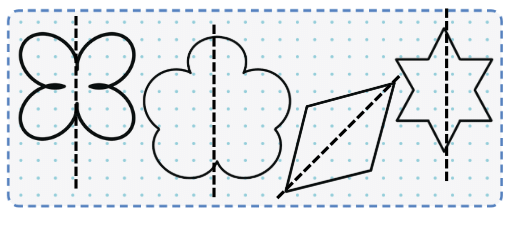
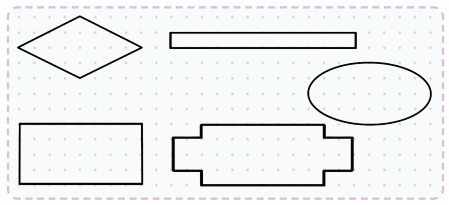
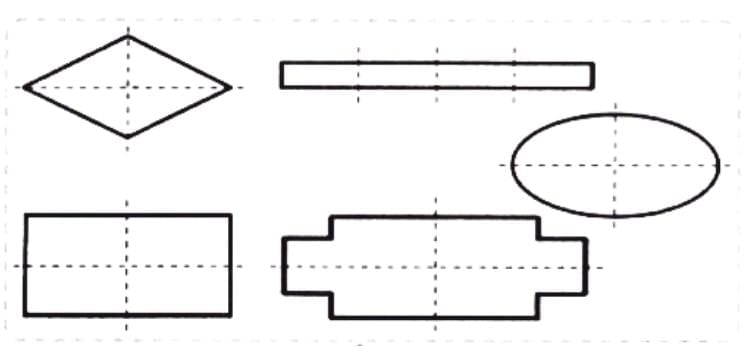
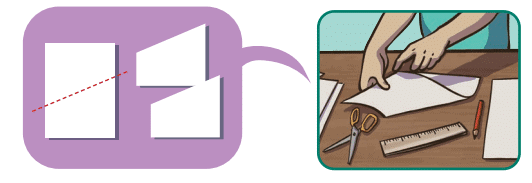
 Fold vertically to make two equal rectangles.
Fold vertically to make two equal rectangles. Fold horizontally to make two equal rectangles.
Fold horizontally to make two equal rectangles. Fold diagonally from one corner to the opposite corner to make two equal triangles.
Fold diagonally from one corner to the opposite corner to make two equal triangles.
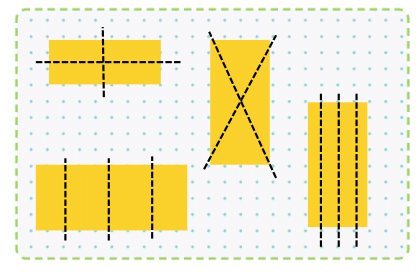 Draw two diagonal lines from opposite corners to make four equal triangles.
Draw two diagonal lines from opposite corners to make four equal triangles.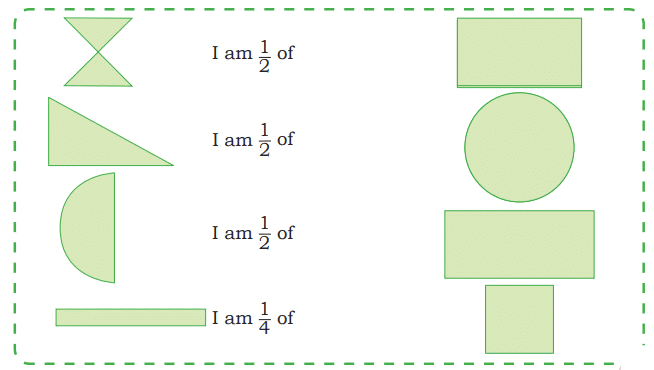
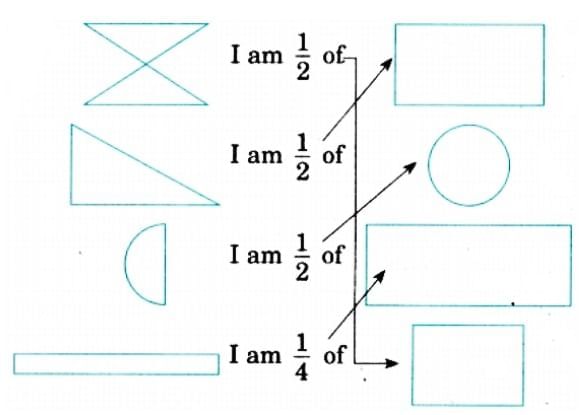

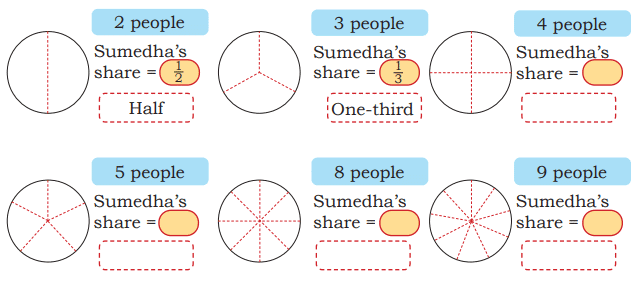
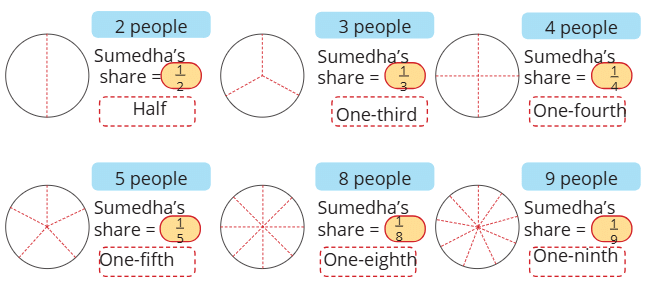
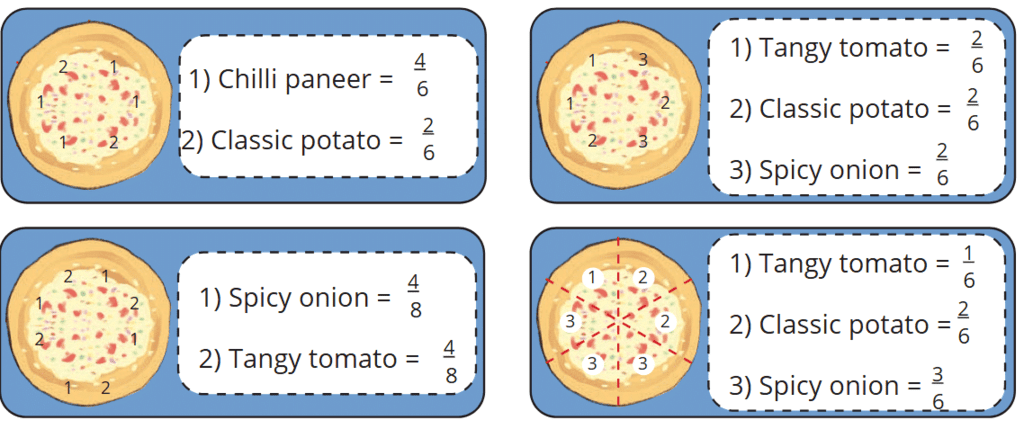
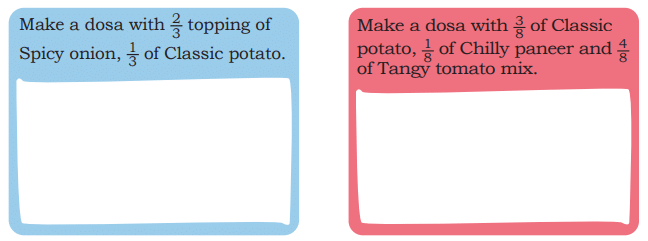
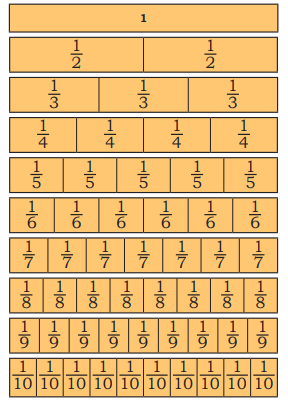
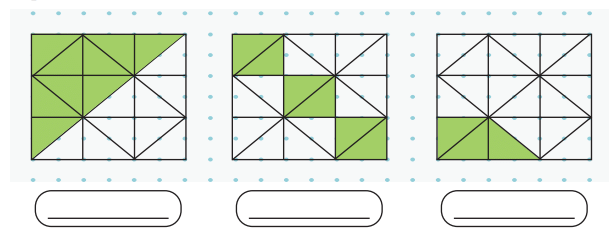
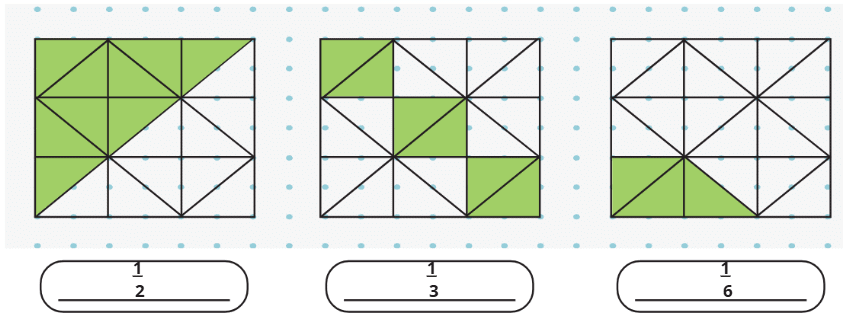
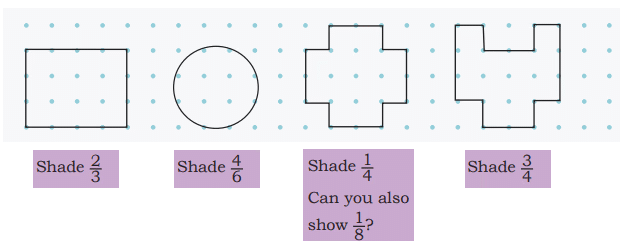
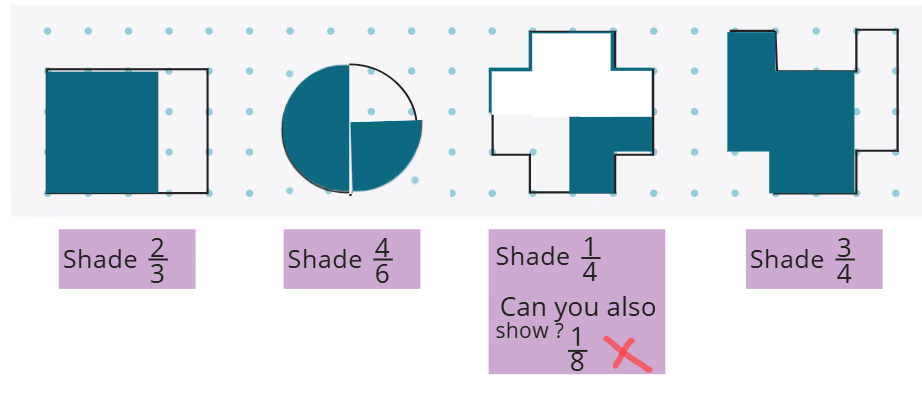
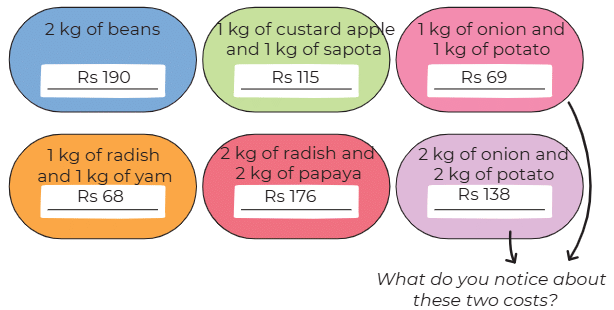
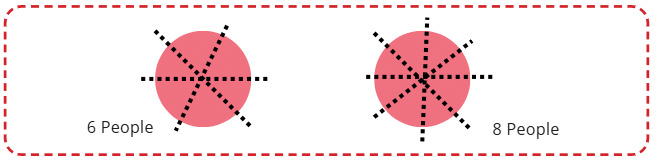 Explanation: The pieces are bigger when shared among 6 people because 1/6 is larger than 1/8. Draw a circle for the dhokla, divide it into 6 parts, and then into 8 parts to see that 1/6 is bigger.
Explanation: The pieces are bigger when shared among 6 people because 1/6 is larger than 1/8. Draw a circle for the dhokla, divide it into 6 parts, and then into 8 parts to see that 1/6 is bigger.