Text Book Solutions All Class

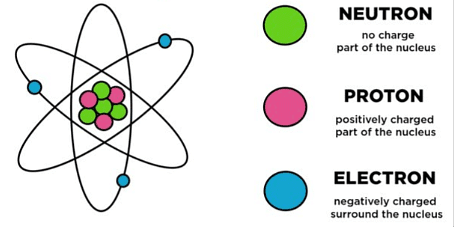
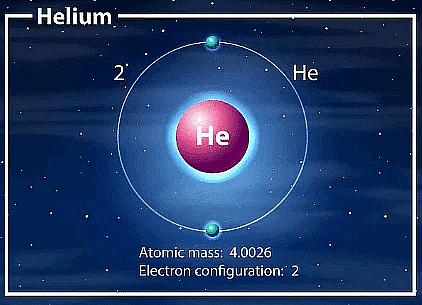
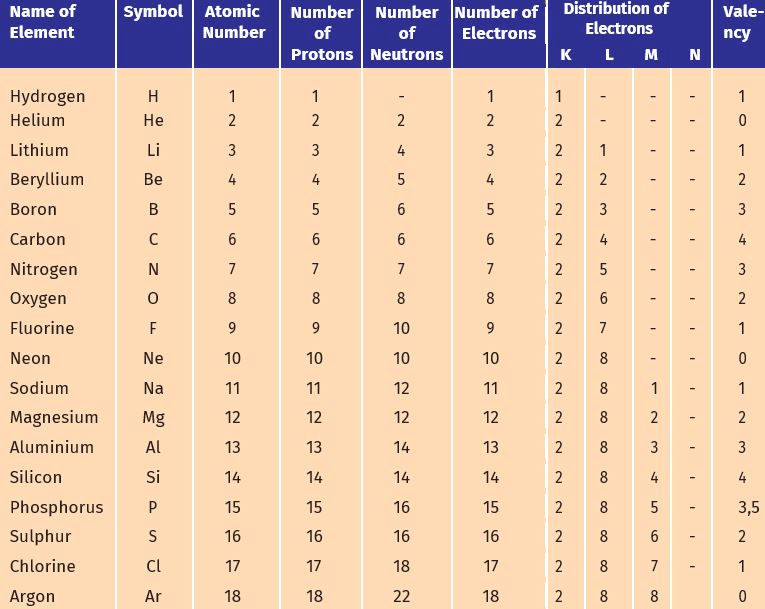
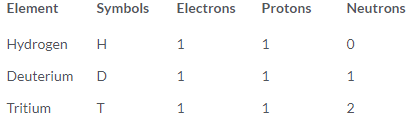
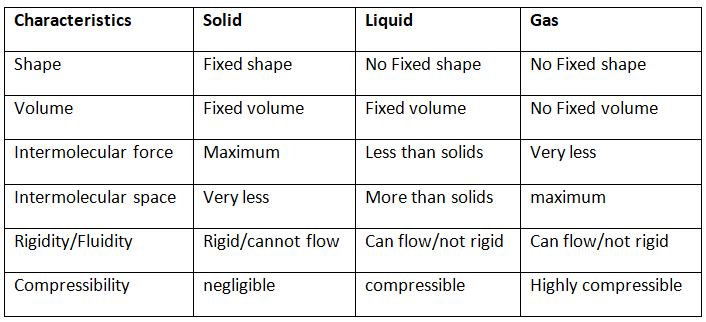
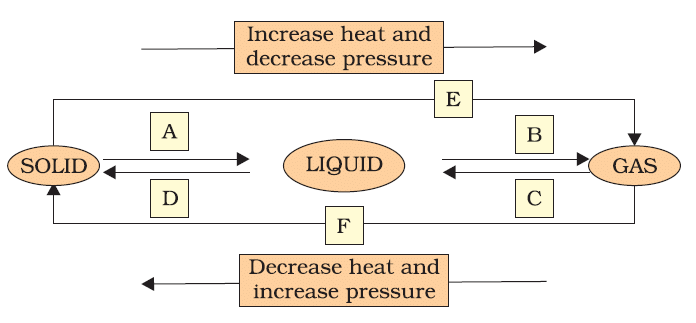
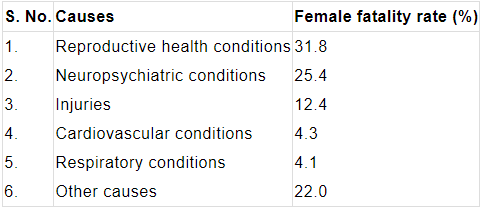
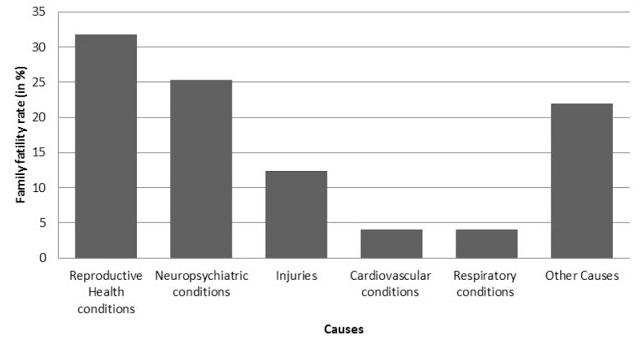
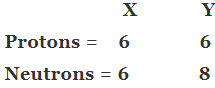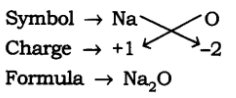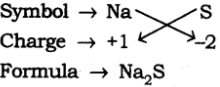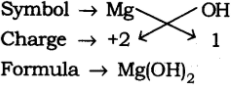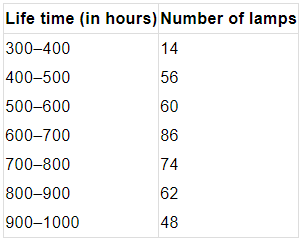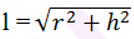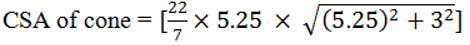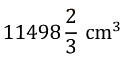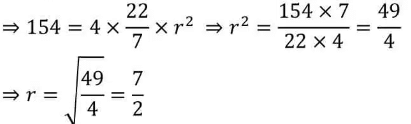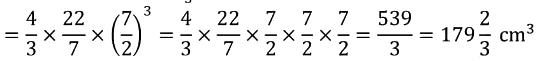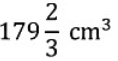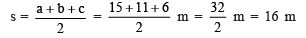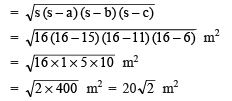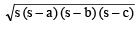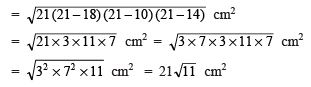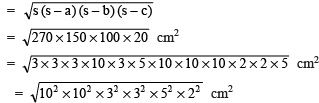Page No. 51

Q1. Who discovered cells and how?
Ans:

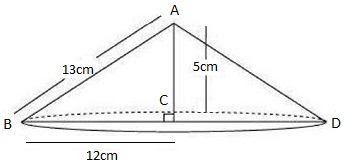
• The cell was first discovered by Robert Hooke in 1665. He examined thin slices of cork under a self-made microscope and saw a multitude of tiny hollow spaces that he remarked looked like the walled compartments of a honeycomb. 
• He termed these spaces as ‘cell’ meaning ‘small room’ in Latin.
  Microscope and Cork cells

Q2. Why is the cell called the structural and functional unit of life?
Ans:

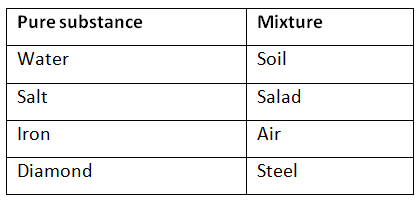
• All living organisms are made up of cells. This shows that the cell is the structural unit of life. 
• Each living cell can perform certain basic functions that are characteristic of all living forms. 
  Example: 
  (i) Phagocytic cells eat or kill unwanted or foreign particles inside the body (e.g., WBCs). 
  (ii) Some cells secrete enzymes and hormones, e.g., pancreatic cells, small intestinal cells, and liver cells.

Page No. 53

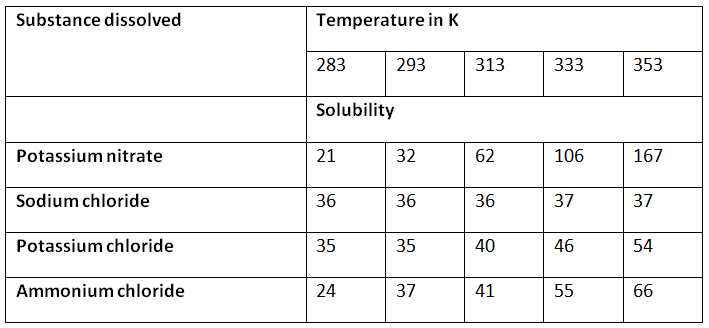
Q1. How do substances like CO₂ and water move in and out of the cell? Discuss.
Ans: CO₂ moves by diffusion – This cellular waste accumulates in high concentrations in the cell, whereas the concentration of CO₂ in the external surroundings is comparatively lower. This difference in the concentration level inside and outside of the cell causes the CO₂ to diffuse from a higher (within the cell) region to a lower concentration.
H₂O diffuses by osmosis through the cell membrane. It moves from a region of higher concentration to a lower concentrated region through a selectively permeable membrane until equilibrium is reached.

Q2. Why is the plasma membrane called a selectively permeable membrane?
Ans: The plasma membrane allows or permits the entry and exit of some materials in and out of the cell and prevents the movement of some other materials through it. Hence, it is called a selectively permeable membrane.Page No. 55

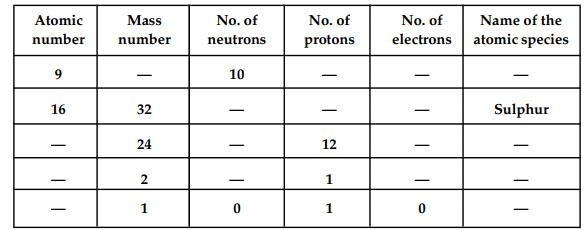
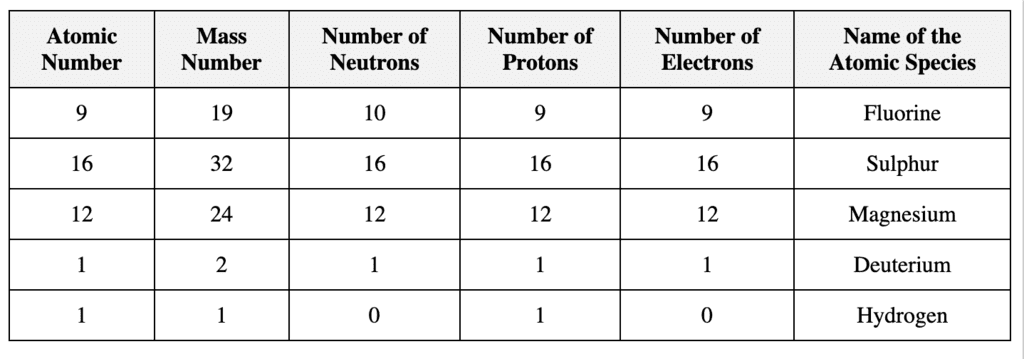
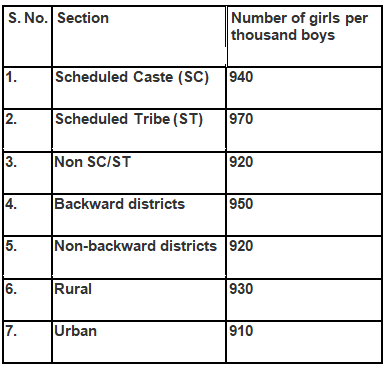
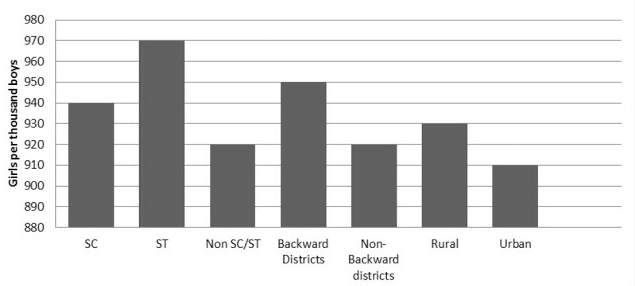
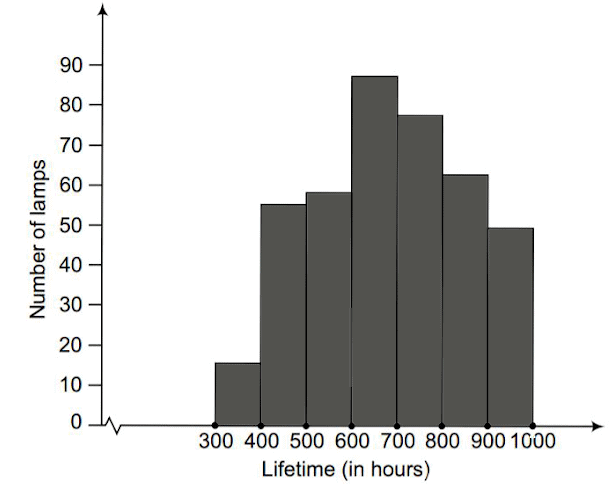
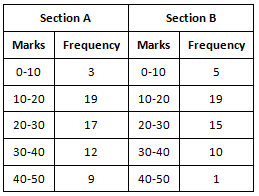
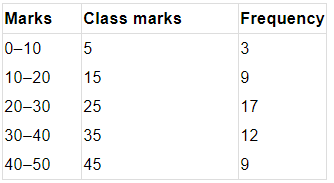
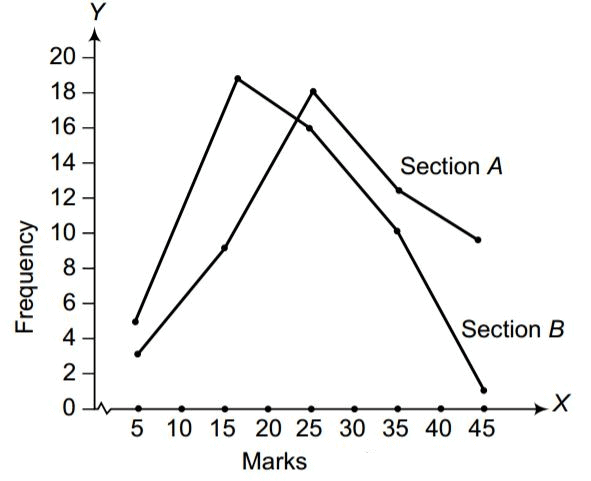
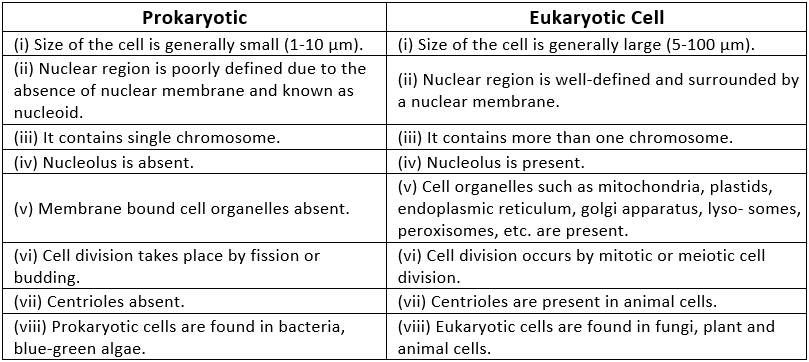
Q1. Fill in the gaps in the following table illustrating the differences between prokaryotic and eukaryotic cells.

Ans:Page No. 57

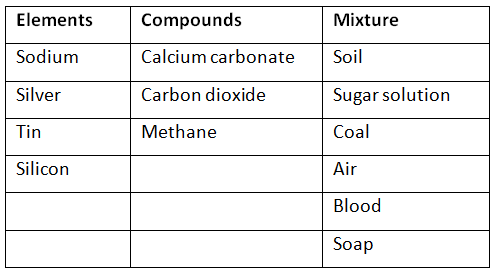
Q1. Can you name the two organelles we have studied that contain their genetic material?
Ans: Two organelles that contain their genetic material are Mitochondria and Plastids. Mitochondria help in respiration in the cell, while plastids are responsible for the process of photosynthesis in leaves. 

Q2. If the organization of a cell is destroyed due to some physical or chemical influence, what will happen?
Ans:

• Cell organelles are responsible for the organization and proper functioning of a cell, as each of them performs some specific functions. 
• Naturally, if any of these organelles are destroyed, the cell will not be able to perform many basic functions like photosynthesis, respiration, nutrition, etc., and may also result in the stopping of all life activities in the cell. Due to the cell damage, the lysosome bursts, and their enzymes digest such cells.

Q3. Why are lysosomes known as suicide bags?
Ans:

• Lysosomes are the cell organelles involved in the digestion of any foreign material that enters the cell, as they contain digestive enzymes. 
• In case any cell is dead or damaged, the lysosome bursts to release the digestive enzymes to digest its cell. 
• Thus, these are known as ‘suicide bags’.

Q4. Where are proteins synthesized inside the cell?
Ans:

• Proteins are the building blocks of the body that are made up of various amino acids. They are synthesized inside the ribosomes, are the small structures present in the cytoplasm, or might be attached to the surface of the endoplasmic reticulum. The endoplasmic reticulum is called the rough endoplasmic reticulum due to the presence of ribosomes on its surface. 
• In simpler words, proteins are the body’s building blocks, made of amino acids. They are created inside ribosomes, which are small structures found in the cytoplasm or attached to the endoplasmic reticulum. When ribosomes are attached to the endoplasmic reticulum, it’s called the rough endoplasmic reticulum because the ribosomes give it a rough surface. 

Page No. 59

Q1. Make a comparison and write down ways in which plant cells are different from animal cells.
Ans:

Q2. How is a prokaryotic cell different from a eukaryotic cell?
Ans:

Q3. What would happen if the plasma membrane ruptures or breaks down?
Ans:

• The plasma membrane is the selectively permeable membrane that surrounds the cell and allows the entry and exit of selected materials of the cell. 
• If it ruptures, the contents of the cell will come in direct contact with the surrounding medium, and not only unwanted material will be able to enter freely into the cell, but useful material will also find its way out of the cell easily. 
• This will seriously disrupt the various metabolic activities of the cell and will result in its imminent death.

Q4. What would happen to the life of a cell if there was no Golgi apparatus?
Ans:

• If there were no Golgi apparatus, the material synthesized by the endoplasmic reticulum would not be carried to the various parts inside and outside of the cell.
  
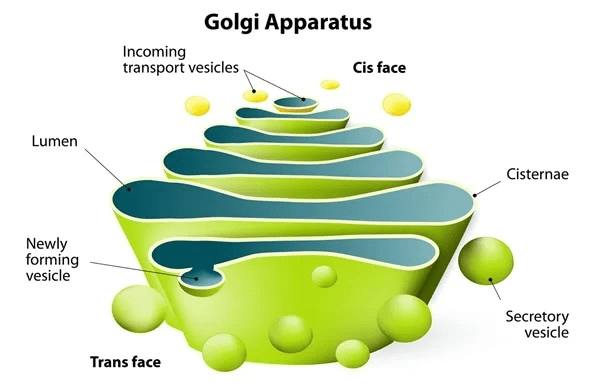
• Also, as the Golgi apparatus performs the function of storage and modification of the material synthesized in the cell, these materials would not be stored and modified further.
• Moreover, there will be no production of lysosomes, which will cause the accumulation of waste material, viz., worn out and dead cell organelles within the cell, which will ultimately lead to cell death.

Q5. Which organelle is known as the powerhouse of the cell? Why
Ans:

• Mitochondria are known as the powerhouse of the cell because these are the sites of cellular respiration.
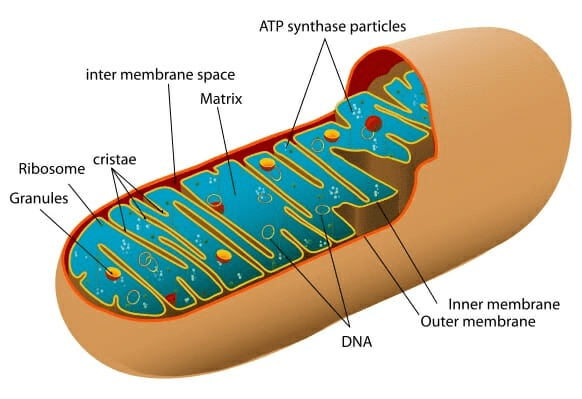  Mitochondria
• The energy that is released by the mitochondria is in the form of ATP molecules and is required for various chemical activities needed for. 
• The energy stored in ATP is used by the body to make new chemical compounds and to perform mechanical work. 
• Thus, mitochondria are known as the powerhouse of cells.

Q6. Where do the lipids and proteins constituting the cell membrane get synthesized?
Ans:

• Lipids and proteins are the essential parts of the plasma membrane, which are synthesized through the endoplasmic reticulum. 
• The endoplasmic reticulum is found to be of two types based on the substances they synthesize. 
• The smooth endoplasmic reticulum is responsible for the synthesis of lipids, while the rough endoplasmic reticulum is responsible for the synthesis of proteins. 

Q7. How does an Amoeba obtain its food?
Ans:

• Amoeba takes in food using temporary finger-like extensions of the cell surface, which fuse over the food particle, forming a food vacuole as shown in the figure. 
• Inside the food vacuole, complex substances are broken down into simpler ones, which then diffuse into the cytoplasm. 
• The remaining undigested material is moved to the surface of the cell and thrown out.
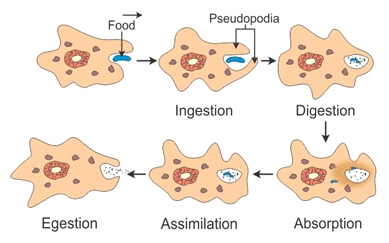  Nutrition in Amoeba

Q8. What is osmosis?
Ans: It is the passage of solvent from a region of high concentration to a region of low concentration through a semipermeable membrane.

Q9. Carry out the following osmosis experiment
Take four peeled potato halves and scoop each one out to make potato cups. One of these potato cups should be made from a boiled potato. Put each potato cup in a trough containing water. Now,
(a) Keep cup A empty.
(b) Put one teaspoon of sugar in cup B
(c) Put one teaspoon salt in cup C
(d) Put one teaspoon of sugar in the boiled potato cup D.
Keep these for two hours. Then observe the four potato cups and answer the following
(i) Explain why water gathers in the hollowed portion of B and C.
(ii) Why is potato A necessary for this experiment?
(iii) Explain why water does not gather in the hollowed-out portions of A and D.
Ans: 
(i) 

• Water gathers in the hollowed portion of cups B and C because of the process of endosmosis (moving in of the solvent). The potato wall acts as a semi-permeable membrane. 
• As cups B and C are filled with sugar and salt, respectively, and their outer part is in contact with the water, the concentration of water outside the cups is higher than inside the cups. 
• So, water moves from its higher concentration towards the lower concentration, i.e., inside the cup. 

(ii) Potato A is necessary for this experiment because:

• Potato A acts as a control of the experiment. It is very necessary to compare the results of the experiment. 
• It shows that if the concentration of water is the same on both sides, there will be no movement of water. 

(iii) Water does not gather in the hollowed-out portions of A and D because:

• Water does not gather in the hollowed-out portions of A as it does not contain a hypertonic solution, so there is no concentration difference and hence no movement of solvent. 
• Water does not gather in cup D as the cells of the boiled potato are dead, and the potato wall is no longer semi-permeable. Hence, no osmosis occurs.

Q10. Which type of cell division is required for the growth and repair of the body and which type is involved in the formation of gametes?
Ans:

• For growth and repair, mitotic division (mitosis) is involved as this type of division keeps the chromosome number constant.
• For gamete formation, meiosis is involved as a reduction of chromosome number is necessary for this case.

Page No. 39

Q1. What are canal rays?
Ans: Canal rays are a type of positively charged radiation discovered by E. Goldstein in 1886. They are produced in a gas discharge and are significant for the following reasons:

• They helped in the identification of protons, a key subatomic particle.
• Canal rays consist of positive ions that move towards the cathode in a discharge tube.
• Their discovery contributed to the understanding of atomic structure.

Goldstein’s experimental setup
Q2. If an atom contains one electron and one proton, will it carry any charge or not?
Ans: No, it will not carry any charge because the number of protons (positively charged) is equal to the number of electrons (negatively charged).

Page No. 41
Q1. On the basis of Thomson’s model of an atom, explain how the atom is neutral as a whole.
Ans: According to Thomson’s model, an atom is made up of a sphere of positive charge with electrons embedded within it. This arrangement is designed to create a stable electrostatic balance.

• The atom is neutral because it contains an equal number of electrons and positively charged particles.
• The positive charge of the sphere balances the negative charge of the electrons.
• Thus, the overall charge of the atom is zero, making it electrically neutral.

Thomson’s Model of an atom

Q2. On the basis of Rutherford’s model of an atom, which subatomic particle is present in the nucleus of an atom?
Ans: According to Rutherford’s model of the atom:

• Protons are present in the nucleus, giving it a positive charge.
• The nucleus contains most of the atom’s mass.
• Neutrons are also found in the nucleus, contributing to the overall mass.

Rutherford’s Model of an atom
Q3. Draw a sketch of Bohr’s model of an atom with three shells.
Ans: 

A line diagram showing different energy levels of energies E₁, E₂ and E₃ for the electrons

Q4. What do you think would be the observation if the α-particle scattering experiment is carried out using a foil of a metal other than gold?
Ans: If the metal taken is heavier than gold, then the deviation shown by α-particles will be more, and if the metal taken is lighter than gold, then the deviation shown will be less due to less repulsion between positively α-particles and nucleus.

Q5. Name the three sub-atomic particles of an atom.
Ans: The three sub-atomic particles of an atom are:
(i) Protons
(ii) Electrons
(iii) Neutrons

Q6. Helium atom has an atomic mass of 4 u and two protons in its nucleus. How many neutrons does it have?
Ans: Number of neutrons = Atomic mass – Number of protons 
For a helium atom:

• Atomic mass = 4 u
• Number of protons = 2
• Therefore, number of neutrons = 4 – 2 = 2

Page No. 42

Q1. Write the distribution of electrons in carbon and sodium atoms.
Ans: 

 (a) Electronic distribution in a carbon atom:

• Atomic number: 6
• Number of electrons: 6
• Distribution: K = 2, L = 4

(b) Distribution of electrons in a sodium atom:

• Atomic number: 11
• Number of electrons: 11
• Distribution: K = 2, L = 8, M = 1

Q2. If K and L shell of an atom are full, then what would be the total number of electrons in the atom?
Ans. The maximum number of electrons in an atom with full K and L shells is:

• K shell: 2 electrons
• L shell: 8 electrons

Therefore, the total number of electrons in the atom is:

• Total: 10 electrons

Page No. 44

Q1. How will you find the valency of chlorine, sulphur and magnesium?
Ans: To find the valency of chlorine, sulphur, and magnesium:

Chlorine (Cl):

• Atomic number: 17
• Electrons: 2, 8, 7
• Can gain 1 electron to achieve stability (like argon).
• Valency: 1

Sulphur (S):

• Atomic number: 16
• Electrons: 2, 8, 6
• Can gain 2 electrons to achieve stability (like argon).
• Valency: 2

Magnesium (Mg):

• Atomic number: 12
• Electrons: 2, 8, 2
• Can lose 2 electrons to achieve stability (like neon).
• Valency: 2

Q2. If number of electrons in an atom is 8 and number of protons is also 8, then 
(i) what is the atomic number of the atom and 
(ii) what is the charge on the atom?
Ans:
(i) The atomic number is equal to the number of protons in an atom. In this case:
Atomic number = Number of protons = 8
(ii)  The charge of an atom is determined by the balance between protons and electrons.

• Since the number of electrons (8) is equal to the number of protons (8), the atom has no overall charge.
• Thus, the charge on the atom is zero.

Q3. With the help of Table 4.1, find out the mass number of oxygen and sulphur atom.

Ans: 
(a) To find the mass number of Oxygen:
Number of protons = 8
Number of neutrons = 8
Atomic number = 8
Atomic mass number = Number of protons + number of neutrons = 8 + 8 = 16
Therefore, mass number of oxygen = 16
(b) To find the mass number of Sulphur:
Number of protons = 16
Number of neutrons = 16
Atomic number = 16
Atomic mass number = Number of protons + number of neutrons = 16 + 16 = 32

Page No. 45

Q1. For the symbol H, D and T tabulate three sub-atomic particles found in each of them.
Ans: 

Hydrogen (H): The most common isotope, consisting of a single proton and no neutrons.

Deuterium (D): A heavier isotope of hydrogen, with one neutron in addition to the proton.

Tritium (T): A radioactive isotope of hydrogen, containing two neutrons and one proton.

Q2. Write the electronic configuration of any one pair of isotopes and isobars.
Ans: 

Isotopes : Isotopes have the same electronic configuration because they have the same number of electrons and protons, differing only in the number of neutrons.
Example : ¹²C₆ and ¹⁴C₆ are isotopes, have the same electronic configuration as (2, 4)

Electronic Configuration(2,4) of Carbon atom

Isobars: Isobars have the same mass number but differ in atomic number, leading to different electronic configurations.

Example :  ²²Ne₁₀ and ²²Na₁₁ are isobars. They have different atomic number but mass number is same. 

Page No. 46, 47 & 48

Q1. Compare the properties of electrons, protons and neutrons.

Ans: ElectronProtonNeutron(a) It is negatively charged.(a) It is positively charged.(a) It is neutral.(b) Its absolute mass is equal to 9.1 x 10^-31 kg. (b) Its absolute mass is equal to 1.673 x 10^-27 kg. (b) Its mass is slightly more than that of protons. Its absolute mass is 1.675 x 10^-27 kg.

Q2. What are the limitations of J.J. Thomson’s model of the atom?
Ans: Limitations of JJ Thomson’s model of an atom:
(i) The results of experiments carried out by other scientists could not be explained by this model
(ii) The positive charge is spread all over could not be justified.

Q3. What are the limitations of Rutherford’s model of the atom?
Ans: Limitations of Rutherford’s model of an atom
(i) According to classical electromagnetic theory, a moving charged particle, such as an electron, under the influence of attractive force, loses energy continuously in the form of radiations. As a result of this, the electron should lose energy and, therefore, should move in even smaller orbits, ultimately falling into the nucleus. But the collapse does not occur. There is no explanation for this behaviour.
(ii) According to Rutherford, the electrons revolve around the nucleus in fixed orbits. However, Rutherford did not specify the number of orbits and the number of electrons in each orbit.

Q4. Describe Bohr’s model of the atom.
Ans: Bohr made a bold new suggestion that particles at the atomic level would behave differently from macroscopic (bigger) objects.
According to Bohr’s theory:

• Electrons travel in specific paths called orbits or energy levels.
• While in these orbits, electrons do not emit energy.
• Electrons can move to a higher energy level when they absorb energy.
• When electrons drop back to a lower energy level, they release energy.

This model helped explain the stability of atoms and their emission spectra.

Bohr’s Model of an atom

Q5. Compare all the proposed models of an atom given in this chapter.
Ans: Thomson modelRutherford modelBohr model(a) The positive charge is spread all over and electrons are embedded in it like seeds in the watermelon. (a) There is a positively charged centre called the nucleus where the mass of the atom is concentrated.(a) Electrons revolve in certain discrete orbits called energy levels.(b ) The positive and negative charges are equal, therefore the atom is neutral.(b) Electrons revolve around the nucleus in well-defined orbits.(b) While revolving in these orbits, electrons do not radiate energy.(c) The nucleus is very small compared to the overall size of the atom.
(c) The size of the nucleus is very small as compared to the size of an atom.(c) These orbits are represented by K, L, M, N or 1, 2, 3, 4.

Q6. Summarize the rules for writing of distribution of electrons in various shells for the first eighteen elements.
Ans: The distribution of electrons in the shells of an atom is known as electronic configuration. To write the electronic configuration for an element, follow these steps:

• Determine the total number of electrons using the element’s atomic number.
• Distribute these electrons across the shells in order of increasing energy, following the 2n² rule.
• Fill the shell with the lowest energy first, then proceed to the next higher energy shells.
• List the number of electrons in each shell, starting from the lowest, separated by commas. For example, sodium (atomic number 11) has:

Electronic configuration of Na: K = 2, L = 8, M = 1 

The maximum number of electrons in different shells is:

• K-shell (1st shell) = 2
• L-shell (2nd shell) = 8
• M-shell (3rd shell) = 18
• N-shell (4th shell) = 32

Key points to remember:

• The outermost shell can hold a maximum of 8 electrons.
• Electrons fill shells in a step-wise manner; inner shells must be filled before outer shells.

Q7. Define valency by taking examples of silicon and oxygen.
Ans: The valency of an atom is the number of hydrogen atoms which combine with one atom of an element.
For example, 

• Silicon (atomic number 14) has the following electronic distribution:
  K = 2, L = 8, M = 4.
  In the outermost shell, there are 4 electrons; hence, one atom of silicon will combine with 4 atoms of hydrogen. So, the valency of silicon is 4.
• In the case of oxygen (atomic number 8), the electronic distribution in various shells is given below:
  K = 2, L = 6
  There are six valence electrons in the atom of oxygen. So, one atom of oxygen will combine with 2 atoms of hydrogen to make a noble gas configuration. Hence, the valency of oxygen is 2.

Q8. Explain with examples (i) Atomic number, (ii) Mass number, (iii) Isotopes and (iv) Isobars. Give any two uses of isotopes.
Ans: 
(i) Atomic number: The atomic number of an atom is equal to the number of protons in the nucleus of an atom.
Atomic number = Number of protons.
(ii) Mass number: The total mass of the atom is due to the sum of the masses of protons and neutrons present in the nucleus. The mass number of an atom is equal to the sum of the number of protons and neutrons in the nucleus.
Mass number = Number of protons + Number of neutrons.
(iii) Isotopes: Isotopes are the atoms of the same element having the same atomic number but different mass numbers. For example, Hydrogen has three isotopes: protium (1), deuterium (2), and tritium (3).
(iv) Isobars: Isobars are the atoms of the different elements having the same mass number and different atomic numbers. For example, Calcium (atomic number 20) and argon (atomic number 18) both have a mass number of 40.

Uses of isotopes:
(i) Cobalt-60 is a radioactive isotope of cobalt. It is used in radiotherapy for cancer.
(ii) ¹⁴C is a radioactive isotope of carbon. It is used in carbon dating.

Q9. Na⁺  has completely filled K and L shells. Explain.
Ans: Sodium has the atomic number 11. It has 11 electrons in its orbitals, wherein the number of protons is equal to the number of electrons. Hence, its electronic configuration is K-2, L-8, and M-1. The one electron in the M shell is lost, and it obtains a positive charge since it has one more proton than electrons and obtains a positive charge, Na⁺. Na⁺ is formed when one electron is lost by a sodium atom, as given below:

The new electronic configuration is K-1; L-8 which is the filled state. Hence it is very difficult to eliminate the electron from a filled state as it is very stable.

Q10. If bromine atom is available in the form of, say, two isotopes  ⁷⁹Br₃₅ (49.7%) and ⁸¹Br₃₅ (50.3%) calculate the average atomic mass of bromine atom.
Ans: Average atomic mass of Br
= ( (79 x 49.7) + (81 x 50.3) ) / 100
= (3926.3 + 4074.3) / 100
= 8000.6 / 100
= 80.006 u

Q11. The average atomic mass of a sample of an element X is 16.2 u. What are the percentages of isotopes  in the sample?
Ans: It is given that the average atomic mass of the sample of element X is 16.2 u.
Let the percentage of isotope 18 / 8 X be y%. Thus, the percentage of isotope 16 / 8 X will be (100 – y) %.
Therefore,
18 x (y/100) + 16 x ((100-y)/100) = 16.2
18y/100 + ( 16(100 – y) / 100 ) = 16.2
(18y+1600-16y )/100 = 16.2
18y + 1600 – 16y = 1620
2y + 1600 = 1620
2y = 1620 – 1600
y = 10
Therefore, the percentage of isotope 18 / 8 X is 10%.
And, the percentage of isotope 16 / 8 X is (100 – 10) % = 90%.

Q12. If Z = 3, what would be the valency of the element? Also, name the element.
Ans. Z = 3
Electronic configuration is 2, 1.
Valence electron is equal to 1.
Valency is also equal to 1.
The name of the element is lithium.

Q13. Composition of the nuclei of two atomic species X and Y are given as under

Give the mass numbers of X and Y. What is the relation between the two species?
Ans: Mass number of X = 6 + 6 = 12 
Mass number of Y = 6 + 8 = 14
Atomic number of X = 6 
Atomic number of Y = 6
X and Y are isotopes since both the elements have same atomic number but different mass number.

Q14. For the following statements, write T for ‘True’ and F for ‘False’.
(a) J.J. Thomson proposed that the nucleus of an atom contains only nucleons.
(b) A neutron is formed by an electron and a proton combining together. Therefore, it is neutral.
(c) The mass of an electron is about 1 / 2000 times that of proton.
(d) An isotope of iodine is used for making tincture iodine, which is used as a medicine.
Ans. (a) False (b) False (c) True (d) False

Q15. Rutherford’s alpha-particle scattering experiment was responsible for the discovery of
(a) Atomic nucleus
(b) Electron
(c) Proton
(d) Neutron
Ans: (a) Atomic nucleus
An atomic nucleus is the dense central core of an atom, composed of protons and neutrons held together by the strong nuclear force.

Q16. Isotopes of an element have
(a) the same physical properties
(b) different chemical properties
(c) different number of neutrons
(d) different atomic numbers
Ans: (c) different number of neutrons

Q17. Number of valence electrons in Cl ^–ion are:
(a) 16
(b) 8
(c) 17
(d) 18
Ans: (b) 8
Cl^– has 8 valence electrons. Cl^– has 17 + 1 = 18 electrons. Its electronic configuration is 2, 8, 8.

Q18. Which one of the following is a correct electronic configuration of sodium?
(a) 2, 8
(b) 8, 2, 1
(c) 2, 1, 8
(d) 2, 8, 1
Ans: (d)  2 ,8 ,1 
2 ,8 ,1 is the correct electronic configuration of sodium.

Q19. Complete the following table.

Ans: 
Atomic number(Z) =Number of protons
Mass number = Number of neutrons + atomic number
=> Mass number(A) = Number of neutrons + number of neutrons

Page No. 27

Q1. In a reaction, 5.3 g of sodium carbonate reacted with 6 g of ethanoic acid. The products were 2.2 g of carbon dioxide, 0.9 g water and 8.2 g of sodium ethanoate. Show that these observations are in agreement with the law of conservation of mass.
Sodium carbonate ethanoic acid → sodium ethanoate carbon dioxide water
Ans: 

Mass of reactants = 5.3 g + 6 g = 11.3 g
Mass of products = 2.2 g + 0.9 g + 8.2 g = 11.3 g
Mass of reactants = Mass of products
Therefore, the law of conservation of mass is proven.

Q2. Hydrogen and oxygen combine in the ratio of 1 : 8 by mass to form water. What mass of oxygen gas would be required to react completely with 3g of hydrogen gas?
Ans: Since hydrogen and oxygen combine in the ratio of 1:8 by mass, 3g of hydrogen gas will react completely with 24 g of oxygen gas.

Q3. Which postulate of Dalton’s atomic theory is the result of the law of conservation of mass?
Ans: Dalton’s postulate that “atoms can neither be created nor destroyed,” is a result of the law of conservation of mass.

Q4. Which postulate of Dalton’s atomic theory can explain the law of definite proportions?
Ans: Atoms combine in a fixed ratio to form compounds, which can explain the law of definite proportions.Page No. 30

Q1. Define atomic mass unit.
Ans: It is defined as equal to 1/12th of the mass of 1 atom of C-12. It is called unified mass denoted by ‘u’ these days.

Q2. Why is it not possible to see an atom with naked eyes?
Ans: The size of an atom is so small that it is not possible to see it with naked eyes. Also, the atom of an element does not exist independently.Page No. 34

Q1. Write down the formulae of 
(a) sodium oxide
(b) aluminium chloride
(c) sodium sulphide
(d) magnesium hydroxide
Ans:
(a) Formula of Sodium Oxide

(b) Formula of Aluminium Chloride

(c) Formula of Sodium Sulphide

(d) Formula of Magnesium Hydroxide

Q2. Write down the names of compounds represented by the following formulae:
(a) Al₂(SO₄)₃
(b) CaCl₂
(c) K₂SO₄
(d) KNO₃
(e) CaCO₃
Ans: 
(a) Aluminium sulphate 
(b) Calcium chloride 
(c) Potassium sulphate 
(d) Potassium nitrate 
(e) Calcium carbonate

Q3. What is meant by the term chemical formula?
Ans: The chemical formula of a compound is a symbolic representation of its composition.
Chemical Formula of Water

Q4. How many atoms are present in 
(a) H₂S molecule and
(b) PO₄^3- ion?
Ans: 
(i) H₂S molecule has 2 atoms of hydrogen and 1 atom of sulphur hence 3 atoms in totality.
(ii) PO₄^3- ion has 1 atom of phosphorus and 4 atoms of oxygen hence 5 atoms in totality.Page No. 35

Q1. Calculate the molecular masses of H₂, O₂, Cl₂, CO₂, CH₄, C₂H₆, C₂H₄, NH₃, CH₃OH.
Ans: 
Molecular mass of H₂ = 2 × Atomic mass of H
= 2 × 1
= 2 u
Molecular mass of O₂ = 2 × Atomic mass of O
= 2 × 16
= 32 u
Molecular mass of Cl₂ = 2 × Atomic mass of Cl
= 2 × 35.5
= 71 u
Molecular mass of CO₂ = Atomic mass of C₂ × Atomic mass of O
= 12+ (2+16) = (12 + 32)u 
= 44 u
Molecular mass of CH₄= Atomic mass of C4 × Atomic mass of H
= 12+ (4 x 1)u = (12 + 4)u 
= 16 u
Molecular mass of C₂H₆ = 2× Atomic mass of C₆× Atomic mass of H
= (2 x 12 + 6 x 1)u = (24 + 6)u 
= 30 u
Molecular mass of C₂H₄ = 2 x Atomic mass of C₄ × Atomic mass of H
= (2 x 12 + 4 x 1)u = (24 + 4)u 
= 28 u
Molecular mass of NH₃ = Atomic mass of N₃ × Atomic mass of H
= (14 + 3 x 1)u = (14 + 3)u 
= 17 u
Molecular mass of CH₃OH = Atomic mass of C₃ × Atomic mass of H Atomic mass of O Atomic mass of H
= (12 + 3 x 1 + 16 + 1)u = (12 + 3 + 17)u 
= 32 u

Q2. Calculate the formula unit masses of ZnO, Na₂O, K₂CO₃, given atomic masses of Zn = 65 u, Na = 23 u, K = 39 u, C = 12 u, and O = 16 u.
Ans:
(i) Formula unit mass of ZnO 
= 65 + 16 = 81 u 
(ii) Formula unit mass of Na₂O
= 2 x 23 + 16 = 46 + 16 = 62 u
(iii) Formula unit mass of K₂CO₃ 
= 2 x 39 + 12 + 3 x 16
= 78 + 12 + 48 = 138 uPage No. 36

Q1. A 0.24 g sample of a compound of oxygen and boron was found by analysis to contain 0.096 g of boron and 0.144 g of oxygen. 
Calculate the percentage composition of the compound by weight.
Ans: Percentage of boron = (mass of boron / mass of the compound) x 100
= (0.096g / 0.24g) x 100  
= 40%
Percentage of oxygen = 100 – percentage of boron
= 100 – 40 
= 60%

Q2. When 3.0 g of carbon is burnt in 8.00 g oxygen, 11.00 g of carbon dioxide is produced. What mass of carbon dioxide will be formed when 3.00 g of carbon is burnt in 50.00 g of oxygen? Which law of chemical combination will govern your answer?
Ans:  When 3.0 g of carbon is burnt in 8.00 g of oxygen, 11.00 g of carbon dioxide is produced.
Given that
3.0 g of carbon combines with 8.0 g of oxygen to give 11.0 of carbon dioxide.
Find out
We need to find out the mass of carbon dioxide that will be formed when 3.00 g of carbon is burnt in 50.00 g of oxygen.
Solution
First, let us write the reaction taking place here.
C + O₂ → CO₂
As per the given condition, when 3.0 g of carbon is burnt in 8.00 g of oxygen, 11.00 g of carbon dioxide is produced.
3g + 8g →11 g ( from the above reaction)
The total mass of reactants = mass of carbon + mass of oxygen
= 3g+8g
= 11g
The total mass of reactants = Total mass of products
Therefore, the law of conservation of mass is proved.
Then, it also depicts that carbon dioxide contains carbon and oxygen in a fixed ratio by mass, which is 3:8.
Thus, it further proves the law of constant proportions.
3 g of carbon must also combine with 8 g of oxygen only.
This means that (50−8) = 42g of oxygen will remain unreacted.
The remaining 42 g of oxygen will be left un-reactive. In this case, too, only 11 g of carbon dioxide will be formed.
The above answer is governed by the law of constant proportions.

Q3. What are polyatomic ions? Give examples.
Ans: Polyatomic ions are ions that contain more than one atom, but they behave as a single unit.
Example: CO₃^2-, H₂PO₄^– 

Q4. Write the chemical formulae of the following.
(a) Magnesium chloride
(b) Calcium oxide
(c) Copper nitrate
(d) Aluminium chloride
(e) Calcium carbonate.
Ans: The following are the chemical formula of the above-mentioned list:
(a) Magnesium chloride – MgCl₂
(b) Calcium oxide – CaO
(c) Copper nitrate – Cu(NO₃)₂
(d) Aluminium chloride – AlCl₃
(e) Calcium carbonate – CaCO₃

Q5. Give the names of the elements present in the following compounds.
(a) Quick lime
(b) Hydrogen bromide
(c) Baking powder
(d) Potassium sulphate.
Ans:  The following are the names of the elements present in the following compounds:
(a) Quick lime – Calcium and oxygen (CaO)
(b) Hydrogen bromide – Hydrogen and bromine (HBr)
(c) Baking powder – Sodium, Carbon, Hydrogen, Oxygen (NaHCO₃)
(d) Potassium sulphate – Sulphur, Oxygen, Potassium (K₂SO₄)

Q6. Calculate the molar mass of the following substances.
(a) Ethyne, C₂H₂ 
(b) Sulphur molecule, S₈ 
(c) Phosphorus molecule, P₄ (Atomic mass of phosphorus =31)
(d) Hydrochloric acid, HCl
(e) Nitric acid, HNO₃
Ans:  Listed below is the molar mass of the following substances:
(a) Molar mass of Ethyne C₂H₂= 2 x Mass of C+2 x Mass of H = (2×12)+(2×1)=24+2=26g
(b) Molar mass of Sulphur molecule S₈ = 8 x Mass of S = 8  x 32 = 256g
(c) Molar mass of Phosphorus molecule, P₄ = 4 x Mass of P = 4 x 31 = 124g
(d) Molar mass of Hydrochloric acid, HCl = Mass of H+ Mass of Cl = 1+35.5 = 36.5g
(e) Molar mass of Nitric acid, HNO₃ =Mass of H+ Mass of Nitrogen + 3 x Mass of O = 1 + 14+
3×16 = 63g

Page No. 15

Q1. What is meant by a substance?
Ans: A pure substance is one that is made up of only one kind of particle, either atoms or molecules. It has definite composition and distinct properties.  Examples of Pure SubstancesA pure substance consists of only one type of particle, either atoms or molecules. It has a definite composition and distinct properties. Examples include:

• Oxygen
• Carbon

In contrast, a mixture contains two or more pure substances. For instance:

• Sea water is a mixture of salt and water.
• Soil contains various organic and inorganic materials.

Key points about mixtures:

• Mixtures can be separated into their components through physical processes.
• Each component retains its own properties.

Types of mixtures include:

• Homogeneous mixtures have a uniform composition (e.g., sugar in water).
• Heterogeneous mixtures have a non-uniform composition (e.g., sand and salt).

In summary, a pure substance has consistent properties, while a mixture contains multiple substances that can vary in composition.

Q2. List the points of differences between homogeneous and heterogeneous mixtures.

Ans:

Page No. 18

Q1. Differentiate between homogeneous and heterogeneous mixtures with examples.
Ans: The following are the differences between heterogeneous and homogenous mixtures.

Q2. How are sol, solution and suspension different from each other?
Ans:

Q3. To make a saturated solution, 36g of sodium chloride is dissolved in 100 g of water at 293 K. Find its concentration at this temperature.

Ans: Mass of solute (NaCl): 36 g

Mass of solvent (H₂O): 100 g

Mass of solution: 136 g (NaCl + H₂O)

Concentration: Calculated as follows:

• Concentration = (Mass of solute / Mass of solution) × 100
• Concentration = (36 g / 136 g) × 100
• Concentration = 26.47%

Thus, the concentration of the solution is 26.47%.Page No. 19

Q1. Classify the following as chemical or physical changes: 

• cutting of trees, 
• melting of butter in a pan, 
• rusting of almirah, 
• boiling of water to form steam, 
• passing of electric current, through water and the water breaking down into hydrogen and oxygen gases, 
• dissolving common salt in water, 
• making a fruit salad with raw fruits, and
• burning of paper and wood.

Ans: The following is the classification into physical and chemical change:

Q2. Try segregating the things around you as pure substances or mixtures.
Ans: Listed below are the classifications based on pure substances and mixtures:
 Page No. 22

Exercises

Q1. Which separation techniques will you apply for the separation of the following? 
(a) Sodium chloride from its solution in water. 
(b) Ammonium chloride from a mixture containing sodium chloride and ammonium chloride. 
(c) Small pieces of metal in the engine oil of a car. 
(d) Different pigments from an extract of flower petals.
(e) Butter from curd.
(f) Oil from water. 
(g) Tea leaves from tea.
(h) Iron pins from sand. 
(i) Wheat grains from husk. 
(j) Fine mud particles suspended in water.
Ans: (a) In water, sodium chloride in its solution can be separated through the process of evaporation (as well as crystallization). 
(b) The sublimation technique is appropriate as ammonium chloride supports sublimation. 
(c) Tiny metal pieces in the engine oil of a car can be filtered manually.
(d) Chromatography can be used to separate different pigments from an extract of flower petals.
(e) The technique of churning can be applied to separate butter from curd. It is based on the concept of difference in density. 
(f) To separate oil from water, which are two immiscible liquids which vary in their densities, using a funnel can be an effective method. 
(g) Tea leaves can be manually separated from tea using simple filtration methods. 
(h) Iron pins can be separated from sand either manually or with the use of magnets as the pins exhibit strong magnetic quality, which can be a key characteristic taken into consideration. 
(i) The differentiating property between husk and wheat is that there is a difference in their mass. If treated with a small amount of wind energy, a remarkable variation in the moving distance is noticed. Hence, to separate them, the sedimentation/winnowing procedure can be applied. 
(j) Due to the property of water, sand or fine mud particles tend to sink in the bottom as it is denser, provided they are undisturbed. Through the process of sedimentation/decantation, water can be separated from fine mud particles, as the technique is established on obtaining clear water by tilting it out.Page No. 23

Q2. Write the steps you would use for making tea. Use the words solution, solvent, solute, dissolve, soluble, insoluble, filtrate and residue.
Ans:  Steps for Making Tea

• Heat a cup of milk, which acts as the solvent.
• Add tea powder or leaves, the solute, to the boiling milk.
• Observe that the tea powder remains insoluble while boiling.
• Add sugar to the boiling solution and stir.
• Sugar, being a solute, is soluble in the milk.
• Continue stirring until the sugar completely dissolves, achieving saturation.
• Once the raw smell of tea leaves disappears, remove the solution from heat.
• Filter the mixture to separate the tea powder, which becomes the residue.
• The liquid that passes through is the filtrate, containing the dissolved sugar and milk.

Q3. Pragya tested the solubility of three different substances at different temperatures and collected the data as given below (results are given in the following table, as grams of substance dissolved in 100 grams of water to form a saturated solution).

(a) What mass of potassium nitrate would be needed to produce a saturated solution of potassium nitrate in 50 grams of water at 313 K? 
(b) Pragya makes a saturated solution of potassium chloride in water at 353 K and leaves the solution to cool at room temperature. What would she observe as the solution cools? Explain. 
(c) Find the solubility of each salt at 293 K. Which salt has the highest solubility at this temperature? 
(d) What is the effect of change of temperature on the solubility of a salt?
Ans: (a) Given:
Mass of potassium nitrate required to produce a saturated solution in 100 g of water at 313 K = 62g
To find:
Mass of potassium nitrate required to produce a saturated solution in 50 g of water =?
Required amount = 62 x 50/100 = 31
Hence, 31 g of potassium nitrate is required.
(b) The solubility of potassium chloride in water is decreased when a saturated solution of potassium chloride loses heat at 353 K. Consequently, Pragya would observe crystals of potassium chloride, which would have surpassed its solubility at low temperatures.
(c) As per the given data, that is
Solubility of potassium nitrate at 293K = 32 g
Solubility of sodium chloride at 293K = 36 g
Solubility of potassium chloride at 293K = 35 g
Solubility of ammonium chloride at 293K = 37g
We can observe from this data that ammonium chloride has the highest solubility at 293K.
(d) Effect of change of temperature on the solubility of salts:
The table clearly depicts that the solubility of the salt is dependent upon the temperature and increases with an increase in temperature. With this, we can infer that when a salt arrives at its saturation point at a specific temperature, there is a propensity to dissolve more salt through an increase in the temperature of the solution.

Q4. Explain the following, giving examples. 
(a) Saturated solution 
(b) Pure substance 
(c) Colloid 
(d) Suspension
Ans: (a) Saturated solution: It is the state in a solution at a specific temperature when a solvent is no longer soluble without an increase in temperature. Example: Excess carbon leaves off as bubbles from a carbonated water solution saturated with carbon.
(b) Pure substance: A substance is said to be pure when it comprises only one kind of molecule, atom or compound without adulteration with any other substance or any divergence in the structural arrangement. Examples: Sulphur, diamonds etc.
(c) Colloid: A Colloid is an intermediate between solution and suspension. It has particles of various sizes that range between 2 to 1000 nanometers. Colloids can be distinguished from solutions using the Tyndall effect. Tyndall effect is defined as the scattering of light (light beam) through a colloidal solution. Examples: Milk and gelatin.
(d) Suspension: It is a heterogeneous mixture that comprises solute particles that are insoluble but are suspended in the medium. These particles that are suspended are not microscopic but visible to bare eyes and are large enough (usually larger than a micrometer) to undergo sedimentation.

Q5. Classify each of the following as a homogeneous or heterogeneous mixture. 
soda water, wood, air, soil, vinegar, filtered tea.
Ans: The following is the classification of the given substances into homogenous and heterogenous mixtures.

Q6. How would you confirm that a colorless liquid given to you is pure water?
Ans: We can confirm if a colorless liquid is pure by setting it to boil. If it boils at 100°C, it is said to be pure. But if there is a decrease or increase in the boiling point, we infer that water has added impurities and, hence not pure.Page No. 24

Q7. Which of the following materials fall in the category of a “pure substance”? 
(a) Ice 
(b) Milk
(c) Iron 
(d) Hydrochloric acid 
(e) Calcium oxide 
(f) Mercury 
(g) Brick 
(h) Wood 
(i) Air
Ans: The following substances from the above-mentioned list are pure substances:

• Iron
• Ice
• Hydrochloric acid
• Calcium oxide
• Mercury

Q8. Identify the solutions among the following mixtures.
(a) Soil
(b) Seawater
(c) Air
(d) Coal
(e) Soda water
Ans: The following are the solutions from the above-mentioned list of mixtures:

• Sea water
• Air
• Soda water

Q9. Which of the following will show the “Tyndall effect”?
(a) Salt solution
(b) Milk
(c) Copper sulphate solution
(d) Starch solution
Ans:  Milk and starch solution demonstrate the Tyndall effect because they are colloidal solutions. In these solutions, light is scattered, making its path visible.

• The Tyndall effect occurs when light passes through a colloid.
• Colloidal solutions contain particles that are small enough to scatter light.
• Examples of colloids include milk and starch solutions.

Q10. Classify the following into elements, compounds, and mixtures. 
(a) Sodium 
(b) Soil 
(c) Sugar solution 
(d) Silver 
(e) Calcium carbonate 
(f) Tin 
(g) Silicon 
(h) Coal 
(i) Air 
(j) Soap 
(k) Methane 
(i) Carbon dioxide 
(m) Blood
Ans:
 

Q11. Which of the following are chemical changes? 
(a) Growth of a plant 
(b) Rusting of iron 
(c) Mixing of iron filings and sand 
(d) Cooking of food 
(e) Digestion of food 
(f) Freezing of water 
(g) Burning of a candle
Ans: Among the options listed, the following are considered chemical changes:

• Rusting of iron
• Cooking of food
• Digestion of food
• Burning of a candle

The growth of a plant is a complex process involving both chemical and physical changes, while mixing iron filings and sand and freezing water are not chemical changes.

Page No. 3

Q1. Which of the following are matter?
Chair, air, love, smell, hate, almonds, thought, cold, lemon water, the smell of perfume.
Ans: The following substances are matter: Chair, Air, Almonds, Lemon water, and the smell of perfume (The smell is caused by volatile substances which are matter, as they occupy space and have mass).

Matter around us

Q2. Give reasons for the following observation.
The smell of hot sizzling food reaches you several meters away, but to get the smell from cold food, you have to go close.
Ans: When the air is heated, the particles in it gain more kinetic energy and move faster. This is why the smell of hot food travels farther, allowing a person to sense it even from several meters away.

Q3. A diver is able to cut through water in a swimming pool. Which property of matter does this observation show?
Ans: The particles of every matter have a force of attraction between them. This force keeps the particles together in a matter. In the case of water, the force of attraction between particles is less in comparison to solids. Thus, water molecules flow easily, giving way to a diver.

Showing less intermolecular force between liquid molecules.

Q4. What are the characteristics of the particles of matter?
Ans:  The characteristics of particles of matter are:
(i) Presence of intermolecular spaces between particles.
(ii) Particles are in constant motion.
(iii) They attract each other.Page No. 6

Q1. The mass per unit volume of a substance is called density. 
(density=mass/volume). Arrange the following in the order of increasing density – air, exhaust from the chimneys, honey, water, chalk, cotton and iron.
Ans: The following substances are arranged in increasing density: Air < Exhaust from chimney <  Cotton < Water <  Honey < Chalk < Iron.

Q2. (a) Tabulate the differences in the characteristics of states of matter.
(b) Comment upon the following: rigidity, compressibility, fluidity, filling a gas container, shape, kinetic energy and density.
Ans:  (a) The differences in the characteristics of the three states of matter solid, liquid and gas are:-

(b)
(i) Rigidity: It is the property of matter that continues to remain in its shape when treated with an external force.
(ii) Compressibility: Particles have the ability to reduce their intermolecular space when an external force is applied, which increases their density. This characteristic is called compressibility.
(iii) Fluidity: It is the ability of a substance to flow or move about freely.
(iv) Filling the gas container: The particles in a container take their shape as they randomly vibrate in all possible directions.
(v) Shape: It is the definite structure of an object within an external boundary.
(vi) Kinetic energy: Motion allows particles to possess energy, which is referred to as kinetic energy. The increasing order of kinetic energy possessed by various states of matter is Solids < Liquids < Gases.
Mathematically, it can be expressed as K.E = 1/2 mv², where ‘m’ is the mass and ‘v’ is the velocity of the particle.
(vii) Density: It is the mass of a unit volume of a substance. It is expressed as d = M/V, where ‘d’ is the density, ‘M’ is the mass and ‘V’ is the volume of the substance

Q3. Give reasons 
(a) A gas fills completely the vessel in which it is kept. 
(b) A gas exerts pressure on the walls of the container.
(c) A wooden table should be called a solid. 
(d) We can easily move our hand in the air, but to do the same through a solid block of wood, we need a karate expert.
Ans: 
(a) There is a low force of attraction between gas particles. The particles in the filled vessel are free to move about.
(b) Gaseous particles have the weakest attraction force and move randomly in all directions. When a gas particle hits the walls of its container, it applies a force, creating pressure on the walls.
(c) The hardwood table has a clear shape and volume. The wood particles are tightly packed and do not change to fit the shape of a container. This gives the table its solid properties.
(d) The air particles are spread far apart with a lot of space between them, which is why we can move our hands freely through the air. However, in a solid block, the particles are held tightly together by a strong force of attraction, leaving little or no space between them. That’s why breaking a solid block would require the strength of a karate expert.

Q4. Liquids generally have lower density as compared to solids. But you must have observed that ice floats on water. Find out why?
Ans: 

• The mass per unit volume of a substance is called density (density = mass/volume). 
• As the volume of a substance increases, its density decreases. In general, solids have higher density than liquids. Water is also a liquid, so it should also have less density than that of a solid, which is ice.
• Though ice is solid, it has a cage-like structure; hence, there are a large number of empty spaces between its particles. These spaces are larger than the spaces between the particles of water. Thus, for a given mass of water, the volume of ice is greater than that of water.
• Hence, the density of ice is less than that of water. A substance with a lower density than water can float on water. Therefore, ice floats on water.

Page No. 9

Q1. Convert the following temperature to Celsius scale:
(a) 300 K 
(b) 573 K
Ans: To convert a temperature from the Kelvin scale to the Celsius scale, you simply subtract 273 from the given Kelvin temperature.

(a)  (300 – 273)°C = 27°C
(b) (573 – 273)°C = 300°C

Q2. What is the physical state of water at:
(a) 250°C 
(b) 100°C
Ans: 
(a) At 250°C, the physical state of water is gas as the temperature is beyond its boiling point.
(b) At 100°C, it is in the transition state (both liquid and gaseous states) as the water is at its boiling point. Hence, it would be present in both liquid and gaseous state.

Q3. For any substance, why does the temperature remain constant during the change of state?
Ans: It is due to the latent heat as the heat supplied to increase the temperature of the substance is used up to transform the state of matter of the substance; hence, the temperature stays constant. Latent heat is the heat energy needed to change a substance from one form to another without changing its temperature. For example, when ice melts into water, it absorbs heat (latent heat of fusion) without increasing in temperature. Similarly, when water evaporates into steam, it also absorbs heat (latent heat of vaporization) without a temperature change.

Q4. Suggest a method to liquefy atmospheric gases.
Ans: To transform a gas into a liquid, it is necessary to bring its constituent particles or molecules closer. This can be achieved with atmospheric gases by either increasing the pressure or lowering the temperature. Page No. 10

Q1. Why does a desert cooler cool better on a hot dry day?
Ans: A desert cooler works better on hot, dry days because the high temperature and low humidity increase the rate of evaporation. This greater evaporation results in more effective cooling.

Q2. How does the water kept in an earthen pot (matka) become cool during summer?
Ans: An earthen pot has tiny pores that allow water to seep through and evaporate from its surface. This evaporation requires energy, which is drawn from the water inside the pot, making the water cooler.

Q3. Why does our palm feel cold when we put some acetone or petrol or perfume on it?
Ans: Acetone, petrol, and perfume are highly volatile substances. When applied to our palm, they evaporate quickly, absorbing heat from the skin and making our palm feel cold.

Q4. Why are we able to sip hot tea or milk faster from a saucer rather than a cup?
Ans: A saucer has a larger surface area than a cup, which allows for faster evaporation. This rapid evaporation cools the tea or milk more quickly, enabling us to sip it faster.

Q5. What type of clothes should we wear in summer?
Ans: In summer, it is advisable to wear light-colored cotton clothes. Light colors reflect heat, and cotton is breathable, allowing sweat to evaporate and providing a cooling effect on the skin.

Exercises 

Q1. Convert the following temperature to Celsius scale.
(a) 293K 
(b) 470K
Ans: To convert a temperature from the Kelvin scale to the Celsius scale, you simply subtract 273 from the given Kelvin temperature because 0°C=273K.
(a) 293K= (293 – 273)°C = 20°C
(b) 470K= (470 – 273)°C = 197°C

Q2. Convert the following temperatures to the kelvin scale.
(a) 25°C 
(b) 373°C
Ans: 
0°C = 273K
(a) 25°C = (25+273)K = 298K
(b) 373°C = (373+273)K = 646K

Q3. Give reason for the following observations:
(a) Naphthalene balls disappear with time without leaving any solid.
(b) We can get the smell of perfume sitting several metres away.
Ans: 
(a) At room temperature, naphthalene balls undergo sublimation, which means they change directly from a solid to a gaseous state without undergoing the intermediate state, i.e., the liquid state.

Naphthalene Balls

(b) It is because perfumes contain a volatile organic solvent that can easily diffuse through air and, hence, carry the fragrance to people sitting several metres away.

Q4. Arrange the following substances in increasing order of forces of attraction between the particles— water, sugar, oxygen.
Ans: Oxygen (gas) < Water (liquid) < Sugar (solid)

Q5. What is the physical state of water at: 
(a) 25°C, (b) 0°C, (c) 100°C?
Ans: The physical state of water at different temperatures is as follows:
(a) At 25°C, water is in a liquid state (typical room temperature).
(b) At 0°C, water is at its freezing point, so both solid (ice) and liquid (water) phases can be observed.
(c) At 100°C, water is at its boiling point, resulting in the presence of both liquid water and gaseous water (water vapor).

Q6. Give two reasons to justify.
(a) Water at room temperature is a liquid.
(b) An iron almirah is a solid at room temperature.
Ans:

(a) Water remains in a liquid state at room temperature for two main reasons:

1. Its melting or freezing point is lower than room temperature, while its boiling point is higher (100°C).
2. Water has no fixed shape and flows to take the shape of its container, which indicates that it occupies a fixed volume but does not have a defined shape.

(b) An iron almirah is a solid at room temperature for the following reasons:

1. Both the melting and boiling points of iron are above room temperature, meaning it remains solid under these conditions.
2. An iron almirah is rigid and maintains a definite shape, and metals typically have a high density, further confirming that it is solid at room temperature.

Q7. Why is ice at 273 K more effective in cooling than water at the same temperature?
Ans: At 273 K, ice will absorb heat energy or latent heat from the medium during melting to transform into water. As a result, ice has a greater cooling impact than water at the same temperature since water does not absorb the excess heat from the medium.

Q8. What produces more severe burns, boiling water or steam?
Ans: Steam produces severe burns. It is because it is an exothermic reaction that releases a high amount of heat, which it consumes during vaporization.

Q9. Name A, B, C, D, E and F in the following diagram showing change in its state.

Ans: Interconversion of three states of matter: Using temperature or pressure, any state of matter can be turned into another.
(A) Solid to Liquid → Melting (or) fusion (or) liquefaction
(B) Liquid to Gas → Evaporation (or) vaporization
(C) Gas to liquid → Condensation
(D) Liquid to Solid → Solidification
(E) Solid to Gas → Sublimation
(F) Gas to Solid → Deposition