Text Book Solutions All Class

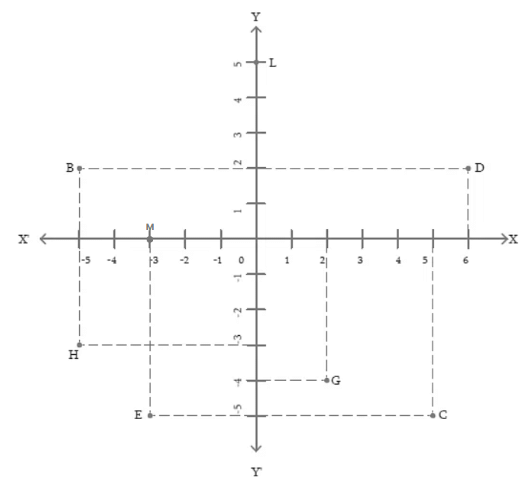
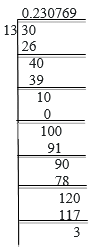
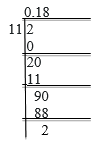
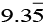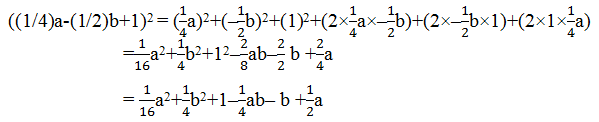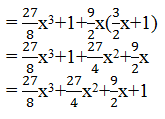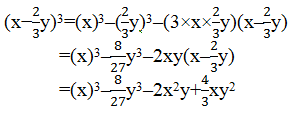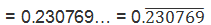Exercise 7.1

Q1. In quadrilateral ACBD, AC = AD and AB bisects ∠ A. Show that ∆ ABC ≅ ∆ ABD. What can you say about BC and BD?

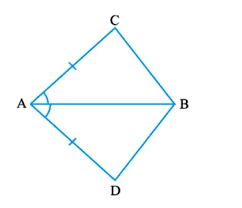
Ans: It is given that AC and AD are equal i.e. AC = AD and the line segment AB bisects ∠A.
We will have to now prove that the two triangles ABC and ABD are similar i.e. ΔABC ≅ ΔABD
Proof:
Consider the triangles ΔABC and ΔABD,
(i) AC = AD (It is given in the question)
(ii) AB = AB (Common
(iii) ∠CAB = ∠DAB (Since AB is the bisector of angle A)
So, by SAS congruency criterion, ΔABC ≅ ΔABD.
For the 2^nd part of the question, BC and BD are of equal lengths by the rule of C.P.C.T.

Q2. ABCD is a quadrilateral in which AD = BC and ∠ DAB = ∠ CBA. Prove that
(i) ∆ ABD ≅ ∆ BAC
(ii) BD = AC 
(iii) ∠ ABD = ∠ BAC

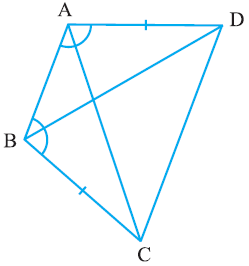
Ans: The given parameters from the questions are ∠DAB = ∠CBA and AD = BC.
(i) ΔABD and ΔBAC are similar by SAS congruency as
AB = BA (It is the common arm)
∠DAB = ∠CBA and AD = BC (These are given in the question)
So, triangles ABD and BAC are similar i.e. ΔABD ≅ ΔBAC. (Hence proved).
(ii) It is now known that ΔABD ≅ ΔBAC so,
BD = AC (by the rule of CPCT).
(iii) Since ΔABD ≅ ΔBAC so,
Angles ∠ABD = ∠BAC (by the rule of CPCT).

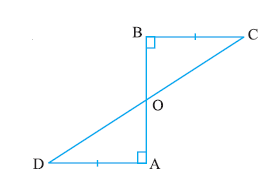
Q3. AD and BC are equal perpendiculars to a line segment AB. Show that CD bisects AB.

Ans: It is given that AD and BC are two equal perpendiculars to AB.
We will have to prove that CD is the bisector of AB
Now,
Triangles ΔAOD and ΔBOC are similar by AAS congruency since:
(i) ∠A = ∠B (They are perpendiculars)
(ii) AD = BC (As given in the question)
(iii) ∠AOD = ∠BOC (They are vertically opposite angles)
∴ ΔAOD ≅ ΔBOC.
So, AO = OB (by the rule of CPCT).
Thus, CD bisects AB (Hence proved).

Q4. l and m are two parallel lines intersected by another pair of parallel lines p and q. Show that ∆ ABC ≅ ∆ CDA.

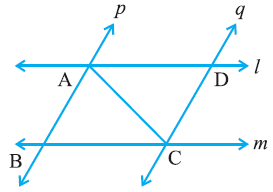
Ans: It is given that p || q and l || m
To prove:
Triangles ABC and CDA are similar i.e. ΔABC ≅ ΔCDA
Proof:
Consider the ΔABC and ΔCDA,
(i) ∠BCA = ∠DAC and ∠BAC = ∠DCA Since they are alternate interior angles
(ii) AC = CA as it is the common arm
So, by ASA congruency criterion, ΔABC ≅ ΔCDA.

Q5. Line l is the bisector of an angle ∠ A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠ A. Show that:
(i) ∆ APB ≅ ∆ AQB
(ii) BP = BQ or B is equidistant from the arms of ∠ A.

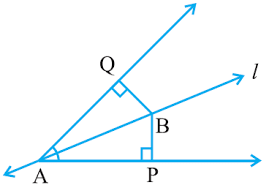
Ans: It is given that the line “l” is the bisector of angle ∠A and the line segments BP and BQ are perpendiculars drawn from l.
(i) ΔAPB and ΔAQB are similar by AAS congruency because:
∠P = ∠Q (They are the two right angles)
AB = AB (It is the common arm)
∠BAP = ∠BAQ (As line l is the bisector of angle A)
So, ΔAPB ≅ ΔAQB.
(ii) By the rule of CPCT, BP = BQ. So, it can be said the point B is equidistant from the arms of ∠A.

Q6. In the following figure, AC = AE, AB = AD and ∠ BAD = ∠ EAC. Show that BC = DE.

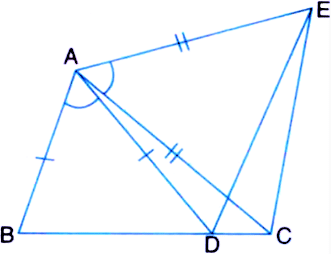
Ans: It is given in the question that AB = AD, AC = AE, and ∠BAD = ∠EAC
To prove:
The line segment BC and DE are similar i.e. BC = DE
Proof:
We know that ∠BAD = ∠EAC
Now, by adding ∠DAC on both sides we get,
∠BAD + ∠DAC = ∠EAC +∠DAC
This implies, ∠BAC = ∠EAD
Now, ΔABC and ΔADE are similar by SAS congruency since:
(i) AC = AE (As given in the question)
(ii) ∠BAC = ∠EAD
(iii) AB = AD (It is also given in the question)
∴ Triangles ABC and ADE are similar i.e. ΔABC ≅ ΔADE.
So, by the rule of CPCT, it can be said that BC = DE.

Q7. AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠ BAD = ∠ ABE and ∠ EPA = ∠ DPB. Show that
(i) ∆ DAP ≅ ∆ EBP
(ii) AD = BE

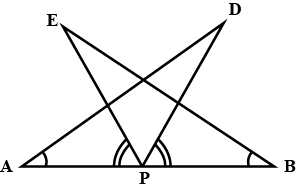
Ans: In the question, it is given that P is the mid-point of line segment AB. Also, ∠BAD = ∠ABE and ∠EPA = ∠DPB
(i) It is given that ∠EPA = ∠DPB
Now, add ∠DPE on both sides,
∠EPA +∠DPE = ∠DPB+∠DPE
This implies that angles DPA and EPB are equal i.e. ∠DPA = ∠EPB
Now, consider the triangles DAP and EBP.
∠DPA = ∠EPB
AP = BP (Since P is the mid-point of the line segment AB)
∠BAD = ∠ABE (As given in the question)
So, by ASA congruency, ΔDAP ≅ ΔEBP.
(ii) By the rule of CPCT, AD = BE.

Q8. In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B. Show that:
(i) ∆ AMC ≅ ∆ BMD
(ii) ∠ DBC is a right angle.
(iii) ∆ DBC ≅ ∆ ACB
(iv) CM = ½ AB

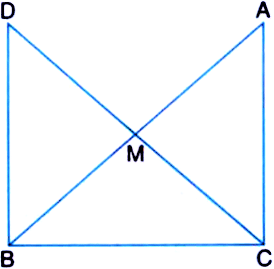
Ans: It is given that M is the mid-point of the line segment AB, ∠C = 90°, and DM = CM
(i) Consider the triangles ΔAMC and ΔBMD:
AM = BM (Since M is the mid-point)
CM = DM (Given in the question)
∠CMA = ∠DMB (They are vertically opposite angles)
So, by SAS congruency criterion, ΔAMC ≅ ΔBMD.
(ii) ∠ACM = ∠BDM (by CPCT)
∴ AC || BD as alternate interior angles are equal.
Now, ∠ACB +∠DBC = 180° (Since they are co-interiors angles)
⇒ 90° +∠B = 180°
∴ ∠DBC = 90°
(iii) In ΔDBC and ΔACB,
BC = CB (Common side)
∠ACB = ∠DBC (They are right angles)
DB = AC (by CPCT)
So, ΔDBC ≅ ΔACB by SAS congruency.
(iv) DC = AB (Since ΔDBC ≅ ΔACB)
⇒ DM = CM = AM = BM (Since M the is mid-point)
So, DM + CM = BM+AM
Hence, CM + CM = AB
⇒ CM = (½) AB

Exercise 7.2

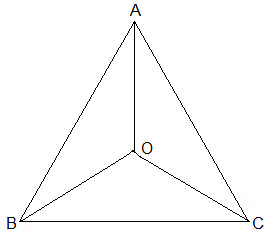
Q1. In an isosceles triangle ABC, with AB = AC, the bisectors of ∠ B and ∠ C intersect each other at O. Join A to O. Show that:
(i) OB = OC
(ii) AO bisects ∠ A

Ans:
Given:
AB = AC and
the bisectors of ∠B and ∠C intersect each other at O
(i) Since ABC is an isosceles with AB = AC,
∠B = ∠C
½ ∠B = ½ ∠C
⇒ ∠OBC = ∠OCB (Angle bisectors)
∴ OB = OC (Side opposite to the equal angles are equal.)
(ii) In ΔAOB and ΔAOC,
AB = AC (Given in the question)
AO = AO (Common arm)
OB = OC (As Proved Already)
So, ΔAOB ≅ ΔAOC by SSS congruence condition.
BAO = CAO (by CPCT)
Thus, AO bisects ∠A.

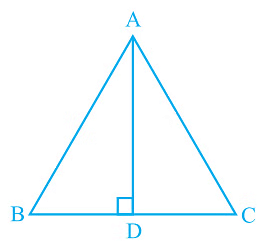
Q2. In ΔABC, AD is the perpendicular bisector of BC (see Fig.). Show that ΔABC is an isosceles triangle in which AB = AC.

Ans: It is given that AD is the perpendicular bisector of BC
To prove:
AB = AC
Proof:
In ΔADB and ΔADC,
AD = AD (It is the Common arm)
∠ADB = ∠ADC
BD = CD (Since AD is the perpendicular bisector)
So, ΔADB ≅ ΔADC by SAS congruency criterion.
Thus,
AB = AC (by CPCT)

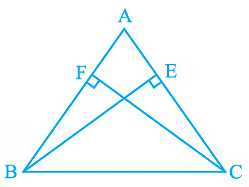
Q3. ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see Fig.). Show that these altitudes are equal.

Ans:
Given:
(i) BE and CF are altitudes.
(ii) AC = AB
To prove:
BE = CF
Proof:
Triangles ΔAEB and ΔAFC are similar by AAS congruency since
∠A = ∠A (It is the common arm)
∠AEB = ∠AFC (They are right angles)
AB = AC (Given in the question)
∴ ΔAEB ≅ ΔAFC and so, BE = CF (by CPCT).

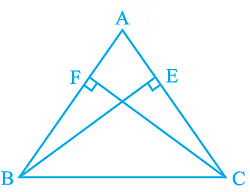
Q4. ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see Fig). Show that
(i) ∆ ABE ≅ ∆ ACF
(ii) AB = AC, i.e., ABC is an isosceles triangle.

Ans: It is given that BE = CF
(i) In ΔABE and ΔACF,
∠A = ∠A (It is the common angle)
∠AEB = ∠AFC (They are right angles)
BE = CF (Given in the question)
∴ ΔABE ≅ ΔACF by AAS congruency condition.
(ii) AB = AC by CPCT and so, ABC is an isosceles triangle.

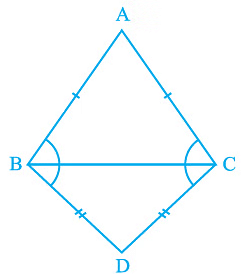
Q5. ABC and DBC are two isosceles triangles on the same base BC (see Fig). Show that ∠ ABD = ∠ ACD.

Ans: In the question, it is given that ABC and DBC are two isosceles triangles.
We will have to show that ∠ABD = ∠ACD
Proof:
Triangles ΔABD and ΔACD are similar by SSS congruency since
AD = AD (It is the common arm)
AB = AC (Since ABC is an isosceles triangle)
BD = CD (Since BCD is an isosceles triangle)
So, ΔABD ≅ ΔACD.
∴ ∠ABD = ∠ACD by CPCT.

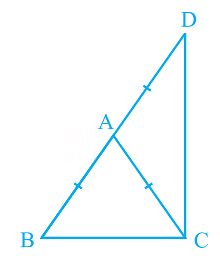
Q6. ∆ABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see Fig). Show that ∠ BCD is a right angle.

Ans: It is given that AB = AC and AD = AB
We will have to now prove ∠BCD is a right angle.
Proof:
Consider ΔABC,
AB = AC (It is given in the question)
Also, ∠ACB = ∠ABC (They are angles opposite to the equal sides and so, they are equal)
Now, consider ΔACD,
AD = AB
Also, ∠ADC = ∠ACD (They are angles opposite to the equal sides and so, they are equal)
Now,
In ΔABC,
∠CAB + ∠ACB + ∠ABC = 180°
So, ∠CAB + 2∠ACB = 180°
⇒ ∠CAB = 180° – 2∠ACB — (i)
Similarly, in ΔADC,
∠CAD = 180° – 2∠ACD — (ii)
also,
∠CAB + ∠CAD = 180° (BD is a straight line.)
Adding (i) and (ii) we get,
∠CAB + ∠CAD = 180° – 2∠ACB+180° – 2∠ACD
⇒ 180° = 360° – 2∠ACB-2∠ACD
⇒ 2(∠ACB+∠ACD) = 180°
⇒ ∠BCD = 90°

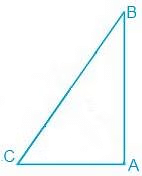
Q7. ABC is a right angled triangle in which ∠ A = 90° and AB = AC. Find ∠ B and ∠ C.
Ans:

In the question, it is given that

∠A = 90° and AB = AC
AB = AC
⇒ ∠B = ∠C (They are angles opposite to the equal sides and so, they are equal)
Now,
∠A+∠B+∠C = 180° (Since the sum of the interior angles of the triangle)
∴ 90° + 2∠B = 180°
⇒ 2∠B = 90°
⇒ ∠B = 45°
So, ∠B = ∠C = 45°

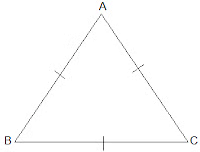
Q8. Show that the angles of an equilateral triangle are 60° each.
Ans: Let ABC be an equilateral triangle as shown below:
Here, BC = AC = AB (Since the length of all sides is same)⇒ ∠A = ∠B =∠C (Sides opposite to the equal angles are equal.)Also, we know that
∠A+∠B+∠C = 180°
⇒ 3∠A = 180°
⇒ ∠A = 60°
∴ ∠A = ∠B = ∠C = 60°
So, the angles of an equilateral triangle are always 60° eac

Exercise 7.3

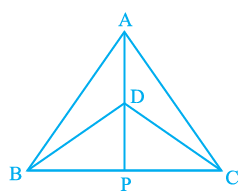
Q1. ∆ ABC and ∆ DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Fig). If AD is extended to intersect BC at P, show that
(i) ΔABD ≅ ΔACD 
(ii) ΔABP ≅ ΔACP 
(iii) AP bisects ∠A as well as ∠D. 
(iv) AP is the perpendicular bisector of BC.

Ans: In the above question, it is given that ΔABC and ΔDBC are two isosceles triangles.
(i) ΔABD and ΔACD are similar by SSS congruency because:
AD = AD (It is the common arm)
AB = AC (Since ΔABC is isosceles)
BD = CD (Since ΔDBC is isosceles)
∴ ΔABD ≅ ΔACD.
(ii) ΔABP and ΔACP are similar as:
AP = AP (It is the common side)
∠PAB = ∠PAC (by CPCT since ΔABD ≅ ΔACD)
AB = AC (Since ΔABC is isosceles)
So, ΔABP ≅ ΔACP by SAS congruency condition.
(iii) ∠PAB = ∠PAC by CPCT as ΔABD ≅ ΔACD.
AP bisects ∠A. — (i)
Also, ΔBPD and ΔCPD are similar by SSS congruency as
PD = PD (It is the common side)
BD = CD (Since ΔDBC is isosceles.)
BP = CP (by CPCT as ΔABP ≅ ΔACP)
So, ΔBPD ≅ ΔCPD.
Thus, ∠BDP = ∠CDP by CPCT. — (ii)
Now by comparing (i) and (ii) it can be said that AP bisects ∠A as well as ∠D.
(iv) ∠BPD = ∠CPD (by CPCT as ΔBPD ΔCPD)
and BP = CP — (i)
also,
∠BPD +∠CPD = 180° (Since BC is a straight line.)
⇒ 2∠BPD = 180°
⇒ ∠BPD = 90° —(ii)
Now, from equations (i) and (ii), it can be said that
AP is the perpendicular bisector of BC.

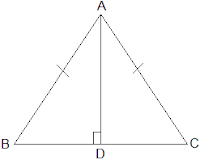
Q2. AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that
(i) AD bisects BC 
(ii) AD bisects ∠ A.
Ans: It is given that AD is an altitude and AB = AC. The diagram is as follows:

(i) In ΔABD and ΔACD,

∠ADB = ∠ADC = 90°
AB = AC (It is given in the question)
AD = AD (Common arm)
∴ ΔABD ≅ ΔACD by RHS congruence condition.
Now, by the rule of CPCT,
BD = CD.
So, AD bisects BC
(ii) Again, by the rule of CPCT, ∠BAD = ∠CAD
Hence, AD bisects ∠A.

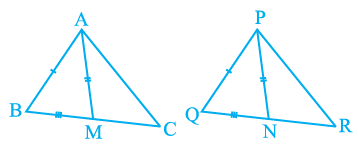
Q3. Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of ΔPQR (see Fig). Show that:
(i) ΔABM ≅ ΔPQN 
(ii) ΔABC ≅ ΔPQR

Ans: Given parameters are:
AB = PQ,
BC = QR and
AM = PN
(i) ½ BC = BM and ½ QR = QN (Since AM and PN are medians)
Also, BC = QR
So, ½ BC = ½ QR
⇒ BM = QN
In ΔABM and ΔPQN,
AM = PN and AB = PQ (As given in the question)
BM = QN (Already proved)
∴ ΔABM ≅ ΔPQN by SSS congruency.
(ii) In ΔABC and ΔPQR,
AB = PQ and BC = QR (As given in the question)
∠ABC = ∠PQR (by CPCT)
So, ΔABC ≅ ΔPQR by SAS congruency.

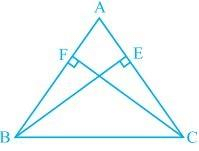
Q4. BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.

Ans: It is known that BE and CF are two equal altitudes.
Now, in ΔBEC and ΔCFB,
∠BEC = ∠CFB = 90° (Same Altitudes)
BC = CB (Common side)
BE = CF (Common side)
So, ΔBEC ≅ ΔCFB by RHS congruence criterion.
Also, ∠C = ∠B (by CPCT)
Therefore, AB = AC as sides opposite to the equal angles is always equal.

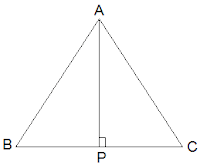
Q5. ABC is an isosceles triangle with AB = AC. Draw AP ⊥ BC to show that ∠ B = ∠ C.
Ans:

In the question, it is given that AB = AC

Now, ΔABP and ΔACP are similar by RHS congruency as
∠APB = ∠APC = 90° (AP is altitude)
AB = AC (Given in the question)
AP = AP (Common side)
So, ΔABP ≅ ΔACP.
∴ ∠B = ∠C (by CPCT)

Exercise 6.1

Q1. In Fig. 6.13, lines AB and CD intersect at O. If ∠AOC +∠BOE = 70° and ∠BOD = 40°, find ∠BOE and reflex ∠COE.
Ans: From the diagram, we have

Since AB is a straight line,
∴ ∠AOC + ∠COE + ∠EOB = 180°
or (∠AOC + ∠BOE) + ∠COE = 180° or 70° + ∠COE = 180° [ ∵∠AOC + ∠BOE = 70° (Given)]
or ∠COE = 180° – 70° = 110°
∴ Reflex ∠COE = 360° – 110° = 250°
Also, AB and CD intersect at O.
∴∠COA = ∠BOD [Vertically opposite angles]
But ∠BOD = 40° [Given]
∴ ∠COA = 40°
Also, ∠AOC + ∠BOE = 70°
∴ 40° + ∠BOE = 70° or ∠BOE = 70° -40° = 30°
Thus, ∠BOE = 30° and reflex ∠COE = 250°.

Q2. In the following figure, lines XY and MN intersect at O. If ∠POY = 90° and a : b = 2 : 3, find c.

Ans:We know that the sum of linear pair are always equal to 180°
So,
POY +a +b = 180°
Putting the value of POY = 90° (as given in the question) we get,
a+b = 90°
Now, it is given that a : b = 2 : 3 so,
Let a be 2x and b be 3x
∴ 2x+3x = 90°
Solving this we get
5x = 90°
So, x = 18°
∴ a = 2×18° = 36°
Similarly, b can be calculated and the value will be
b = 3×18° = 54°
From the diagram, b+c also forms a straight angle so,
b+c = 180°
c+54° = 180°
∴ c = 126°

Q3. In the following figure, ∠PQR = ∠PRQ, then prove that ∠PQS = ∠PRT.

Ans: Since ST is a straight line so,
∠PQS+∠PQR = 180° (linear pair) and
∠PRT+∠PRQ = 180° (linear pair)
Now, ∠PQS + ∠PQR = ∠PRT+∠PRQ = 180°
Since ∠PQR =∠PRQ (as given in the question)
∠PQS = ∠PRT. (Hence proved).

Q4. In the following figure, if x + y = w + z, then prove that AOB is a line.

Ans: For proving AOB is a straight line, we will have to prove x+y is a linear pair
i.e. x+y = 180°
We know that the angles around a point are 360° so,
x + y + w + z = 360°
In the question, it is given that,
x+y = w+z
So, (x+y)+(x+y) = 360°
2(x+y) = 360°
∴ (x+y) = 180° (Hence proved).

Q5. In the adjoining figure, POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that ∠ROS = ½ (∠QOS – ∠POS).

Ans: In the question, it is given that (OR ⊥ PQ) and POQ = 180°
So, POS+ROS+ROQ = 180°
Now, POS+ROS = 180°- 90° (Since POR = ROQ = 90°)
∴ POS + ROS = 90°
Now, QOS = ROQ+ROS
It is given that ROQ = 90°,
∴ QOS = 90° +ROS
Or, QOS – ROS = 90°
As POS + ROS = 90° and QOS – ROS = 90°, we get
POS + ROS = QOS – ROS
2 ROS + POS = QOS
Or, ROS = ½ (QOS – POS) (Hence proved).

Q6. It is given that ∠XYZ = 64° and XY is produced to point P. Draw a figure from the given information. If ray YQ bisects ∠ZYP, find ∠XYQ and reflex ∠QYP.
Ans:

Here, XP is a straight lineSo, XYZ +ZYP = 180°
Putting the value of XYZ = 64° we get,
64° +ZYP = 180°
∴ ZYP = 116°
From the diagram, we also know that ZYP = ZYQ + QYP
Now, as YQ bisects ZYP,
ZYQ = QYP
Or, ZYP = 2ZYQ
∴ ZYQ = QYP = 58°
Again, XYQ = XYZ + ZYQ
By putting the value of XYZ = 64° and ZYQ = 58° we get.
XYQ = 64°+58°
Or, XYQ = 122°
Now, reflex QYP = 180°+XYQ
We computed that the value of XYQ = 122°.
So,
QYP = 180°+122°
∴ QYP = 302°

Exercise 6.2

Q1. In the following Figure, if AB CD, CD EF and y : z = 3 : 7, find x.

Ans: AB || CD, and CD || EF [Given]
∴ AB || EF
∴ x = z [Alternate interior angles] ….(1)
Again, AB || CD
⇒ x + y = 180° [Co-interior angles]
⇒ z + y = 180° … (2) [By (1)]
But y : z = 3 : 7
⇒ 10z = 7 x 180°
⇒ z = 7 x 180° /10 = 126°
From (1) and (3), we have
x = 126°.

Q2. In the following figure, if AB || CD, EF ⊥ CD and ∠GED = 126°, find ∠AGE, ∠GEF and ∠FGE.
Ans: Since AB || CD, GE is a transversal.
It is given that ∠GED = 126°
So, ∠GED = ∠AGE = 126° (As they are alternate interior angles)
Also,
∠GED = ∠GEF +∠FED
As EF⊥ CD, ∠FED = 90°
∴ ∠GED = ∠GEF+90°
Or, ∠GEF = 126° – 90° = 36°
Again, ∠FGE +∠GED = 180° (Transversal)
Putting the value of ∠GED = 126°, we get
∠FGE = 54°
So,
∠AGE = 126°
∠GEF = 36° and
∠FGE = 54°

Q3. In the following figure, if PQ || ST, ∠PQR = 110° and ∠RST = 130°, find ∠QRS.
[Hint : Draw a line parallel to ST through point R.]

Ans: First, construct a line XY parallel to PQ.

We know that the angles on the same side of transversal is equal to 180°.
So, ∠PQR+∠QRX = 180°
Or, ∠QRX = 180°-110°
∴ ∠QRX = 70°
Similarly,
∠RST +∠SRY = 180°
Or, ∠SRY = 180°- 130°
∴ ∠SRY = 50°
Now, for the linear pairs on the line XY-
∠QRX+∠QRS+∠SRY = 180°
Putting their respective values, we get
∠QRS = 180° – 70° – 50°
Hence, ∠QRS = 60°

Q4. In the following figure, if AB || CD, ∠ APQ = 50° and ∠ PRD = 127°, find x and y
Ans: From the diagram,
∠APQ = ∠PQR (Alternate interior angles)
Now, putting the value of ∠APQ = 50° and ∠PQR = x, we get
x = 50°
Also,
∠APR = ∠PRD (Alternate interior angles)
Or, ∠APR = 127° (As it is given that ∠PRD = 127°)
We know that
∠APR = ∠APQ+∠QPR
Now, putting values of ∠QPR = y and ∠APR = 127°, we get
127° = 50°+ y
Or, y = 77°
Thus, the values of x and y are calculated as:
x = 50° and y = 77°

Q5. In the following figure, PQ and RS are two mirrors placed parallel to each other. An incident ray AB strikes the mirror PQ at B, the reflected ray moves along the path BC and strikes the mirror RS at C and again reflects back along CD. Prove that AB || CD.

Ans: First, draw two lines, BE and CF, such that BE ⊥ PQ and CF ⊥ RS.
Now, since PQ || RS,
So, BE || CF

We know that,
Angle of incidence = Angle of reflection (By the law of reflection)
So,
∠1 = ∠2 and
∠3 = ∠4
We also know that alternate interior angles are equal. Here, BE ⊥ CF and the transversal line BC cuts them at B and C
So, ∠2 = ∠3 (As they are alternate interior angles)
Now, ∠1 +∠2 = ∠3 +∠4
Or, ∠ABC = ∠DCB
So, AB || CD (alternate interior angles are equal)

Q1: Which of the following statements are true and which are false? Give reasons for your answers.
(i) Only one line can pass through a single point.
(ii) There are an infinite number of lines which pass through two distinct points.
(iii) A terminated line can be produced indefinitely on both the sides
(iv) If two circles are equal, then their radii are equal.
(v) In Fig. 5.9, if AB = PQ and PQ = XY, then AB = XY.

Ans: (i) False

Reason: There can be infinite number of lines that can be drawn through a single point. Hence, the statement mentioned is False

(ii) False

Reason: Through two distinct points, there can be only one line that can be drawn. Hence, the statement mentioned is False

(iii) True

Reason: A line that is terminated can be indefinitely produced on both sides as a line can be extended on both its sides infinitely. Hence, the statement mentioned is True.

(iv) True

Reason: The radii of two circles are equal when the two circles are equal. The circumference and the centre of both the circles coincide; and thus, the radius of the two circles should be equal. Hence, the statement mentioned is True.

(v) True

Reason: According to Euclid’s 1^st axiom- “Things which are equal to the same thing are also equal to one another”. Hence, the statement mentioned is True.

Q2: Give a definition for each of the following terms. Are there other terms that need to be defined first? What are they, and how might you define them?
(i) parallel lines 
(ii) perpendicular lines 
(iii) line segment 
(iv) radius of a circle 
(v) square
Ans: Yes, we need to have an idea about the terms, point, line, ray, angle, plane, circle and quadrilateral, etc. before defining the required terms.
Point: A small dot made by a sharp pencil on the surface of paper gives an idea about a point.
It has no dimensions. It has only a position.
Line: A line is an idea that it should be straight and that it should extend indefinitely in both directions. It has no endpoints and has no definite length.

Note: In geometry, a line means “The line in its totality and not a portion of it. Whereas a physical example of a perfect line is not possible. A line extends indefinitely in both directions, so we cannot draw or show it wholly on paper. That is why we mark arrowheads on both ends, indicating that it extends indefinitely in both directions.

Ray: A part of a line that has only one endpoint and extends indefinitely in one direction. A ray has no definite length.
Angle: Two rays having a common endpoint form an angle.
Plane: A plane is a surface such that every point of the line joining any two points on it, lies on it.
Circle: A circle is the set of all those points in a given plane that are equidistant from a fixed point in the same plane. The fixed point is called the centre of the circle.
Quadrilateral: A closed figure made of four line segments is called a quadrilateral.
Definitions of the required terms are given below: 
(i) Parallel Lines: Two lines ‘n’ and ‘m’ in a plane are said to be parallel if they have no common point and we write them as n || m.

Note: The distance between two parallel lines always remains the same.

(ii) Perpendicular Lines: Two lines ‘p’ and ‘q’ lying in the same plane are said to be perpendicular if they form a right angle and we write them as p ⊥ q.

(iii) Line Segment: A line segment is a part of the line having a definite length. It has two end-points.
In the figure, a line segment is shown having endpoints ‘A’ and ‘B’. It is written as  or 

(iv) Radius of a circle: The distance from the centre to a point on the circle is called the radius of the circle. In the figure, P is the centre and Q is a point on the circle, then PQ is the radius.

(v) Square: A quadrilateral in which all the four angles are right angles and all the four sides are equal is called a square. In the figure, PQRS is a square.

Q3. Consider two ‘postulates’ given below:
(i) Given any two distinct points A and B, there exists a third point C which is in between A and B.
(ii) There exist at least three points that are not on the same line.
Do these postulates contain any undefined terms? Are these postulates consistent?
Do they follow Euclid’s postulates? Explain.
Ans: Yes, these postulates contain undefined terms. Undefined terms in the postulates are

• There are many points that lie in a plane. But, in the postulates given here, the position of point C is not given as to whether it lies on the line segment joining AB or not.
• On top of that, there is no information about whether the points are in the same plane or not.

And
Yes, these postulates are consistent when we deal with these two situations:

• Point C is lying on the line segment AB in between A and B.
• Point C does not lie on line segment AB.

No, they don’t follow Euclid’s postulates. They follow the axioms.

Q4. If a point C lies between two points A and B such that AC = BC, then prove that AC =  (1/2)AB. Explain by drawing the figure.
Ans: 

Given that, AC = BC
Now, adding AC on both sides,
L.H.S.+AC = R.H.S.+AC
AC+AC = BC+AC
2AC = BC+AC
We know that BC+AC = AB (as it coincides with line segment AB)
∴ 2 AC = AB (If equals are added to equals, the wholes are equal.)
⇒ AC = (½)AB

Q5. In Question 4, point C is called a mid-point of line segment AB. Prove that every line segment has one and only one mid-point.
Ans: Let AB be the line segment.
Assume that points P and Q are the two different midpoints of AB.
Now,
∴ P and Q are the midpoints of AB.
Therefore,
AP = PB and AQ = QB
also,
PB+AP = AB (as it coincides with line segment AB)
Similarly, QB+AQ = AB
Now,
Adding AP to the L.H.S. and R.H.S. of the equation AP = PB
We get AP+AP = PB+AP (If equals are added to equals, the wholes are equal.)
⇒ 2AP = AB — (i)
Similarly,
2 AQ = AB — (ii)
From (i) and (ii), Since R.H.S. are the same, we equate the L.H.S.
2 AP = 2 AQ (Things which are equal to the same thing are equal to one another.)
⇒ AP = AQ (Things which are double of the same things are equal to one another.)
Thus, we conclude that P and Q are the same points.
This contradicts our assumption that P and Q are two different midpoints of AB.
Thus, it is proved that every line segment has one and only one midpoint.
Hence, proved.

Q6. In the figure, given below, if AC = BD, then prove that AB = CD.
Ans:

It is given AC = BD
From the given figure, we get
AC = AB+BC
BD = BC+CD
⇒ AB+BC = BC+CD [AC = BD, given]
We know that, according to Euclid’s axiom, when equals are subtracted from equals, remainders are also equal.
Subtracting BC from the L.H.S. and R.H.S. of the equation AB+BC = BC+CD, we get
AB+BC-BC = BC+CD-BC
AB = CD
Hence, proved.

Q7. Why is Axiom 5, in the list of Euclid’s axioms, considered a ‘universal truth’? (Note that the question is not about the fifth postulate.)
Ans: Axiom 5: The whole is always greater than the part.
For Example: A cake. When it is whole or complete, assume that it measures 2 pounds but when a part from it is taken out and measured, its weight will be smaller than the previous measurement. So, the fifth axiom of Euclid is true for all the materials in the universe. Hence, Axiom 5, in the list of Euclid’s axioms, is considered a ‘universal truth’.

Exercise 4.1

Q1. The cost of a notebook is twice the cost of a pen. Write a linear equation in two variables to represent this statement. (Take the cost of a notebook to be ₹ x and that of a pen to be ₹ y)
Ans: Let the cost of a notebook be = ₹ x
Let the cost of a pen be = ₹ y
According to the question,
The cost of a notebook is twice the cost of a pen.
i.e., cost of a notebook = 2×cost of a pen
x = 2 × y
x = 2y
x – 2y = 0
x – 2y = 0 is the linear equation in two variables to represent the statement, ‘The cost of a notebook is twice the cost of a pen.’

Q2. Express the following linear equations in the form ax + by + c = 0 and indicate the values of a, b and c in each case:
(i) 2x + 3y= 
Ans: Consider 2x + 3y=     Equation (1)
⇒ 2x + 3y – = 0
Comparing this equation with the standard form of the linear equation in two variables, ax + by + c = 0 we have,
a = 2
b = 3
c = – 

(ii) x – (y/5) – 10 = 0
Ans: The equation x –(y/5)-10 = 0 can be written as,
(1)x+(-1/5)y +(–10) = 0
Now comparing x+(-1/5)y+(–10) = 0 with ax+by+c = 0
We get,
a = 1
b = -(1/5)
c = -10

(iii) –2x + 3y = 6
Ans: –2x+3y = 6
Re-arranging the equation, we get,
–2x+3y–6 = 0
The equation –2x+3y–6 = 0 can be written as,
(–2)x+(3)y+(– 6) = 0
Now, comparing (–2)x+(3)y+(–6) = 0 with ax+by+c = 0
We get, a = –2
b = 3
c =-6

(iv) x = 3y
Ans: x = 3y
Re-arranging the equation, we get,
x-3y = 0
The equation x-3y=0 can be written as,
(1)x+(-3)y+(0)c = 0
Now comparing 1x+(-3)y+(0)c = 0 with ax+by+c = 0
We get a = 1
b = -3
c = 0

(v) 2x = –5y
Ans: 2x = –5y
Re-arranging the equation, we get,
2x+5y = 0
The equation 2x+5y = 0 can be written as,
2x+5y+0 = 0
Now, comparing (2)x+(5)y+0= 0 with ax+by+c = 0
We get a = 2
b = 5
c = 0

(vi) 3x + 2 = 0
Ans: 3x+2 = 0
The equation 3x+2 = 0 can be written as,
3x+0y+2 = 0
Now comparing 3x+0+2= 0 with ax+by+c = 0
We get a = 3
b = 0
c = 2

(vii) y–2 = 0
Ans: y–2 = 0
The equation y–2 = 0 can be written as,
(0)x+(1)y+(–2) = 0
Now comparing (0)x+(1)y+(–2) = 0with ax+by+c = 0
We get a = 0
b = 1
c = –2

(viii) 5 = 2x
Ans: 5 = 2x
Re-arranging the equation, we get,
2x = 5
i.e., 2x–5 = 0
The equation 2x–5 = 0 can be written as,
2x+0y–5 = 0
Now comparing 2x+0y–5 = 0 with ax+by+c = 0
We get a = 2
b = 0
c = -5

Exercise 4.2

Q1. Which one of the following options is true, and why?
y = 3x + 5 has

(i) A unique solution

(ii) Only two solutions

(iii) Infinitely many solutions

Ans: Let us substitute different values for x in the linear equation y = 3x + 5,

From the table, it is clear that x can have infinite values, and for all the infinite values of x, there are infinite values of y as well.
Hence, (iii) infinitely many solutions is the only option true.

Q2. Write four solutions for each of the following equations:
(i) 2x + y = 7
Ans: To find the four solutions of 2x + y =7 we substitute different values for x and y

Let x = 0
Then,
2x + y = 7
(2)(0) + y = 7
y = 7

(0, 7)
Let x = 1
Then,
2x + y = 7
(2 × 1) + y = 7
2 + y = 7
y = 7 – 2
y = 5
(1, 5)
Let y = 1
Then,
2x + y = 7
(2x) + 1 = 7
2x = 7 – 1
2x = 6
x = 6/2
x = 3
(3, 1)
Let x = 2
Then,
2x + y = 7
(2 × 2) + y = 7
4 + y = 7
y =7 – 4
y = 3
(2, 3)
The solutions are (0, 7), (1, 5), (3, 1), (2, 3)

(ii) πx + y = 9
Ans: To find the four solutions of πx+y = 9 we substitute different values for x and y
Let x = 0
Then,
πx + y = 9
(π)(0) + y = 9
y = 9
(0, 9)
Let x = 1
Then,
πx + y = 9
(π × 1) + y = 9
π + y = 9
y = 9-π
(1, 9-π)
Let y = 0
Then,
πx + y = 9
πx + 0 = 9
πx = 9
x = 9/π
(9/π,0)
Let x = -1
Then,
πx + y = 9
π(-1)+y = 9

-π+y=9
y = 9 + π
(-1, 9+π)
The solutions are (0, 9), (1, 9-π), (9/π, 0), (-1, 9+π)
(iii) x = 4y
Ans: To find the four solutions of x = 4y we substitute different values for x and y
Let x = 0
Then,
x = 4y
0 = 4y
4y = 0
y = 0/4
y = 0
(0, 0)
Let x = 1
Then,
x = 4y
1 = 4y
4y = 1
y = 1/4
(1, 1/4)
Let y = 4
Then,
x = 4y
x= 4 × 4
x = 16
(16, 4)
Let y =
Then,
x = 4y
x = 4×1
x = 4
(4,1)
The solutions are (0,0), (1,1/4), (16,4), (4,1)

Q3. Check which of the following are solutions of the equation x–2y = 4 and which are not:
(i) (0, 2)
Ans: (x, y) = (0, 2)
Here, x = 0 and y = 2
Substituting the values of x and y in the equation x – 2y = 4, we get,
x – 2y = 4
⟹ 0 – (2 × 2) = 4
But, -4 ≠4
Therefore, (0, 2) is not a solution of the equation x – 2y = 4

(ii) (2, 0)
Ans: (x,y) = (2, 0)
Here, x = 2 and y = 0
Substituting the values of x and y in the equation x – 2y = 4, we get,
x – 2y = 4
⟹ 2-(2 × 0) = 4
⟹ 2 – 0 = 4
But, 2 ≠ 4
(2, 0) is not a solution of the equation x – 2y = 4

(iii) (4, 0)
Ans: (x, y) = (4, 0)
Here, x = 4 and y = 0
Substituting the values of x and y in the equation x – 2y = 4, we get,
x – 2y = 4
⟹ 4 – 2 × 0 = 4
⟹ 4-0 = 4
⟹ 4 = 4
(4, 0) is a solution of the equation x – 2y = 4

(iv) (√2, 4√2)
Ans: (x, y) = (√2, 4√2)
Here, x = √2 and y = 4√2
Substituting the values of x and y in the equation x – 2y = 4, we get,
x –2y = 4
⟹ √2-(2×4√2) = 4
√2-8√2 = 4
But, -7√2 ≠ 4
(√2, 4√2) is not a solution of the equation x – 2y = 4

(v) (1, 1)
Ans: (x, y) = (1, 1)
Here, x = 1 and y = 1
Substituting the values of x and y in the equation x – 2y = 4, we get,
x – 2y = 4
⟹ 1 -(2 × 1) = 4
⟹ 1 – 2 = 4
But, -1 ≠ 4
(1, 1) is not a solution of the equation x–2y = 4

Q4. Find the value of k, if x = 2, y = 1 is a solution of the equation 2x+3y = k.
Ans: The given equation is
2x + 3y = k
According to the question, x = 2 and y = 1.
Now, Substituting the values of x and y in the equation 2x + 3y = k,
We get,
(2 × 2)+(3 × 1) = k
⟹ 4 + 3 = k
⟹ 7 = k
k = 7
The value of k, if x = 2, y = 1 is a solution of the equation 2x + 3y = k, is 7.

Exercise 3.1

Q1. How will you describe the position of a table lamp on your study table to another person?
Ans:

The above figure is a 3-D shows a study table, on which a study lamp is placed.
Now let us consider only the top surface of the table which becomes a 2-D rectangle figure.

From the Figure Above,

• Consider the lamp on the table as a point
• Consider the table as a 2-D plane.

The table has a shorter side (20 cm) and a longer side (30 cm).

• Let us measure the distance of the lamp from the shorter side and the longer side.
• Let us assume
  • Distance of the lamp from the shorter side is 5 cm.
  • Distance of the lamp from the longer side is 5 cm.

Therefore, we can conclude that the position of the lamp on the table can be described with respect to the order of the axes as (5,15).

Q2. (Street Plan): A city has two main roads which cross each other at the center of the city.
These two roads are along the North–South direction and East– West direction.
All the other streets of the city run parallel to these roads and are 200 m apart. There are 5 streets in each direction. Using 1cm = 200 m, draw a model of the city on your notebook. Represent the roads/streets by single lines. There are many cross- streets in your model. A particular cross-street is made by two streets, one running in the North–South direction and another in the East– West direction. Each cross street is referred to in the following manner:
If the 2nd street running in the North–South direction and 5th in the East–West direction meet at some crossing, then we will call this cross-street (2, 5).
Using this convention, find:
(i) How many cross – streets can be referred to as (4, 3).
(ii) How many cross – streets can be referred to as (3, 4).
Ans: Let us draw two perpendicular lines as the two main roads of the city that cross each other at the center. Let us mark them as North–South and East–West.
As given in the question, let us take the scale as 1cm = 200 m.
Draw five streets that are parallel to both the main roads (which intersect), to get the given below figure.
Street plan is as shown in the figure:

(i) There is only one cross street, which can be referred as (4, 3).
(ii) There is only one cross street, which can be referred as (3, 4).
Exercise 3.2

Q1. Write the answer of each of the following questions:
(i) What is the name of horizontal and the vertical lines drawn to determine the position of any point in the Cartesian plane?
(ii) What is the name of each part of the plane formed by these two lines?
(iii) Write the name of the point where these two lines intersect.
Ans: (i) The horizontal line that is drawn to determine the position of any point in the Cartesian plane is called as x-axis. The vertical line that is drawn to determine the position of any point in the Cartesian plane is called as y-axis.

(ii) The name of each part of the plane that is formed by x-axis and y-axis is called as quadrant.

(iii) The point, where the x-axis and the y-axis intersect is called as origin (O).

Q2. See the given figure, and write the following:
(i) The coordinates of B.
(ii) The coordinates of C.
(iii) The point identified by the coordinates (–3, –5).
(iv) The point identified by the coordinates (2, –4).
(v) The abscissa of the point D.
(vi) The ordinate of the point H.
(vii) The coordinates of the point L.
(viii) The coordinates of the point M.
Ans:

From the Figure above,
(i) The co-ordinates of point B is the distance of point B from x-axis and y-axis.
Therefore, the co-ordinates of point B are (–5, 2).
(ii) The co-ordinates of point C is the distance of point C from x-axis and y-axis.
Therefore, the co-ordinates of point C are (5, –5).
(iii) The point that represents the co-ordinates (–3, –5) is E.
(iv) The point that represents the co-ordinates (2, –4) is G.
(v) The abscissa of point D is the distance of point D from the y-axis. Therefore, the abscissa of point D is 6.
(vi) The ordinate of point H is the distance of point H from the x-axis. Therefore, the abscissa of point H is –3.
(vii) The co-ordinates of point L in the above figure is the distance of point L from x-axis and y-axis. Therefore, the co-ordinates of point L are (0, 5).
(viii) The co-ordinates of point M in the above figure is the distance of point M from x-axis and y-axis. Therefore, the co-ordinates of point M are (–3, 0).

Q1: Use suitable identities to find the following products: 
(i) (x + 4)(x + 10)

Ans: Using the identity (x + a)(x + b) = x² + (a + b)x + ab,
[Here, a = 4 and b = 10]
We get,
(x + 4)(x + 10) = x² + (4 + 10)x + (4 x 10)
= x² + 14x + 40

(ii) (x + 8)(x – 10)

Ans: Using the identity, (x+a)(x+b) = x²+(a+b)x+ab
[Here, a = 8 and b = (–10)]
We get: (x + 8)(x – 10) = x² + [8 + (–10)]x + [8 x (–10)]
= x² + [8-10]x + [–80]
= x² – 2x – 80

(iii) (3x + 4)(3x – 5)

Ans: Using the identity (x + a)(x + b) = x² + (a + b)x + ab,
[Here, x = 3x, a = 4 and b = −5]
we get
(3x + 4)(3x – 5) = (3x)² + [4 + (–5)]3x + [4 x (–5)]
= 9x² + 3x(4–5)–20
= 9x² – 3x – 20

(iv) (y² + 3/2) (y² – 3/2)

Ans: Using the identity (x + y)(x – y) = x² – y²,
[Here, x = y² and y = 3/2]
we get:
(y²+3/2)(y²–3/2) = (y²)²–(3/2)²
= y⁴–9/4

(v) (3 – 2x) (3 + 2x)

Ans: Using (a + b) (a – b) = a² – b²,
putting a = 3 , b = 2x
= (3)² – (2x)²
= 9 – 4x²

Q2: Evaluate the following products without multiplying directly: 
(i) 103 × 107

Ans: (100+3) × (100+7)
Using identity, [(x+a)(x+b) = x²+(a+b)x+ab
Here, x = 100
a = 3
b = 7
We get, 103×107 = (100+3)×(100+7)
= (100)²+(3+7)100+(3×7))
= 10000+1000+21
= 11021

(ii) 95×96

Ans: (100-5)×(100-4)
Using identity, [(x-a)(x-b) = x²-(a+b)x+ab
Here, x = 100
a = -5
b = -4
We get, 95×96 = (100-5)×(100-4)
= (100)²+100(-5+(-4))+(-5×-4)
= 10000-900+20
= 9120

(iii) 104 × 96

Ans: (100+4)×(100–4)
Using identity, [(a+b)(a-b)= a2-b2]
Here, a = 100
b = 4
We get, 104×96 = (100+4)×(100–4)
= (100)²–(4)2
= 10000–16
= 9984

Q3: Factorise the following using appropriate identities: 
(i) 9x² + 6xy + y² 

Ans: (3x)²+(2×3x×y)+y²
Using identity, x²+2xy+y² = (x+y)²
Here, x = 3x
y = y
9x²+6xy+y² = (3x)²+(2×3x×y)+y²
= (3x+y)²
= (3x+y)(3x+y)

(ii) 4y² – 4y + 1

Ans: 4y²−4y+1 = (2y)²–(2×2y×1)+1
Using identity, x² – 2xy + y² = (x – y)²
Here, x = 2y
y = 1
4y²−4y+1 = (2y)²–(2×2y×1)+12
= (2y–1)²
= (2y–1)(2y–1)

(iii) x²– y²/100

Ans: x²–y²/100 = x²–(y/10)²
Using identity, x²-y² = (x-y)(x+y)
Here, x = x
y = y/10
x²–y²/100 = x²–(y/10)²
= (x–y/10)(x+y/10)

 Q4: Expand each of the following, using suitable identities:
(i) (x + 2y + 4z)²

Ans: Using identity, (x+y+z)² = x²+y²+z²+2xy+2yz+2zx
Here, x = x
y = 2y
z = 4z
(x+2y+4z)² = x²2+(2y)²+(4z)²+(2×x×2y)+(2×2y×4z)+(2×4z×x)
= x²+4y²+16z²+4xy+16yz+8xz

(ii) (2x – y + z)²

Ans: Using identity, (x+y+z)² = x²+y²+z²+2xy+2yz+2zx
Here, x = 2x
y = −y
z = z
(2x−y+z)² = (2x)²+(−y)²+z²+(2×2x×−y)+(2×−y×z)+(2×z×2x)
= 4x²+y²+z²–4xy–2yz+4xz

(iii) (–2x + 3y + 2z)²

Ans: Using identity, (x+y+z)² = x²+y²+z²+2xy+2yz+2zx
Here, x = −2x
y = 3y
z = 2z
(−2x+3y+2z)² = (−2x)2+(3y)²+(2z)²+(2×−2x×3y)+(2×3y×2z)+(2×2z×−2x)
= 4x²+9y²+4z²–12xy+12yz–8xz

(iv) (3a – 7b – c)²

Ans: Using identity (x+y+z)² = x²+y²+z²+2xy+2yz+2zx
Here, x = 3a
y = – 7b
z = – c
(3a –7b– c)² = (3a)²+(– 7b)²+(– c)²+(2×3a ×– 7b)+(2×– 7b ×– c)+(2×– c ×3a)
= 9a² + 49b² + c²– 42ab+14bc–6ca

(v) (–2x + 5y – 3z)² 

Ans: Using identity, (x+y+z)²= x²+y²+z²+2xy+2yz+2zx
Here, x = –2x
y = 5y
z = – 3z
(–2x+5y–3z)² = (–2x)²+(5y)²+(–3z)²+(2×–2x × 5y)+(2× 5y×– 3z)+(2×–3z ×–2x)
= 4x²+25y² +9z²– 20xy–30yz+12zx

(vi)  ((1/4)a-(1/2)b+1)²

Ans: Using identity, (x+y+z)² = x²+y²+z²+2xy+2yz+2zx
Here, x = (1/4)a
y = (-1/2)b
z = 1

Q5: Factorise: 

(i) 4x² + 9y² + 16z² + 12xy – 24yz – 16xz
Ans: Using identity, (x+y+z)² = x²+y²+z²+2xy+2yz+2zx
We can say that, x²+y²+z²+2xy+2yz+2zx = (x+y+z)²
4x²+9y²+16z²+12xy–24yz–16xz = (2x)²+(3y)²+(−4z)²+(2×2x×3y)+(2×3y×−4z) +(2×−4z×2x)
= (2x+3y–4z)²
= (2x+3y–4z)(2x+3y–4z)

(ii) 2x² + y² + 8z² – 2√2xy + 4√2 yz – 8xz

Ans: Using identity, (x +y+z)² = x²+y²+z²+2xy+2yz+2zx
We can say that, x²+y²+z²+2xy+2yz+2zx = (x+y+z)²
2x²+y²+8z²–2√2xy+4√2yz–8xz
= (-√2x)²+(y)²+(2√2z)²+(2×-√2x×y)+(2×y×2√2z)+(2×2√2×−√2x)
= (−√2x+y+2√2z)₂
= (−√2x+y+2√2z)(−√2x+y+2√2z)

Q6: Write the following cubes in expanded form: 
(i) (2x + 1)³ 

Ans: Using identity,(x+y)³ = x³+y³+3xy(x+y)
(2x+1)3= (2x)³+13+(3×2x×1)(2x+1)
= 8x³+1+6x(2x+1)
= 8x³+12x²+6x+1

(ii) (2a – 3b)³ 

Ans: Using identity,(x–y)³ = x³–y³–3xy(x–y)
(2a−3b)³ = (2a)³−(3b)³–(3×2a×3b)(2a–3b)
= 8a³–27b³–18ab(2a–3b)
= 8a³–27b³–36a²b+54ab²

(iii)  ((3/2)x+1)³

Ans: Using identity,(x+y)³ = x³+y³+3xy(x+y)
((3/2)x+1)³=((3/2)x)³+13+(3×(3/2)x×1)((3/2)x +1)

(iv) (x−(2/3)y)³

Ans: Using identity, (x –y)³ = x³–y³–3xy(x–y)

Q7: Evaluate the following using suitable identities: 
(i) (99)³

Ans: We can write 99 as 100–1 
Using identity, (x –y)³ = x³–y³–3xy(x–y) 
(99)³ = (100–1)³ 
= (100)³–1³–(3×100×1)(100–1) 
= 1000000 –1–300(100 – 1) 
= 1000000–1–30000+300 
= 970299 
= 970299

(ii) (102)³

Ans: We can write 102 as 100+2 
Using identity,(x+y)³ = x³+y³+3xy(x+y) 
(100+2)³ =(100)³+2³+(3×100×2)(100+2)
= 1000000 + 8 + 600[100 + 2]
= 1000000 + 8 + 60000 + 1200
= 1061208

(iii) (998)³

Ans: We can write 99 as 1000–2 
Using identity,(x–y)³ = x³–y³–3xy(x–y) 
(998)³ =(1000–2)³ 
=(1000)³–2³–(3×1000×2)(1000–2) 
= 1000000000–8–6000(1000– 2) 
= 1000000000–8- 6000000+12000 
= 994011992 

Q8: Factorise each of the following:  
(i) 8a³ + b3 + 12a²b + 6ab² 

Ans: The expression, 8a³+b³+12a²b+6ab² can be written as (2a)³+b³+3(2a)²b+3(2a)(b)²
8a³+b³+12a²b+6ab² = (2a)³+b³+3(2a)²b+3(2a)(b)²
= (2a+b)³
= (2a+b)(2a+b)(2a+b)
Here, the identity, (x +y)³ = x³+y³+3xy(x+y) is used.

(ii) 8a³ – b³ – 12a²b + 6ab²

Ans: The expression, 8a³–b³−12a²b+6ab² can be written as (2a)³–b³–3(2a)²b+3(2a)(b)²
8a³–b³−12a²b+6ab² = (2a)³–b³–3(2a)²b+3(2a)(b)²
= (2a–b)³
= (2a–b)(2a–b)(2a–b)
Here, the identity,(x–y)³ = x³–y³–3xy(x–y) is used.

(iii) 27 – 125a³ – 135a + 225a² 

Ans: The expression, 27–125a³–135a +225a² can be written as 3³–(5a)³–3(3)²(5a)+3(3)(5a)²
27–125a³–135a+225a² =
33–(5a)³–3(3)²(5a)+3(3)(5a)²
= (3–5a)³
= (3–5a)(3–5a)(3–5a)
Here, the identity, (x–y)³ = x³–y³-3xy(x–y) is used.

(iv) 64a³ – 27b³ – 144 a²b + 108 ab² 

Ans: The expression, 64a³–27b³–144a²b+108ab² can be written as
(4a)³–(3b)³ – 3(4a)²(3b)+3(4a)(3b)²
64a³–27b³ – 144a²b+108ab²
= (4a)³–(3b)³–3(4a)²(3b)+3(4a)(3b)²
=(4a–3b)³
=(4a–3b)(4a–3b)(4a–3b)
Here, the identity, (x – y)³ = x³ – y³ – 3xy(x – y) is used.

(v) 27p³– (1/216)−(9/2) p²+(1/4)p

Ans: The expression, 27p³–(1/216)−(9/2) p²+(1/4)p can be written as 
(3p)³–(1/6)³−(9/2) p²+(1/4)p = (3p)³–(1/6)³−3(3p)(1/6)(3p – 1/6) 
Using (x – y)³ = x³ – y³ – 3xy (x – y) 
27p³–(1/216)−(9/2) p²+(1/4)p = (3p)³–(1/6)³−3(3p)(1/6)(3p – 1/6) 
Taking x = 3p and y = 1/6 
= (3p–1/6)³ 
= (3p–1/6)(3p–1/6)(3p–1/6) 

Q9: Verify: 
(i) x³+y³ = (x+y)(x²–xy+y²) 

Ans: We know that, (x+y)³ = x³+y³+3xy(x+y)
⇒ x³+y³ = (x+y)³–3xy(x+y)
⇒ x³+y³ = (x+y)[(x+y)²–3xy]
Taking (x+y) common ⇒ x³+y³ = (x+y)[(x²+y²+2xy)–3xy]
⇒ x³+y³ = (x+y)(x²+y²–xy)

(ii) x³–y³ = (x–y)(x²+xy+y²)  

Ans: We know that,(x–y)³ = x³–y³–3xy(x–y)
⇒ x³−y³ = (x–y)³+3xy(x–y)
⇒ x³−y³ = (x–y)[(x–y)²+3xy]
Taking (x+y) common ⇒ x³−y³ = (x–y)[(x²+y²–2xy)+3xy]
⇒ x³+y³ = (x–y)(x²+y2+xy)

 Q10: Factorise each of the following: 
(i) 27y³+125z³

Ans: The expression, 27y³+125z³ can be written as (3y)³+(5z)³
27y³+125z³ = (3y)³+(5z)³
We know that, x³+y³ = (x+y)(x²–xy+y2)
27y³+125z³ = (3y)³+(5z)³
= (3y+5z)[(3y)²–(3y)(5z)+(5z)²]
= (3y+5z)(9y²–15yz+25z²)

(ii) 64m³–343n³

Ans: The expression, 64m³–343n³can be written as (4m)³–(7n)³
64m³–343n³ = (4m)³–(7n)³
We know that, x³–y³ = (x–y)(x²+xy+y²)
64m³–343n³ = (4m)³–(7n)³
= (4m-7n)[(4m)²+(4m)(7n)+(7n)²]
= (4m-7n)(16m²+28mn+49n²)

Q11: Factorise 27x³ + y³ + z³ – 9xyz.

Solution: The expression27x³+y³+z³–9xyz can be written as (3x)³+y³+z³–3(3x)(y)(z)
27x³+y³+z³–9xyz  = (3x)³+y³+z³–3(3x)(y)(z)
We know that, x³+y³+z³–3xyz = (x+y+z)(x²+y²+z²–xy –yz–zx)
27x³+y³+z³–9xyz  = (3x)³+y³+z³–3(3x)(y)(z)
= (3x+y+z)[(3x)²+y²+z²–3xy–yz–3xz]
= (3x+y+z)(9x²+y²+z²–3xy–yz–3xz)

Q12: Verify that x³ + y³ + z³ – 3xyz = (1/2) (x + y + z)[(x – y)² + (y – z)² + (z – x)²]

Ans: We know that,
x³+y³+z³−3xyz = (x+y+z)(x²+y²+z²–xy–yz–xz)
⇒ x³+y³+z³–3xyz = (1/2)(x+y+z)[2(x²+y²+z²–xy–yz–xz)]
= (1/2)(x+y+z)(2x²+2y²+2z²–2xy–2yz–2xz)
= (1/2)(x+y+z)[(x²+y²−2xy)+(y²+z²–2yz)+(x²+z²–2xz)]
= (1/2)(x+y+z)[(x–y)²+(y–z)²+(z–x)²]

Q13: If x + y + z = 0, show that x³ + y³ + z³ = 3xyz.

Ans: We know that,
x³+y³+z³-3xyz = (x +y+z)(x²+y²+z²–xy–yz–xz)
Now, according to the question, let (x+y+z) = 0,
then, x³+y³+z³ -3xyz = (0)(x²+y²+z²–xy–yz–xz)
⇒ x³+y³+z³–3xyz = 0
⇒x³+y³+z³ = 3xyz
Hence Proved

Q14: Without actually calculating the cubes, find the value of each of the following: 
(i) (–12)³ + (7)³ + (5)³

Ans: Let a = −12
b = 7
c = 5
We know that if x+y+z = 0, then x³+y³+z³=3xyz.
Here, −12+7+5=0
(−12)³+(7)³+(5)³ = 3xyz
= 3×-12×7×5
= -1260

(ii) (28)³ + (–15)³ + (–13)³ 

Ans: Let a = 28
b = −15
c = −13
We know that if x+y+z = 0, then x³+y³+z³ = 3xyz.
Here, x+y+z = 28–15–13 = 0
(28)³+(−15)³+(−13)³ = 3xyz
= 0+3(28)(−15)(−13)
= 16380

Q15: Give possible expressions for the length and breadth of each of the following rectangles, in which their areas are given:
(i) Area : 25a²–35a+12

Ans: Using the splitting the middle term method,
We have to find a number whose sum = -35 and product =25×12=300
We get -15 and -20 as the numbers [-15+-20=-35 and -15×-20=300]
25a²–35a+12 = 25a²–15a−20a+12
= 5a(5a–3)–4(5a–3)
= (5a–4)(5a–3)
Possible expression for length  = 5a–4
Possible expression for breadth  = 5a –3

(ii) Area : 35y²+13y–12

Ans: Using the splitting the middle term method,
We have to find a number whose sum = 13 and product = 35×-12 = 420
We get -15 and 28 as the numbers [-15+28 = 13 and -15×28=420]
35y²+13y–12 = 35y²–15y+28y–12
= 5y(7y–3)+4(7y–3)
= (5y+4)(7y–3)
Possible expression for length  = (5y+4)
Possible expression for breadth  = (7y–3)

Q16: What are the possible expressions for the dimensions of the cuboids whose volumes are given below?
(i) Volume: 3x²–12x

Ans: 3x²–12x can be written as 3x(x–4) by taking 3x out of both the terms.
Possible expression for length = 3
Possible expression for breadth = x
Possible expression for height = (x–4)

(ii) Volume: 12ky²+8ky–20k

Ans: 12ky²+8ky–20k can be written as 4k(3y²+2y–5) by taking 4k out of both the terms.
12ky²+8ky–20k = 4k(3y²+2y–5)
[Here, 3y²+2y–5 can be written as 3y²+5y–3y–5 using splitting the middle term method.]
= 4k(3y²+5y–3y–5)
= 4k[y(3y+5)–1(3y+5)]
= 4k(3y+5)(y–1)
Possible expression for length = 4k
Possible expression for breadth = (3y +5)
Possible expression for height = (y -1)

Q1. Determine which of the following polynomials has (x + 1) a factor:
(i) x³ + x² + x + 1
Ans: Let p(x) = x³ + x² + x + 1
The zero of x + 1 is -1. [x + 1 = 0 means x = -1]
p(−1) = (−1)³ + (−1)² + (−1) + 1
= −1 + 1 − 1 + 1
= 0
∴ By factor theorem, x + 1 is a factor of x³ + x² + x + 1

(ii) x⁴ + x³ + x² + x + 1
Ans: Let p(x) =  x⁴ + x³ + x² + x + 1
The zero of x + 1 is -1. . [x + 1= 0 means x = -1]
p(−1) = (−1)4 + (−1)³ + (−1)² + (−1) + 1
= 1 − 1 + 1 − 1 + 1
= 1 ≠ 0
∴ By factor theorem, x+1 is not a factor of x⁴ + x³ + x² + x + 1

(iii) x⁴ + 3x³ + 3x² + x + 1 
Ans: Let p(x)= x⁴ + x³ + x² + x + 1
The zero of x+1 is -1.
p(−1)=(−1)⁴+3(−1)³+3(−1)²+(−1)+1
=1−3+3−1+1
=1 ≠ 0
∴ By factor theorem, x + 1 is not a factor of x⁴ +3x³ + 3x² + x + 1

(iv) x³ – x²– (2+√2)x +√2
Ans: Let p(x) = x³–x²–(2+√2)x +√2
The zero of x+1 is -1.
p(−1) = (-1)³–(-1)²–(2+√2)(-1) + √2 = −1−1+2+√2+√2
= 2√2 ≠ 0
∴ By factor theorem, x+1 is not a factor of x³–x²–(2+√2)x +√2

Q2. Use the Factor Theorem to determine whether g(x) is a factor of p(x) in each of the following cases:
(i) p(x) = 2x³ + x² – 2x – 1, g(x) = x + 1
Ans: p(x) = 2x³+x²–2x–1, g(x) = x+1
g(x) = 0
⇒ x+1 = 0
⇒ x = −1
∴ Zero of g(x) is -1.
Now,
p(−1) = 2(−1)³+(−1)²–2(−1)–1
= −2 + 1 + 2 − 1
= 0
∴ By factor theorem, g(x) is a factor of p(x).

(ii) p(x) = x³ + 3x² + 3x + 1, g(x) = x + 2
Ans: p(x) = x³+ 3x² 3x + 1, g(x) = x + 2
g(x) = 0
⇒ x + 2 = 0
⇒ x = −2
∴ Zero of g(x) is -2.
Now,
p(−2) = (−2)³+3(−2)²+3(−2)+1
= −8 + 12 − 6 + 1
= −1 ≠ 0
∴ By factor theorem, g(x) is not a factor of p(x).

(iii) p(x)= x³ – 4x² + x + 6, g(x) = x – 3
Ans: p(x) = x³– 4x² + x + 6, g(x) = x – 3
g(x) = 0
⇒ x−3 = 0
⇒ x = 3
∴ Zero of g(x) is 3.
Now,
p(3) = (3)³−4(3)² + (3) + 6
= 27 − 36 + 3 + 6
= 0
∴ By factor theorem, g(x) is a factor of p(x).

Q3. Find the value of k, if x–1 is a factor of p(x) in each of the following cases:
(i) p(x) = x² + x + k
Ans: If x – 1 is a factor of p(x), then p(1) = 0
By Factor Theorem
⇒ (1)²+(1)+k = 0
⇒ 1+1+k = 0
⇒ 2+k = 0
⇒ k = −2

(ii) p(x) = 2x² + kx + √2
Ans: If x-1 is a factor of p(x), then p(1)=0
⇒ 2(1)² + k(1) + √2 = 0
⇒ 2 + k + √2 = 0
⇒ k = −(2 + √2)

(iii) p(x) = kx²–√2x + 1
Ans: If x – 1 is a factor of p(x), then p(1)=0
By Factor Theorem
⇒ k(1)²-√2(1)+1=0
⇒ k = √2-1

(iv) p(x) = kx² – 3x + k
Ans: If x-1 is a factor of p(x), then p(1) = 0
By Factor Theorem
⇒ k(1)²–3(1)+k = 0
⇒ k−3+k = 0
⇒ 2k−3 = 0
⇒ k= 3/2

Q4. Factorize:
(i) 12x² – 7x + 1
Ans: Using the splitting the middle term method,
We have to find a number whose sum = -7 and product =1×12 = 12
We get -3 and -4 as the numbers [-3+-4=-7 and -3×-4 = 12]
12x²–7x+1= 12x²-4x-3x+1
= 4x(3x-1)-1(3x-1)
= (4x-1)(3x-1)

(ii) 2x² + 7x + 3
Ans: Using the splitting the middle term method,
We have to find a number whose sum = 7 and product = 2×3 = 6
We get 6 and 1 as the numbers [6+1 = 7 and 6×1 = 6]
2x²+7x+3 = 2x²+6x+1x+3
= 2x (x+3)+1(x+3)
= (2x+1)(x+3)

(iii) 6x² + 5x – 6 
Ans: Using the splitting the middle term method,
We have to find a number whose sum = 5 and product = 6×-6 = -36
We get -4 and 9 as the numbers [-4+9 = 5 and -4×9 = -36]
6x²+5x-6 = 6x²+9x–4x–6
= 3x(2x+3)–2(2x+3)
= (2x+3)(3x–2)

(iv) 3x²–x–4 
Ans: Using the splitting the middle term method,
We have to find a number whose sum = -1 and product = 3 × -4 = -12
We get -4 and 3 as the numbers [-4 + 3 = -1 and -4 × 3 = -12]
3x² – x – 4 = 3x² – x – 4
= 3x² – 4x + 3x – 4
= x(3x – 4) + 1(3x – 4)
= (3x – 4)(x + 1)

5. Factorize:
(i) x³– 2x² – x + 2
Ans: Let p(x) = x³–2x²–x+2
Factors of 2 are ±1 and ± 2
Now,
p(x) = x³–2x²–x+2
p(−1) = (−1)³–2(−1)²–(−1)+2
= −1−2+1+2
= 0
Therefore, (x+1) is the factor of p(x)

Now, Dividend = Divisor × Quotient + Remainder
Now by splitting the middle term method,
(x+1)(x²–3x+2) = (x+1)(x²–x–2x+2)
= (x+1)(x(x−1)−2(x−1))
= (x+1)(x−1)(x-2)

(ii) x³ – 3x² – 9x – 5
Ans: Let p(x) = x³–3x²–9x–5
Factors of 5 are ±1 and ±5
By trial method, we find that
p(5) = 0
So, (x-5) is factor of p(x)
Now,
p(x) = x³–3x²–9x–5
p(5) = (5)³–3(5)²–9(5)–5
= 125−75−45−5
= 0
Therefore, (x-5) is the factor of  p(x)

Now, Dividend = Divisor × Quotient + Remainder
(x−5)(x²+2x+1) = (x−5)(x²+x+x+1)
= (x−5)(x(x+1)+1(x+1))
= (x−5)(x+1)(x+1)

(iii) x³ + 13x² + 32x + 20
Ans: Let p(x) = x³+13x²+32x+20
Factors of 20 are ±1, ±2, ±4, ±5, ±10 and ±20
By trial method, we find that
p(-1) = 0
So, (x+1) is factor of p(x)
Now,
p(x)= x³+13x²+32x+20
p(-1) = (−1)³+13(−1)²+32(−1)+20
= −1+13−32+20
= 0
Therefore, (x+1) is the factor of p(x)

Now, Dividend = Divisor × Quotient +Remainder
Now by splitting the middle term method,
(x+1)(x²+12x+20) = (x+1)(x²+2x+10x+20)
= (x−5)x(x+2)+10(x+2)
= (x−5)(x+2)(x+10)

(iv) 2y³ + y² – 2y – 1
Ans: Let p(y) = 2y³+y²–2y–1
Factors = 2×(−1)= -2 are ±1 and ±2
By trial method, we find that
p(1) = 0
So, (y-1) is factor of p(y)
Now,
p(y) = 2y³+y²–2y–1
p(1) = 2(1)³+(1)²–2(1)–1
= 2+1−2
= 0
Therefore, (y-1) is the factor of p(y)

Now, Dividend = Divisor × Quotient + Remainder
Now by splitting the middle term method,
(y−1)(2y²+3y+1) = (y−1)(2y²+2y+y+1)
= (y−1)(2y(y+1)+1(y+1))
= (y−1)(2y+1)(y+1)

Q1. Find the value of the polynomial 5x – 4x² + 3 at 
(i) x = 0 
(ii) x = –1 
(iii) x = 2
Ans: 
Let f(x) = 5x−4x²+3
(i) When x = 0
f(0) = 5(0)-4(0)²+3
= 3

(ii) When x = -1
f(x) = 5x−4x²+3
f(−1) = 5(−1)−4(−1)²+3
= −5–4+3
= −6

(iii) When x = 2
f(x) = 5x−4x²+3
f(2) = 5(2)−4(2)²+3
= 10–16+3
= −3

Q2. Find p(0), p(1) and p(2) for each of the following polynomials: 
(i) p(y) = y² − y + 1
Ans: p(y) = y²–y+1
∴ p(0) = (0)²− (0) + 1 = 1
p(1) = (1)² – (1) + 1 =1
p(2) = (2)²–(2) + 1 = 3

(ii) p(t) = 2 + t + 2t² − t³
Ans:  p(t) = 2 + t + 2t² − t³
∴ p(0) = 2 + 0 + 2(0)² – (0)³ = 2
p(1) = 2 + 1 + 2(1)² – (1)³ = 2 + 1 + 2 – 1 = 4
p(2) = 2 + 2 + 2(2)² – (2)³ = 2 + 2 + 8 – 8 = 4

(iii) p(x) = x³
Ans: ∴ p(0) = (0)³ = 0
p(1) = (1)³ = 1
p(2) = (2)³ = 8

(iv) P(x) = (x − 1) (x + 1)
Ans: ∴ p(0) = (0 – 1)(0 + 1) = (−1)(1) = –1
p(1) = (1 – 1)(1 + 1) = 0(2) = 0
p(2) = (2 – 1)(2 + 1) = 1(3) = 3

Q3. Verify whether the following are zeroes of the polynomial, indicated against them.
(i) p(x) = 3x + 1, x = −1/3
Ans: For, x = -1/3, p(x) = 3x+1
∴ p(−1/3) = 3(-1/3)+1 = −1+1 = 0
∴ -1/3 is a zero of p(x).

(ii) p(x) = 5x – π, x = 4/5
Ans: For, x = 4/5, p(x) = 5x – π
∴ p(4/5) = 5(4/5) – π = 4  -π
∴ 4/5 is not a zero of p(x).

(iii) p(x) = x² − 1, x = 1, −1
Ans: For, x = 1, −1;
p(x) = x²−1
∴ p(1) = 1² − 1 = 1 − 1 = 0
p(−1) = (-1)² − 1 = 1 − 1 = 0
∴ 1, −1 are zeros of p(x).

(iv) p(x) = (x+1)(x–2), x =−1, 2
Ans: For, x = −1,2;
p(x) = (x+1)(x–2)
∴ p(−1) = (−1+1)(−1–2)
= (0)(−3) = 0
p(2) = (2+1)(2–2) = (3)(0) = 0
∴ −1,2 are zeros of p(x).

(v) p(x) = x², x = 0
Ans: For, x = 0 p(x) = x²
p(0) = 0² = 0
∴ 0 is a zero of p(x).

(vi) p(x) = lx + m, x = −m/l
Ans: For, x = -m/l ; p(x) = lx+m
∴ p(-m/l)= l(-m/l)+m = −m+m = 0
∴ -m/l is a zero of p(x).

(vii) p(x) = 3x²−1, x = -1/√3 , 2/√3
Ans: For, x = -1/√3 , 2/√3 ; p(x) = 3x²−1
∴ p(-1/√3) = 3(-1/√3)²-1 = 3(1/3)-1 = 1-1 = 0
∴ p(2/√3 ) = 3(2/√3)²-1 = 3(4/3)-1 = 4−1=3 ≠ 0
∴ -1/√3 is a zero of p(x) but 2/√3  is not a zero of p(x).

(viii) p(x) =2x + 1, x = 1/2
Ans: For, x = 1/2 p(x) = 2x + 1
∴ p(1/2) = 2(1/2) + 1 = 1 + 1 = 2 ≠ 0
∴ 1/2 is not a zero of p(x).

Q4. Find the zero of the polynomial in each of the following cases: 
(i) p(x) = x + 5 
Ans: p(x) = x + 5
⇒ x + 5 = 0
⇒ x = −5
∴ -5 is a zero polynomial of the polynomial p(x).

(ii) p(x) = x – 5
Ans: p(x) = x − 5
⇒ x − 5 = 0
⇒ x = 5
∴ 5 is a zero polynomial of the polynomial p(x).

(iii) p(x) = 2x + 5
Ans: p(x) = 2x + 5
⇒ 2x+5 = 0
⇒ 2x = −5
⇒ x = -5/2
∴ x = -5/2 is a zero polynomial of the polynomial p(x).

(iv) p(x) = 3x–2 
Ans: p(x) = 3x–2
⇒ 3x − 2 = 0
⇒ 3x = 2
⇒x = 2/3
∴ x = 2/3  is a zero polynomial of the polynomial p(x).

(v) p(x) = 3x 
Ans: p(x) = 3x
⇒ 3x = 0
⇒ x = 0
∴ 0 is a zero polynomial of the polynomial p(x).

(vi) p(x) = ax, a ≠ 0
Ans: p(x) = ax
⇒ ax = 0
⇒ x = 0
∴ x = 0 is a zero polynomial of the polynomial p(x).

(vii) p(x) = cx + d, c ≠ 0, c, d are real numbers.
Ans: p(x) = cx + d
⇒ cx + d =0
⇒ x = -d/c
∴ x = -d/c is a zero polynomial of the polynomial p(x).

Q1. Which of the following expressions are polynomials in one variable and which are not? State reasons for your answer.
(i) 4x²–3x+7
Ans: The equation 4x²–3x+7 can be written as 4x² – 3x¹ + 7x⁰
Since x is the only variable in the given equation and the powers of x (i.e., 2, 1 and 0) are whole numbers, we can say that the expression 4x² – 3x + 7 is a polynomial in one variable.

(ii) y²+√2
Ans: The equation y² + √2 can be written as y² + √2y⁰
Since y is the only variable in the given equation and the powers of y (i.e., 2 and 0) are whole numbers, we can say that the expression y² + √2 is a polynomial in one variable.

(iii) 3√t + t√2
Ans: The equation 3√t + t√2 can be written as 3t^1/2 + √2t
Though t is the only variable in the given equation, the powers of t (i.e.,1/2) is not a whole number. Hence, we can say that the expression 3√t + t√2 is not a polynomial in one variable.

(iv) y + 2/y
Ans: The equation y + 2/y can be written as y + 2y^-1
Though y is the only variable in the given equation, the powers of y (i.e.,-1) is not a whole number. Hence, we can say that the expression y + 2/y is not a polynomial in one variable.

(v) x¹⁰ + y³ + t⁵⁰
Ans: Here, in the equation x¹⁰ + y³ + t⁵⁰
Though the powers, 10, 3, 50, are whole numbers, there are 3 variables used in the expression
x¹⁰ + y³ + t⁵⁰.
Hence, it is not a polynomial in one variable.

Q2. Write the coefficients of x² in each of the following:
(i) 2 + x² + x
Ans: The equation 2 + x²+x can be written as 2 + (1)x² + x
We know that, coefficient is the number which multiplies the variable.
Here, the number that multiplies the variable x² is 1
the coefficients of x² in 2 + x² + x is 1.

(ii) 2 – x²  + x³
Ans: The equation 2 – x² + x³ can be written as 2 + (–1)x² + x³
We know that, coefficient is the number (along with its sign, i.e., – or +) which multiplies the variable.
Here, the number that multiplies the variable x² is -1 the coefficients of x² in 2 – x² + x³ is -1.

(iii) (π/2)x² + x
Ans: The equation (π/2)x² + x can be written as (π/2)x² + x
We know that, coefficient is the number (along with its sign, i.e., – or +) which multiplies the variable.
Here, the number that multiplies the variable x² is π/2.
the coefficients of x² in (π/2)x² +x is π/2.

(iv)√2x – 1
Ans: The equation √2x – 1 can be written as 0x²+√2x-1 [Since 0x² is 0]
We know that, coefficient is the number (along with its sign, i.e., – or +) which multiplies the variable.
Here, the number that multiplies the variable x² is 0, the coefficients of x² in √2x – 1 is 0.

Q3. Give one example each of a binomial of degree 35, and of a monomial of degree 100.
Ans: The degree of a polynomial is the highest power of the variable in the polynomial. It represents the highest exponent of the variable within the algebraic expression.
Therefore,

• Binomial of degree 35: A polynomial having two terms and the highest degree 35 is called a binomial of degree 35
  Example: 3x³⁵+5
• Monomial of degree 100: A polynomial having one term and the highest degree 100 is called a monomial of degree 100
  Example: 4x¹⁰⁰

Q4. Write the degree of each of the following polynomials:
(i) 5x³ +  4x²  + 7x
Ans: The highest power of the variable in a polynomial is the degree of the polynomial.
Here, 5x³ + 4x² + 7x = 5x³ + 4x² + 7x¹
The powers of the variable x are: 3, 2, 1
The degree of 5x³ + 4x² + 7x is 3 as 3 is the highest power of x in the equation.

(ii) 4 – y²
Ans: The highest power of the variable in a polynomial is the degree of the polynomial.
Here, in 4–y²,
The power of the variable y is 2
The degree of 4 – y² is 2 as 2 is the highest power of y in the equation.

(iii) 5t – √7
Ans: The highest power of the variable in a polynomial is the degree of the polynomial.
Here, in 5t–√7,
The power of the variable t is 1.
The degree of 5t–√7 is 1 as 1 is the highest power of y in the equation.

(iv) 3
Ans: The highest power of the variable in a polynomial is the degree of the polynomial.
Here, 3 = 3 × 1 = 3 × x⁰
The power of the variable here is: 0
The degree of 3 is 0.

Q5. Classify the following as linear, quadratic and cubic polynomials:
Ans: We know that,
Linear polynomial: A polynomial of degree one is called a linear polynomial.
Quadratic polynomial: A polynomial of degree two is called a quadratic polynomial.
Cubic polynomial: A polynomial of degree three is called a cubic polynomial.
(i) x² + x
Ans: The highest power of x² + x is 2
The degree is 2
Hence, x² + x is a quadratic polynomial

(ii) x – x³
Ans: The highest power of x–x³ is 3
The degree is 3
Hence, x–x³ is a cubic polynomial

(iii) y + y² + 4
Ans: The highest power of y+y²+4 is 2
The degree is 2
Hence, y+y²+4is a quadratic polynomial

(iv) 1 + x
Ans: The highest power of 1 + x is 1
The degree is 1
Hence, 1 + x is a linear polynomial.

(v) 3t
Ans: The highest power of 3t is 1
The degree is 1
Hence, 3t is a linear polynomial.

(vi) r²
Ans: The highest power of r² is 2
The degree is 2
Hence, r² is a quadratic polynomial.

(vii) 7x³
Ans: The highest power of 7x³ is 3
The degree is 3
Hence, 7x³ is a cubic polynomial.

Exercise 1.3

Q1. Write the following in decimal form and mention the kind of decimal expansion each has. 
(i) 36/100
Ans:

= 0.36 (Terminating)

(ii) 1/11
Ans:

(iii) 
Ans:


= 4.125 (Terminating)

(iv) 3/13 
Ans:

(v) 2/11 
Ans:

(vi) 329/400 
Ans:

= 0.8225 (Terminating)

Q2. You know that 1/7 = . Can you predict what the decimal expansions of 2/7, 3/7, 4/7, 5/7, and 6/7 are, without actually doing the long division? If so, how?
[Hint: Study the remainders while finding the value of 1/7 carefully.]
Ans:

Q3. Express the following in the form p/q, where p and q are integers and q ≠ 0.
(i)  
Ans:

Assume that  x = 0.666…
Then,10x = 6.666…
10x = 6 + x
9x = 6
x = 2/3

(ii)
Ans:

= (4/10) + (0.777/10)
Assume that x = 0.777…
Then, 10x = 7.777…
10x = 7 + x
x = 7/9
(4/10) + (0.777../10) = (4/10) + (7/90) ( x = 7/9 and x = 0.777…0.777…/10 = 7/(9 × 10) = 7/90)
= (36/90) + (7/90) = 43/90

(iii) 
Ans:

Assume that  x = 0.001001…
Then, 1000x = 1.001001…
1000x = 1 + x
999x = 1
x = 1/999

Q4. Express 0.99999…. in the form p/q . Are you surprised by your answer? With your teacher and classmates discuss why the answer makes sense.
Ans: Assume that x = 0.9999…..Eq (a)
Multiplying both sides by 10,
10x = 9.9999…. Eq. (b)
Eq.(b) – Eq.(a), we get
(10x = 9.9999)-(x = 0.9999…)
9x = 9
x = 1
The difference between 1 and 0.999999 is 0.000001 which is negligible.
Hence, we can conclude that, 0.999 is very close to 1, therefore, 1 as the answer can be justified.

Q5. What can the maximum number of digits be in the repeating block of digits in the decimal expansion of 1/17? Perform the division to check your answer.
Ans: 1/17
Dividing 1 by 17:


There are 16 digits in the repeating block of the decimal expansion of 1/17.

Q6. Look at several examples of rational numbers in the form p/q (q ≠ 0), where p and q are integers with no common factors other than 1 and having terminating decimal representations (expansions). Can you guess what property q must satisfy?
Ans: We observe that when q is 2, 4, 5, 8, 10… Then the decimal expansion is a terminating one.
For example:
1/2 = 0. 5, denominator q = 2¹
7/8 = 0. 875, denominator q =2³
4/5 = 0. 8, denominator q = 5¹
We can observe that the terminating decimal may be obtained in the situation where prime factorization of the denominator of the given fractions has the power of only 2 or only 5 or both.

Q7. Write three numbers whose decimal expansions are non-terminating and non-recurring.
Ans: We know that all irrational numbers are non-terminating non-recurring. three numbers with decimal expansions that are non-terminating and non-recurring are:

• √3 = 1.732050807568
• √26 =5.099019513592
• √101 = 10.04987562112

Q8. Find three different irrational numbers between the rational numbers 5/7 and 9/11.
Ans:

Three different irrational numbers are:

• 0.73073007300073000073…
• 0.75075007300075000075…
• 0.76076007600076000076…

Q9. Classify the following numbers as rational or irrational according to their type:
(i)√23
Ans: √23 = 4.79583152331…
Since the number is non-terminating and non-recurring, therefore, it is an irrational number.

(ii)√225
Ans: √225 = 15 = 15/1
Since the number can be represented in p/q form, it is a rational number.

(iii) 0.3796
Ans: Since the number, 0.3796, is terminating, it is a rational number.

(iv) 7.478478
Ans: The number, 7.478478, is non-terminating but recurring, it is a rational number.

(v) 1.101001000100001…
Ans: Since the number, 1.101001000100001…, is non-terminating non-repeating (non-recurring), it is an irrational number.

Exercise 1.4

Q1. Classify the following numbers as rational or irrational:
(i) 2 –√5
Ans: We know that, √5 = 2.2360679…
Here, 2.2360679…is non-terminating and non-recurring.
Now, substituting the value of √5 in 2 –√5, we get,
2-√5 = 2-2.2360679… = -0.2360679
Since the number, – 0.2360679…, is non-terminating non-recurring, 2 –√5 is an irrational number.

(ii) (3 +√23)- √23
Ans: (3 +√23) –√23 = 3+√23–√23
= 3
= 3/1
Since the number 3/1 is in p/q form, (3 +√23)- √23 is rational.

(iii) 2√7/7√7
Ans: 2√7/7√7 = ( 2/7) × (√7/√7)
We know that (√7/√7) = 1
Hence, ( 2/7) × (√7/√7) = (2/7) × 1 = 2/7
Since the number, 2/7 is in p/q form, 2√7/7√7 is rational.

(iv) 1/√2
Ans: Multiplying and dividing the numerator and denominator by √2 we get,
(1/√2) × (√2/√2)= √2/2 ( since √2 × √2 = 2)
We know that, √2 = 1.4142…
Then, √2/2 = 1.4142/2 = 0.7071..
Since the number 0.7071..is non-terminating and non-recurring, 1/√2 is an irrational number.

(v) 2
Ans: We know that, the value of = 3.1415
Hence, 2 = 2 × 3.1415.. = 6.2830…
Since the number, 6.2830…, is non-terminating and non-recurring, 2 is an irrational number.

Q2. Simplify each of the following expressions:
(i) (3 + √3) (2 + √2)
Ans: (3 + √3) (2 + √2 )
Opening the brackets, we get, (3 × 2) + (3 × √2) + (√3 × 2) + (√3 × √2)
= 6 + 3√2 + 2√3 + √6

(ii) (3 + √3) (3 – √3)
Ans: (3 + √3) (3 – √3 ) = 3² – (√3)² = 9 – 3
= 6

(iii) (√5 + √2)²
Ans: (√5 + √2)² = √5² + (2 × √5 × √2) + √2²
= 5 + 2 × √10 + 2 = 7 + 2√10

(iv) (√5 – √2)(√5 + √2)
Ans: (√5 – √2)(√5 + √2) = (√5² – √2²) = 5 – 2 = 3

Q3. Recall, π is defined as the ratio of the circumference (say c) of a circle to its diameter, (say d). That is, π = c/d. This seems to contradict the fact that π is irrational. How will you resolve this contradiction?
Ans: There is no contradiction.
When we measure a value with a scale, we only obtain an approximate value.
We never obtain an exact value.
Therefore, we may not realize whether c or d is irrational.
The value of π is almost equal to 22/7 or 3.142857…

Q4. Represent (√9.3) on the number line.
Ans: 
Step 1: Draw a 9.3-unit long line segment, AB. Extend AB to C such that BC = 1 unit.
Step 2: Now, AC = 10.3 units. Let the centre of AC be O.
Step 3: Draw a semi-circle of radius OC with centre O.
Step 4: Draw a BD perpendicular to AC at point B intersecting the semicircle at D. Join OD.
Step 5: OBD, obtained, is a right-angled triangle.
Here, OD 10.3/2 (radius of semi-circle), OC = 10.3/2 , BC = 1
OB = OC – BC
⟹ (10.3/2)-1 = 8.3/2
Using Pythagoras theorem,
We get,
OD² = BD² + OB²
⟹ (10.3/2)² = BD²+(8.3/2)²
⟹ BD^{2 =} (10.3/2)²-(8.3/2)²
⟹ (BD)² = (10.3/2)-(8.3/2)(10.3/2)+(8.3/2)
⟹ BD² = 9.3
⟹ BD =  √9.3
Thus, the length of BD is √9.3.
Step 6: Taking BD as the radius and B as the centre draw an arc which touches the line segment.
The point where it touches the line segment is at a distance of √9.3 from O as shown in the figure.

Q5. Rationalize the denominators of the following:
(i) 1/√7
Ans: Multiply and divide 1/√7 by √7
(1×√7)/(√7×√7) = √7/7

(ii) 1/(√7-√6)
Ans: Multiply and divide 1/(√7 – √6) by (√7 + √6)
[1/(√7 – √6)] × (√7 + √6)/(√7 + √6) = (√7 + √6)/(√7 – √6)(√7 + √6)
= (√7 + √6)/√7² – √6² [denominator is obtained by the property, (a + b)(a – b) = a² – b²]
= (√7 + √6)/(7 – 6)
= (√7 + √6)/1
= √7 + √6

(iii) 1/(√5+√2)
Ans: Multiply and divide 1/(√5 + √2) by (√5 – √2)
[1/(√5 + √2)] × (√5 – √2)/(√5 – √2) = (√5 – √2)/(√5 + √2)(√5 – √2)
= (√5 – √2)/(√5² – √2²) [denominator is obtained by the property, (a + b)(a – b) = a² – b²]
= (√5 – √2)/(5 – 2)
= (√5 – √2)/3

(iv) 1/(√7-2)
Ans: Multiply and divide 1/(√7 – 2) by (√7 + 2)
1/(√7 – 2) × (√7 + 2)/(√7 + 2) = (√7 + 2)/(√7 – 2)(√7 + 2)
= (√7 + 2)/(√7² – 2²) [denominator is obtained by the property, (a + b)(a – b) = a²-b²]
= (√7 + 2)/(7 – 4)
= (√7 + 2)/3

Exercise 1.5

Q1. Find:

(i) 64^1/2

Ans: 64^1/2 = (8 × 8)^1/2
= (8²)^½
= 8¹ [⸪2 × 1/2 = 2/2 = 1]
= 8

(ii) 32^1/5
Ans: 32^1/5 = (2⁵)^1/5
= (2⁵)^⅕
= 2¹ [⸪ 5 × 1/5 = 1]
= 2

(iii) 125^1/3
Ans: (125)^1/3 = (5 × 5 × 5)^1/3
= (5³)^⅓
= 5¹ (3 × 1/3 = 3/3 = 1)
= 5

Q2. Find:
(i) 9^3/2
Ans: 9^3/2 = (3 × 3)^3/2
= (3²)^3/2
= 3³ [⸪ 2 × 3/2 = 3]
=27

(ii) 32^2/5
Ans: 32^2/5 = (2 × 2 × 2 × 2 × 2)^2/5
= (2⁵)^2⁄5
= 2² [⸪ 5 × 2/5= 2]
= 4

(iii)16^3/4
Ans: 16^3/4 = (2 × 2 × 2 × 2)^3/4
= (2⁴)^3⁄4
= 2³ [⸪ 4 × 3/4 = 3]
= 8

(iv) 125^-1/3
Ans: 125^-1/3 = (5 × 5 × 5)^-1/3
= (5³)^-1⁄3
= 5^-1 [⸪ 3 × -1/3 = -1]
= 1/5

Q.3. Simplify:
(i) 2^2/3×2^1/5
Ans: 2^2/3 × 2^1/5 = 2^(2/3)+(1/5) [⸪Since, a^m × aⁿ= a^m+n____ Laws of exponents]
= 2^13/15 [⸪ 2/3 + 1/5 = (2 × 5 + 3 × 1)/(3 × 5) = 13/15]

(ii) (1/3³)⁷
Ans: (1/3³)⁷ = (3^-3)⁷ [⸪Since,(a^m)ⁿ = a^{m x n}____ Laws of exponents]
= 3^-21

(iii) 11^1/2/11^1/4
Ans: 11^1/2/11^1/4 = 11^(1/2)-(1/4)
= 11^1/4 [⸪(1/2) – (1/4) = (1×4-2×1)/(2×4) = 4-2)/8 = 2/8 = ¼ ]

Oo
(iv) 7^1/2× 8^1/2
Ans: 7^1/2× 8^1/2 = (7 × 8)^1/2 [⸪ Since, (a^m × b^m = (a × b)^m ____ Laws of exponents]
= 56^1/2