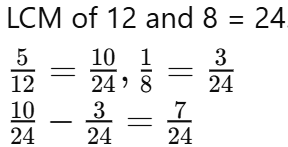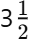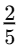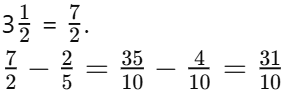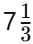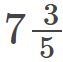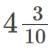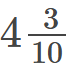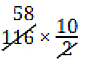Q1: The substances used to test whether a substance is acidic or basic are known as ________
Ans: The substances used to test whether a substance is acidic or basic are known as Indicators
Q2: Name the most commonly used indicator.
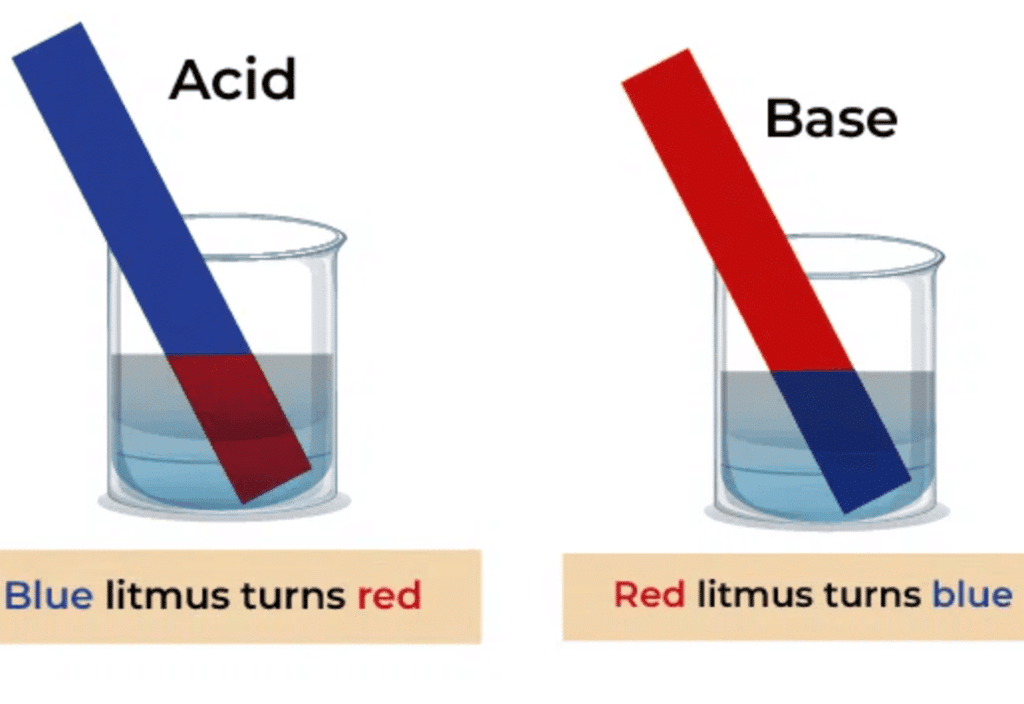
Ans: Litmus paper
Q3: From where do we extract litmus to be used as an indicator?
Ans: Lichens
Q4: In acidic solution, litmus paper turns into ______
Ans: In acidic solution, litmus paper turns into Red
Litmus paper is a pH indicator that turns red in acidic solutions, indicating the presence of acids.
Q5: In basic solution, litmus paper turns into ____
Ans: In basic solution, litmus paper turns into Blue
Litmus paper changes to blue in basic solutions, indicating the presence of bases.
Q6: In distilled water, litmus paper turns into _________
Ans: In distilled water, litmus paper turns into purple
Litmus paper remains purple in neutral distilled water, as it is neither acidic nor basic.
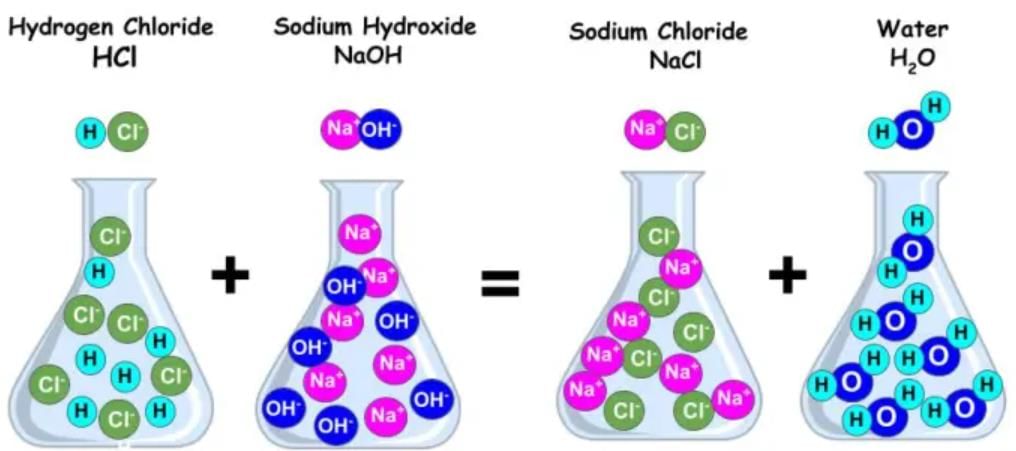
Q7: The reaction between an acid and a base is known as _________
Ans: The reaction between an acid and a base is known as neutralization.
Neutralization is the chemical reaction that occurs when an acid and a base react to form water and a salt.
Q8: Red rose indicator turns acidic solutions _______
a. Dark pink
b. Purple
c. Blue
d. None of these
Ans: a. Dark pink
China rose indicator changes to dark pink in acidic solutions, indicating their acidic nature.
Q9: Red/ China rose indicator turns basic solutions to ______
a. Dark pink
b. Purple
c. Blue
d. Green
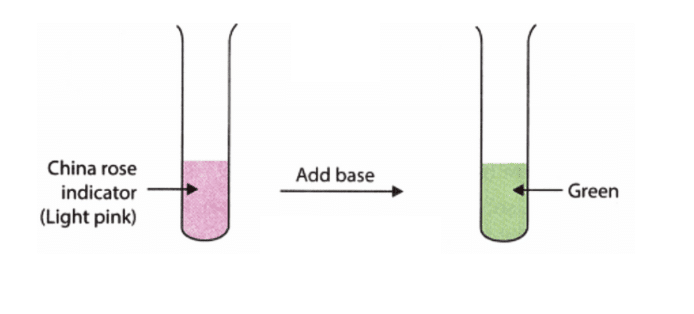
Ans: d. Green
The China rose indicator changes the colour of basic solutions to green.
In contrast, it turns acidic solutions to dark pink.
Q10: Salt and water are produced in the neutralization process with the evolution of ____________
Ans: Salt and water are produced in the neutralization process with the evolution of Heat
Q11: Name the acid present in our stomach.
Ans: HCL is present in our stomach.
Hydrochloric acid helps break down food and activates digestive enzymes, facilitating the digestion process.
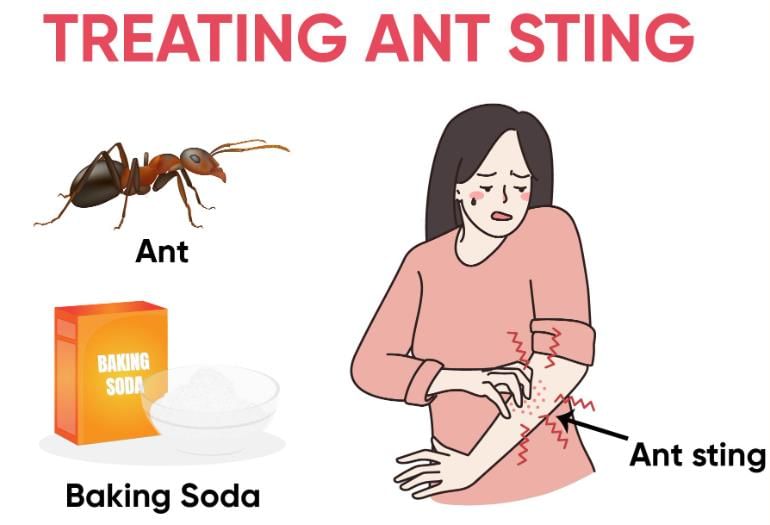
Q12: Name the acid present in the sting of an ant.
Ans: Formic acid is present in the sting of an ant.
Q13: State the nature of the soap solution.
Ans: Basic
Q14: State the nature of baking soda.
Ans: Basic
Q15: State the nature of lemon juice.
Ans: Acidic
Q16: Why does lemon juice and orange juice taste sour?
Ans: Because they contain acids.
Q17: Why does baking soda taste bitter?
Ans: Because it is basic in nature.
Q18: State one property of acids.
Ans: Acids are sour in taste.
Q19: State one property of bases.
Ans: Bases are bitter in taste.
Q20: Tina rubs a solution between her fingers and feels soapy; what is the nature of that solution?
Ans: Basic
Q21: Complete the following reaction:
HCl + NaOH —-> ______ + H2O
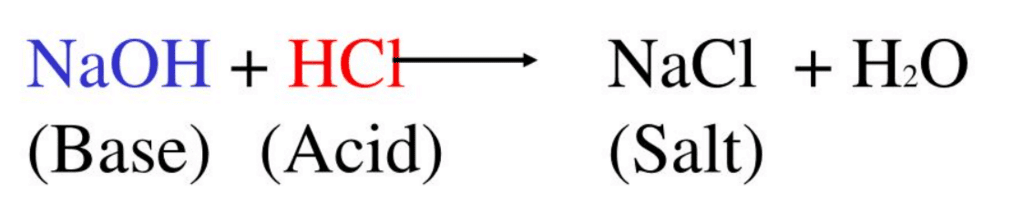
Ans: NaCl
Q22: Ammonia is found in many household products, such as window cleaners. It turns red litmus blue. Its nature _______________
Ans: Ammonia is found in many household products, such as window cleaners. It turns red litmus blue. Its nature is Basic
Q23: The wastes of many factories contain____________
Ans: The wastes of many factories contain Acids
Q24: Blue litmus paper is dipped in a solution. It remains blue, what is the nature of the solution?
Ans: Basic
Q25: Hydrogen ion is common to all acids. True/False
Ans: True
Q26: Name a base that is also used in soda acid fire extinguishers.
Ans: Baking soda.
Q27: Aqueous solution of acid conducts electricity due to ______________ present in it.
Ans: ion
Q28: Define pH.
Ans: pH is the measure of the Acidity or Alkalinity of a solution. The term pH stands for a negative log of hydrogen ion concentration.
Q29: The bases that dissolve in water are known as alkalies. True/ False.
Ans: True
Q30: Phenolphthalein becomes colourless in __________ and pink in_________.
Ans: Colourless in acid and pink in base.
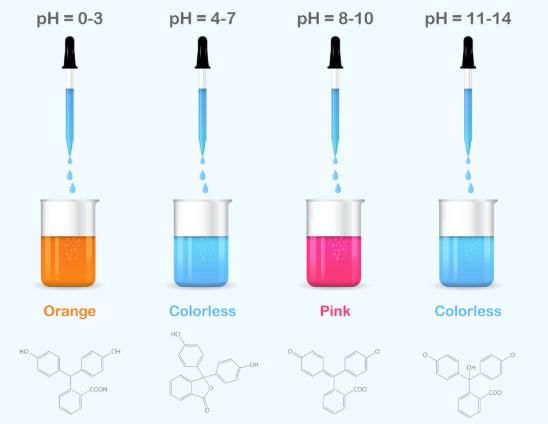
PhenolphthaleinQ31: Name the acid present in vinegar.
Ans: Acetic acid
Q32: Name the acid present in lemon.
Ans: citric acid
Q33: Change of colour in an acid or base depends on
a. Type of indicator
b. The acidic property of that substance
c. Basic property of that substance
d. None of these
Ans: Type of indicator
Q34: Name the acid present in curd.
Ans: Lactic acid