Page No. 92-93
Weaving Mats
You may have seen woven baskets of different kinds. If you look closely, you will notice different weaving patterns on each basket.
We will try weaving some mats with paper strips.
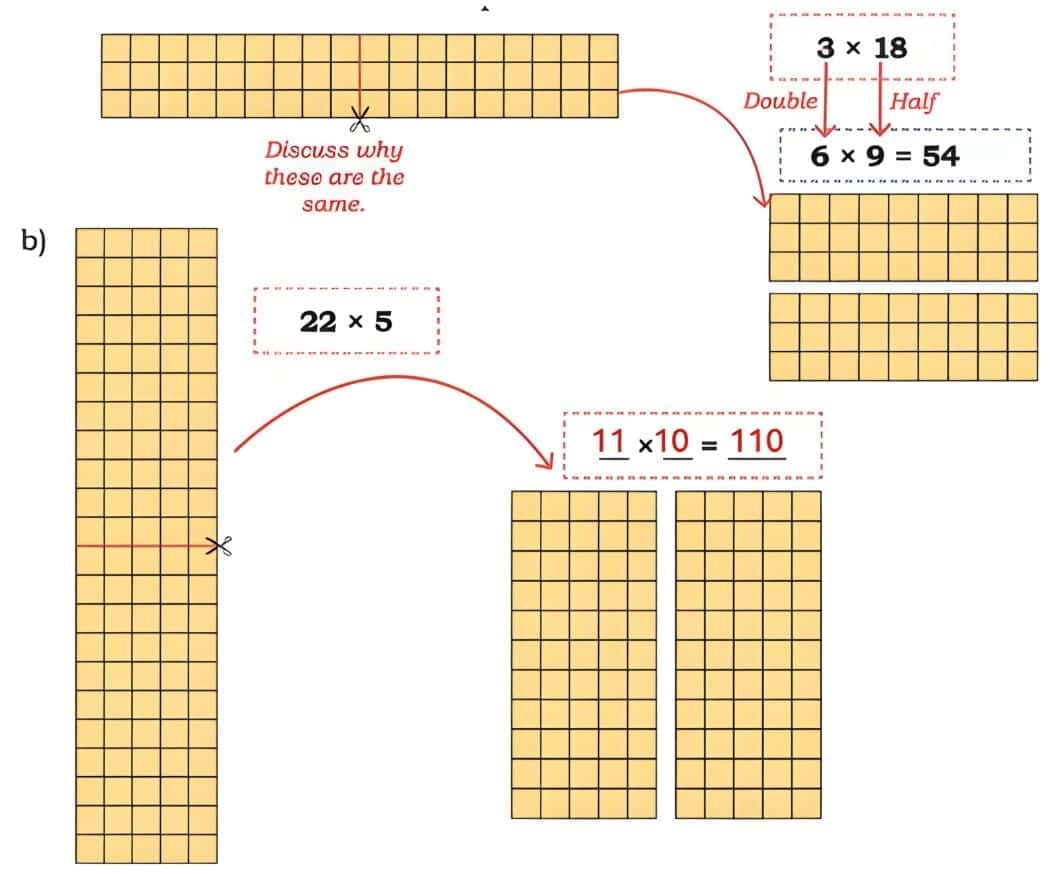
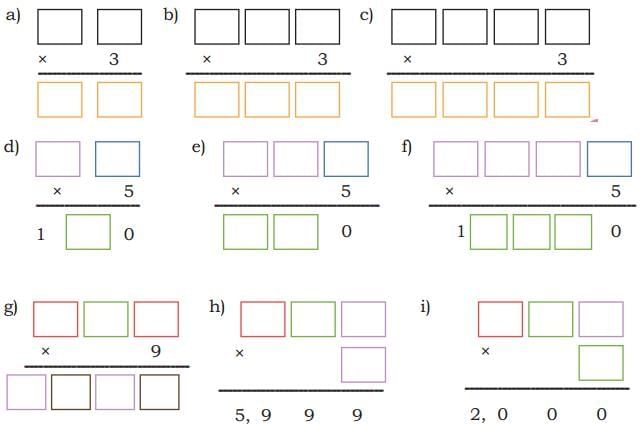
Q1: Let us make paper mats.
You will need —A coloured paper (30 cm long and 20 cm wide) and eight paper strips of two different colours (3 cm wide and longer than 20 cm).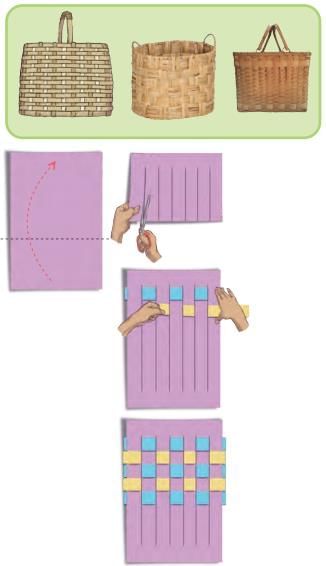 Ans:
Ans:
(a) Take a coloured paper 30 cm long and 20 cm wide.
(b) Fold the coloured paper in half along the longer side.
(c) Draw vertical lines at equal distances from the folded edge and cut slits leaving a gap of 3 cm at the top.
(d) Carefully unfold the paper. There will be no cuts in the paper at the top and the bottom.
(e) Now cut 8 paper strips of 3 cm width in 2 colours and of length slightly longer than 20 cm.
(f) Take one colour strip and weave it across the slits going one under and one over, and again one under and one over. Repeat it for the first row.
(g) Take one more strip of another colour and weave it across the slits going 1 over and one under, and again one over and one under. Repeat it for the second row.
(h) Weave all the strips in the same alternating pattern. Neatly fold any extra strip ends behind the mat. Your mat is ready!
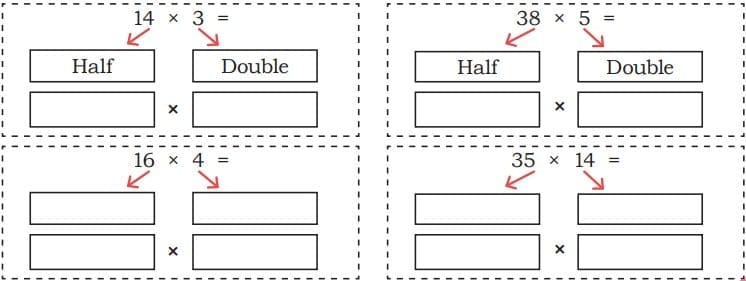
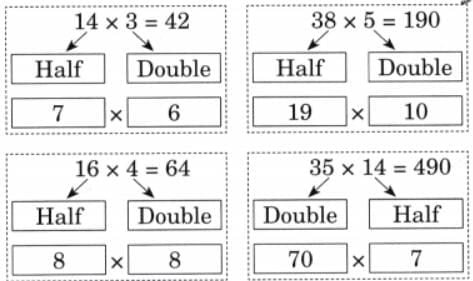
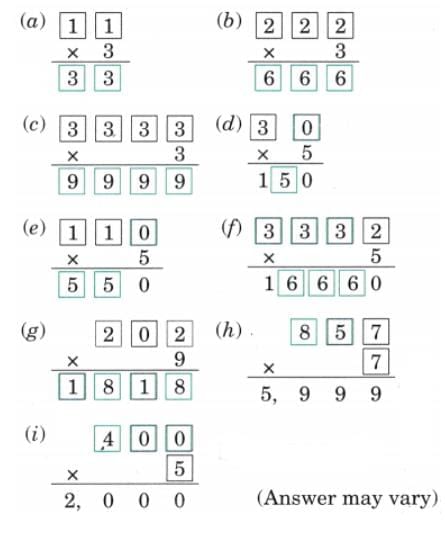
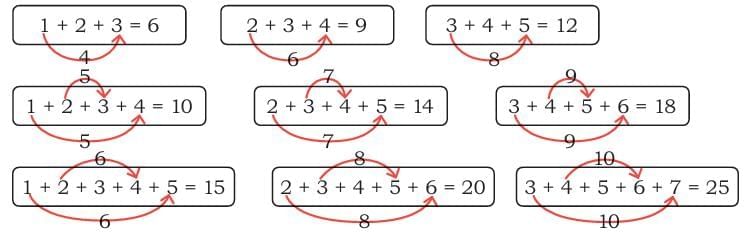
Q2: Can you work out the steps for any of these designs and weave the pattern?
Write the steps of the pattern in your notebook for each row until it starts repeating.
Ans:
For Image 1:
Row 1: 1 under (do not repeat), 3 over, 3 under, 3 over, … (repeat).
Row 2: 3 over, 3 under, 3 over, 3 under, 3 over, … (repeat).
Row 3: 2 over (do not repeat), 3 under, 3 over, 3 under, 3 over, … (repeat).
Row 4: 2 under (do not repeat), 3 over, 3 under, 3 over, … (repeat).
Row 5: 3 under, 3 over, 3 under, 3 over, … (repeat).
Row 6:1 over (do not repeat), 3 under, 3 over, 3 under, … (repeat).
For Image 2:
Row 1: 1 under, 3 over, 1 under, 3 over, 1 under, … (repeat).
Row 2: 2 under (do not repeat), 1 over, 3 under, 1 over, 3 under, 1 over, … (repeat).
Row 3: 1 over, 3 under, 1 over, 3 under, 1 over, … (repeat).
Row 4: 2 over (do not repeat), 1 under, 3 over, 1 under, … (repeat).
Row 5: 1 under, 3 over, 1 under, 3 over, 1 under, … (repeat).
Row 6: 2 under (do not repeat), 1 over, 3 under, 1 over, 3 under, … (repeat)
Let Us Try
Draw the following pattern on a grid paper. Part of it is done for you.
Now, complete the rest of the grid to get the full design.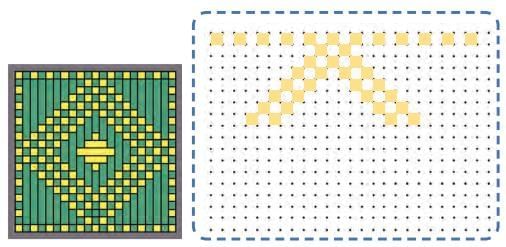 Ans:
Ans:
Do it yourself.
Page No. 94-99
Find Out
Q: Can squares (a regular 4-sided shape) fit together around a point without any gap or overlap? Try it out using cutouts of squares (a sample square is given at the end of the book). How many squares did you need?
Ans:
Yes, squares can fit around a point without leaving any gap or overlap.
The total angle around a point is 360°, and the corner angle of a square is 90°.
360° ÷ 90° = 4.
So, exactly four squares fit around a point.
Q: Can five squares fit together around a point without any gaps or overlaps? Why or why not?
Ans:
No, five squares cannot fit together around a point without gaps or overlaps. This is because the angle at each corner of a square is 90° and 5 × 90°= 450°.
Since 450° is greater than 360°, five squares will overlap and cannot fit neatly around a point.
Q: Can regular hexagons (6-sided shapes with equal sides) fit together around a point without any gaps or overlaps? Try and see (a sample hexagon is given at the end of the book). How many fit together at a point?
Ans:
Yes, regular hexagons can fit together around a point without any gaps or overlaps.
The angle at each corner of a regular hexagon is 120°, and the total angle around a point is 360°.
360° ÷ 120° = 3.
So, 3 hexagons fit together perfectly around a point.
Q: Here is a tessellating pattern with more than one shape.
What shapes have been used in this pattern?
Ans:
Equilateral triangles and regular hexagons used in the above pattern.
Q: Continue the pattern given below and colour it appropriately.
Ans:
Do it yourself.
Q: Do regular octagons fit together without any gaps or overlaps? Try drawing the same and check.
Ans:
No, regular octagons do not fit together perfectly without any gaps or overlaps to form a tessellation.
Q: Look at the pattern given below. What shapes are coming together at the marked points? Are the same set of shapes coming together at these points? Continue the pattern and colour it appropriately.
Ans:
At each marked point, two octagons and one square come together.
Yes, the same set of shapes (two octagons and one square) meet at all the red-marked points.
Q: Here is a tiling pattern made using two different shapes-squares and triangles. Are the triangles equilateral? Why or why not?
What shapes are coming together at the marked points?
Are the same set of shapes coming together at these points? Continue the pattern and colour it appropriately.
Ans: Since the sides of the squares used in the tiling pattern are equal, the sides of the triangles used to fill in the gaps between the squares must be equal. Thus, the triangles are equilateral.
At each marked point, two squares and one equilateral triangle are coming together.
Yes, the same set of shapes are coming together at all marked points.
Q: What geometrical shapes can you make by fitting 2 of these triangles together? Trace the shapes you created.Ans:
Q1: How many different types of triangles can you make?
Ans: 4, isosceles triangle, scalene triangle, equilateral triangle and right triangle.
Q2: Is it possible to make a triangle where all three sides are equal (equilateral triangle)?
Ans:
Yes, it is possible to make a triangle where all three sides are equal. Such a triangle is called an equilateral triangle.
Q3: Is it possible to make a triangle where all three sides are unequal?
Ans: Yes, it is possible to make a triangle where all three sides are unequal. Such a triangle is called a scalene triangle.
Q4: How many different 4-sided shapes (quadrilaterals) can you make?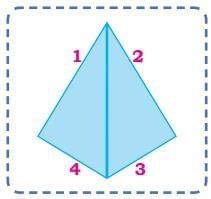 Here are three possible shapes.
Here are three possible shapes.
Have you made a shape like the one shown on the right?
Ans:
A rectangle, a kite, and a parallelogram are the three 4-sided shapes that can be made.
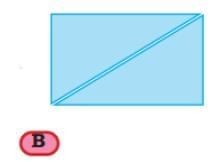
Q5: Measure the sides of each of these two quadrilaterals A and B. What do you notice?
Are there any pairs of sides that are equal? Which pairs are equal—adjacent or opposite?
Ans: On measuring, it is found that the opposite sides of the quadrilaterals A and B are equal.
Q6: In the grid given below, draw two different kites and parallelograms each.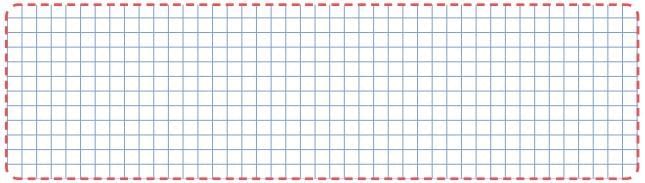 Ans:
Ans:
Do it yourself.
Q7: Now, use 3 triangles from the rhombus to form shapes. How many sides do each one of them have?
Using 3 triangular pieces of the rhombus, try creating a (a) 3-sided shape, (6) 4-sided shape, and (c) 5-sided shape.
Ans:
Do it yourself.
Q8: Which of these shapes can be made with all 4 pieces? Try and find out.
(a) Square
(b) Rectangle
(c) Triangle
(d) Pentagon (5-sided)
(e) Hexagon (6-sided)
(f) Octagon (8-sided)
Ans:
(a) Square
If you divide a rhombus into four triangles using its diagonals, you get four identical right triangles. With these four pieces:
(a) Square: Not possible (unless the rhombus was already a square).
(b) Rectangle: Possible. Two triangles can form a rectangle, and combining two rectangles gives a larger rectangle.
(c) Triangle: Not possible—four pieces cannot be arranged into a perfect triangle.
(d) Pentagon (5-sided): Cannot be formed.
(e) Hexagon (6-sided): Possible, by arranging the four triangles with their hypotenuses facing outward.
(f) Octagon (8-sided): Not possible with just four pieces.
Tangram
Q: Look at the tangram set given at the end of your textbook. Cut out all the shapes. Name them.
(a) How are they same or different from each other?
(b) What do you notice about the angles of each of the shapes?
(c) What do you notice about the sides of each of the shapes? Ans:
Ans:
(a) Shape 1, 2, 3, 5 and 6 are triangles. Out of these shapes 2 and 3 are equal and shapes 1 and 5 are equal. Shape 4 is a square and shape 7 is a parallelogram.
(b) In shape 2, 3 and 6 only two angles are equal where as in shape 1, 5 and 4 all angles are equal. In shape 7 opposite angles are equal.
(c) In shape 2, 3 and 6 only two sides are equal where as in shape 1, 5 and 4 all sides are equal. In shape 7 opposite sides are equal.
Page No. 100
Which Shape Am I?
Q: Match the statements with appropriate shapes. Do some of them describe more than one shape?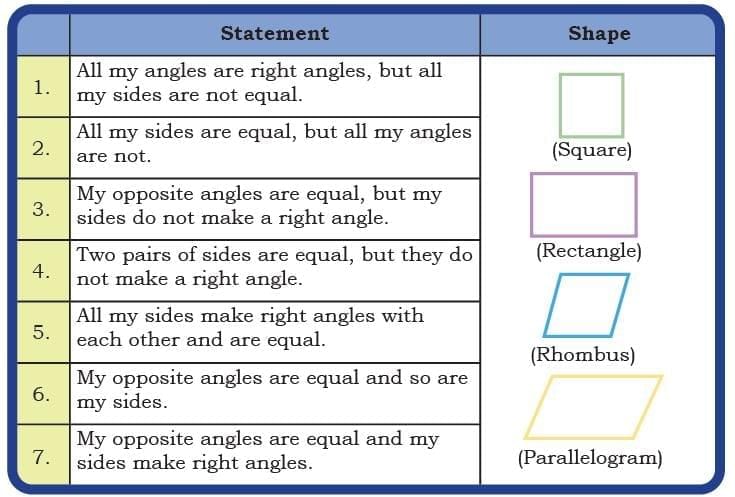 Ans:
Ans: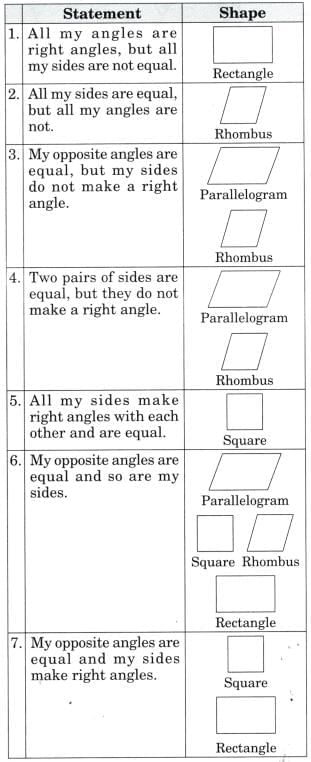
Kites
Make your own kite shape.
(a) Start with a square piece of paper.
(b) Take one corner of the paper and fold it towards the opposite corner, creating a sharp crease along the diagonal.
(c) Open and fold the corner A inwards, aligning the edge with the crease you just made.
(d) Repeat on the other side, folding the other corner B inwards to align with the crease at the centre.
You have a kite shape!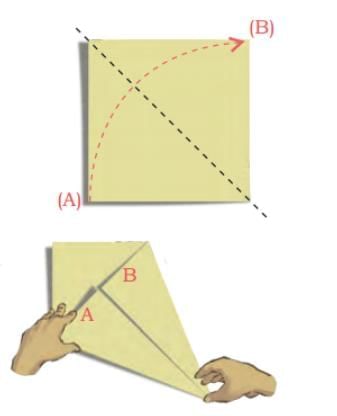 Q: What shapes do you see in the kite?
Q: What shapes do you see in the kite?
Ans:
Three right-angled triangle in which two are of same size.
Page No. 101
Play with Circles
Do you remember a circle?
(a) Draw a circle with a compass and mark its centre.
(b) Draw its diameter. Mark the endpoints of the diameter.
(c) Draw another diameter of the circle and mark the endpoints.
(d) Now join the four points.
What shape is formed? Check the sides of the quadrilateral and the angles obtained.
Ans: The opposite sides and angles are equal. All angles are right angles.
Try with a different pair of diameters.
What do you notice about the shape that is formed?
Ans: Everytime we get a rectangle.
Is it possible to create a 4-sided shape other than a rectangle through this process?
Ans: We can create a rectangle only with this process.
Page No. 102
Cube Connections
Q1: Here are three views of a cube. Can you draw them on the net in the correct order?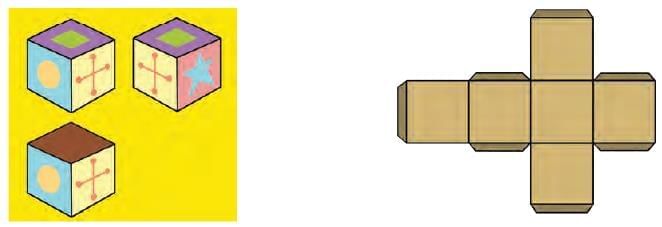 Ans:
Ans: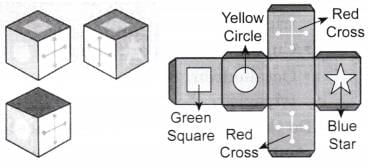
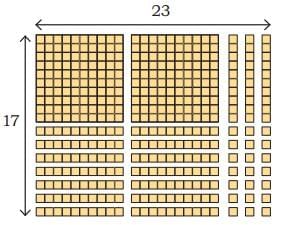
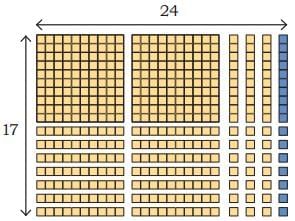
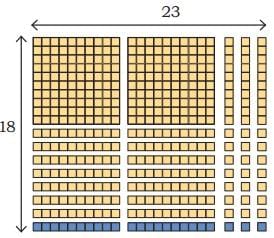
Q2: Here are some big solid cube frames. How many small cubes have been removed from each cube?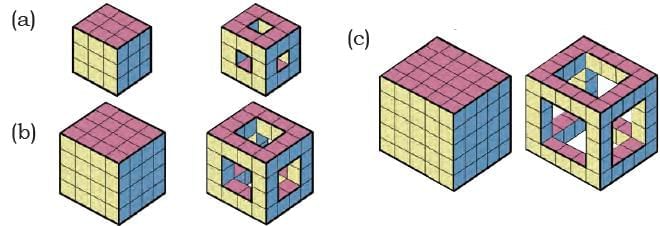
Ans:
(a) The full cube has 3 × 3 × 3 = 27 small cubes.
After removing the small cubes only the big cube frame has 20 small cubes. So, total removed cubes = 27-20 = 7 cubes.
(b) The full cube has 4 × 4 × 4 = 64 small cubes.
After removing the small cubes the big cube frame has 32 small cubes.
So, total removed cubes = 64 – 32
= 32 cubes.
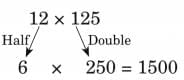
(c) The full cube has 5 × 5 × 5 = 125 small cubes.
After removing the small cubes the big cube frame has 44 small cubes.
So, total removed cubes = 125 – 44
= 81 cubes.
Q3: Nisha has glued 27 small cubes together to make a large solid cube. She paints the large cube red. How many of the original small cubes have—
(a) three faces painted red?
(b) two faces painted red?
(c) one face painted red?
(d) no faces painted red?
Ans:
Nisha has a large solid cube made from 27 small cubes. Since 3 × 3 × 3 = 27, the large cube is a 3 × 3 × 3 cube.
She paints the entire large cube red.
(a) The large solid cube has 8 corner cubes, and each corner small cube is painted red.
So, 8 small cubes are three faces painted red.
(b) Since a cube has 12 edges or sides, and 1 cube in the middle of each edge is painted red.
So, there are 12 small cubes with two faces painted red.
(c) These are the small cubes located in the center of each face of the large cube. A cube has 6 faces. Each face of the large cube is a 3 × 3 square of small cubes. The center small cube of each 3 × 3 face has only one face exposed to the outside, or painted red. So, there are 6 small cubes with one face red.
(d) For a 3 × 3 × 3 = 27 cube, if we remove the outer layer of cubes, we are left with an inner cube. This means there is only 1 small cube right in the very center of the large cube that has no faces painted red.
Puzzle
Tanu arranged 7 shapes in a line. She used 2 squares, 2 triangles, 1 circle, 1 hexagon, and 1 rectangle.
Find her arrangement using the following clues:
(a) The square is between the circle and the rectangle.
(b) The rectangle is between the square and the triangle.
(c) The two triangles are next to the square.
(d) The hexagon is to the right of the triangle
(e) The circle is to the left of the square.
Ans: The arrangement is: Triangle, Circle, Square, Rectangle, Triangle, Hexagon, Square.
Page No. 103
Icosahedron and Dodecahedron
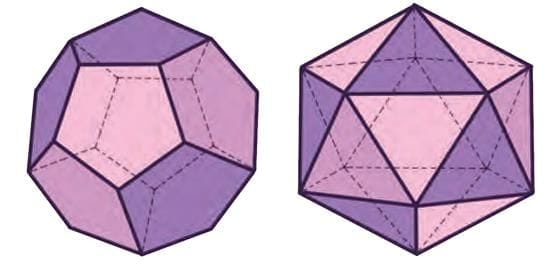
Q: What do these names mean? Once you count their faces, you will know.
Ans: Icosahedron: It is a geometric solid with 20 faces, typically shaped as equilateral triangles in the case of a regular icosahedron.
Dodecahedron: It is a three-dimensional shape having twelve plane faces, in particular a regular solid figure with twelve equal pentagonal faces.
Q: What shapes do you see in an icosahedron and a dodecahedron?
Ans:
Icosahedron: Equilateral triangles, Dodecahedron: Regular pentagons
Q: Do all the faces look the same?
Ans:
Icosahedron: Yes, Dodecahedron: Yes
Q: How many faces meet at a vertex (point)?
Ans:
Icosahedron: 5 faces (Equilateral triangles), Dodecahedron: 3 faces (Regular pentagons)
Q: Do the same number of faces meet at each vertex?
Ans:
Icosahedron: Yes, Dodecahedron: Yes
Q: How many edges do you see?
Ans: The edge is the line where two faces meet.
Icosahedron: It has 30 edges.
Dodecahedron: It has 30 edges.
Q: How did you count them such that you do not miss out any edge or count an edge twice?
Ans: For the Icosahedron: We can see that each of the 20 triangles has 3 sides,
so 20 x 3 = 60.
But each edge is shared by 2 triangles. So, we counted every edge twice. The real number is 60 ÷ 2 = 30 edges.
For the Dodecahedron: Each of the 12 pentagons has 5 sides,
so 12 x 5 = 60.
Again, each edge is shared by 2 pentagons.
So, 60 ÷ 2 = 30 edges.
Q: Can you think of any other solid shapes that have faces that look the same?
Ans:
Yes, there are a few other types of shapes where all faces are identical. These are known as platonic solids. Besides the icosahedron and dodecahedron, the other platonic solids are:
- Tetrahedron: 4 faces, all are equilateral triangles.
- Cube: 6 faces, all are squares.
- Octahedron: 8 faces, all are equilateral triangles.
Do the same number of faces meet at each common vertex?
Ans: Yes.
You can also build some 3-D shapes using straws or ice-cream sticks and clay or play dough. Which shapes did you make?
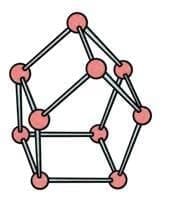
Ans: With straws and clay, we can make:
Cubes and cuboids (like a box).
Pyramids with a square base (square pyramid) or a triangular base (tetrahedron).
Triangular prisms (like a tent shape).
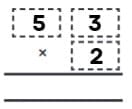

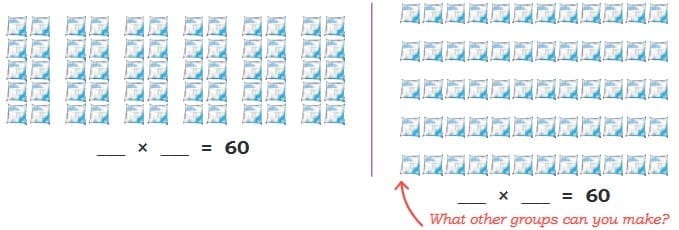
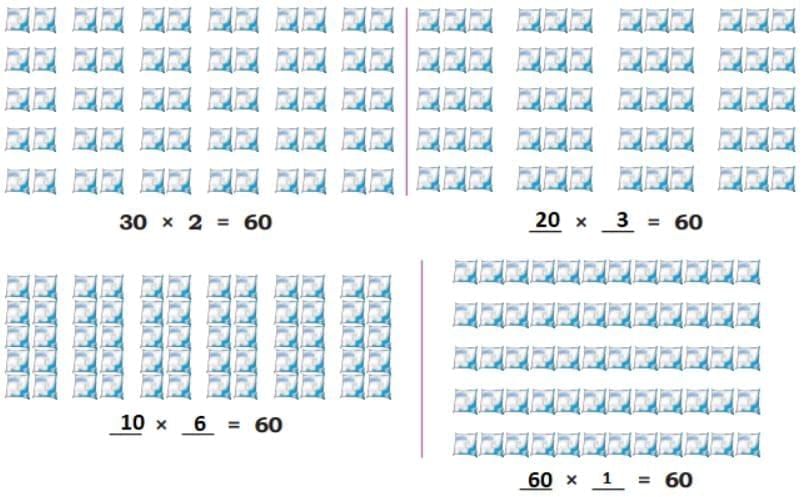


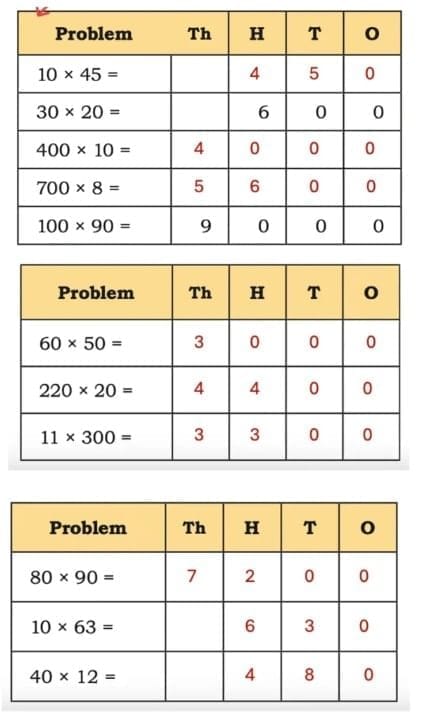
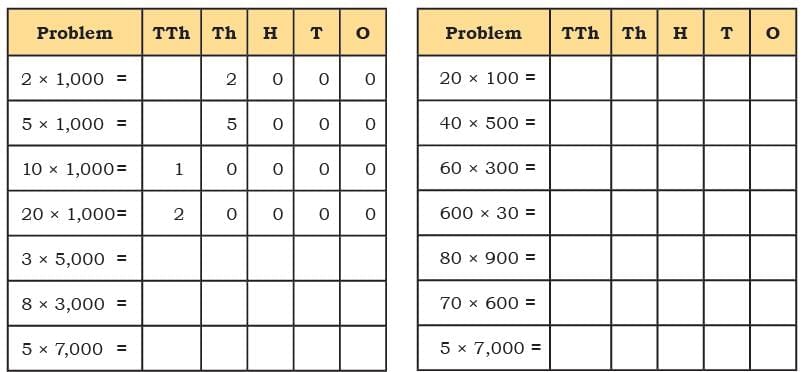
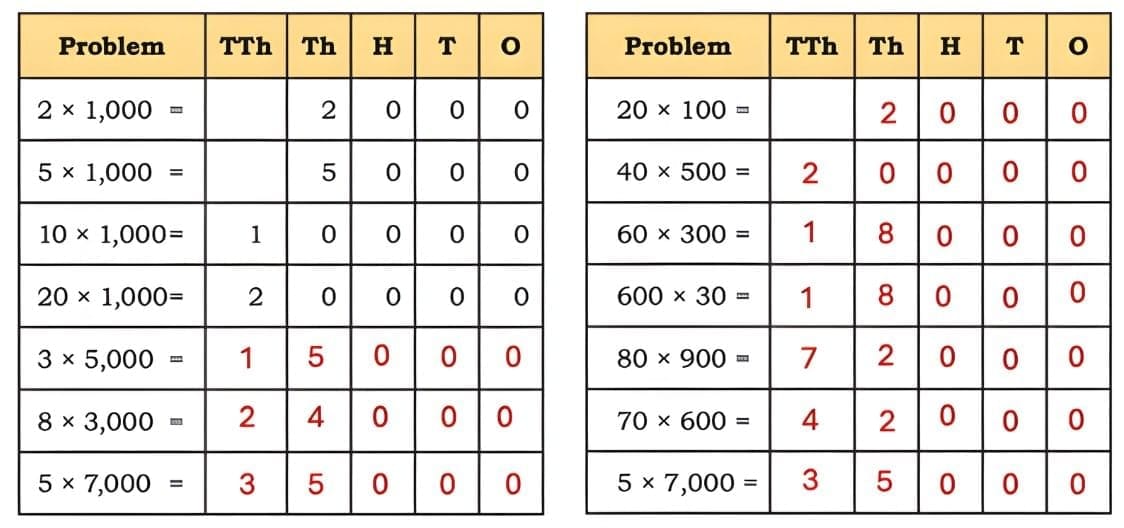
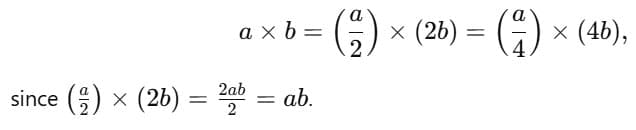


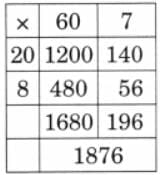
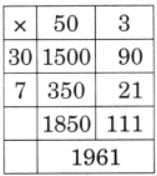
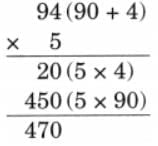

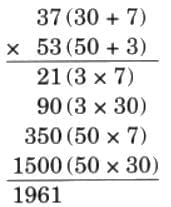

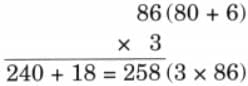
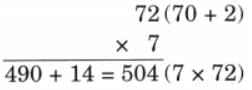

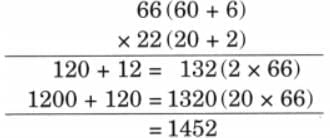

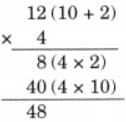
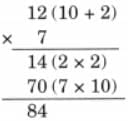
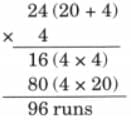
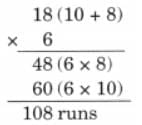
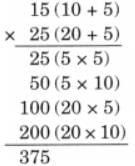
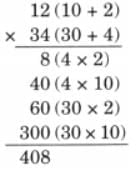

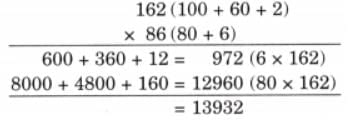
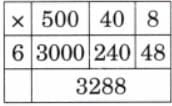
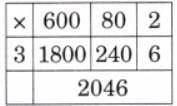
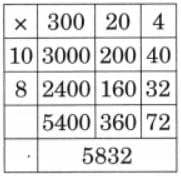
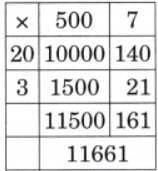
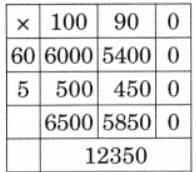

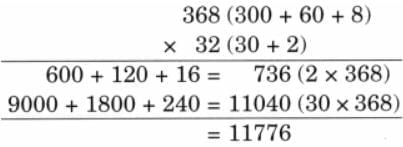

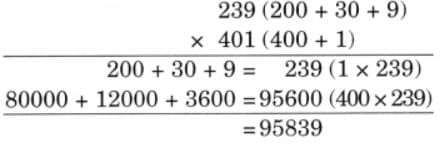
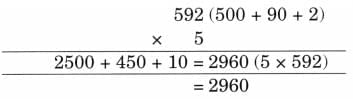
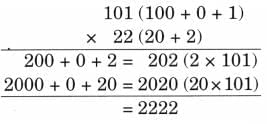
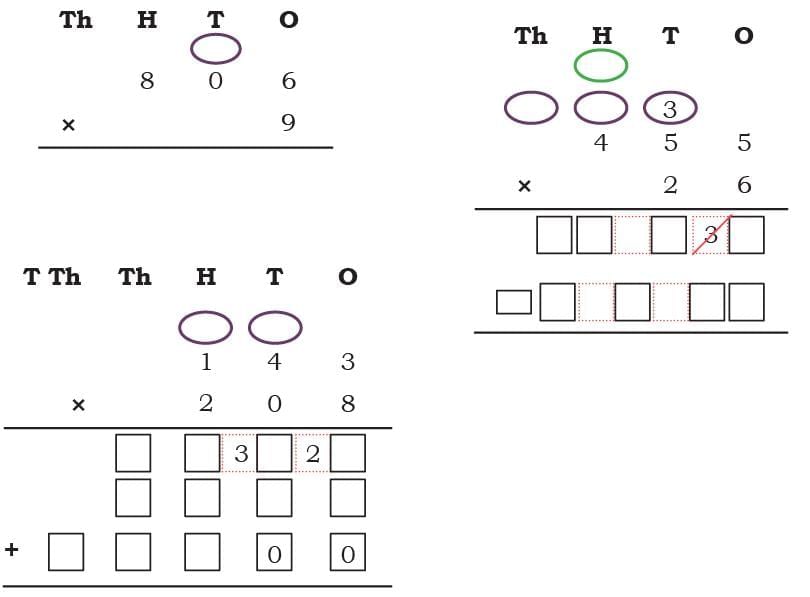
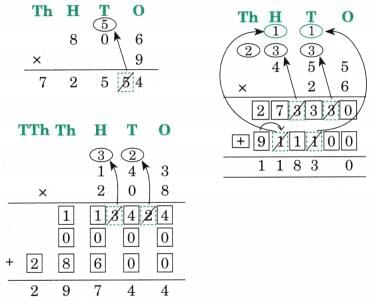
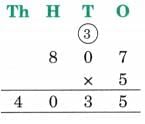

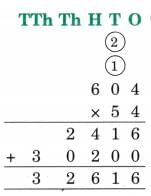
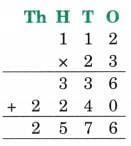
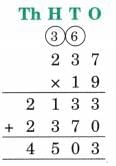


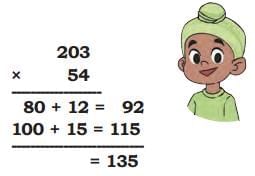

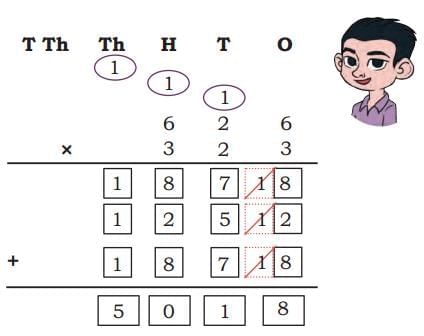




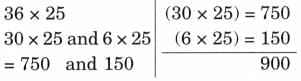
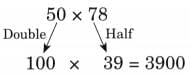
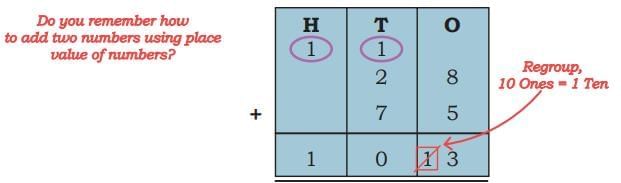
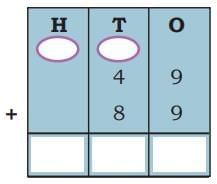
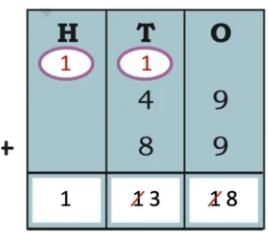
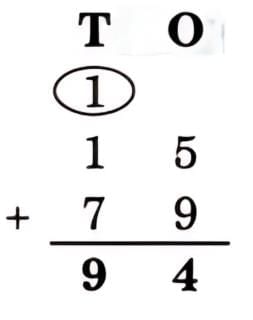
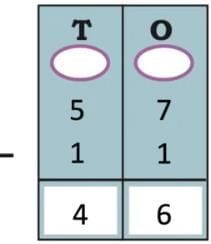
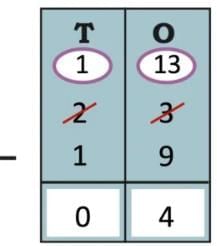
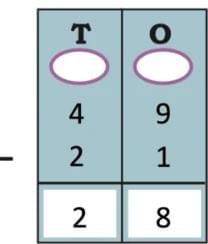
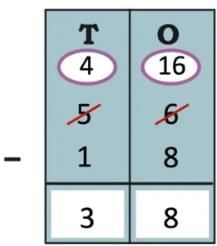

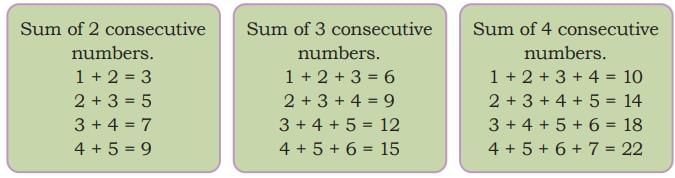
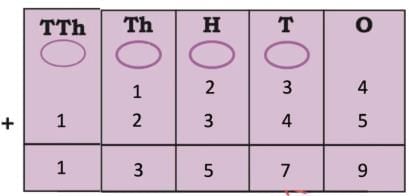
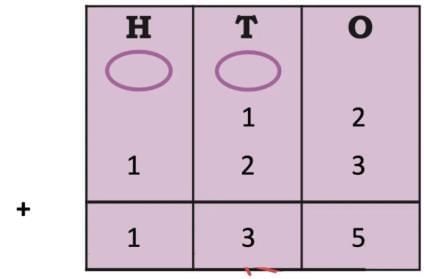
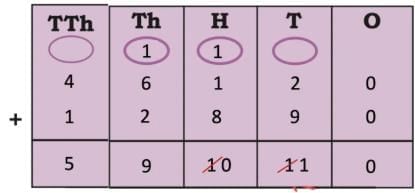
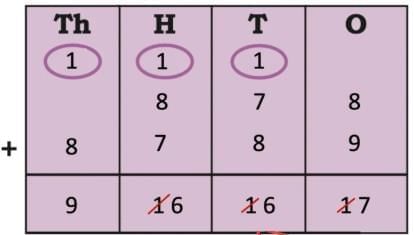
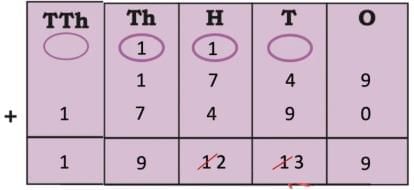

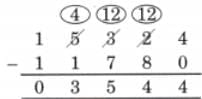
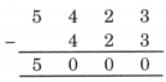


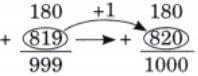
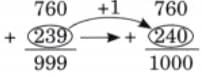
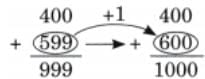
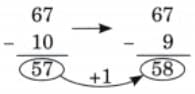
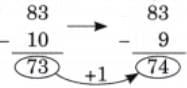
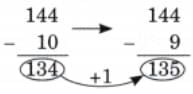
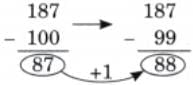
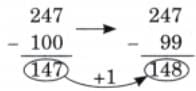
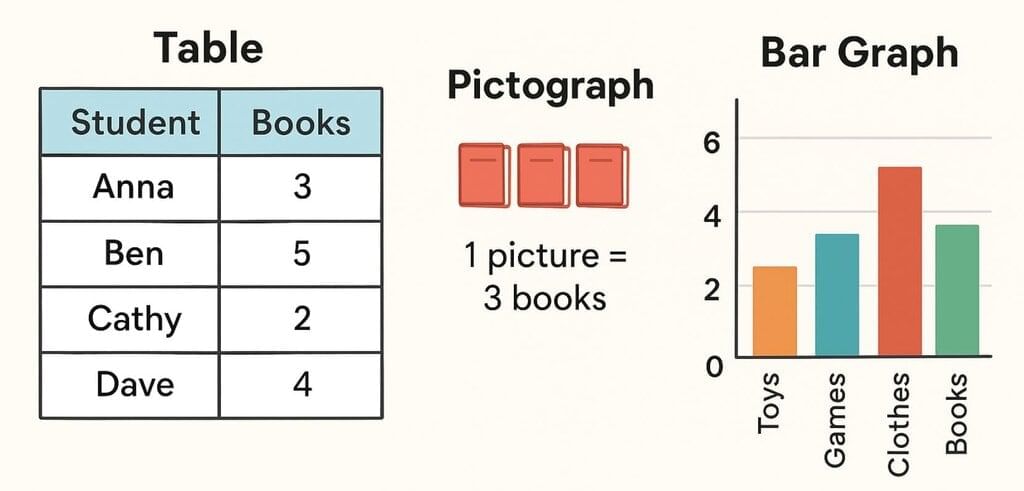
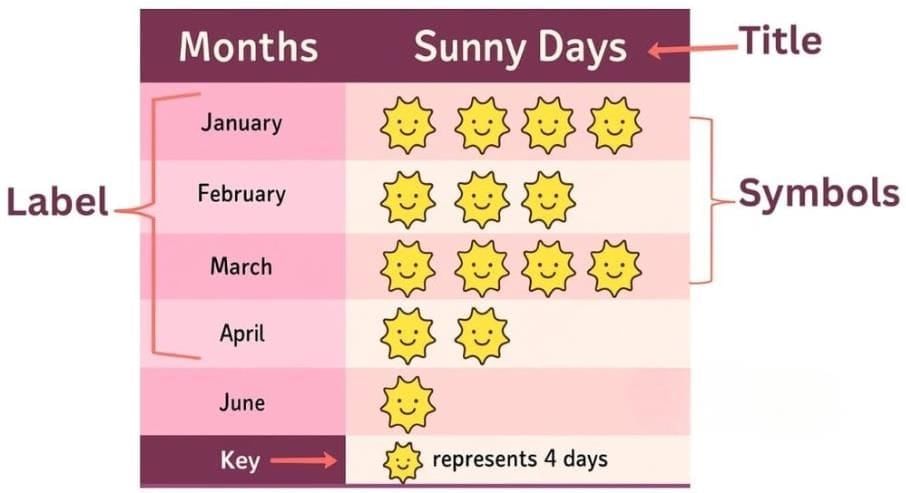
 The collected data was organised in a table, which shows how much time each child spends watching TV.
The collected data was organised in a table, which shows how much time each child spends watching TV. 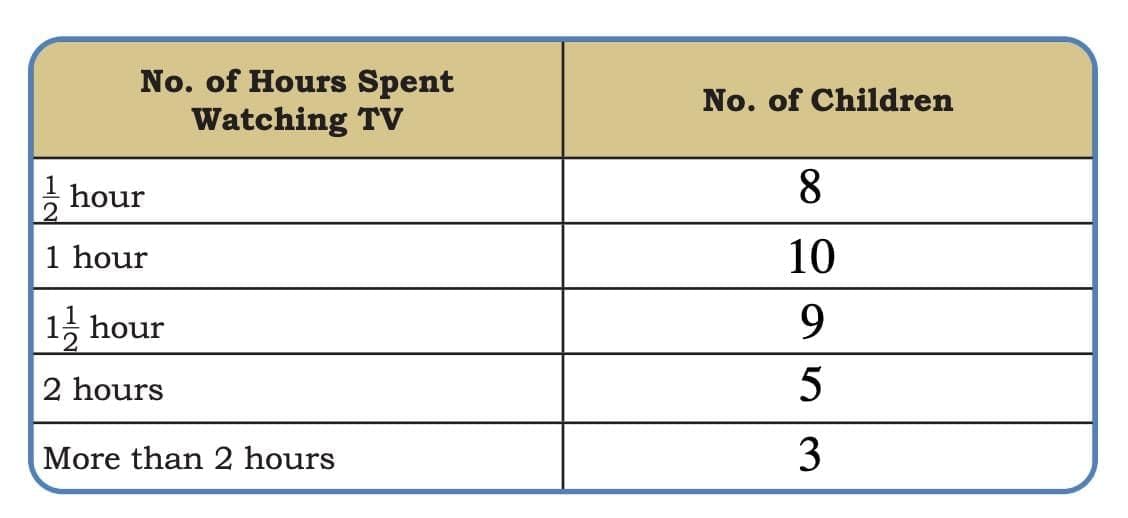 Based on this information, we will answer a few questions related to their TV viewing habits.
Based on this information, we will answer a few questions related to their TV viewing habits.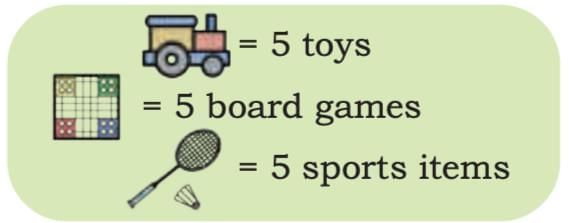
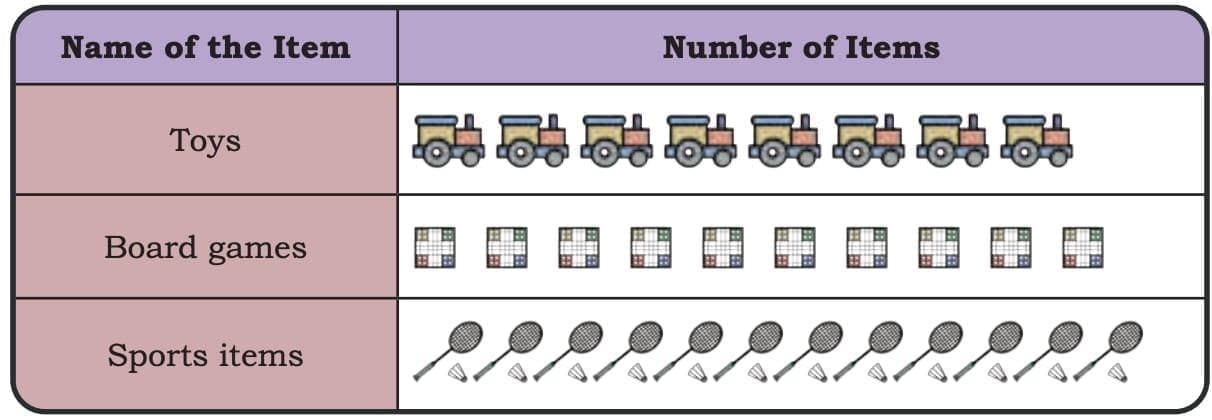
 Observe the pictograph and answer the following questions.
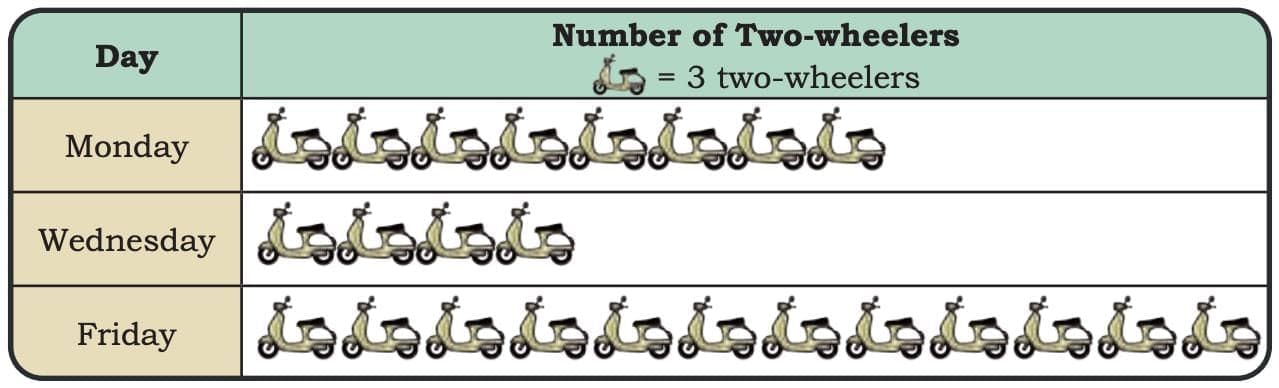
Observe the pictograph and answer the following questions.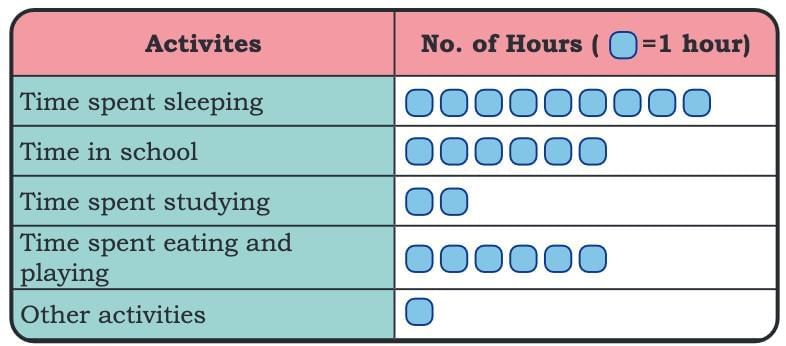 Sheela recorded her routine in the following manner:
Sheela recorded her routine in the following manner: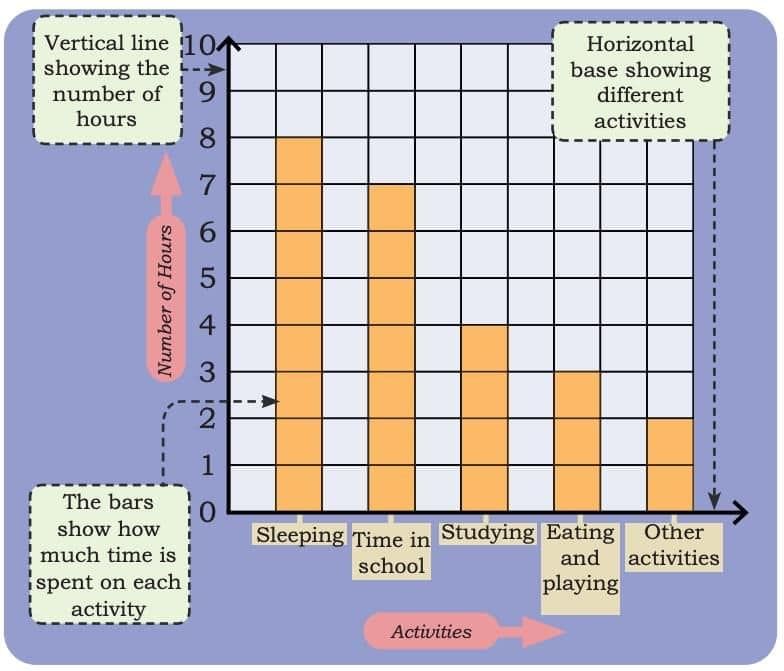 How is Sheela’s recording different from Raman’s recording?
How is Sheela’s recording different from Raman’s recording?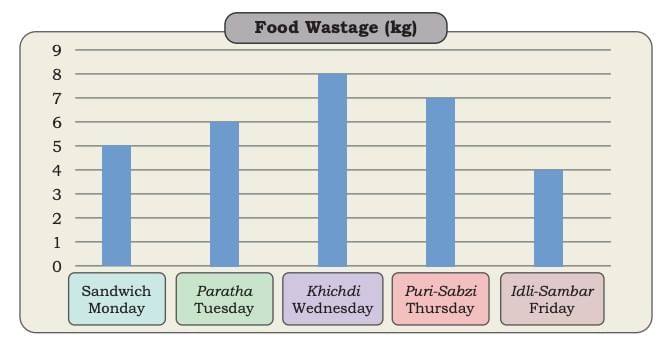 Rani was shocked to see the data. What do you think about food wastage? How can we reduce the wastage of food? What can we do with the leftover food?
Rani was shocked to see the data. What do you think about food wastage? How can we reduce the wastage of food? What can we do with the leftover food?